基于可变拟阵搜索算法构造码率为1/p的二进制系统准循环码
2016-10-13张水平林平平巫光福江林伟
张水平 林平平 巫光福 江林伟
基于可变拟阵搜索算法构造码率为1/的二进制系统准循环码
张水平 林平平 巫光福*江林伟
(江西理工大学信息工程学院 赣州 341000)
该文针对拟阵搜索算法复杂度高以及局部拟阵搜索算法无法搜索到全部最优码的问题,通过研究拟阵搜索算法,提出可变拟阵搜索算法,并用于搜索准循环码。该算法通过减少重复搜索从而降低运算复杂度;基于该算法构造码率为1/的二进制系统准循环码,随着整数的变化,生成矩阵减少或者增加一个循环矩阵,产生码率均为1/的最优码。通过实验得到两个最小距离比现有最优码更大的准循环码,表明算法的可行性和优越性。
拟阵理论;准循环码;最小距离;可变拟阵搜索算法
1 引言
1967年,Townsend和Weldon[1]发现准循环码,二进制系统准循环码由于循环性、电路实现简单、良好的代数结构和纠错能力,受到广大研究学者的关注,并取得许多研究成果。提出计算机组合优化搜索算法[2]、局部搜索算法[3]、等差数列算法[4]搜索最优码,许多性能良好的准循环码被收集在数据库[5]。文献[6,7]研究准循环码在无线传感器网络和浅海水声信道中的应用,文献[8]对其译码器电路实现进行相关研究,使得准循环码在实际环境中得到广泛应用。
拟阵理论与编码的结合,指明准循环码研究的新方向。1935年,Whitney[9]提出拟阵理论。之后,文献[10]第1次把拟阵与编码结合起来,推导出著名的MacWilliams等式。1997年,文献[11]得到更一般化的汉明重量分布的MacWilliams等式。2008年,文献[12]系统地把拟阵引入编码中,指出二进制码可以对应于二进制的向量拟阵;反之,二进制向量拟阵也对应于二进制码。在此基础上,文献[13]基于拟阵理论构造一种短的高码率LDPC码,表明拟阵理论用于编码领域的可行性和高效性。最近,文献[14]基于拟阵理论,根据生成矩阵和最小距离的联系,发现构造二进制线性码的最小距离定理,提出拟阵搜索算法,构造一类好的二进制系统线性分组码。文献[15]进一步探究生成矩阵和最小距离的联系,发现构造二进制准循环码的最小距离定理,提出拟阵搜索算法,构造码率为1/的二进制系统准循环码。拟阵搜索算法可以降低运算的复杂度,能搜索更大的最优码,且属于全局搜索,能够保证最优码。但只能构造14的二进制系统准循环码,之后因运算量大无法继续搜索。为了克服这种局限性,文献[16]提出局部拟阵搜索算法,构造15的码率为1/的二进制系统准循环码,通过实验得到20多个最优码。该算法可以搜索15的准循环码,但无法保证最优码。基于拟阵理论构造二进制系统准循环码,因运算量大产生的局限性,无法继续搜索,更大的最优码。
本文在拟阵搜索算法的基础上,提出可变拟阵搜索算法。首先利用拟阵搜索算法构造高码率最优码,输出所有生成矩阵到文本;然后对每个生产矩阵,遍历二进制准循环码的子集,组合低码率的生产矩阵,结合二进制准循环码的关系矩阵,通过拟阵搜索算法求得最小距离;最后比较所有最小距离,得到低码率最优码,将所有最优码的生产矩阵输出到文本。为了构造更低码率的最优码,重复上述步骤,直到满足码率即可。该算法既可搜索15的准循环码,降低运算的复杂度,又可搜索最优码。基于该算法构造=12~18,=20,二进制系统准循环码,实验结果得到两个最小距离比现有最优码更大的准循环码,同时具有码率可变性。
2 可变拟阵搜索算法
2.1算法分析
拟阵理论经过许多学者的研究,已经得到充分的发展和应用,拟阵理论已被广泛用于组合优化、网络理论和编码理论,Oxley在文献[17]中详细阐述了拟阵的定义和定理。拟阵与编码之间的联系,最重要在于构造与二进制线性分组码相对应的向量拟阵,通过向量拟阵的性质,得到生成矩阵与最小距离的联系,降低求解最小距离的复杂度。文献[14]提出拟阵联接度的定义,通过建立一系列拟阵与单个集合的关系,重新定义新的拟阵独立性,发现基于拟阵理论构造二进制线性分组码的最小距离定理,提出拟阵搜索算法,基于该算法构造二进制线性分组码。文献[15]将拟阵理论用于构造准循环码,将分解为子集的集合,每个子集中的元素个数作为向量的元素,,序号作为向量的元素。根据子集与拟阵的基的交集个数,得到二进制线性分组码的关系矩阵。构造准循环码,中元素个数必须等于,组成序号集合,根据得到准循环码的关系矩阵,发现基于拟阵理论构造准循环码的最小距离定理,提出构造准循环码的拟阵搜索算法。该算法是一种全局遍历算法,当,已知时,复杂度为,大于14时,由于拟阵数量过多,导致处理的数据量非常大,无法继续进行搜索。文献[16]通过随机产生向量,利用拟阵理论构造准循环码的最小距离定理,提出局部拟阵搜索算法,搜索大于14的最优码。该算法搜索最优码具有随机性,无法保证最优码。当搜索更大的最优码时,处理的数据量亦非常大。
当搜索码率为1/的二进制系统准循环码,拟阵搜索算法和局部拟阵搜索算法需要对个循环矩阵进行遍历,局部拟阵搜索算法非全局搜索,次数较少。搜索码率为1/(+1)的二进制系统准循环码时,生成矩阵和前个循环矩阵可能相同,且都能构造最优码。如果基于生成矩阵,对第(+1)个循环矩阵遍历,寻找最优码,既能减少重复搜索,降低复杂度,还可得到最优码。基于此思想,本文提出可变拟阵搜索算法,构造码率为1/的二进制系统准循环码,只对第个循环矩阵遍历,前个循环矩阵为生成矩阵,生成矩阵能构造最优码。可变拟阵搜索算法,上一步的输出是下一步的输入,对上一步的输出进行搜索遍历,求解最小距离,寻找最优码,将结果输出到文本。搜索最优码是一个循序渐进过程,首先读取所有最优码的生成矩阵,利用拟阵搜索算法遍历循环矩阵,组合生成矩阵,求解最小距离,寻找最优码,然后将最优码的生成矩阵输出到文本。然后重复上述操作,直到满足需要的值。
例如当= 14,已知码率为1/5的二进制系统准循环最优码的生成矩阵为,为了构造码率为1/4的二进制系统准循环最优码,只需把中的循环矩阵删除,得。为了构造码率为1/6的二进制系统准循环最优码,只需在生成矩阵末端加上循环矩阵,得到,然后进行拟阵搜索算法遍历,得到合适的循环矩阵。
2.2算法设计
首先,利用构造准循环码的拟阵搜索算法,构造码率为1/2的系统准循环码。即先将分解成子集的集合,筛选满足条件的,得到序号集合,求解与构造准循环码有关的关系矩阵。根据基于拟阵理论构造准循环码的最小距离定理,寻找最优码,将最优码的所有生成矩阵输出到文本。假设生成矩阵,,,,,根据最小距离定理,,,,因为构造系统码,所以。如果是生成矩阵的一部分,则,,否则。根据生成矩阵可知。为了得到最小距离,根据最小距离定理,求得。是一个的矩阵,是一个的矩阵,可知是一个的矩阵。与其它拟阵的联系度为一个行向量,因此生成矩阵的对应中的某一行,同时决定中对应位置元素的取值,根据矩阵相乘原理,中的对应中的所有行向量相加得到。码的最小距离,为了得到更大的,所以只要得到更小的,同时因为=,因此码的最小距离
最后,根据码率为1/的所有系统准循环码的生成矩阵,按照构造码率为1/3的准循环码步骤,构造码率为1/(+1)的系统准循环码,直到满足给定的参数。生成矩阵首先是码率为1/(+1)的生成矩阵前个循环矩阵,然后遍历所有的循环矩阵,得到最后一个循环矩阵,组成生成矩阵。根据最小距离定理求得最小距离,如果是满足这一特性的最大值,则是码率的生成矩阵前个循环矩阵,且和组成生成矩阵,否则不是。可变搜索算法是在生成矩阵的基础上进行的拟阵搜索算法,构造准循环码是一个循环渐进过程。
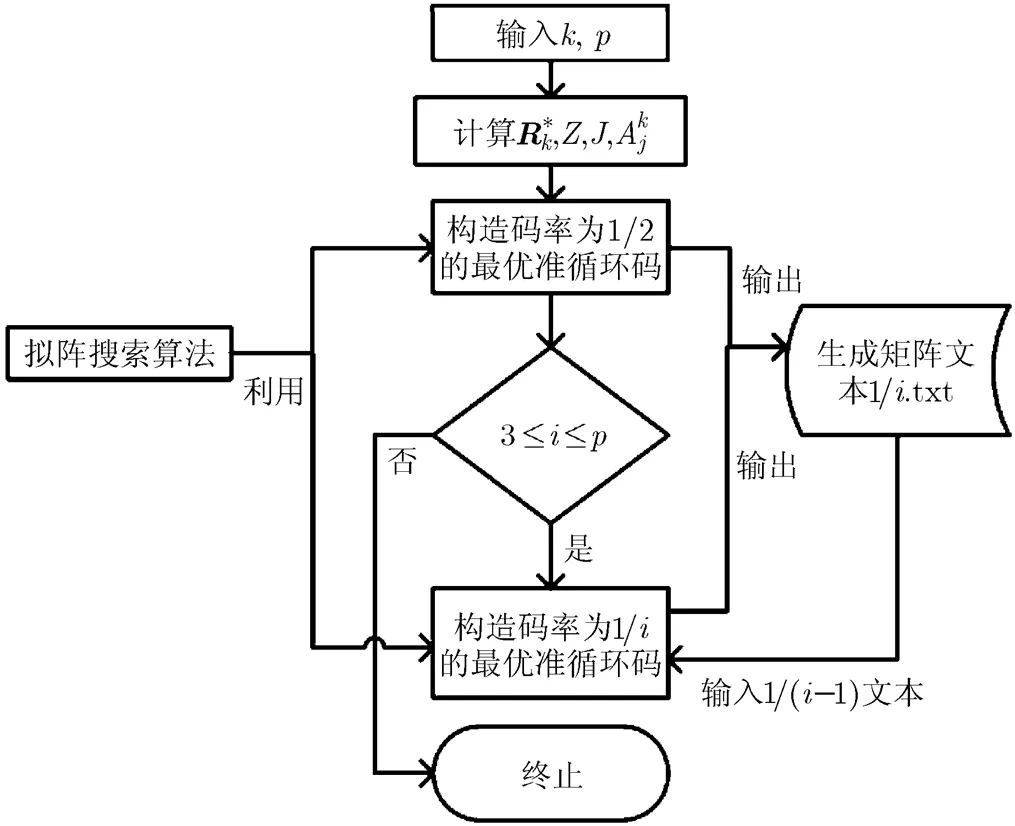
图1 可变拟阵搜索算法流程图
可变拟阵搜索算法,上一步的输出是下一步的输入,在前面基础上进行的拟阵搜索,构造准循环码是一个循序渐进过程。首先构造=2的满足这一特性的准循环码,得到与之相对应的所有生成矩阵,然后通过程序读取这些生成矩阵,对每个生成矩阵进行拟阵搜索算法遍历,构造= 3的准循环码,寻找最大的最小距离。构造更大的准循环码时,重复上述步骤,直到构造满足要求的准循环码。即首先构造高码率的二进制系统循环码,然后在上一步输出的基础上构造较低码率的二进制系统准循环码,追求码率可变和最小距离的最大值。当已知,时,复杂度为,其中是码率为1/(-1)的最优码生成矩阵的个数,而是关系矩阵的行数,都是常数。拟阵搜索算法的复杂度为,局部搜索算法的复杂度为,显然可变拟阵搜索算法的复杂度更低。该算法通过减少重复搜索降低复杂度,可以搜索更长的码字,寻找最优码。美中不足的是,当已知,时,前面高码率最优码的生成矩阵必须全部求解出来,利用已知高码率最优码搜索低码率最优码。拟阵搜索算法和局部拟阵搜索算法跟前面高码率最优码的生成矩阵没有联系,可以直接求解。
可变拟阵搜索算法步骤(如图1所示):
(1)给定两个参数和,计算关系矩阵,,,。
(3)读取码率为1/的二进制系统准循环码的所有生成矩阵,利用步骤(2)中的拟阵搜索算法思想计算最小距离,构造码率为1/(+1)的最优系统准循环码。
例如,当=4,=2时,,,即满足的子集有,,,与准循环码有关的关系矩阵:
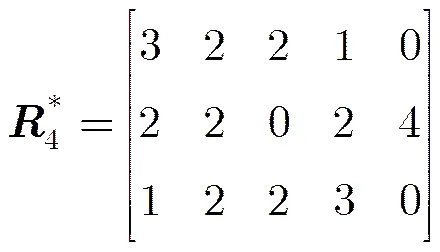
首先构造码率为1/2的二进制系统准循环最优码,其结果唯一,生产矩阵为,最小距离=4。现在需要构造码率为1/3的二进制系统准循环最优码,只需在生成矩阵的末端加上循环矩阵,根据码率可变拟阵搜索算法,循环矩阵有3种情况,我们对其进行拟阵搜索算法遍历,找到最优码。
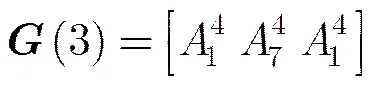
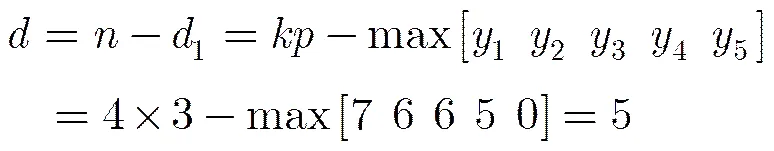
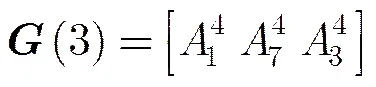
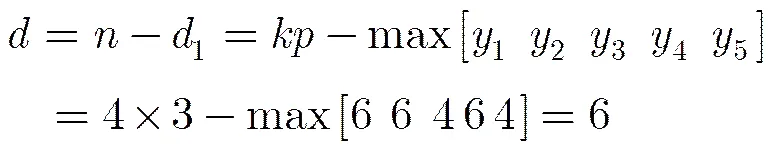
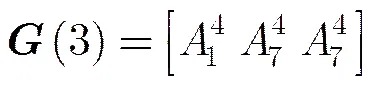
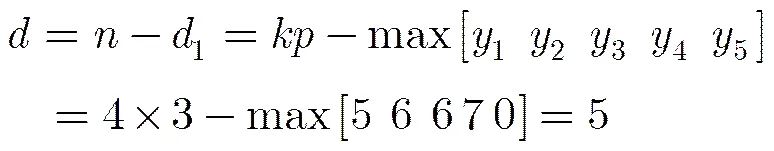
通过码率可变拟阵搜索算法,我们得到码率为1/3的最优系统准循环码生成矩阵为。当已知码率为1/3的最优系统准循环码的生成矩阵为,我们可知满足这一特性的码率为1/2的最优系统准循环码的生成矩阵为,最小距离= 4。如果需要构造码率为1/4的最优系统准循环码,在生成矩阵的基础上进行码率可变拟阵搜索算法即可。
3 实验结果
基于可变拟阵搜索码算法,构造一类特殊码率为1/的二进制系统准循环码,具备码率可变性,伴随着的变化,生成矩阵减少或者增加一个循环矩阵,产生码率均为1/的最优码。本文所指得最优码,是满足这一特性的生成矩阵所能得到的最大的最小距离,并非广义上的最优码。通过对比文献[16,19]和两个数据库[5,20],得到最小距离见表1。其中,粗体的最小距离和现有最优准循环码的最小距离相同,粗体加*号的最小距离比现有最优准循环码的最小距离大, 即码(182, 14, 77)和(340, 17, 146)。
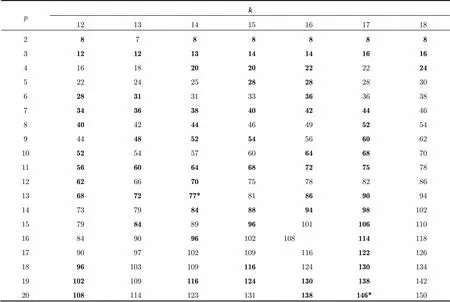
表1 (kp, p)码的最小距离
表2中列出码率为1/20即=20的最优码的生成矩阵代表,根据准循环码的定义以及可变拟阵搜索算法,验证码率可变性,随着的变化,生成矩阵增加或者减少一个循环矩阵,产生均为最优码。例(240, 12, 108)码生成矩阵=[1 379 29 311 749 137 447 989 1371 199 661 35 53 861 893 73 83 235 349 663],根据准循环码的定义,其中“1”表示12×12循环矩阵,首列为[1 0 0 0 0 0 0 0 0 0 0 0]T,其他数字同样表示循环矩阵,首列为其二进制表示,因此是由20个循环矩阵组成的12×240生成矩阵。根据可变拟阵搜索算法,在码率为1/的生成矩阵上增加一个循环矩阵,组成码率为生成矩阵,两个生成矩阵产生的均为最优码。所以减少“663”表示的循环矩阵,由=[ 1 379 29 311 749 137 447 989 1371 199 661 35 53 861 893 73 83 235 349]亦产生最优码。根据表1可知,它是(228, 12, 102)码,增加一个循环矩阵亦是如此。从表2可知= 20的最优准循环码的生成矩阵,亦知的最优准循环码的生成矩阵,即=[1 379],以此类推。根据= 20的最优码生成矩阵可以构造= 21的最优码,以此类推,得到更大的最优码。
码的重量分布定义为:设为上的线性码,分别为中重量为0,1,,码字的个数,为的重量分布,设,为变元,称次齐次多项式为的重量计算子。根据二进制线性码最小距离定义,等于非零码字的最小重量,而表示线性码重量为的码字个数,因此根据最优码的重量分布可以验证表1的最小距离。查看(240, 12, 108)码的重量分布可知,非零码字的最小重量的数量为,因此最小距离= 108,符合表1列出的数值。根据表2中的生成矩阵代表亦可验证表1的最小距离。二进制线性码表示成向量形式为=,由于本文构造的是系统码,而系统码具有前位是信息位的特点,因此码的重量为wt()=wt()+ wt(),其中是生成矩阵删除单位矩阵后的矩阵。例,(240, 12, 108)码的生成矩阵=[ 1 379 29 311 749 137 447 989 1371 199 661 35 53 861 893 73 83 235 349 663],可以验证=12,=2~20时准循环码的最小距离。当= 12,= 2时,=[1 379],“1”,“379”表示12×12循环矩阵,首列为[1 0 0 0 0 0 0 0 0 0 0 0]T和[1 1 0 1 1 1 1 0 1 0 0 0]T,是“379”表示的循环矩阵。根据wt()=wt()+ wt(),求得重量计算子为,非零码字的最小重量的数量为,因此= 8,符合表1中当= 12,= 2时的最小距离。
上标代表重量,下标代表数量,则由表2中生成矩阵生成的最优码重量分布如下:
(1)新准循环码(340,17,146)的重量分布为:
10, 272146, 867148, 1258150, 2091152, 2941154, 3723156, 4743158, 6171160, 7259162, 8942164, 10370166, 10421168, 11408170, 11526172, 10778174, 9367176, 8007178, 6290180, 4335182, 3485184, 2380186, 1530188, 1377190, 748192, 323194, 289196, 51198, 51200, 17202, 17204, 17208, 17210。
(2)新准循环码(182,14,77)的重量分布为:
10, 28277, 25278, 39280, 67281, 43482, 63084, 135885, 65886, 82688, 182089, 88290, 84092, 87594, 74996, 124697, 63098, 518100, 574101, 294102, 98104, 280105, 70106, 28108, 70109, 14112, 14113, 1126。
4 结束语
本文主要研究如何利用拟阵理论构造二进制系统准循环码,搜索,更大的最优码。在基于拟阵理论的拟阵搜索算法和局部拟阵搜索算法的基础上,提出可变的拟阵搜索算法。该算法可搜索15的准循环码,减少重复搜索,降低运算复杂度,亦可得到最优码。算法构造一类特殊的码率为1/的二进制系统准循环码,该码有码率可变性。实验结果相比现有的最优准循环码,大部分最小距离与现有最优码的最小距离相差不大,多数与现有最优码的最小距离相等,关键得到两个准循环码(182, 14, 77)和(340, 17, 146)比现有的准循环码的最小距离更大。算法特点和实验结果表明算法的可行性和优越性。实际通信系统中,在保证良好纠错能力的前提下,采用本文所构造的编码,生成矩阵减少或者增加循环矩阵即可满足变换码率的需求,操作方便,具有一定的应用价值。
表2码率可变的最优码
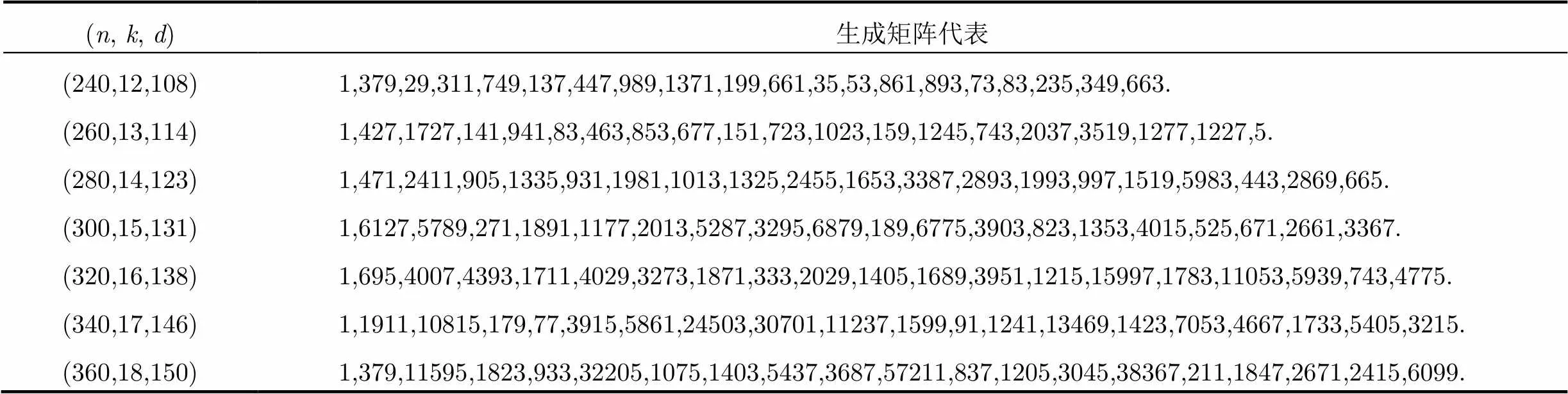
(n, k, d)生成矩阵代表 (240,12,108)1,379,29,311,749,137,447,989,1371,199,661,35,53,861,893,73,83,235,349,663. (260,13,114)1,427,1727,141,941,83,463,853,677,151,723,1023,159,1245,743,2037,3519,1277,1227,5. (280,14,123)1,471,2411,905,1335,931,1981,1013,1325,2455,1653,3387,2893,1993,997,1519,5983,443,2869,665. (300,15,131)1,6127,5789,271,1891,1177,2013,5287,3295,6879,189,6775,3903,823,1353,4015,525,671,2661,3367. (320,16,138)1,695,4007,4393,1711,4029,3273,1871,333,2029,1405,1689,3951,1215,15997,1783,11053,5939,743,4775. (340,17,146)1,1911,10815,179,77,3915,5861,24503,30701,11237,1599,91,1241,13469,1423,7053,4667,1733,5405,3215. (360,18,150)1,379,11595,1823,933,32205,1075,1403,5437,3687,57211,837,1205,3045,38367,211,1847,2671,2415,6099.
[1] TOWNSEND R and WELDON E. Self-orthogonal quasi-cyclic codes[J]., 1967, 13(2): 183-195.doi: 10.1109/TIT.1967. 1053974.
[2] CHEN Z. New results on binary quasi-cyclic codes[C]. Proceedings of IEEE International Symposium on Information Theory, Sorrento Italy, 2000: 151-154.
[3] HEIJNEN P, VAN T H, VERHOEFF T,. Some new binary quasi-cyclic codes[J]., 1998, 44(5): 1994-1996.doi: 10.1109/ 18.705580.
[4] 张轶, 达新宇, 苏一栋. 利用等差数列构造大围长准循环低密度奇偶校验码[J]. 电子与信息学报, 2015, 37(2): 394-398. doi: 10.11999/JEIT140538.
ZHANG Yi, DA Xinyu, and SU Yidong. Construction of quasi-cyclic low-density parity-check codes with a large girth based on arithmetic progression[J].&, 2015, 37(2): 394-398. doi: 10.11999/JEIT140538.
[5] CHEN Z. Database of quasi-twisted codes[OL]. http:// moodle. tec.hkr.se/~chen/research/codes, 2015.9.
[6] 郭锐, 刘春于, 张华, 等. 分簇无线传感器网络中根校验全分集LDPC码设计与能效分析[J]. 电子与信息学报, 2015, 37(7): 1580-1585. doi: 10.11999/JEIT141294.
GUO Rui, LIU Chunyu, ZHANG Hua,. Full diversity LDPC codes design and energy efficiency analysis for clustering wireless sensor networks[J].&, 2015, 37(7): 1580-1585. doi: 10.11999/JEIT141294.
[7] 陈震华, 许肖梅, 陈友淦, 等. 浅海水声信道中原模图LDPC码的设计及性能分析[J]. 电子与信息学报, 2016, 38(1): 153-159. doi:10.11999/JEIT150415.
CHEN Zhenhua, XU Xiaomei, CHEN Yougan,. Design and analysis of Protograph-based LDPC codes in shallow water acoustic channels[J].&, 2016, 38(1): 153-159. doi: 10.11999/ JEIT150415.
[8] 兰亚柱, 杨海钢, 林郁. 动态自适应低密度奇偶校验码译码器的FPGA实现[J]. 电子与信息学报, 2015, 37(8): 1937-1943. doi: 10.11999/JEIT141609.
LAN Yazhu, YANG Haigang, and LIN Yu. Design of dynamic adaptive LDPC decoder based on FPGA[J].&, 2015, 37(8): 1937-1943. doi: 10.11999/JEIT141609.
[9] WHITNEY H. On the abstract properties of linear dependence[J]., 1935, 57(1): 509-533. doi: 10.1007/978-1-4612-2972-8_10.
[10] GREENE C. Weight enumeration and the geometry of linear codes[J]., 1976, 55(55): 119-128. doi: 10.1002/sapm1976552119.
[11] BARG A. The matroid of supports of a linear code[J].&, 1997, 8(2): 165-172. doi: 10.1007/s 002000050060.
[12] KASHYAP N. A decomposition theory for binary linear codes[J]., 2008, 54(7): 3035-3058.doi: 10.1109/TIT.2008.924700.
[13] 巫光福, 王琳. 一种短的高码率LDPC码设计[J].应用科学学报, 2013, 31(6): 559-563. doi: 10.3969/j.issn.0255-8297. 2013.06.002.
WU Guangfu and WANG Lin.Design of a short high rate LDPCcode[J]., 2013, 31(6): 559-563. doi: 10.3969/j.issn.0255-8297.2013.06.002.
[14] WU Guangfu, WANG Lin, and TRUONG T K. Use of matroid theory to construct a class of good binary linear codes[J]., 2014, 8(6): 893-898. doi: 10.1049/iet-com.2013.0671.
[15] WU Guangfu, Chang H C, WANG Lin,. Constructing rate 1/p systematic binary quasi-cyclic codes based on the matroid theory[J]., 2014, 71(1): 47-56. doi: 10.1007/s10623-012-9715-1.
[16] WU Guangfu, LI Yong, ZHANG Shuiping,. A random local matroid search algorithm to construct good rate 1/systematic binary Quasi-Cyclic codes[J]., 2015, 19(5): 699-702.doi: 10.1109/ LCOMM.2015.2401572.
[17] OXLEY J. Matroid Theory [M]. Oxford U K, Oxford University Press, 2011: 5-26.
[18] TILBURG H C A V. On quasi-cyclic codes with rate 1/[J]., 1978, 24(5): 628-629.doi: 10.1109/TIT.1978.1055929.
[19] GULLIVER T A and BHARGAVA V K. An updated table of rate 1/binaryuasi-yclic codes[J]., 1995, 8(5): 81-86. doi: 10.1016/0893-9659 (95)00071-W.
[20] GRASSL M. Tables of linear codes and quantum codes [OL]. http://www.codetables.de, 2015.9.
Construct the Systematic Binary Quasi-cyclic Codes with Rate 1/ased on Variable Matroid Search Algorithm
ZHANG Shuiping LIN Pingping WU Guangfu JIANG Linwei
(,,341000,)
Because the matroid search algorithm is very complicated and the local matroid search algorithm can not search all optimal codes, this paper proposesa variable matroid search algorithm to search the quasi-cyclic codes by researching matroid search algorithm. The algorithm reduces the computational complexity by reducing the repeated search. Based on this algorithm, the systematic binary quasi-cyclic codes of which the rate is 1/are constructed. With the change of integer, the optimal codes of rate 1/can be obtained by the generator matrix reducing or adding a loop matrix. Through experiments, two new codes of which the minimum distance is larger than the existing optimal codes are worked out, which indicate the feasibility and superiority of the algorithm.
Matroid theory; Quasi-cyclic codes; Minimum distance; Variable matroid search algorithm
TN911.22
A
1009-5896(2016)11-2916-06
10.11999/JEIT160074
2016-01-19;改回日期:2016-06-15;
2016-09-01
巫光福 wuguangfu@126.com
国家自然科学基金(11461031, 61562037),江西省自然科学基金(20151BAB217016)
The National Natural Science Foundation of China (11461031, 61562037), The Natural Science Foundation of Jiangxi Province (20151BAB217016)
张水平: 男,1965年生,教授,研究方向为安全技术及工程、计算机应用技术、云计算.
林平平: 男,1991年生,硕士生,研究方向为信息论与编码.
巫光福: 男,1977年生,讲师,研究方向为信息论与编码、密码学、组合设计、概率统计.
