面向癫痫脑电图信号识别的径向基最小最大概率分类树

邓赵红 陈俊勇 刘解放 王士同



面向癫痫脑电图信号识别的径向基最小最大概率分类树

邓赵红*陈俊勇 刘解放 王士同

(江南大学数字媒体学院 无锡 214122)

脑电图(EEG)信号检测和识别是癫痫病的重要诊断手段。径向基函数神经网络具有出色的逼近能力和泛化性能，能直接识别出不同状态的脑电信号，但其透明性和可解释性差，忽视了不同类别数据间可分性的不同。对此，该文提出一种基于径向基函数神经网络和最小最大概率决策技术的分类树，采用一对一策略和排除法，更多考虑了类间可分性的不同。针对脑电信号识别的实验表明，所提方法结构清晰，分类能力强，可解释性更好。

脑电信号；径向基函数神经网络；最小最大概率；分类树

1 引言

癫痫是由大脑神经元突发性异常过度放电引发的大脑短暂性功能障碍，年发病率较高。脑电图信号的检测和识别是诊断癫痫病最为重要的手段。多种特征提取和智能识别的方法已被应用于癫痫脑电信号的识别，主要包括傅里叶变换[1,2]、小波分解等特征抽取方法和决策树[2]、模糊系统[3]、人工神经网络等分类方法。

文献[9]将径向基函数神经网络用在癫痫(ElectroEncephaloGram, EEG)信号的分类识别中。径向基函数(Radial Basis Function, RBF)神经网络具有一般神经网络的优点，如很强的非线性拟合能力及鲁棒性，此外，它还具有全局最佳逼近特性，不存在局部极小问题。但径向基函数神经网络的不足是其可解释性差，不易解释其推理过程和依据，因而不够透明。在处理多分类问题时，径向基函数神经网络一般不考虑各类之间不同的可分性，利用回归的方法直接进行多分类，从而导致分界面也过于复杂、难以描述。

文献[2]采用基于决策树和快速傅里叶变换的混合模型来对EEG信号进行分类。决策树分类器的优势正在于其可解释性和透明性，易于理解。然而，决策树是层次结构的，不可避免地存在自上而下的“误差积累”[10]，即如果在某个节点上发生了分类错误，则会把错误延续到后续节点上。为了降低积累的误差，应当优先使用可分性强的分类器，即先做把握大性的决策。

本文针对上述癫痫脑电信号识别方法存在的不足，通过引入最小最大概率学习机制来探讨相应的改进方法。文献[11,12]中提出的最小最大概率机在完成模型参数学习的同时，可实现错分概率上界的最小化。理论上说，此错分概率上界的指标越小，表明两类数据间的可分性越强，分类模型的可靠性越好，即更有把握得到正确的分类结果。文献[13]将之用于TSK型模糊系统分类器的学习，得到了透明性、可解释性更好的分类模型。考虑到RBF神经网络与模糊推理系统在一定的条件下存在等价性[14]，可采用一对一的策略和排除法，将最小最大概率机用于RBF神经网络分类器的学习，进而基于错分概率上界可构建更为透明和可靠的分类树。

本文首先介绍了RBF神经网络，最小最大概率机和分类决策树的相关知识，而后提出了一种基于RBF神经网络和最小最大概率决策技术的多分类决策树，并将之用于癫痫EEG信号的分类与识别。实验部分，通过3组不同分类目标的对比实验，证实了所提方法有着更好的可靠性和可解释性。

2 相关工作

2.1 RBF神经网络

RBF神经网络(Radial Basis Function Neural Network, RBFNN)[9]能够以任意精度逼近任一连续函数，具有良好的泛化能力。一个最简单的RBF神经网络是具有单隐层、单输出的3层结构的前馈神经网络，如图1所示。对于分类问题，通过隐层的非线性映射，通常可将原始特征空间上线性不可分的问题变换为高维特征空间上易于线性可分的问题。RBFNN的输出可用隐节点输出的线性组合来表示。

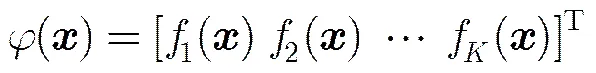
图1 单隐层单输出RBF神经网络

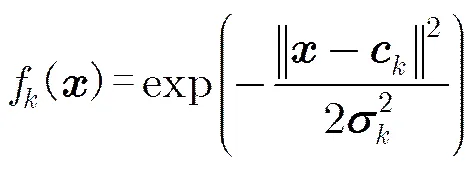
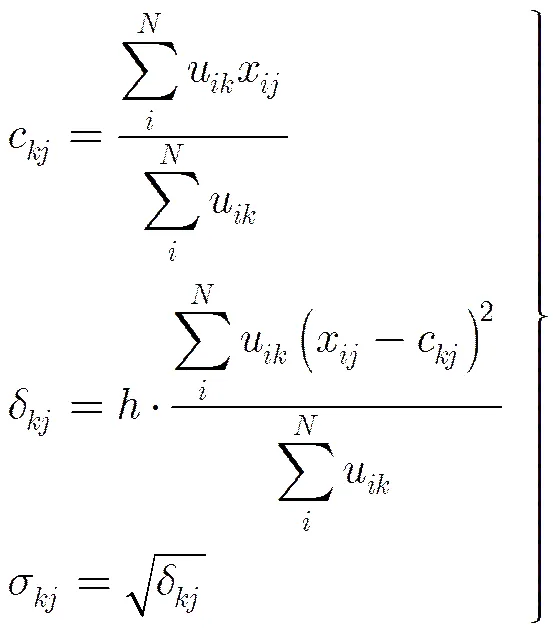
2.2 最小最大概率机

最小最大概率机(Minimax Probability Machine, MPM)[11,12]是基于错分概率上界最小化而设计的二分类模型。设有两类服从均值和协方差分别为和分布的维向量和。最小最大概率机定义了如式(5)的优化目标来确定一个分类超平面。

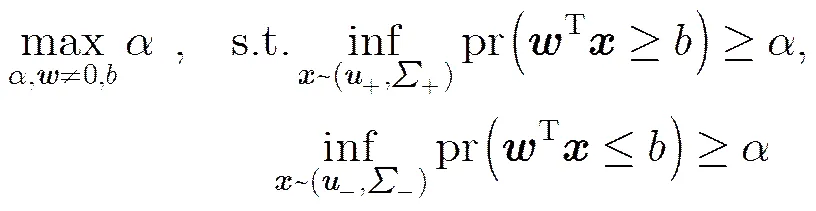
进一步，为了便于求解式(5)对应的优化问题，文献[11,12]推出了如下的定理。

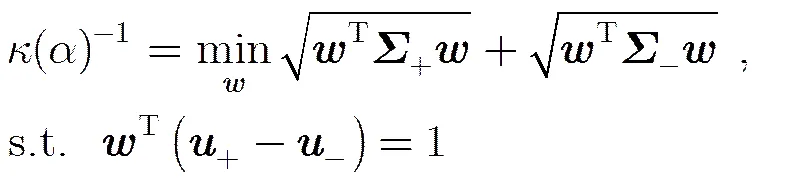
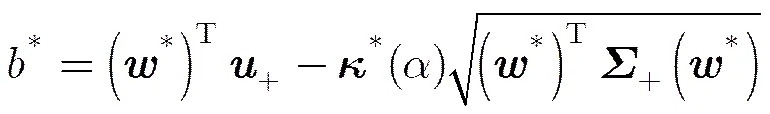
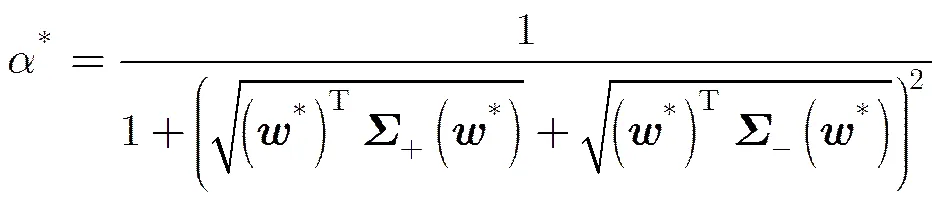
图2 最小最大概率机的几何解释

此外，由于线性的最小最大概率机的分类性能有限，文献[11,12]通过引入核技巧，给出了核化版本的最小最大概率机来实现非线性分类，求解过程和线性版本大致相同。

2.3 分类决策树

决策树(Decision Tree, DT)[2,10]是一种非度量方法，结构形如一棵倒置的树，其由节点和有向边组成，其中节点又分作内部节点和叶节点。内部节点表示一次查询操作，叶节点代表一个结果。决策树被用来分类时，数据由根节点出发，通过对一系列问题的回答，最终到达叶节点，得到叶节点所代表的类标记。其中，后一个问题的提法依赖于前一个问题的回答。

相较于神经网络等度量方法，分类树的优点是可解释性强，分类速度快，通过有限的查询，即可确定数据所属类别。

3 最小最大概率RBF神经网络

文献[13]采用最小最大概率机来训练TSK型模糊系统分类器，得到了透明性、可解释性更好的分类模型。考虑到RBF神经网络与TSK型模糊系统在一定的条件下存在等价性[14]，基于最小最大概率机和RBF神经网络，本文定义了如下形式的优化目标来学习一个可进行二分类的最小最大概率RBF神经网络(Minimax Probability RBF Neural Network, MP-RBFNN)。

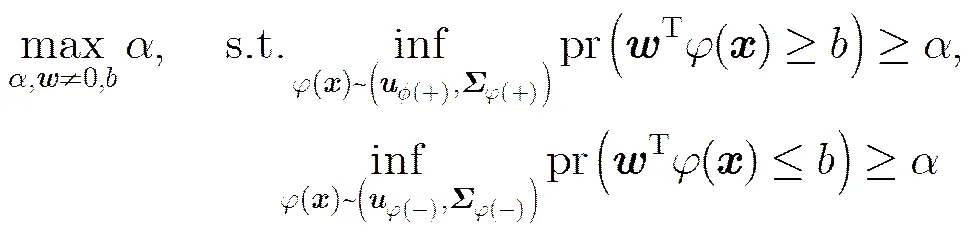
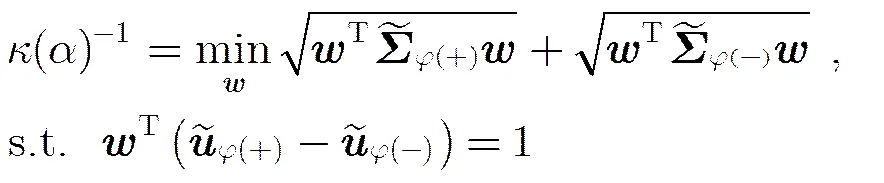
如此便可用文献[12]中的方法来求解。

4 MP-RBFNN与分类树

4.1 多分类问题

经典的RBF神经网络通常利用回归的方式进行多分类，例如，对于3类分类问题，训练时期望的输出可表示为,和，测试时则把实际输出分量最大的下标作为判定的类别，相当于用到了3个“一对多”(One-Against-Rest, OAR)的二元分类器。而文献[17,18]指出多数情况下“一对一”(One-Against-One, OAO)策略要优于OAR，因为OAR策略将余下的类别混为一类，易造成分类界面的复杂化。

OAO策略可将一个完整的多分类问题化解成多个二分类子问题，最终训练得到个二元分类器，相较于OAR策略，每一个二分类子问题难度小些，易于找到简单有效的分界面，也易于解释。利用OAO策略进行测试时，一般配合采用的是“投票法”。然而，投票法的问题是会出现多个类的票数相同的情况(拒分现象)，且对每一个输入数据都需要次比较。

4.2 径向基最小最大概率分类树

在OAO策略下，为了避免投票法的拒分问题和提升分类模型的效率，本文采用排除法来构建分类决策树，树的每个内部节点都是一个二元分类器。即沿着树生长的方向做排除法，只需次比较，即可获得分类结果。同时，为了降低树形结构固有的“误差积累”，本文将充分利用最小最大概率技术所提供的指标，优先选用指标大的二元分类器，即先做把握性大的分类。

本文提出的径向基最小最大概率分类树(Radial Basis Minimax Probability Classification Tree, RB-MP-CT)，训练和测试过程可如表1所示。

表1 RB-MP-CT的训练和测试过程

在余下的分类器中选择子节点时，通常不会出现两个二元分类器的指标大小相等的情况。而如果出现这样的小概率事件，一般可以简单处理，任选其中一个分类器作为子节点。

为了直观地解释多分类决策树，现举例如下进行说明：设有4类数据，利用OAO策略共得到6个二元分类器，之间的大小关系为>>>>>，那么先被选为分类树的根节点。再按照训练步骤5，先向左分支，认为样本不属于第4类，那么接下来子节点待选的分类器为,和，从中选择与第1类有关的指标最大者，即为。再进1层，若排除样本属于第3类的可能，则最终选择作为左侧的子节点。如此重复，得到的即是一个4层的完全二叉树(如图3)。

5 实验研究

5.1 实验数据

本部分针对德国波恩大学提供的癫痫EEG信号数据设计实验。该数据集分为5组，每组数据包含100个23.6 s长度，采样频率为173.61 Hz的EEG信号片段(4097个采样点)。各组数据的具体情况如表2所示。图4表示的是各组数据中第1个EEG信号的波形(即A001, B001, C001, D001和E001)，更多细节可参见文献[19]。

图3 RB-MP-CT

图4 各组首个EEG信号的波形

表2 EEG数据集的组成和描述

5.2 特征提取

为了有效地识别EEG信号，通常需要对原始信号做一些变换来提取特征[20]。这里部分借鉴了文献[3,8]的特征提取方法，通过离散小波变换(Discrete Wavelet Transform, DWT)和统计方法来提取特征量。采用了二阶Daubechies小波[21]，将长为4097的EEG信号分解成了4层(如图5)。首先，分解得到第1层小波的近似系数(低频分量)和细节系数(高频分量)，然后，进一步分解，得到和，以此类推，即得到5个子带，如图6所示。设，各层系数的长度为

在此基础上，每个子带的最大值、最小值、均值和标准差被统计出来，得到20维的特征向量。实验中，这些特征被统一地归一化到区间。

5.3 实验设置

从表1，图4和图6中可以看到，E组信号变化最为强烈，A组信号波形与B组相似，C, D组信号表现得比A, B组信号弱。不同的场景下，会有不同的分类目标，本文设计了3组实验：Expt-1将健康和患病的EEG信号分作2类，Expt-2将健康、患病间隙期和患病发作期的EEG信号分作3类，Expt-3将每一组EEG信号分作一类。

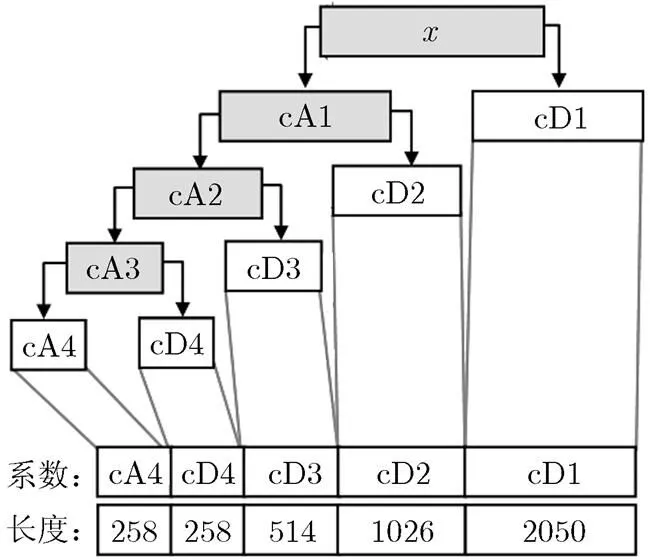
图5 DWT分解EEG信号过程

图6 各组首个EEG信号的小波系数带

实验以MATLAB 8.1为平台，以线性和核化的MPM，文献[4,8]中多层感知器神经网络(MLPNN)，以及MATLAB工具箱中的RBFNN, DT为对比算法，与本文提出的RB-MP-CT进行了比较。其中MPM(linear)和MPM(kernel)用于多分类时采用了OAO策略和投票法，RBFNN采用多输出回归进行直接多分类。各组实验都采用了5折交叉验证的策略进行参数选优。

实验以“均值±标准差”的形式给出各算法对数据集分类的测试精度、敏感度和特异度[3,8]，以及MPM相关算法对相关模型训练所得的指标。

5.4 结果分析

各组实验结果如表3~表5，图7所示。从结果来看，各组实验中，本文方法都有很好的表现，在Expt-1和Expt-2中的分类精度达到0.95以上，在Expt-3中的分类精度能达到0.81。Expt-1和Expt-2中，分类任务较为简单，MLPNN和RBFNN同本文方法的分类精度是相当的。但在Expt-3中，分类的类别数为5，这时RBFNN没有找到最佳的分界面，而本文方法采用OAO策略则比较容易找到多个简单有效的分界面。

同MLPNN的结果相比，本文方法在同等条件下体现出了更好的有效性和可靠性。对AB-CDE的分类，本文方法实验所得分类精度为0.9680，略高于MLPNN。文献[8]中MLPNN对AB-CDE的分类精度高达98.8%，文献[4]同样使用了MLPNN对AB-CDE的分类精度则为93.2%，主要因为特征提取和实验方案存在不同。对AB-CD-E的分类，本文方法实验所得分类精度与文献[8]中取得的95.6%的分类精度是相近的，而在敏感性上好于文献[8]中的结果。在分5类时，本文方法取得的结果略好于MLPNN，明显好于DT等。

由于决策阶段采用了分类树结构，所以本文方法显得简洁高效，图7显示只需4次比较即可判定类别，而投票法则需10次比较，并可能存在拒分现象。相比传统的DT算法，本文方法结合了RBF神经网络，因而拥有更好的非线性逼近能力和泛化性能。由于优先选用指标大的分类器，最大程度降低了积累误差。

图7 Expt-3中RB-MP-CT训练所得模型

5 结束语

针对癫痫EEG信号识别，结合已有研究成果，本文提出了新的解决方案。为充分利用不同组信号之间的可分性，本文采用最小最大概率技术来学习RBF神经网络的权值参数，进一步在OAO策略和排除法下，利用学习得到的指标构造可靠的分类树，得到简洁高效的多分类模型。实验结果证实了本文方法有很强的非线性分类能力，同时其可解释性更好，推理过程清晰。然而，由于采用了一对一策略，类别数多的时候，模型训练工作会比较繁重，这是需要改进的地方。在余下的分类器中选择子节点时，如果出现两个分类器的指标大小相等的情况，是否有更好的处理方式，这在未来工作中也有待深入探讨。

表3 Expt-1中各算法性能指标

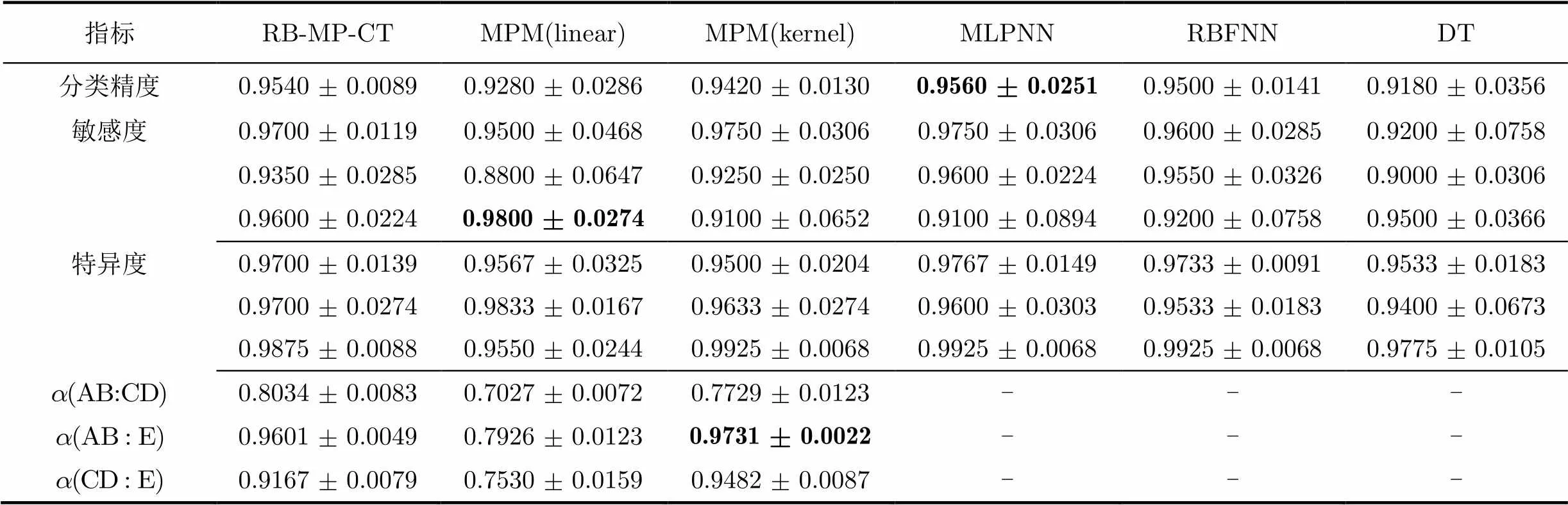
表4 Expt-2中各算法性能指标

表5 Expt-3中各算法性能指标

[1] VENEMA V, AMENT F, and SIMMER C. A stochastic iterative amplitude adjusted Fourier transform algorithm with improved accuracy[J]., 2006, 13(3): 321-328. doi: 10.5194/npg-13- 321-2006.

[2] POLAT K and GÜNESŞ S. Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform[J].&, 2007, 187(2): 1017-1026. doi: 10.1016/j.amc. 2006.09.022.

[3] INAN G and ELIF DERYA U. Adaptive neuro-fuzzy inference system for classification of EEG signals using wavelet coefficients[J]., 2005, 148(2): 113-121. doi: 10.1016/j.jneumeth.2005.04.013.

[4] SUBASI A. EEG signal classification using wavelet feature extraction and a mixture of expert model[J]., 2007, 32(4): 1084-1093. doi: 10.1016/ j.eswa.2006.02.005.

[5] 王登, 苗夺谦, 王睿智. 一种新的基于小波包分解的EEG特征抽取与识别方法研究[J]. 电子学报, 2013, 41(1): 193-198. doi: 10.3969/j.issn.0372-2112.2013.01.33.

WANG Deng, MIAO Duoqian, and WANG Ruizhi. A new method of EEG classification with feature extraction based on wavelet packet decomposition[J]., 2013, 41(1): 193-198. doi: 10.3969/j.issn.0372-2112.2013. 01.33.

[6] SRINIVASAN V, ESWARAN C, and SRIRAAM A N. Artificial neural network based epileptic detection using time-domain and frequency-domain features[J]., 2005, 29(6): 647-660. doi: 10.1007/ s10916-005-6133-1.

[7] VAIRAVAN S, CHIKKANNAN E, and NATARAJAN S. Approximate entropy-based epileptic EEG detection using artificial neural networks[J]., 2007, 11(3): 288-295. doi: 10.1109/TITB.2006.884369.

[8] Orhan U, Hekim M, and Ozer M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model[J]., 2011, 38(10): 13475-13481. doi: 10.1016/ j.eswa.2011.04.149.

[9] ASLAN K and HSAHIN B. A radial basis function neural network model for classification of epilepsy using EEG signals[J]., 2008, 32(5): 403-408. doi: 10.1007/s10916-008-9145-9.

[10] 连可, 陈世杰, 周建明, 等. 基于遗传算法的SVM多分类决策树优化算法研究[J]. 控制与决策, 2009, 24(1): 7-12. doi: 10.3321/j.issn:1001-0920.2009.01.002.

LIAN Ke, CHEN Shijie, ZHOU Jianming ,. Study on GA-based SVM multi-class classification decision-tree optimization agorithm[J]., 2009, 24(1): 7-12. doi: 10.3321/j.issn:1001-0920.2009.01.002.

[11] LANCKRIET G, GHAOUI L E, BHATTACHARYYA C,. Minimax probability machine[C]. Advances in Neural Information Processing Systems, Vancouver, British Columbia, Canada. 2001: 801-807.

[12] LANCKRIET G R G, GHAOUI L E, BHATTACHARYYA C,. A robust minimax approach to classification[J]., 2002, 3(Dec): 555-582. doi: 10.1162/153244303321897726.

[13] DENG Z, CAO L, JIANG Y,. Minimax probability TSK fuzzy system classifier: A more transparent and highly interpretable classification model[J]., 2015, 23(4):813-826. doi:10.1109/TFUZZ. 2014.2328014.

[14] Rubio-Solis A and Panoutsos G. Interval type-2 radial basis function neural network: A modeling framework[J]., 2015, 23(2): 457-473. doi: 10.1109/TFUZZ.2014.2315656.

[15] 陈聪, 王士同. 基于模糊分组和监督聚类的RBF回归性能改进[J]. 电子与信息学报, 2009, 31(5): 1157-1160.

CHEN Cong and WANG Shitong. Improved RBF regression using fuzzy partition and supervised fuzzy custering[J].&, 2009, 31(5): 1157-1160.

[16] ROTH P M, HIRZER M, KÖSTINGER M,. Mahalanobis Distance Learning for Person Re-identification [M]. London: Person Re-Identification, 2014: 247-267. doi: 10.1007/978-1-4471-6296-4_12.

[17] Kang S, Cho S, and Kang P. Constructing a multi-class classifier using one-against-one approach with different binary classifiers[J]., 2014, 149, Part B(PB): 677-682. doi: 10.1016/j.neucom.2014.08.006.

[18] Galar M, Fernández A, and Barrenechea E. An overview of ensemble methods for binary classifiers in multi-class problems: Experimental study on one-vs-one and one-vs-all schemes[J]., 2011, 44(8): 1761-1776. doi: 10.1016/j.patcog.2011.01.017.

[19] ANDRZEJAK R G, LEHNERTZ K, MORMANN F,. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state[J]., 2001, 64(6): 061907. doi: 10.1103/PhysRevE.64. 061907.

[20] Parvez M Z and Paul M. Epileptic seizure detection by analyzing EEG signals using different transformation techniques[J]., 2014, 145(18): 190-200. doi: 10.1016/j.neucom.2014.05.044.

[21] ROY V and Shukla S. Automatic removal of artifacts from EEG signal based on spatially constrained ICA using daubechies wavelet[J].(), 2014, 6(7): 31-39. doi: 10.5815/ijmecs.2014.07.05.

Radial Basis Minimax Probability Classification Tree for Epilepsy ElectroEncephaloGram Signal Recognition

DENG Zhaohong CHEN Junyong LIU Jiefang WANG Shitong

(,,214122,)

ElectroEncephaloGram (EEG) signal detection and recognition is an important diagnostic method for the epilepsy. Radial Basis Function (RBF) neural network has excellent performance on approximation and generalization, and can directly recognize EEG signals in different states. However, its transparency and interpretability are low, and it also ignore the different separabilities between different classes of data. In this paper, a classification tree based on RBF neural networks and minimax probability decision technique is proposed, using one-against-one and exclusive method and paying much attention to the different separabilities among classes. Experiments on EEG signals show that the proposed method has clear structure, strong classification ability and better interpretability.

ElectroEncephaloGram (EEG) signal; Radial basis function neural network; Minimax probability; Classification tree

R741.044; TP183

A

1009-5896(2016)11-2848-08

10.11999/JEIT160082

2016-01-19；改回日期：2016-06-08；

2016-09-01

邓赵红 dengzhaohong@jiangnan.edu.cn

江苏省杰出青年基金(BK20140001)，上海市科学技术委员会扬帆项目(14YF1411000)，上海市教委创新项目(14YZ131)

The Youth Fund of Jiangsu Province (BK20140001), YangFan Project of Shanghai Municipal Science and Technology Commission(Grant No. 14YF1411000), The Innovation Program of Shanghai Municipal Education Commission (Grant No. 14YZ131)

邓赵红： 男，1981年生，教授，博士，从事人工智能和神经模糊计算的研究.

陈俊勇： 男，1990年生，硕士生，研究方向为人工智能和神经模糊计算.

刘解放： 男，1982年生，博士生，研究方向为人工智能和模式识别的研究.

王士同： 男，1964年生，教授，博士生导师，从事人工智能和模式识别.