基于独立向量分析的脑电信号中肌电伪迹的去除方法

陈 强 陈 勋 余凤琼



基于独立向量分析的脑电信号中肌电伪迹的去除方法

陈 强①陈 勋*①余凤琼②

①(合肥工业大学生物医学工程系 合肥 230009)②(安徽医科大学医学心理学系 合肥 230032)

脑电数据经常被各种电生理信号伪迹所污染。在常见伪迹中，肌电伪迹特别难以去除。文献中最常用的方法包括诸如独立分量分析(Independent Component Analysis, ICA)和典型相关分析(Canonical Correlation Analysis, CCA)等盲源分离技术。该文首次提出一种基于独立向量分析(Independent Vector Analysis, IVA)的新方法，用以去除脑电中的肌电伪迹。IVA同时使用高阶统计量和二阶统计量，因此该方法能够充分利用肌电伪迹的非高斯性和弱相关性，兼具ICA方法和CCA方法的优势。实验表明，使用IVA方法可以在保留脑电成份的同时极大抑制肌电伪迹，效果显著优于ICA法和CCA法。

脑电；肌电伪迹；盲源分离；独立向量分析

1 引言

众所周知，存在于脑电数据的各种电生理伪迹干扰中，肌肉收缩(例如咬合、咀嚼、皱眉等动作)产生的肌电伪迹很难去除[1,2]。显然，在脑功能分析[3]、脑-机接口[4,5]等应用研究中，能否获取纯净的脑电信号是关键的一步。如文献[2]所述，去除肌电伪迹的难点在于其幅度高、频带宽、分布位置多变。由于生理过程复杂并且缺乏参考信号，脑电处理中常用盲源分离技术来去除肌电伪迹[6,7]。

作为一种著名的盲源分离技术，独立分量分析(Independent Component Analysis, ICA)已被广泛应用于脑电中的肌电伪迹去除[7,8]。在ICA中，通过高阶统计将多道EEG数据线性解混为统计独立的成分，去除其中类似肌电伪迹的成分后，重建得到干净的数据。尽管很多研究者推荐ICA[8,9]，但是也有文献中对ICA去除肌电伪迹的效果提出质疑[2,10]，认为ICA比较适合去除空间分布较为固定的肌电伪迹，然而肌电伪迹的形状和幅度取决于肌肉收缩的程度、肌肉的类型和数量，其空间分布经常变化。文献[11]指出，大多数独立成分实际上同时包含脑电和肌电。

典型相关分析(Canonical Correlation Analysis, CCA)作为另一种盲源分离技术也被用于肌电伪迹的去除[6,12]。CCA的目标是利用二阶统计量提取出自相关系数最大的源，同时这些源彼此互不相关。相比脑电，肌电波形更接近白噪声，因此自相关系数相对更低，CCA利用这个有区分度的特征从脑电中去除肌电伪迹。文献[6,12,13]显示，对于仿真数据，CCA比ICA表现更好。临床应用也表明CCA对去除肌电伪迹的效果有所改善[14,15]。该方法在单道EEG去除肌电干扰的研究中也表现出优越性[16]。

最近的报道[8]指出，方法的性能表现与所处理的脑电数据高度相关。得以利用肌电信号的非高斯性，使用高阶统计量的ICA获得统计意义上的独立源；而通过利用肌电信号的低自相关性，使用二阶统计量的CCA得以获取自相关特征。虽然在理论上，两个信号源如果互相独立则必然互不相关，但在具体的ICA算法中，只能使用某些高阶统计量作为判据，未必能适应复杂多变的肌电伪迹。所幸ICA和CCA二者使用的统计信息是可以互补的。本文的目标是将CCA和ICA的优点集成在一个盲源分离框架内，即同时使用二阶统计量和高阶统计量来更好地求解去噪问题。

独立向量分析(Independent Vector Analysis, IVA)[17]是最近兴起的这样一种盲源分离技术。IVA可以看作是ICA从一个数据集扩展到多个数据集。IVA利用信息论判据将每个数据集分解为统计独立的源，同时利用数据集之间的相关信息使得数据集的各对应的源彼此相关。利用二阶统计量表示多数据集之间的相关信息时，使对应的源相关值最大，这正是CCA解决去噪问题的优势所在。因此，IVA很自然地结合了ICA和CCA二者的优势，理论上比单独使用ICA和CCA使用更多的信息，预期能比只用其中一种方法取得更好的源分离效果。因此本文提出在IVA框架下结合二阶统计量和高阶统计量，从多道脑电数据中去除肌电伪迹的方法。本文在仿真数据上验证IVA方法，并与常用的ICA和CCA方法进行对比。

2 在独立向量分析框架下去除肌电伪迹

2.1独立向量分析

IVA是近年提出的一种新型盲源分离技术[18]，其本质是将独立分量分析技术扩展到多个数据集上，充分利用多数据集之间的统计关联性，同时用高阶统计量和二阶统计量对数据集进行分解。IVA的目标是使每个数据集中的各个源是相互独立的，且一个数据集中的某个源至多只与其他数据集中的一个源相关。

设有个数据集，每个数据集由个独立源线性混合而成。

IVA可以通过使代价函数最小化，即个SCV之间的互信息量最小化，来确定源成分向量。

对于给定的多组数据集，可以通过基于梯度下降、牛顿-拉弗森迭代算法等方法来估计各个数据集的混合矩阵和信号源。

2.2 基于IVA去除肌电伪迹的思路和算法

实际测量的脑电信号很可能包含肌电伪迹。由于电极在头部位置不同，肌电伪迹在各导联上的波形有差异；并且不同被试者、不同部位肌肉、不同收缩状态下所产生的伪迹也会有差异，这种信号复杂性导致肌电伪迹难以去除。

目前去除脑电信号中肌电伪迹的算法中，一类是利用高阶统计量的ICA算法，基于肌电伪迹与脑电信号统计独立的设定，将数据集分解为尽可能独立的源成分，然后选择去除其中类似肌电的成分；另一类是利用二阶统计量的CCA算法，其依据是肌电伪迹波形相比脑电更接近白噪声，因而自相关性也明显小于脑电，数据集分解后将自相关系数小的成分视为肌电。由于肌电伪迹的复杂多变，两类算法都存在一定的适应性问题[8]。既然两类算法所利用的信息不同，那么如果能相互结合，就有可能取得更好的去肌电伪迹的效果。

如前所述，IVA并非只用高阶统计量分别处理各数据集成为独立源，而是使用了信息论判据将多个数据集分解为多个SCV。如前述SCV的定义，每个SCV是由不同数据集中各取一个源成分构成，因此IVA的分解过程还利用了数据集相互之间的关联信息。IVA不仅可以将每个数据集分解成个尽可能独立的信号源，还可以保证各数据集相对应位置的源成分是相关的。IVA结合利用了高阶统计量和二阶统计量，兼具ICA和CCA的特点，因此本文提出了基于IVA的去除肌电伪迹的算法框架。

使用IVA去除脑电中肌电伪迹的算法思路如图1所示。设有道脑电数据集，由个独立源线性混合而成。将该数据集做时间延迟，得到数据集，即将中每个导联数据序列右移一个采样点。使用IVA算法，分解出个SCV，则每个SCV中的2个向量是2个源数据集和中各取一个源成分。IVA分解的结果使得2组独立源成分数据集中相对应位置的信号源是相关的，即每个SCV中的2个向量在二阶统计上彼此最接近，而与其他任何SCV中的向量在二阶统计上差异大。而我们知道，相对于头皮脑电，头部体表肌电的带宽更大，且频谱特征更接近白噪声。因此在相同延时的情况下，体表肌电成分的自相关系数明显小于头皮脑电成分的自相关系数。则按各SCV中成分的互相关系数大小排序后，与肌电伪迹成分有关的SCV必然位于与脑电相关的SCV之后。如图1所示，设置阈值，则相关系数较小的几个SCV中所含的源成分可视为肌电伪迹成分，将其置零，得到相应的去除肌电伪迹成分的数据集源矩阵和。最后根据IVA求解出的混合矩阵，估计去除肌电伪迹的脑电信号。

算法框架概括如下：

3 实验数据及分析

3.1 评测数据的获取

3.1.1采集纯净脑电数据 脑电数据采集使用NeuroScan公司的NuAmps系统，采用直流耦合，70 Hz低通，采样频率为1000 Hz, A/D为32 bit，开启50 Hz陷波。被试者为6名健康大学生志愿者(3男3女，年龄21~23岁)。电极放置按国际10-20系统，共采集19导联数据：FP1, FP2, F7, F3, Fz, F4, F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, O1, O2。参考电极置于右耳垂。要求被试者安静闭眼并保持端正坐姿，以避免眼电、头颈部肌电等伪迹的产生。由有经验的神经生理学专家通过波形观察和谱分析，对每个被试记录下的脑电信号，各选择一段无肌电干扰的10 s数据波形段，存为19×10000的矩阵。6名被试，共获得6段纯净的背景脑电。

3.1.2获取纯净肌电伪迹 数据采集系统及设置与采集纯净脑电数据时相同。被试者为4名健康大学生志愿者(3男1女，年龄21~22岁)。要求以上被试者闭眼状态下分别完成以下任务：咀嚼、持续保持张嘴和头部保持向左、向右侧倾，使采集的信号中含有强烈的肌电伪迹。所采集的信号使用SOBI(Second Order Blind Identification)[19]进行分解。分解出的成分通常既有肌电成分，也有脑电成分。然而某些情况下，有经验的神经生理学专家可以观察到某些成分在一段内只有肌电而无脑电成分，从4个被试者的数据中各挑选一段10 s的纯肌电成分，并按分解矩阵重构至19导联脑电形式。然后将4个重构纯肌电干扰信号求和，得到包含4个独立肌电成分的参考信号，存为19×10000的矩阵[6]。该合成肌电伪迹信号有4个独立肌电成分，特别是咀嚼动作产生的阵发性肌电伪迹，使得肌电伪迹的空间分布是变化的，更接近实际测量时的情况。

图1 在IVA框架下去除肌电伪迹的示意图

3.1.3生成仿真信号 将包含纯肌电成分的信号叠加至纯净脑电信号上，生成仿真信号。

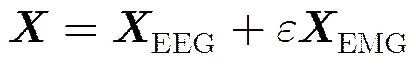
信号的均方根定义为

则仿真信号的信噪比为

3.2 去肌电伪迹效果的评价指标

定义相关系数(Correlation Coefficient, CC)为与对应各导联信号相关系数的均值。

定义相对均方根误差为

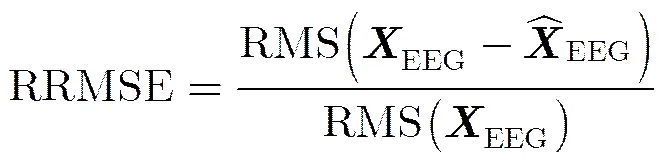
3.3对照算法

3.3.1 ICA 脑电信号中各成分与其他伪迹可以看作是由多个独立源产生，因此ICA被广泛应用于脑电信号处理中。在低维空间中，特征矩阵联合近似对角化(JADE)[20]与不动点ICA算法相比，收敛速度快，已被用于去除脑电信号中的肌电伪迹[1]。首先采用JADE分解各数据集信号，然后人工判断肌电成分并置零后重建，以去除肌电伪迹。

3.3.2 CCA CCA是用于分析两组随机变量之间相关性程度的一种经典统计分析方法[21]，能够有效地揭示两组随机变量之间的相互线性依赖关系。其基本原理是在分解信号源时，假定潜在信号源互不相关，同时使得各个信号源最大自相关，并按照分解的信号源的自相关值排序。近年来，CCA被用于脑电分析[22]，这是由于肌电等伪迹更接近于噪声信号，自相关值较小。因此可以将使用原始脑电作为第1个数据集，延时后的数据作为第2个数据集，使用CCA分解后，具有较小自相关值的分量视为肌电伪迹，置零后重建，即可得到去除肌电伪迹的脑电信号。

3.4 IVA, ICA, CCA对仿真数据去除肌电效果的比较

我们对各组纯净EEG信号生成了不同SNR (0.25~4.00 dB)的仿真信号，分别用IVA, ICA (JADE)和CCA 3种方法去除肌电伪迹，并估计恢复信号所对应的CC值和RRMSE值。

图2所示为一组仿真信号的处理实例，在纯净EEG上叠加较强肌电伪迹，然后分别用ICA(JADE), CCA和IVA共3种方法处理。3种方法都能有效去除肌电干扰，但是用肉眼即可分辨，ICA和CCA处理结果中，某些导联存在肌电伪迹，与原始纯净信号有明显差异。如图3所示为该段信号中T3导联的处理结果，其中图3左下图和右下图分别是两小段信号使用ICA, CCA和IVA滤波结果。其中信号的浅色粗线条为原始纯净脑电，黑色细线条表示滤波后的结果。可以看到，在该导联有较强肌电干扰的情况下，ICA和CCA的处理结果均与原纯净脑电信号出现较大差异，误差不仅出现在肌电伪迹较强(0~2 s)的时段，也出现在肌电伪迹较弱(5~7 s)的时段。

对各组仿真信号处理结果的统计如图4所示。图4(a)表示各算法在不同SNR下CC值的均值和标准差。从图4(a)中可以看到，在肌电干扰较弱时(SNR>2 dB), ICA, CCA和IVA都可以取得接近于1的CC值，说明在肌电干扰相对较弱的情况下，3种算法所恢复的EEG信号均与原信号相似程度很高，去除肌电伪迹效果良好。但是当SNR下降，特别是SNR<1 dB时，ICA和CCA的CC值都开始随着SNR下降而明显下降，说明在肌电干扰相对较强的情况下，ICA和CCA去除肌电伪迹的效果都有所降低。我们注意到，此时IVA对应的CC均值没有明显下降，且CC值的偏差也较小。从实际滤波波形中也可以看到，IVA方法所恢复的波形与原纯净EEG的重合程度很好。图4(b)表示各算法在不同SNR下RRMSE值的均值和标准差。可以看到，在SNR较高的情况下，3种算法所得RRMSE值都较低，而SNR值较低的情况下，ICA和CCA算法的RRMSE值显著增高，说明此时去除肌电所得波形与原波形有较大差异，而IVA的RRMSE值仍保持在较低水平，表明其仍能获得较好的滤波效果，结论与使用CC判据的类似。

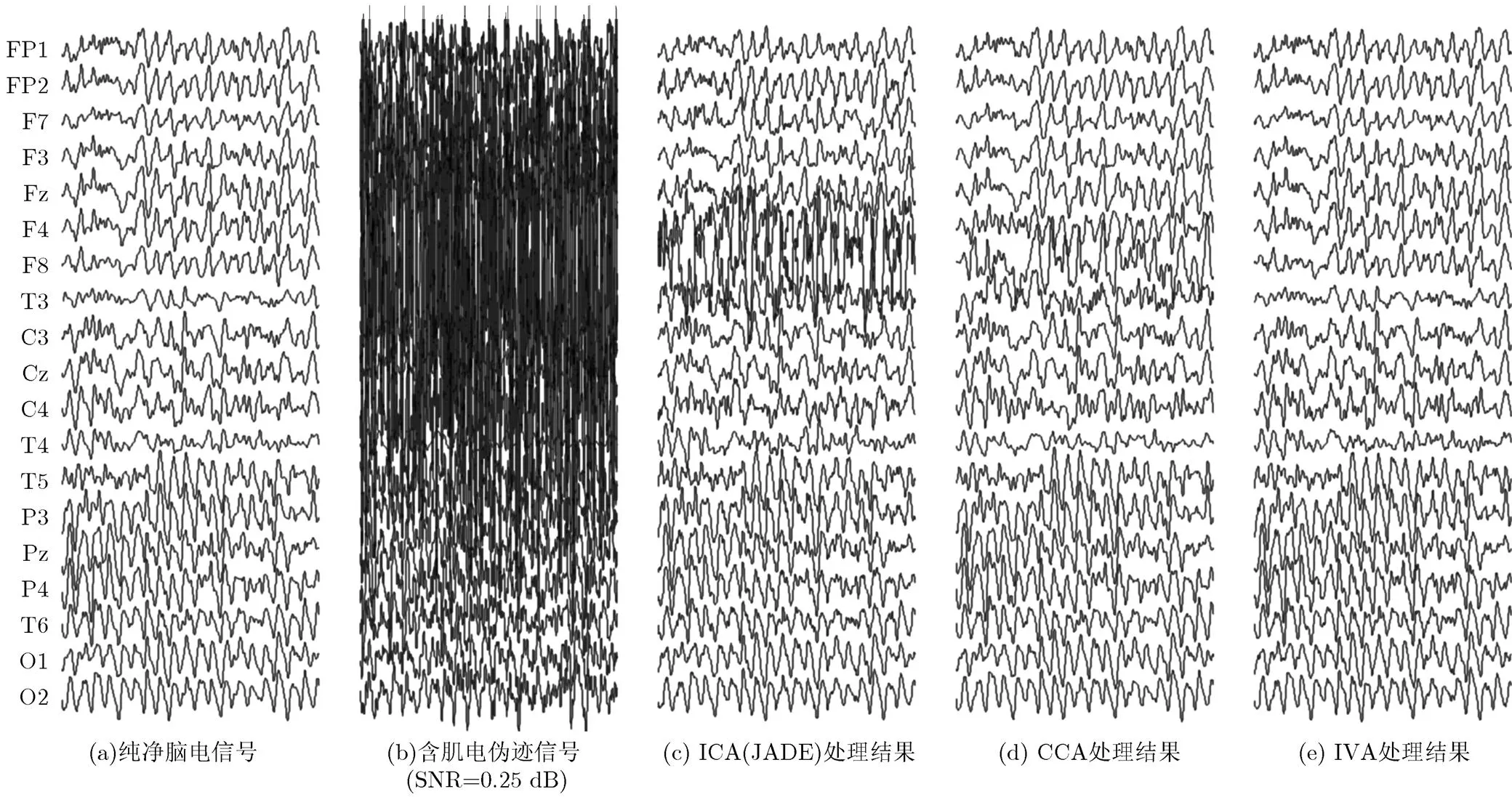
图2 ICA, CCA和IVA对仿真信号去除肌电伪迹的效果对比

图3 图2信号中T3导联信号分别使用ICA(JADE), CCA和IVA去除肌电伪迹效果实例(左下图和右下图中，浅色粗线为原始纯净脑电信号，黑色细线为运算结果)

图4 对于不同信噪比的仿真信号，ICA(JADE), CCA和IVA去除肌电伪迹效果的CC和RRMSE统计结果

3.5 IVA, ICA, CCA对真实数据去除肌电效果的比较

为验证算法的有效性，我们对真实的EEG信号使用IVA去除肌电伪迹，并与ICA(JADE)和CCA进行比较。数据来源是PhysioNet数据库中癫痫病患者的脑电[23]，导联数30，截取每段数据的时间长度10 s，图5(a)是其中一组数据，在3.8~5.2 s段有明显的肌电伪迹。图5(a)-图5(g)显示时长为10 s。图5(h)-图5(j)显示时长为1.2 s。图5(e)-图5(j)中浅色为原始信号，黑色为重构结果。

图5(b)为ICA(JADE)分解出的30个源成分，图中各源的自相关值自下而上递增。可观察到自相关值最小的4个独立源包含明显的肌电成分，而其他独立源的肌电成分不明显。图5(e)为去除自相关值最小的4个源之后的重建结果，局部放大如图5(h)所示，可以看到较大的肌电伪迹被抑制。但同时在原本肌电伪迹很小的信号段，滤波后的信号与原始信号出现较大区别，其原因是ICA分解的第3和第4个源中除了肌电伪迹以外还包含明显的脑电成分，未能有效分离。去除这两个成分会导致脑电信号受损，但是如果不去除这两个源成分则肌电伪迹不能很好消除。

图5(c)所示为CCA分解出的30个源成分，排列次序同图5(b)。可观察到约半数源含有肌电成分，并且含肌电伪迹的源同时也含有大量的EEG成分，说明CCA未能有效分离信号中的脑电与肌电伪迹，导致消除肌电伪迹与保留脑电信号发生矛盾。图5(f)所示为去除自相关最小的6个源之后的重建结果，局部放大如图5(i)所示。可以看到脑电信号同样有较大损失。

图5(d)所示为IVA分解出的30个源成分，排列次序同图5(b)。与ICA和CCA分解结果不同的是，只有自相关值最小的2个源包含明显的肌电成分，并且这2个源中的脑电成分相对其他源中的脑电成分较小，说明IVA能够较好地分离信号中的脑电和肌电伪迹。图5(g)是去除IVA分解的最后2个源之后的重建结果，局部放大如图5(j)所示。可以看到，在肌电伪迹强烈的信号段，肌电伪迹受到抑制；同时，在原本肌电伪迹很小的信号段，滤波后的信号与原始脑电信号基本重合，说明脑电信号得到很好的保留。

图5 真实脑电数据分别使用ICA(JADE), CCA和IVA去除肌电伪迹的结果

3.6对滤波效果差异的分析

ICA的目标是将信号分解为独立信号源，利用高阶统计量判断信号源的独立性，要求高斯分布的源不超过一个。而脑电和肌电通常为非高斯分布，因此适用ICA算法进行分析。同时，相比具有准周期性的脑电信号，肌电信号更接近噪声，因此相同延迟下的自相关值更低，利用二阶统计量的CCA可以有效分析。基于以上原因，ICA和CCA在脑电分析中都得到广泛应用。而本文在IVA框架下，结合利用高阶统计量和二阶统计量，在将信号分解为独立源的同时又使得数据集内各源按相关性排序，充分利用了肌电伪迹的非高斯性和弱自相关性，因此同时具有两种算法的优势。对仿真数据的分析显示，在肌电干扰较弱时，3种算法都可以有效去除肌电；而肌电伪迹较强且空间分布变化时，IVA的效果明显优于目前常用的ICA和CCA。

4 结束语

针对去除脑电信号中的肌电伪迹这一具有普遍性的问题，本文首次提出了基于独立向量分析(IVA)的肌电伪迹去除方法，并在仿真数据上与ICA和CCA算法使用相关系数和相对均方误差作为判据进行了比较。由于IVA算法同时使用二阶统计量和高阶统计量，得以充分利用肌电的非高斯性和低相关性两方面特征，更好地去除脑电中的肌电伪迹。实验结果表明，即使在有较强肌电伪迹且肌电空间分布变化的情况下，IVA算法仍然能够有效去除肌电伪迹，效果优于ICA和CCA，所估计的脑电波形与原始波形之间的均方误差小且关联性强，说明IVA算法是一种有效去除脑电信号中肌电伪迹的算法。IVA方法的主要问题是计算量较大，目前只适合离线分析。我们将进一步优化IVA去除肌电伪迹的效果，并探索简化计算的途径。

[1] URRESTARAZU E, IRIARTE J, ALEGRE M,. Independent component analysis removing artifacts in ictal recordings[J]., 2004, 45(9) 1071-1078. doi: 10.1111/ j.0013-9580.2004.12104.x.

[2] MCMENAMIN BW, SHACKMAN AJ, GREISCHAR LL,. Electromyogenic artifacts and electroencephalographic inferences revisited[J]., 2011, 54(1): 4-9. doi: 10.1016/j.neuroimage.2010.07.057.

[3] 闫铮, 高小榕, 应俊. 基于认知功能连接的信息流增益计算方法及应用[J]. 电子与信息学报, 2014, 36(11): 2756-2761. doi: 10.3724/SP.J.1146.2013.02019.

YAN Z, GAO X R, and YING J. The flow gain methods and applications based on cognition functional connectivity[J].&, 2014, 36(11): 2756-2761. doi: 10.3724/SP.J.1146.2013.02019.

[4] 吕俊, 谢胜利, 章晋龙. 脑-机接口中基于ERS/ERD的自适应空间滤波算法[J]. 电子与信息学报, 2009, 31(2): 314-318.

LÜ J, XIE S L, and ZHANG J L. Adaptive spatial filter based on ERD/ERS for brain-computer interfaces[J].&, 2009, 31(2): 314-318.

[5] 吴明权, 李海峰, 马琳. 单通道脑电信号中眼电干扰的自动分离方法[J]. 电子与信息学报, 2015, 37(2): 367-372. doi: 10.11999/JEIT140602.

WU M Q, LI H F, and MA L. Automatic electrooculogram separation method for single channel electroencephalogram signals[J].&, 2015, 37(2): 367-372. doi: 10.11999/JEIT140602.

[6] DE CLERCQ W, VERGULT A, VANRUMSTE B,. Canonical analysis applied to remove muscle artifacts from the electroencephalogram[J]., 2006, 53(12): 2583-2587. doi: 10. 1109/TBME.2006.879459.

[7] ALBERA L, KACHENOURA A, COMON P,. ICA- based EEG denoising: a comparative analysis of fifteen methods[J].-, 2012, 60(3): 407-418. doi: 10.2478/ v10175-012-0052-3.

[8] URIGUEN J A and GARCIA-ZAPIRAIN B. EEG artifact removal state-of-the-art and guidelines[J]., 2015, 12(3): 031001. doi: 10.1088/1741-2560 /12/3/031001.

[9] WINKER I, BRANDL S, HORN F,. Robust artifactual independent component classification for BCI practitioners [J]., 2014, 11(3): 035013. doi: 10.1088/1741-2560/11/3/035013.

[10] SHACKMAN AJ, MCMENAMIN BW, Slagter HA,. Electromyogenic artifacts and electroencephalographic inferences[J]., 2009, 22(1): 7-12. doi: 10.1007/s10548-009-0079-4.

[11] NAM H, YIM TG, HAN SK,. Independent component analysis of ictal EEG in medial temporal lobe epilepsy[J]., 2002, 43(2): 160-164. doi: 10.1046/j.1528-1157. 2002.23501.x.

[12] GAO J F, ZHENG C X, and WANG P. Online removal of muscle artifact from electroencephalogram signals based on canonical correlation analysis[J]., 2010, 41(1): 53-59. doi: 10.1177/155005941 004100111.

[13] MOWLA M R, NG S C, ZILANY M S A,. Artifacts-matched blind source separation and wavelet transform for multichannel EEG denoising[J]., 2015, 22: 111-118. doi: 10.1016/j.bspc.2015.06.009.

[14] VERGULT A, DE CLERCQ W, PALMINI A,. Improving the interpretation of ictal scalp EEG: BSSCCA algorithm for muscle artifact removal[J]., 2007, 48(5): 950-958. doi: 10.1111/j.1528-1167.2007.01031.x.

[15] VOS D M, RIES S, VANDEPERREN K,. Removal of muscle artifacts from EEG recordings of spoken language production[J]., 2010, 8(2): 135-150. doi: 10.1007/s12021-010-9071-0.

[16] CHEN X, LIU AP, PENG H,. A preliminary study of muscular artifacts cancellation in single-channel EEG[J]., 14(10): 18370-18389. doi: 10.3390/s141018370.

[17] ANDERSON M, ADALI T, and LI X L. Joint blind source separation with multivariate Gaussian model: Algorithms and performance analysis[J]., 2012, 60(4): 1672-1683. doi: 10.1109/TSP.2011. 2181836.

[18] ANDERSON M, FU GS, PHLYPO R,. Independent vector analysis: Identification conditions and performance bounds[J]., 2014, 62(17): 4399-4410. doi: 10.1109/TSP.2014.2333554.

[19] BELOUCHRANI A, ABED-MERAIM K, CARDOSO J F,. A blind source separation technique using second order statistics[J]., 1997, 45(2): 434-444. doi: 10.1109/78.554307.

[20] CARDOSO J F. High-order contrasts for independent component analysis[J]., 1999, 11(1): 157-192. doi: 10.1162/089976699300016863.

[21] HOTELLING H. Relations between two sets of variates[J]., 1936, 28: 321-377. doi: 10.2307/2333955.

[22] LIN Z L, ZHANG C S, WU W,. Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs[J]., 2006, 53(12): 2610-2614. doi: 10.1109/TBME.2006.886577.

[23] GOLDBERGER A L, AMARAL L A N, GLASS L,. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals[J]., 2000, 101(23): e215-e220. doi: 10.1161/01.CIR. 101.23.e215.

Removal of Muscle Artifact from EEG Data Based on Independent Vector Analysis

CHEN Qiang①CHEN Xun①YU Fengqiong②

①(,,230009,)②(,,230032,)

ElectroEncephaloGram (EEG) data are often contaminated by various electrophysiological artifacts. Among all these artifacts, removing the ones related to muscle activity is particularly challenging. In past studies, Independent Component Analysis (ICA) and Canonical Correlation Analysis (CCA), as Blind Source Separation (BSS) methods, are widely used. In this work, a new method for muscle artifact removal in EEG data using Independent Vector Analysis (IVA) is proposed. IVA utilizes both the higher-order and second-order statistics, so that it makes full use of non-Gaussianity and weak autocorrelation of the muscle artifact and has the advantages of both ICA and CCA. The proposed method is examined on a number of simulated data sets and is shown to have better performance than ICA and CCA. The proposed IVA method is able to largely suppress muscle activity and meanwhile well preserve the underlying EEG activity.

ElectroEncephaloGram (EEG); Muscle artifact; Blind Source Separation (BSS); Independent Vector Analysis (IVA)

TP391; R741.044

A

1009-5896(2016)11-2840-08

10.11999/JEIT160209

2016-03-07；改回日期：2016-07-18；

2016-09-30

陈勋 xunchen@ece.ubc.ca

国家自然科学基金(61501164, 81571760)

The National Natural Science Foundation of China (61501164, 81571760)

陈 强： 男，1972年生，讲师，研究方向为生物医学信号处理.

陈 勋： 男，1987年生，教授，研究方向为生物医学信号处理.

余凤琼： 女，1983年生，讲师，研究方向为神经心理学.