一种基于低秩表示的子空间聚类改进算法
2016-10-13唐振民吕建勇
张 涛 唐振民 吕建勇
一种基于低秩表示的子空间聚类改进算法
张 涛*唐振民 吕建勇
(南京理工大学计算机科学与工程学院 南京 210094)
该文针对现有的基于低秩表示的子空间聚类算法使用核范数来代替秩函数,不能有效地估计矩阵的秩和对高斯噪声敏感的缺陷,提出一种改进的算法,旨在提高算法准确率的同时,保持其在高斯噪声下的稳定性。在构建目标函数时,使用系数矩阵的核范数和Forbenius范数作为正则项,对系数矩阵的奇异值进行强凸的正则化后,采用非精确的增广拉格朗日乘子方法求解,最后对求得的系数矩阵进行后处理得到亲和矩阵,并采用经典的谱聚类方法进行聚类。在人工数据集、Extended Yale B数据库和PIE数据库上同流行的子空间聚类算法的实验对比证明了所提改进算法的有效性和对高斯噪声的鲁棒性。
子空间聚类;低秩表示;秩函数;Forbenius范数;增广拉格朗日乘子法
1 引言
近年来,子空间聚类成为计算机视觉、图像处理、系统辨识等领域的研究热点[1]。基于子空间聚类的算法在处理高维数据时,通常假设高维数据分布于一个联合的低维子空间中,算法根据不同类或类别将高维数据点分割到对应的子空间。常用的子空间聚类算法可以分为4类:迭代方法、代数方法、统计方法和基于谱聚类的方法[2]。
基于谱聚类的方法易于实现并且在实际应用中表现得更好,是目前子空间聚类算法的重点研究方向。基于谱聚类的方法通过探索数据点间的相似性构建亲和矩阵,然后使用谱聚类的方法对亲和矩阵进行聚类。根据稀疏和低秩恢复算法的最新进展,文献[3-6]提出了稀疏子空间聚类算法(Sparse Subspace Clustering, SSC),低秩子空间聚类算法(Low Rank Subspace Clustering, LRSC),低秩表示算法(Low Rank Representation, LRR),通过寻找数据在自身数据字典上的稀疏或者低秩表示来求得亲和矩阵,与其他最先进的子空间聚类算法相比,基于稀疏和低秩表示的方法可以处理噪声和异常值,并且不需要子空间的维数和数目作为先验条件。
LRR将矩阵的秩函数凸松弛为核范数,通过求解核范数最小化问题,求得基于低秩表示的亲和矩阵,在运动分割和人脸聚类等子空间聚类任务中表现出了良好的性能。文献[7]通过对亲和矩阵进行严格的块对角约束提高LRR的性能。文献[8]通过部分的奇异值分解降低LRR的时间复杂度。文献[9]将降低数据的维数和聚类数据到同一子空间整合到同一框架。文献[10]提出了基于拉普拉斯正则化的LRR,同时探索数据的全局结构和局部的流形结构。文献[11]通过对偶图规则化同时保护数据在外围空间和特征空间的几何信息。虽然上述LRR系列的算法大大提高了子空间聚类的性能,但是它们却同时忽略了一个问题,使用核范数代替秩函数是否能准确地估计矩阵的秩,因为核范数的弱凸性,常常导致算法的不稳定和对高斯噪声的敏感。
本文的创新工作在于:(1)受Elastic net[12]思想启发,在构建低秩表示的目标函数时,同时使用系数矩阵的核范数和Forbenius范数代替秩函数,提高算法稳定性并对噪声更加鲁棒;(2)利用非精确的增广拉格朗日乘子方法(Augmented Lagrange Multiplier, ALM)[13]求解最优化问题,对求得的系数矩阵进行后处理得到亲和矩阵,最后采用经典的谱聚类方法[14]进行聚类。本文的内容组织如下:第2节主要介绍了子空间聚类问题和低秩表示算法;第3节详细阐述了本文的改进算法;第4节为实验结果分析;第5节是结论。
2 子空间聚类和低秩表示简介
LRR算法将从单一子空间中恢复低秩矩阵扩展到从多子空间中恢复低秩矩阵,同时聚类数据并且修正稀疏错误。LRR的基本思想是将数据矩阵表示成在字典矩阵下的线性组合,即,并希望线性组合的系数矩阵是最低秩的,LRR的基本模型为:
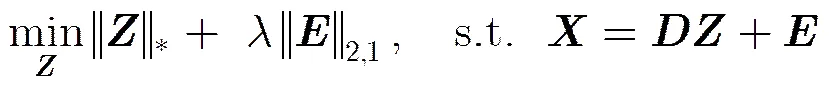
3 Elastic net正则化的低秩表示
本文提出了Elastic net正则化的低秩表示算法(Elastic net Regularized Low Rank Representation, ERLRR),不同于传统的LRR用核范数来估计秩函数,我们联合矩阵的核范数和Forbenius范数作为正则项来估计秩函数。
3.1构建ERLRR算法的目标函数
Elastic net是统计学习中一类有效的模型[12],将范数和范数联合作为惩罚函数,范数保证复杂模型解的稀疏性,范数保证复杂模型解的稳定性,应用于低秩矩阵恢复问题中获得了很好的效果[15]。
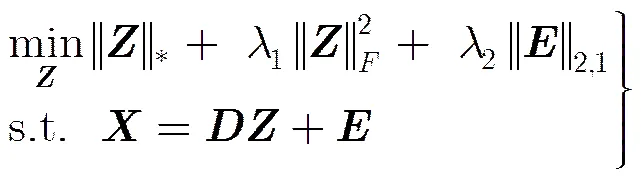
3.2求解ERLRR算法的目标函数
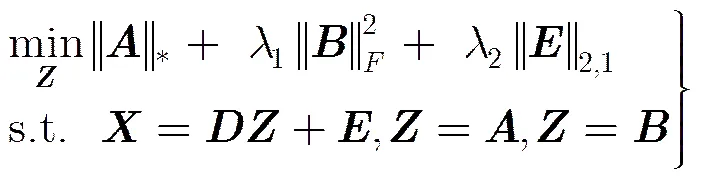
式(3)的增广拉格朗日函数为
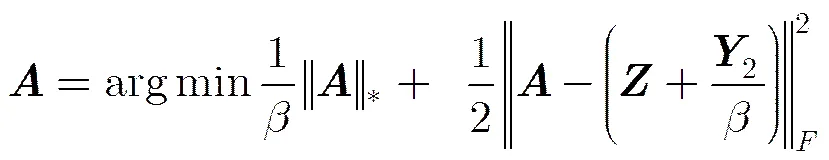
式(5)是凸优化问题并且有闭合解,可以通过奇异值阈值算子[16]求解,其解为,其中和是通过奇异值分解获得的正交矩阵,是收缩阈值算子。
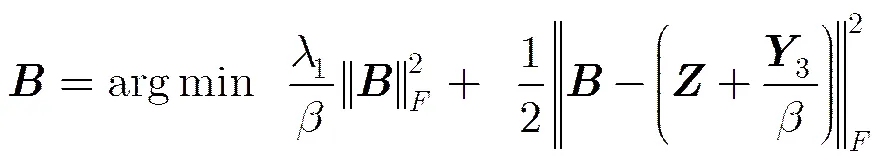
通过对式(7)求偏导得:
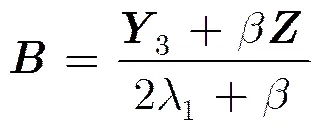
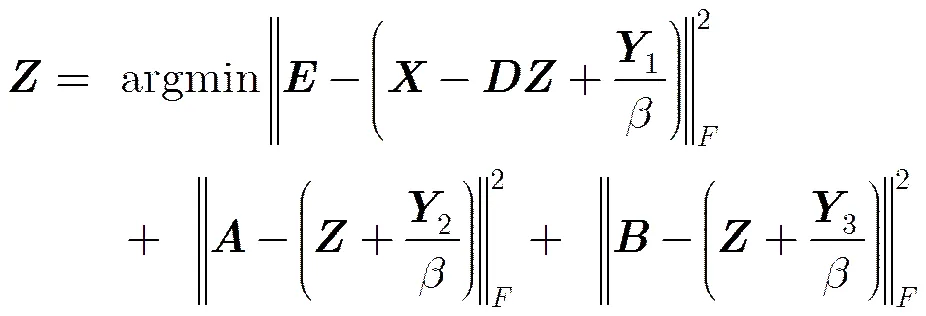
通过对式(9)求偏导得:
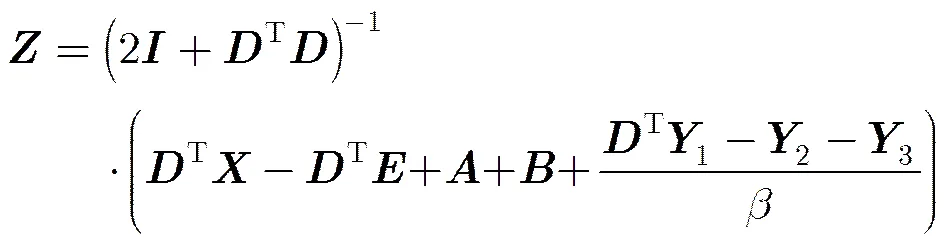
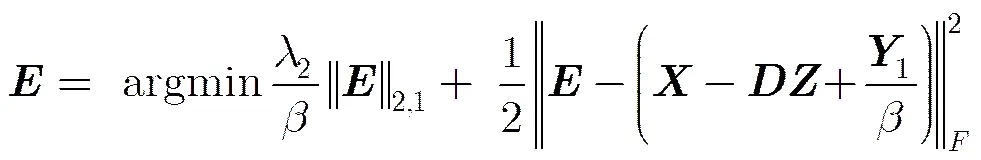
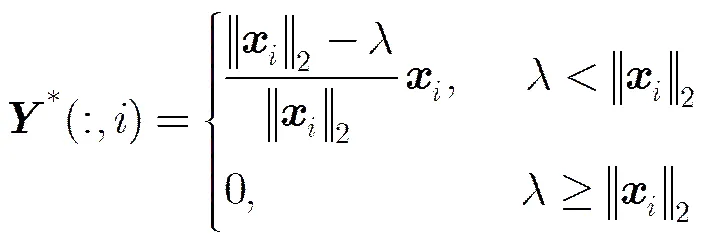
3.3基于ERLRR的子空间聚类
3.4 算法时间复杂度和收敛性
在本小节,我们讨论ELRR算法的时间复杂度和收敛性。通常,算法的主要计算在求解式(5)中,因为该过程包含了矩阵的奇异值分解,当数据样本的数目非常大时,算法变得十分耗时。采用文献[6]的方法,用字典矩阵的正交基来代替,算法的时间复杂度为,其中是字典的秩,为算法的迭代次数,本文我们使用数据矩阵作为字典矩阵,即,当,时间复杂度最多为,当,时间复杂度最多为。
当目标函数平滑时,文献[18]给出了精确的ALM收敛性的一般性证明。非精确的ALM作为精确的ALM的变形,当有两个变量矩阵交替迭代时,算法的收敛性已经得到证明[19]。然而,求解LRR系列算法时,非精确的ALM通常包括两个以上的变量矩阵交替迭代(LRR包括3个迭代的变量矩阵,和, ERLRR包括4个迭代的变量矩阵,,和),这种情况下算法的收敛性很难在理论上证明[6]。但是通过多次实验证明,非精确的ALM在最优化问题中通常都能很好地收敛。
4 实验结果与分析
在本节,将本文提出的ERLRR算法与局部子空间亲和(Local Subspace Afffinity, LSA)[20],谱曲率聚类(Spectral Curvature Clustering, SCC)[21],最小二乘回归(Least Squares Regression, LSR)[22], SSC[3], LRSC[4]和LRR[6]这些基于谱聚类的流行算法在人工数据集、Extended Yale B数据库和PIE数据库上进行对比试验。本文实验环境为Intel酷睿i7 4710MQCPU, 8G内存的联想Y430P笔记本电脑。
4.1人工数据集
本文创建一个人工数据集用来比较不同算法的性能。类似于文献[5]和文献[10],我们建立5个独立的子空间,它们的基通过计算,其中是一个随机矩阵,是一个维数为20010的随机正交矩阵。所以,每个子空间的维数为10,外围空间的维数为200。我们通过从每个子空间选取100个数据向量,其中是10100的矩阵,矩阵中的每个元素是之间均匀分布的随机数。在产生的数据矩阵中随机选取20%的数据向量加入均值为0,方差为的高斯噪声,其中是选取的数据向量。表1为各算法在该人工数据集上的结果。由表1可知,本文的ERLRR的聚类错误最小,表现出了最好的性能。
LSR, LRSC, LRR, SSC与本文方法都是通过构建亲和矩阵,然后将亲和矩阵应用于NCuts等谱聚类方法进行数据聚类,优秀的亲和矩阵可以使算法获得更好的性能,图1显示了上述算法求得的亲和矩阵。通过综合比较,可以看出ERLRR亲和矩阵的块对角比较明显,毛刺非常少,这是因为ERLRR目标函数中加入了正则项,保持了算法的稳定性,去除了高斯噪声的干扰。
4.2 Extended Yale B数据库
Extended Yale B数据库是测试子空间聚类算法的标准数据库,我们将原数据库的192168像素的图像下采样到4842像素,使用2016维矢量化的图像作为一个数据样本。我们按照文献[3]的实验设置,将38类图像分为4组,1到4组分别有类别1~10, 11~20, 21~30和31~38,对于前3组中的每一组,我们的实验使用所有可选的2,3,5,8,10个类别,对于第4组,我们使用所有可选的2,3,5,8个类别进行重复实验,通过搜索选取各算法的最优参数,实验的结果如表2所示。
表2说明了在不同的聚类类别下,ERLRR都获得了更低的聚类错误。LRR和SSC作为流行的基于低秩表示和稀疏表示的子空间聚类算法,也获得了比较低的聚类错误。LRSC在低秩表示的模型中尝试恢复没有错误的数据,但是没有对求得的系数矩阵进行进一步后处理,它的聚类错误要高于LRR。因为LSR是基于均方误差(Mean Square Erroes, MSE)的算法,MSE对远离其他数据点的异常值很敏感,而Extended Yale B数据库有较多的光照非常暗或者非常亮的图像,所以LSR的聚类错误也更高。LSA和SCC尝试探索数据的局部和全局结构来获得亲和矩阵,但是这两个算法没有明确地处理受损的数据,在有复杂噪声的数据库上,它们表现出了最差的性能。
事实上,高斯噪声是一种常见的噪声,图像经常会被其干扰,我们选取数据库的前10类共640张图像测试算法在高斯噪声干扰下的稳定性。实际应用中,我们并不知道受高斯噪声干扰图像的数目,更无法针对不同的干扰情况搜索合适的算法参数。在本节实验中,我们保持各算法的参数不变,分别随机选取20%, 60%, 100%的图像加入均值为0,方差为0.01的高斯噪声,表3显示了算法的聚类错误。
表1各算法在人工数据集上的结果(%)

错误率算法 LSASCCLSRLRSCLRRSSCERLRR 15.230.415.29.215.215.20.8
表2各算法在Extended Yale B数据库上的平均聚类错误(%)
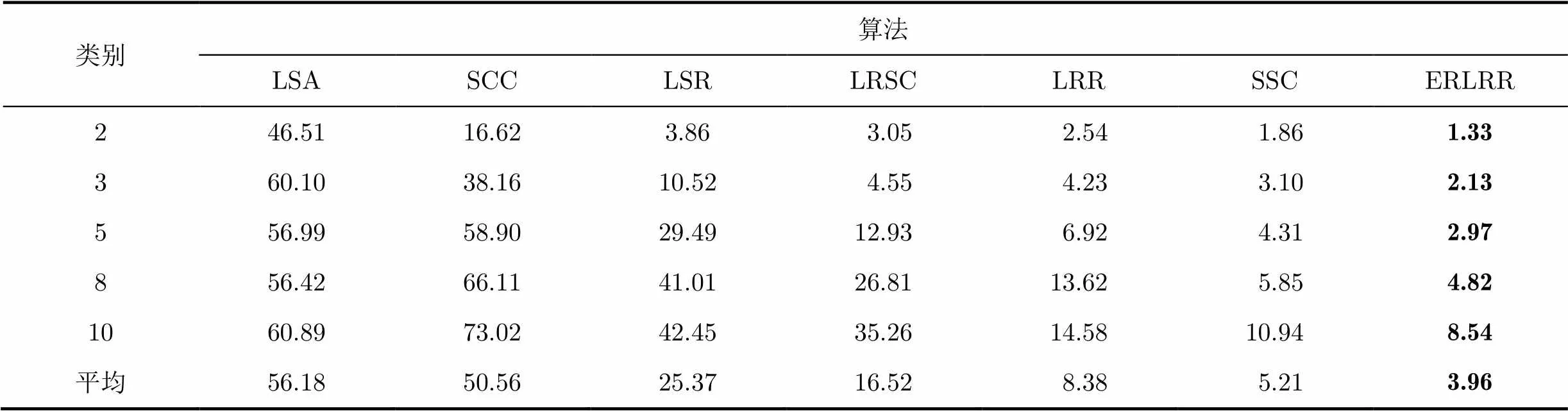
类别算法 LSASCCLSRLRSCLRRSSCERLRR 246.5116.623.86 3.05 2.54 1.861.33 360.1038.1610.52 4.55 4.23 3.102.13 556.9958.9029.4912.93 6.92 4.312.97 856.4266.1141.0126.8113.62 5.854.82 1060.8973.0242.4535.2614.5810.948.54 平均56.1850.5625.3716.52 8.38 5.213.96

图1 各算法的亲和矩阵
表3各算法在均值为0,方差为0.01的高斯噪声下的聚类错误(%)

比率(%)算法 LSASCCLSRLRSCLRRSSCERLRR 2062.1971.4143.2838.4423.2829.22 7.03 6067.1978.9141.5637.5026.0940.16 8.91 10077.8181.5640.3137.8139.8451.7218.59 平均69.0677.2941.7237.9229.7440.3711.51
在比较的算法中,ERLRR获得了最好的效果,说明ERLRR算法中对高斯噪声更加鲁棒。LRR和SSC随着高斯噪声图像的增多,聚类错误也变得更高,其中SSC相比于没有高斯噪声的情况,算法性能下降的十分明显。在该数据库上,LRSC和LSR受高斯噪声干扰较小,聚类错误变化并没有随着高斯噪声图像的增多而增加,但都高于ERLRR。LSA和SCC在高斯噪声情况下,依然表现出了最差的性能。
4.3 PIE数据库
PIE数据库是一个有代表性的人脸图像数据库,广泛地应用于聚类实验。该数据库包含了68类在不同姿态、光照和表情下的人脸图像。在本节实验中,我们选取该数据库的子集(作者提供的Matlab文件Pose05_68_49_64_64.mat)共3332张图片进行实验。我们从数据中随机选取2,3,5,8,10个类别进行聚类实验,重复实验20次,通过搜索选取各算法的最优参数,平均的聚类错误如表4所示。
在该数据库上,除了LSA和SCC因为模型的局限性,聚类错误依然很高,其他算法的性能相近。SSC在聚类类别较小时,表现出了非常优秀的性能,但随着聚类类别的增加,错误率要高于ERLRR。我们观察到LRR在该数据库上的错误率高于LRSC和LSR,这不同于在Extended Yale B数据库上的结果,说明虽然选取了最优参数,但是LRR模型在不同数据库上不够稳定。作为LRR的改进算法,本文提出的ERLRR在不同类别的情况下错误率均低于LRR,并且平均的聚类错误低于其他算法,说明ERLRR提高了LRR的准确性和稳定性。
为了测试高斯噪声在该数据库上对各算法的影响,我们选取数据库的前10类共490张图像进行实验,仍然保持各算法的参数不变,分别随机选取20%, 60%, 100%的图像加入均值为0,方差为0.5的高斯噪声,相比于4.2节,我们加强了噪声强度,表5显示了算法的聚类错误。
由表5可知,在不同的高斯噪声下,ERLRR的性能均优于其他算法,平均聚类错误比LRR低了17.62%。各算法在该数据库上并没有随着高斯噪声图像的增加,聚类错误也随之增加的规律,说明各算法受高斯噪声的影响而不够稳定。事实上,给数据加入方差较小的噪声,对各算法的聚类错误影响较小,如果加入方差较大的噪声,图像变形严重,各算法包括本文算法都变得不稳定,难以获得较好的聚类性能。
表4各算法在PIE数据库上的平均聚类错误(%)
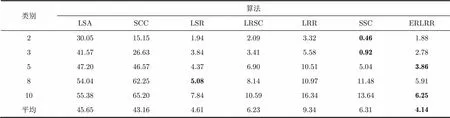
类别算法 LSASCCLSRLRSCLRRSSCERLRR 230.0515.151.942.093.320.461.88 341.5726.633.843.415.580.922.78 547.2046.574.376.9010.515.043.86 854.0462.255.088.1410.9711.485.91 1055.3865.207.8410.5916.3413.646.25 平均45.6543.164.616.239.346.314.14
表5各算法在均值为0,方差为0.5的高斯噪声下的聚类错误(%)

比率(%)算法 LSASCCLSRLRSCLRRSSCERLRR 2061.6370.6119.7911.8418.3734.086.53 6071.8476.1246.7411.6325.7132.457.96 10067.1476.9440.8225.3140.8222.2517.55 平均66.8774.5735.7816.2628.3029.5910.68
4.4 参数选择
我们分别在Extended Yale B数据库和PIE数据库聚类类别为10的情况下进行实验,分析参数选择对ERLRR算法的影响。ERLRR算法需要确定模型中的参数和,取值为,取值为,通过搜索不同参数值对实验结果的影响进行评估。图2表明当变化时对聚类错误的影响,图3表明当取实验效果最优的条件下,搜索不同值对聚类错误的影响。由图2,图3可知,时,ERLRR的聚类错误最低。由于不同的数据库受噪声影响程度不同,平衡噪声项的的最优值也不同。
5 结束语
根据Elastic net的基本思想,本文提出一种基于低秩表示的子空间聚类改进算法ERLRR。不同于传统的LRR算法,ERLRR联合矩阵的核范数和Forbenius范数作为正则项来估计秩函数,提高了算法的稳定性。然后我们采用非精确的ALM求解最优化问题,对求得的系数矩阵进行后处理得到亲和矩阵,最后采用经典的谱聚类方法进行聚类。在人工数据集、Extended Yale B数据库和PIE数据库上同流行的子空间聚类算法进行实验对比,证明了ERLRR算法的聚类性能更加优秀并且对高斯噪声更加鲁棒。下一步,我们将会融合ERLRR算法和基于流形正则化的LRR算法,同时探索数据的全局结构和局部结构,进一步提高子空间聚类算法的性能。同时,如何自适应地选择模型参数也是今后研究的重点方向之一。
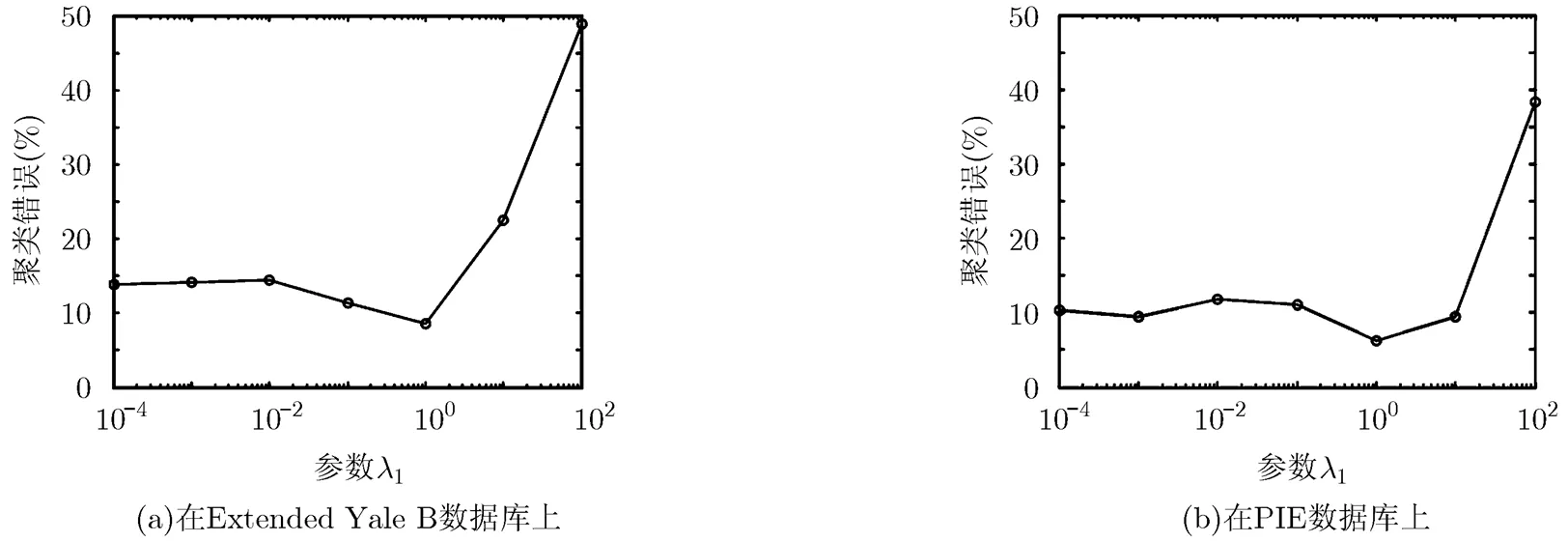
图2 参数对聚类错误的影响
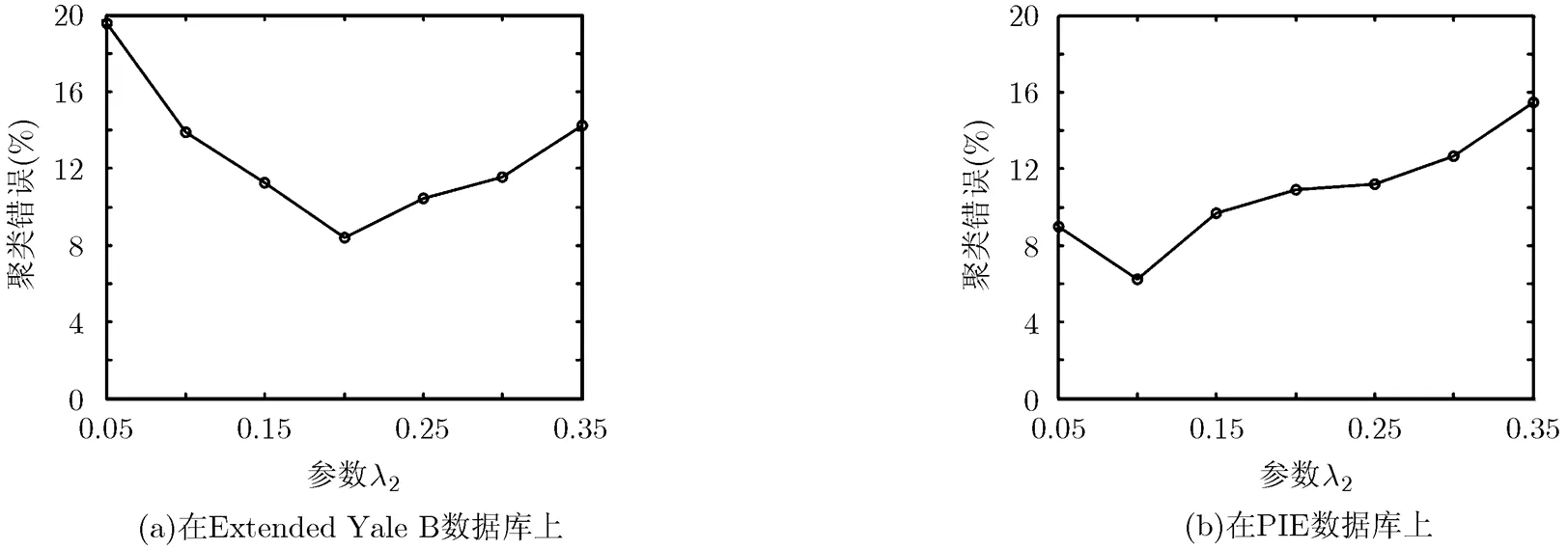
图3 参数对聚类错误的影响
[1] 王卫卫, 李小平, 冯象初, 等.稀疏子空间聚类综述[J]. 自动化学报, 2015, 41(8): 1373-1384. doi: 10.16383/j.aas.2015. c140891.
WANG Weiwei, LI Xiaoping, FENG Xiangchu,. A survey on sparse subspace clustering[J].2015, 41(8): 1373-1384. doi: 10.16383/j.aas.2015.c140891.
[2] VIDAL R. Subspace clustering[J].2011, 28(2): 52-68. doi: 10.1109/MSP.2010.939739.
[3] ELHAMIFAR E and VIDAL R. Sparse subspace clustering: Algorithm, theory, and applications[J]., 2013, 34(11): 2765-2781. doi: 10.1109/TPAMI.2013.57.
五、投喂管理。苗种投放后第二天便可投饵,将饵料投放在食台上,开始少投,吸引甲鱼前来摄食,每天投喂2次,上午8-9时,下午5-6时,投饵量为甲鱼总重2%~3%,每天观察甲鱼的摄食情况,适时调整投饵量,在制作饵料时可加入3%左右植物油,既可增强甲鱼的食欲,又可提高饵料中蛋白质的利用率。
[4] VIDAL R and FAVARO P. Low rank subspace clustering (LRSC)[J]., 2014, 43: 47-61. doi: 10.1016/j.patrec.2013.08.006.
[5] LIU G C, LIN Z C, and YU Y. Robust subspace segmentation by low-rank representation[C]. Proceedings of the International Conference on Machine Learning, Haifa, Israel, 2010: 663-670.
[6] LIU G C, LIN Z C, YAN S C,. Robust recovery of subspace structures by low-rank representation[J].2013, 35(1): 171-184. doi: 10.1109/TPAMI.2012.88.
[7] FENG J S, LIN Z C, XU H,. Robust subspace segmentation with block-diagonal prior[C]. Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 3818-3825. doi: 10.1109/CVPR.2014.482.
[8] ZHANG X, SUN F, LIU G C,. Fast low-rank subspace segmentation[J]., 2014, 26(5): 1293-1297. doi: 10.1109/TKDE. 2013.114.
[9] PATEL V M, NGUYEN H V, and VIDAL R. Latent space sparse and low-rank subspace clustering[J]., 2015, 9(4): 691-701. doi: 10.1109/JSTSP.2015.2402643.
[10] LIU J M, CHEN Y J, ZHANG J S,. Enhancing low-rank subspace clustering by manifold regularization[J]., 2014, 23(9): 4022-4030. doi: 10.1109/TIP.2014.2343458.
[11] YIN M, GAO J B, LIN Z C,. Dual graph regularized latent low-rank representation for subspace clustering[J]., 2015, 24(12): 4918-4933. doi: 10.1109/TIP.2015.2472277.
[12] MOL C D, VITO E D, and ROSASCO L. Elastic- net regularization in learning theory[J]., 2009, 25(2): 201-230. doi: 10.1016/j.jco.2009. 01.002.
[13] LIN Z C, CHEN M M, and MA Y. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[R]. UIUC Technical Report UILU-ENG-09-2215, 2009.
[14] NG A Y, JORDAN M, and WEISS Y. On spectral clustering: Analysis and an algorithm[C]. Proceedings of the Advances in Neural Information Processing Systems, Vancouver, Canada, 2001: 849-856.
[15] LI H, CHEN N, and LI L Q. Error analysis for matrix elastic-net regularization algorithms[J]., 2012, 23(5): 737-748. doi: 10.1109/TNNLS.2012.2188906.
[16] CAI J F, CANDES E J, and SHEN Z W. A singular value thresholding algorithm for matrix completion[J]., 2010, 20(4): 1956-1982. doi: 10.1137/080738970.
[17] SHI J B and MALIK J. Normalized cuts and image segmentation[J]., 2000, 22(8): 888-905. doi: 10.1109/ 34.868688.
[18] BERTSEKAS D. Constrained Optimization and Lagrange Multiplier Methods[M]. Belmont, MA, USA: Athena Scientific, 1996: 326-340.
[19] CANDES E J, LI X D, MA Y,. Robust principal component analysis[J]., 2010, 58(1): 1-37. doi: 10.1145/1970392.1970395.
[20] YAN J Y and POLLEFEYS M. A general framework for motion segmentation: Independent, articulated, rigid, non-rigid, degenerate and non-degenerate[C]. Proceedings of the European Conference on Computer Vision, Graz, Austria, 2006: 94-106. doi: 10.1007/11744085_8.
[21] CHEN J L and LERMAN G. Spectral curvature clustering (SCC)[J]., 2009, 81(3): 317-330. doi: 10.1007/s11263-008-0178-9.
[22] LU C Y, MIN H, ZHAO Z Q,. Robust and efficient subspace segmentation via least squares regression[C]. Proceedings of the European Conference on Computer Vision, Florence, Italy, 2012: 347-360. doi: 10.1007/978-3-642- 33786-4_26.
Improved Algorithm Based on Low Rank Representationfor Subspace Clustering
ZHANG Tao TANG Zhenmin LÜ Jianyong
(,,210094,)
The nuclear norm is used to replace the rank function in the subspace clustering algorithm based on low rank representation, it can not estimate the rank of the matrix effectively and it is sensitive to Gauss noise. In this paper, a novel algorithm is proposed to improve the accuracy and maintain its stability under the Gauss noise. When building the objective function, the nuclear norm and Forbenius norm of coefficient matrix are used as the regularizationterms, after a strong convex regularizer over singular values of coefficient matrix, an inexact augmented Lagrange multiplier method is utilized to solve the problem. Finally, the affinity matrix is acquired by post-processing of coefficient matrix and the classical spectral clustering method is employed to clustering. The experimental comparison results between the state-of-the-art algorithms on synthetic data, Extended Yale B and PIE datasets demonstrate the effectiveness of the proposed improved method and the robustness to Gauss noise.
Subspace clustering; Low rank representation; Rank function; Forbenius norm; Augmented Lagrange multiplier method
TP391
A
1009-5896(2016)11-2811-08
10.11999/JEIT160009
2016-01-04;改回日期:2016-05-12;
2016-07-19
张涛 njustztwork@126.com
国家自然科学基金(61473154)
The National Natural Science Foundation of China (61473154)
张 涛: 男,1987年生,博士生,研究方向为图像处理、模式识别.
唐振民: 男,1961年生,教授,博士生导师,研究方向为图像处理、智能机器人与智能检测.
吕建勇: 男,1979年生,讲师,研究方向为图像处理、计算机视觉.
