线性代数中矩阵章节基本概念及性质的教学方法探讨
2016-10-13姜爱平
姜爱平
线性代数中矩阵章节基本概念及性质的教学方法探讨
姜爱平
(宁夏大学 数学计算机学院,宁夏 银川 750021)
线性代数中矩阵章节的基本概念及性质较多且抽象,而基本概念及性质的理解直接影响学生对本课程知识的掌握和学习兴趣.结合教学实践,从注重基本概念的应用背景、重视基本概念在学科发展中的作用等方面将枯燥抽象的基本概念化为具体生动的问题,这对激发学生的求知欲,培养学生思维的逻辑性和严谨性,提高其实践创新能力具有一定意义.
线性代数;矩阵;基本概念
线性代数是很多高校理工科、经管和农林等专业开设的一门公共基础课,该课程基本概念较多且抽象,知识具有较强的连贯性,这对大多数非数学专业的学生而言,普遍感到学习较困难,学习兴趣下降.另外,各高校进行的教育教学改革,使得理论学时由64学时减少为32学时,这使得教学质量难以保障[1-2].线性代数这门课程主要借助行列式和矩阵等工具研究线性空间的结构和性质,因此,矩阵章节知识点的掌握好坏,对后续知识的学习和理解至关重要.本文结合教学实践,针对矩阵章节重要基本概念及性质的教学方法,从注重基本概念的背景知识,重视基本概念在学科发展中的作用等方面进行探讨,以期将枯燥抽象的数学概念转化为生动具体的实际问题,既激发学生的学习兴趣,又提高学生的数学应用能力和创新实践能力.
1注重基本概念的应用背景
线性代数课程中矩阵章节的一些基本概念有很强的实际应用背景,若在讲授这些基本概念之前,能从实际问题出发,通过归纳总结,提炼成数学问题,进而解决问题,并应用到实际生活当中,这将对激发学生学习兴趣,提高课堂教学效果,培养学生实践创新能力等有很大帮助.
例1[3]假定某地区人口总数保持不变,每年有5%的农村人口流入城镇,有1%的城镇人口流入农村,求年后该地区的城镇人口与农村人口的比例,分析最终是否会趋于一个稳定状态.
例2[4]在通信或信号处理等相关领域,若规定1~26个数字与26个英文字母一一对应,假设密钥矩阵,已知接收信号为,求发出信号.
2重视基本概念在学科发展中的作用
任何一个学科的诞生和发展都离不开现实问题的出现和解决.因此,教师在授课之前应引导学生多思考,理清为什么要学习这个概念,有什么问题需要解决,怎么解决等.将知识转化为思考,让学生参与进来,体会到思考和学习带来的快乐,感受到学科发展的曲折,如此,方能达到教书育人的目的.如在学习行列式的定义之前,通过观察二元一次线性方程组其解的表达式,发现其结构复杂且具有一定的规律和特点,自然就会想到,若规定,则该方程组其解的表达式大为简化,即,,其中:为线性方程组系数所构成的二阶行列式,为中第列被常数项代替后形成的行列式.以此类推,可以给出三阶行列式的定义.针对四阶行列式的展开式项数的猜想,有2种不同的答案,即根据对角线法则得出的8项和观察二阶、三阶行列式的展开式得出的4!项.针对这个问题,依然可以通过解四元一次线性方程组,观察其解的结构,得出四阶行列式的展开式应该是项.当然,也可以通过逆序数和全排列等知识,得出同样的结论.
对于矩阵的秩等基本概念的学习,课堂上教师可以设问几个问题,如为什么要学习这个概念,哪些问题需要解决等.实际上,对于元一次线性方程组,克拉默法则仅适用于方程个数等于未知元个数,且系数行列式时线性方程组解的判定,然而对于当系数行列式情况和方程个数不等于未知元个数时方程组解的判定等问题尚不清楚.同时,若矩阵,则相互等价,即它们的行阶梯形矩阵非零行的行数是唯一不变的,这个参数其实就反映了矩阵的本质属性,就是后面要学习矩阵的秩这个概念.实际上,即使学习了矩阵的秩,掌握了线性方程组解的判定定理后,当方程组有无穷多解时,各个解之间的关系以及解的结构是什么等问题仍不清楚,这就是需要学习向量组这一章的原因.所以,课堂上,尤其是在学习新的概念和定义之前,授课教师应该循循善诱,因势利导,让学生了解到学科知识的来龙去脉,前因后果,这在培养学生思维的逻辑性和知识的系统性等方面可起到事半功倍的效果.
3多角度深化基本概念及性质
对于教材上的定义和性质,可从不同角度举一反三,深化知识,开阔思路,最终学以致用.如二阶行列式可看成是由其列元素为向量坐标的2个向量所张成的平行四边形的面积,三阶行列式可看成由其列元素作为向量坐标的3个向量张成的平行六面体的体积,依次类推,阶行列式可看成是由个向量张成的维平行多面体的体积[5];文献[6]中有关于施密特正交化(schimidt)数学公式,即
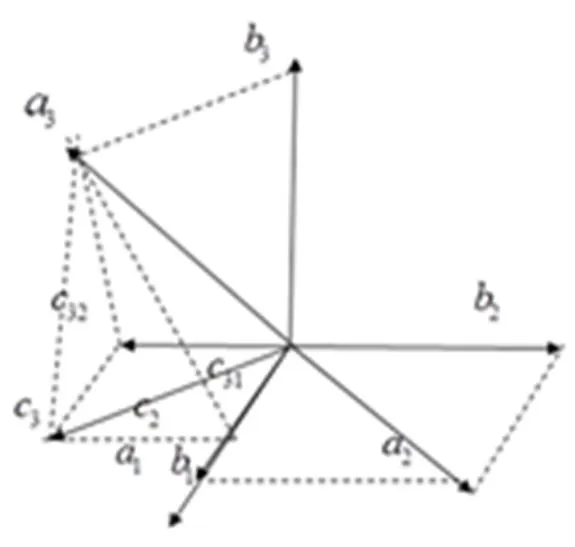
图1 施密特正交化的几何解释
另外,对矩阵特征值和特征向量的定义也可进一步地深入学习,由可知,若为实数,表明非零向量在变换的作用下伸长或者压缩,方向相反或者相同;若为复数,即,则表明非零向量在变换的作用下伸长倍,同时旋转角度.
除了从几何角度进行研究外,一一对应的思想也可以辅助理解新的性质,如矩阵与线性变换一一对应,可通过分析研究线性变换所具有的性质,来达到研究对应矩阵的目的.
4重视基本概念中的“同”和“异”
类比归纳是一种常见的数学思想方法,通过比较发现2种不同属性事物的“同”和“异”,对于相同之处,进行归纳总结,提炼形成抽象理论,对于“不同”之处,则分析研究其具体原因.通过长期的思维训练,相信这对深入理解基本概念及其性质,培养学生思维的严谨性具有很好的帮助作用[7-8].如行列式的加法运算与矩阵的加法运算的“同”与“异”,相同之处是均为实数的加法运算,不同之处在于前者仅对同一行(列)元素加法运算,其他行(列)元素保持不变,而后者是对同型矩阵所有元素均进行加法运算;行列式的数乘运算与矩阵的数乘运算的“同”与“异”,相同之处是书写形式相同,不同之处在于行列式的数乘仅仅是对某一行(列)元素乘以该常数,而矩阵的数乘表示所有元素均乘以该常数;实数运算所满足的运算规律(如交换律,结合律和分配律)与矩阵运算满足运算律(结合律和分配律)之间的“同”与“异”;矩阵乘积的转置运算与矩阵乘积的逆运算
5注重基本概念的归纳和推广
在学习矩阵的线性运算、乘法运算和转置运算后,同济大学编著的《线性代数》[6]在后续章节介绍了伴随矩阵、方阵的行列式、逆矩阵以及矩阵的初等变换等基本概念,实际上伴随矩阵、方阵的行列式、逆矩阵、矩阵的初等变换以及矩阵对角化等都可以理解为矩阵的运算.由其运算结果可知,矩阵运算结果可以是数(如行矩阵左乘列矩阵、方阵的行列式),也可以是矩阵.矩阵的秩与向量组的秩(或最大无关组所含向量的个数)、解空间的基础解系所含向量的个数以及向量空间的维数等概念之间的关系,实际上属于层层递推,是概念的延伸和推广.除此之外,由线性方程组解的判定定义也可直接推广得到向量由向量组线性表示的判定定理.所以,教师在讲授新概念的同时,若注重知识的连贯和衔接以及概念的外延,从某种程度上能有效地提高课堂效果,保障教学质量.
线性代数课程主要内容是借助行列式和矩阵等工具研究线性方程组解空间的结构,探讨线性空间及线性变换等基本性质.而矩阵章节所涉及的基本概念和性质多且抽象,学生不易理解.为此,本文结合教学实践,通过注重基本概念的应用背景,重视基本概念在学科发展中的作用,多角度深化基本概念及性质,重视基本概念中的“同”和“异”,注重基本概念的归纳和推广等5个方面重视基本概念及其性质的课堂讲授和练习,这对提高学生学习兴趣,激发求知欲,完善知识结构,培养学生的实践创新能力具有一定的实际意义.
[1] 王建鹏,马会礼.工科线性代数课程教学改革研究[J].高师理科学刊,2015,35(1):71-73
[2] 孙春涛,蹇红.关于线性代数课程教学方法的探讨[J].教育教学论坛,2014(22):70-71
[3] 李秀兰,张红玉.线性代数在数学建模中的应用[J].山西大同大学学报:自然科学版,2010,26(4):3-4
[4] 孙延修.线性代数教学方法的思考与探索[J].高师理科学刊,2013,33(5):103-105
[5] 陈佘喜.加强线性代数教学,提高学生的数学能力[J].当代教育理论与实践,2013,5(4):109-111
[6] 同济大学数学系.工程数学·线性代数[M].5版.北京:高等教育出版社,2007
[7] 张莉,周羚君.类比方法在线性代数教学中的应用[J].大学数学,2014,30(6):67-69
[8] 李俊华,陈艳菊.浅谈数学思想在线性代数概念教学中的应用[J].教育教学论坛,2015(10):181-182
Research on the teaching method of the definition and properties about the matrix in linear algebra
JIANG Ai-ping
(School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China)
The basic concepts and properties about the matrix in linear algebra are more abstract,which directly affect students to master this course knowledge and interest in learning.Try to change the abstract concept into specific problem in the way of paying attention to the application background of the concept,the role of concept in the subject development,etc.Which is interesting for stimulating students′ thirst for knowledge,training logical thinking and improving the practice innovation ability.
linear algebra;matrix;basic concept
O151.2∶G642.0
A
10.3969/j.issn.1007-9831.2016.03.014
2015-11-01
宁夏大学教育教改项目
姜爱平(1981-),女,河南漯河人,副教授,硕士,从事灰色系统理论研究.E-mail:jiangaiping2000@126.com
