基于高维度特征分析的非局部图像质量评价方法

丁 勇 李 楠



基于高维度特征分析的非局部图像质量评价方法

丁 勇 李 楠*

(浙江大学超大规模集成电路设计研究所 杭州 310027)

传统的图像质量评价方法通常提取低维度特征即图像的片面信息用来分析图像质量。高维度特征尽管不易分析但保留了更多信息，更利于全面分析图像质量。针对这种现状，该文提出一种优化数据采样后基于高维度特征分析的图像质量评价方法。首先对图像数据采样分别利用块匹配进行筛选，用主成分分析进行降维，其次利用核独立分量分析从图像数据采样中提取高维度特征，最后基于自然图像统计特性对特征进行综合得出图像质量。实验结果表明所提方法与人的主观评价较为一致。

图像质量评价；高维度特征；非局部；核独立分量分析

1 引言

图像质量是图像处理系统中重要的反馈参数[1]。随着多媒体和互联网技术的发展，图像和视频在编码，压缩和传输过程中引入的失真使得图像质量评价的重要性日益提高。相对于主观图像质量评价的耗时，不可重复且昂贵的特点，客观图像质量评价若能设计出与人的主观评价相一致的算法，则能够大大降低图像质量评价成本，具有巨大的研究和应用价值。

从原始图像可以提供的信息量进行分类，客观图像质量评价可以分为全参考，半参考和无参考3类[2]。从提取的特征进行分类，客观图像质量评价可以分为基于误差，基于人眼视觉特性和基于自然图像统计3种模型。误差模型将引入的失真作为失真信号，将失真图像作为失真信号与原始信号的简单叠加，得出具有一定物理意义的评价。虽然运算简单且快捷，但是对于非加性的失真，误差模型效果不够理想。视觉特性模型会模拟人眼视觉特性[3]，利用滤波器或者分解方法，提取出对应特征并量化综合得出图像质量。自然图像统计[4]模型认为失真的引入使得图像的统计特性发生了改变，故可据此进行量化综合，得出图像质量。相比误差模型，视觉特性模型和自然图像统计模型更符合人的主观感知。

鉴于对于图像边缘和结构信息的提取较为容易，现有的图像质量评价方法大多基于人眼视觉特性模型。其中，结构相似度(SSIM)[5]结合了亮度，对比度和结构来模拟人眼对于图像最直观的评价。其他一些方法利用小波分解或者Contourlet变换[6]，来模拟人眼的多通道、多尺度或多方向特征。近些年研究者逐渐开展基于自然图像统计模型的研究并取得了一定的成果[7]。其中比较具有代表性的研究利用独立分量分析提取出的分量作为特征，分析统计特性与质量之间的关系[8]。以上的方法虽然能够较有效对图像质量进行评价，但是提取的特征都是简单的线性特征，低维度的特征抛弃了图像的绝大多数信息，只留下相关的片面信息用来分析质量。如果将低维空间映射到高维空间，一些原本不可分的特征在映射后可能可分，尽管不易提取和分析，但是高维特征空间中的特征分量包含更多图片信息，能更好地解释人眼视觉神经的非线性和复杂性，因此更有利于图像质量的评价。

本文介绍了一种基于对高维特征进行统计特性分析的图像质量分析方法。首先利用块匹配方法优化了空域的数据采样产生非局部的采样数据，利用核方法对特征空间进行高维映射，在映射后的空间进行特征提取，最后基于自然图像统计特性对高维度特征进行综合并得出图像质量。

2 数据处理和特征提取

2.1数据筛选

通常情况下图像质量分析的特征提取自大范围的随机采样或者图像分块后的所有数据。随机采样或者小窗口采样过程产生的相似的图像块增加了数据的冗余。冗余可以有两种含义，一种是图像的冗余信息，另一种是数据采样的重复数据。前者对于图像质量的分析是有贡献的，但是后者不能对于图像质量的分析产生叠加的效果。图像数据采样会出现采样结果相同的情况，虽然概率极小但是可能存在，这样产生的冗余数据，更会影响到后续的分量分析，因为独立分量分析问题必须满足数据采样满秩。同时，图像分块的采样方法虽然在数据采样中保留了图像的全部信息，但是产生了局部数据的相关性。本文应用块匹配方法对采样数据进行初步筛选，一定程度去除了局部数据的相关性，使数据采样非局部化，一定程度上去除对图像质量分析无用的冗余数据，以达到优化采样过程的目的。

块匹配常用于视频压缩的运动估计和运动检测中[9]，主要作用是寻找相似的图像块。其基本思想在于将图像分块后，计算各子块和参考块之间的误差，并将误差小于一定阈值的块归为一组。假设图像的任意一参考块为ref，那么块匹配的结果是与参考块的距离小于一定阈值的图像块的集合。

(2)

2.2数据降维

图像的采样数据具有较大的维度，其中也包含了较大的信息量，难以直接利用高维度特征提取出有效的特征量。数据降维可以减少数据中特征量的相关关系，用稍低维度的特征表征原始数据，最大程度地保留数据的主要信息，去除次要信息，从而降低数据分析的难度[11]，避免了在高维特征空间搜索特征的复杂度，同时保证了变量的独立性和信息的完整性。

经常用于数据降维的方法是主成分分析(Principal Component Analysis, PCA)[12]。PCA的主要目的是寻找数量更少的变量代替原变量来反映事物的主要特征，同时这些变量是原变量的线性组合。设已有个主成分，对应的权重向量为，那么第+1个主成分的权重向量定义为

限制条件为第+1个主成分与前个主成分正交。

(4)

基于上述定义，PCA的主要方法是通过对协方差矩阵进行特征分解，得出数据的特征向量和特征值，按特征值降序排序后可以得出数据从主要到次要的成分分量，并且只取排序靠前的一些特征向量作为主成分保留下来，从而达到数据降维的目的。

2.3 高维特征提取

本文使用的高维特征提取方法基于核独立分量分析 (Kernel Independent Component Analysis, KICA)[13]。核方法是一种利用核函数进行非线性映射的方法。通过这种方式，低维度的数据被映射到高维度空间。其意义在于低维度难以分解或者分类的数据，在映射到高维空间之后会易于分解或分类。独立分量分析应用于低维数据的分解，假设从图像采样得到的数据集为，代表权重，独立分量集合，独立分量分析可以在没有先验知识的情况下，估计独立分量和分离矩阵：

KICA首先将数据映射到再生核希尔伯特空间(Reproducing Kernel Hilbert Space, RKHS)中，从而使在高维特征空间中的线性分离，变为原来低维空间的非线性分离，从而获得高维度特征：

(6)

其中，代表输入数据，是在上的RKHS，是特征映射，为核函数。为了使特征空间搜索到的特征统计上独立，定义任意两个特征的相关性为

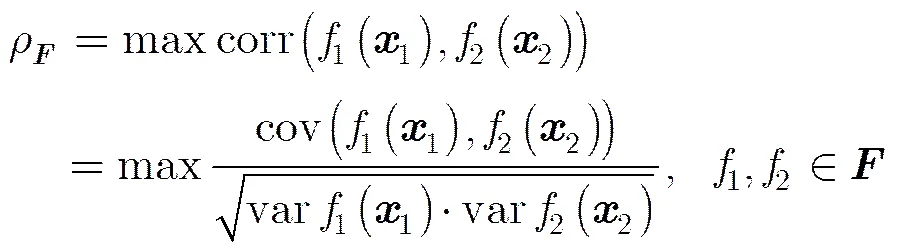
(8)

由于对比函数为非负，当且仅当变量独立的时候为0。通过以上步骤，这个特征空间中提取出来的特征能够作为本文中用来分析图像质量的特征。

3 基于高维度特征分析的图像质量评价方法

上一节介绍了本文数据处理和特征提取的核心方法。这一节将介绍结合这些方法的图像质量评价方法设计以及特征到质量的综合策略。考虑到高维特征空间的稀疏性和高维特征的复杂性，本文介绍的图像质量评价方法只考虑全参考方法的设计。

本方法首先将原始图像和失真图像转化为灰度图，在原始图片中进行数量较大的随机采样，取出窗大小为的采样的图像块数据。该采样基于以下假设：图像中的每个分块对于图像质量的贡献都是同等的，大量的采样能够从统计上满足大数定律，即大量重复的随机事件会呈现必然的规律，即随机变量对于图像质量的贡献会随着数量的增大而逐渐逼近结果。之所以采用这种大小的窗是因为太小的窗会导致过多的采样，样本的维度本身不高，所以用于独立分量分析的数据过分集中，会有可能产生不满秩的问题；太大的窗虽然使得样本维度变高，高维度的特征空间特别大，但是却没有足够的样本从特征空间中取得独立特征，一样不利于质量分析。

接下来利用块匹配，通过计算频谱的欧氏距离，去掉误差小于一定阈值的相似的图像块，完成空域上的数据筛选，并按照相同的位置对失真图像进行同样的图像块采样。通过将这些采样数据进行主成分分析，获得降维的数据。按照特征值大小排序后的主成分，能够将采样数据的维度从采样图像块数量乘以窗大小的维度降低到主成分个数乘以窗大小的维度。本实验中取用较少数量的主成分将代替原始采样数据用作图像质量评价分析。

最后利用核方法将数据映射到RKHS上进行独立分量分析，提取出高维特征，并利用综合策略将特征与质量产生映射关系。流程如图1所示。

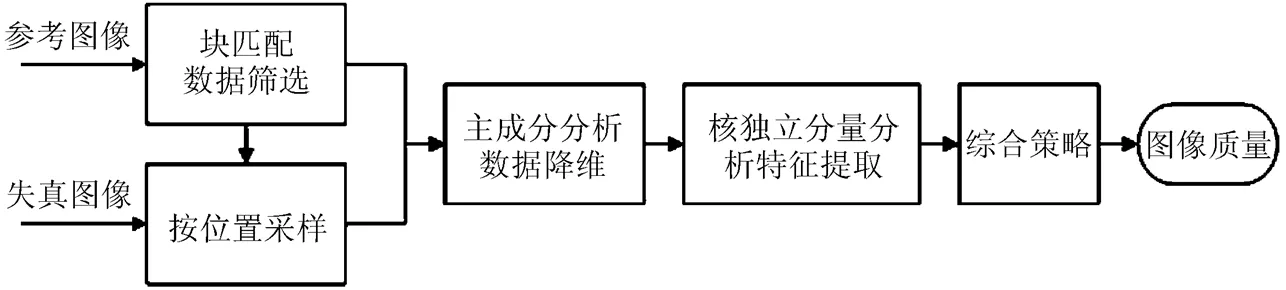
图1 本文算法流程框图

本文中采用的综合策略基于自然图像统计特性。自然图像统计特性基于引入的图像失真改变了图像特征的统计特性的假设，所以具有较为广泛的应用场景。考虑到高维特征的复杂性，利用自然图像统计特性分析特征间的差异并与质量产生映射是本文提出的客观图像质量评价方法的主客观一致性的根本原因。因此本文通过计算原始图像和失真图像的特征的相关系数的均值进行质量综合。从相关系数的性质上来说，两个变量的内容相似程度越高，统计特性上体现的相关系数越大；相反，如果引入的失真使得图像内容发生了很大的变化，那么与原始图像数据相比，统计特性上体现的相关系数越小。利用这个特点，我们可以将相关系数的差异与图像质量产生映射关系。综合策略为

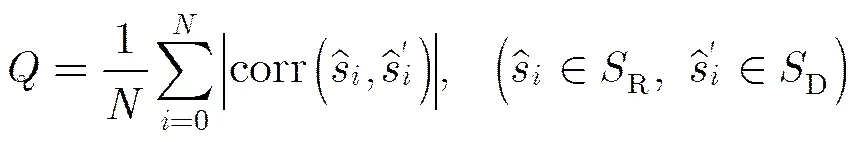
(10)

4 实验结果

本文设计的方法使用Matlab语言在LIVE (Laboratory for Image & Video Engineering)数据库[14]中完成测试。实验平台为CentOS下的Matlab Linux 2011a。数据库由美国德州大学奥斯丁分校开发并提出，其中包含了快衰落失真145幅，高斯模糊145幅，JPEG2000压缩失真175幅，JPEG压缩失真169幅和高斯白噪声失真145幅。数据库同时提供了每一种失真的参考图片和每一张失真图片的人的差分平均意见得分(DMOS)。为评价客观图像质量评价方法和人的主观评价之间的一致性，我们在得出每一幅失真图片的客观评价结果后，采用皮尔森线性相关系数(PLCC)和均方根误差(RMSE)来计算客观评分和主观评分的关系。PLCC值介于0和1之间，用来描述预测的准确性和单调性。RMSE值用来描述和主观分数的一致性。PLCC值越接近1，RMSE值越小，代表算法的性能越好。

本文选取了PSNR, SSIM和MSDD[15]进行对比分析。PSNR是误差模型中的典型代表，SSIM和MSDD是结构信息和分解变换模拟人眼视觉特性的方法中的典型代表。从数据库中所有图片得出的评价方法结果和DMOS值之间的PLCC数据为：PSNR为0.8723, SSIM为0.9449, MSDD为0.8900，而本文方法为0.9558。由此可以看出本文方法在LIVE数据库中得出的结果具有明显的优势。

表1和表2分别展示了本文方法与其它方法针对各种失真类型的PLCC和RMSE比较结果。图2为本文方法在LIVE数据库中各失真类型，所有图片的主观和客观的分数的散点图，纵坐标为数据库提供的人的主观评分DMOS，横坐标为本文方法得出的客观评价结果。对散点图的拟合曲线越趋近于线性，说明主客观评价结果越一致。

表1本文方法与PSNR, SSIM, MSDD针对各种失真类型的PLCC比较

表2本文方法与PSNR, SSIM, MSDD针对各种失真类型的RMSE比较

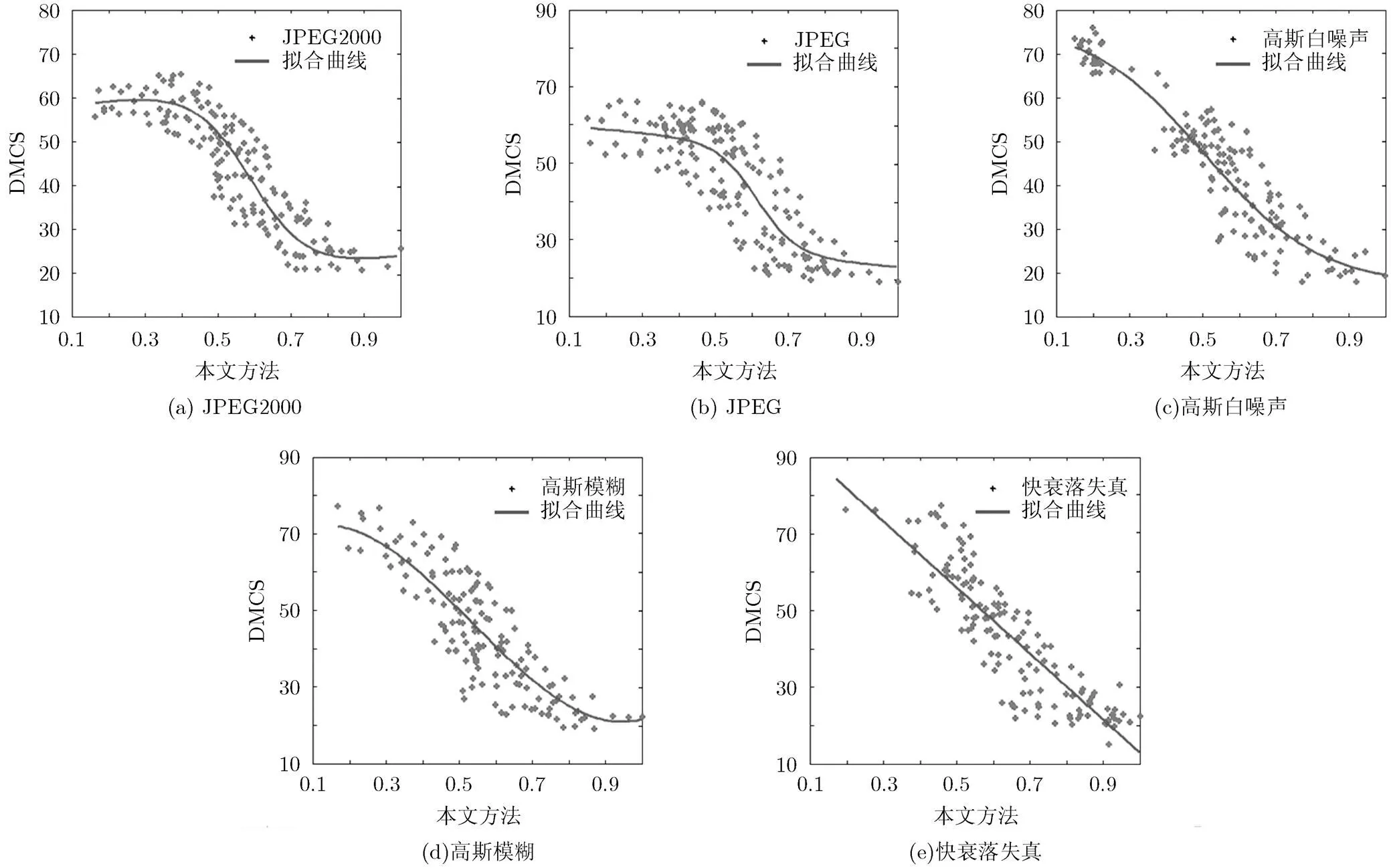
图2 LIVE数据库各失真类型本文方法与主观评价分数的散点图和拟合结果

(1)针对JPEG2000和JPEG压缩引入的振铃效应和块效应，本文方法有较好的评价结果和较好的稳定性。这是由于大范围采样和块匹配方法产生的非局部的数据较好地保留了块效应和振铃效应的特征。

(2)针对高斯白噪声，本文方法仅次于PSNR。由于全参考可以提供原始图像，所以高斯白噪声可以通过失真图像与原始图像相减获得，PSNR根据其物理意义可以获得最好的评价效果。线性可分的噪声在经过非线性变换后也可分，所以本文方法也可以取得较理想的效果。

(3)针对高斯模糊失真，PSNR得到的结果最不符合人眼特征。由于高斯模糊是对图像进行低通处理，MSDD由于模拟人眼的多尺度和多通道特性，可以取得相对较好的效果。本文方法可以取得仅次于MSDD的结果，说明高维度特征针对高斯模糊具有一定的效果。

(4)由于快衰落是由于信号多径传输而产生的叠加，所以失真图片增加的信息很难通过结构分析和分解进行判断。因此，对高维特征的处理比对低维特征更合适。本文方法针对快衰落失真取得了对比之中最好的效果。

从散点图上我们也可以看出，本文方法针对高斯白噪声，高斯模糊和快衰落失真的拟合结果接近于线性，说明方法对于这3种失真类型与人的主观评价较为一致。并且从总体上来看，本文方法对于一定极限阈值之外的数据处理存在着优势，即对质量极好和极差的预测结果较为准确。图3中展示了本文方法对整体图像质量的预测与人眼主观评分DMOS的拟合结果，说明本文方法对各种不同类型的失真产生的预测结果较为均匀，且与人的主观评价有一致性。

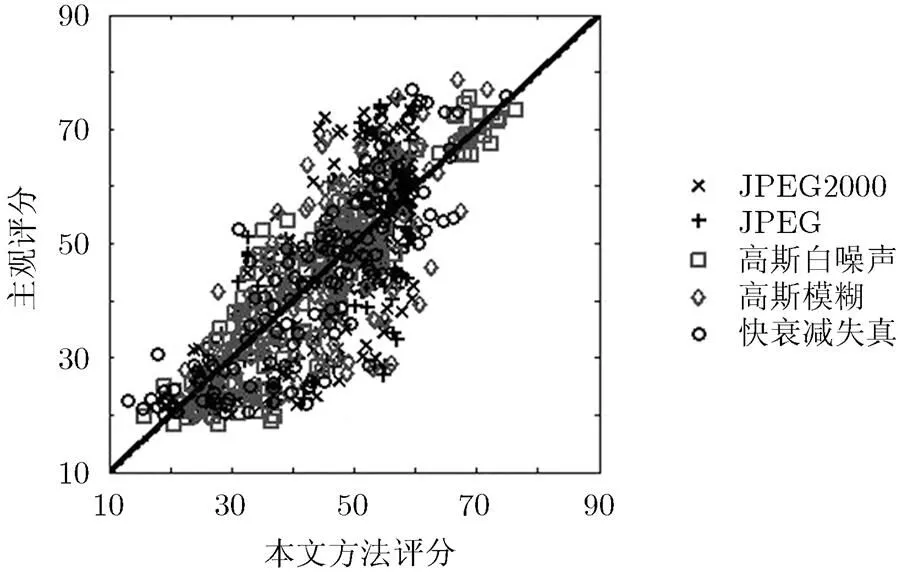
图3 LIVE数据库各失真实验结果散点图(横坐标为本文方法评分，纵坐标为主观评分)

5 结束语

本文介绍了一种基于高维度特征提取的图像质量评价方法。首先应用块匹配的方法筛选出了频谱不同的非局部的采样图像块，通过主成分分析进行数据降维。其次应用核方法将特征空间从低维度映射到高维度的RKHS特征空间上，利用高维空间上的独立分量分析提取的分量作为特征，最后经过综合策略，与质量产生映射，得到预测的图像质量。本文方法在综合阶段仍有改进的空间，并且可以在今后的研究中，挖掘原始图像高维度特征的共性，研究基于高维度特征的半参考及无参考图像质量评价方法。

[1] HE L, GAO F, HOU W,. Objective image quality assessment: A survey[J]., 2014, 91(11): 2374-2388. doi: 10.1080/ 00207160.2013.816415.

[2] WANG Zand BOVIK A C. Reduced-and no-reference image quality assessment[J].2011, 28(6): 29-40. doi: 10.1109/MSP.2011.942471.

[3] HU A, ZHANG R, YIN D,. Image quality assessment using a SVD-based structural projection[J].:, 2014, 29(3): 293-302. doi: 10.1016/ j.image.2014.01.007.

[4] HYVARINEN A, HURRI J, and HOYER P O. Natural Image Statistics: A Probabilistic Approach to Early Computational Vision[M]. US, Springer Science & Business Media, 2009, Chap 4. doi:10.1007/978-1-84882-491-1.

[5] HORE A and ZIOU D. Image quality metrics: PSNR vs. SSIM[C]. 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 2010: 2366-2369. doi: 10.1109/ICPR.2010.579.

[6] GAO X, LU W, LI X,. Wavelet-based contourlet in quality evaluation of digital images[J]., 2008, 72(1): 378-385. doi:10.1016/j.neucom.2007.12.031.

[7] DING Y, DAI H, and WANG S. Image quality assessment scheme with topographic independent components analysis for sparse feature extraction[J]., 2014, 50(7): 509-510. doi:10.1049/el.2013.4298.

[8] LUO C, WANG Y, DING Y,. Image quality assessment based on independent component analysis[C]. IEEE 2014 12th International Conference on. Signal Processing (ICSP), Hangzhou, China, 2014: 922-927. doi:10.1109/ICOSP.2014. 7015139.

[9] MANIKANDAN L C and SELVAKUMAR R K. A new survey on block matching algorithms in video coding[J]., 2014, 3(2): 121-125.

[10] ZHONG H, MA K, and ZHOU Y. Modified BM3D algorithm for image denoising using nonlocal centralization prior[J]., 2015, 106: 342-347. doi:10.1016/ j.sigpro.2014.08.014.

[11] SHLENS J. A tutorial on principal component analysis[J]., 2014, 58(3): 219-226.

[12] ABDI H and WILLIAMS L J. Principal component analysis[J].:, 2010, 2(4): 433-459. doi: 10.1002/wics.101.

[13] BACH F R and JORSAN M I. Kernel independent component analysis[J]., 2003, 3: 1-48.

[14] SHEIKH H. R, WANG Z, CORMACK L,. LIVE image quality assessment database release 2[OL]. http://live.ece. utexas.edu/research/quality, 2006.

[15] LIU M and YANG X. Image quality assessment using contourlet transform[J]., 2009, 48(10): 107201-10.

Image Quality Assessment Based on Non-local High Dimensional Feature Analysis

DING Yong LI Nan

(Institute of VLSI Design, Zhejiang University, Hangzhou 310027, China)

Traditionally, low dimensional features for partial information are extracted to analyze image quality. Though high dimensional features are difficult to be analyzed, they contain more information to fully analyze image quality. On this condition, this paper proposes an image quality assessment method based on non-local high dimensional feature analysis after optimized data sampling. Firstly, image data is filtered by using block matching method and dimensionally reduced by Principal Component Analysis (PCA). Secondly, Kernel Independent Component Analysis (KICA) is applied to extract high dimensional features. The features are finally synthesized to evaluate image quality based on natural image statistics. The experimental results show that the proposed method keeps accordance with human objective perception.

Image quality assessment; High dimensional feature; Non-local; Kernel Independent Component Analysis (KICA)

TN911.73

A

1009-5896(2016)09-2365-06

10.11999/JEIT151430

2015-12-08；

2016-04-18；

2016-06-12

国家863计划(2015AA016704c)，浙江省自然科学基金(LY14F020028)

The National 863 Program of China (2015AA016704c), Zhejiang Provincial Natural Science Foundation (LY14F020028)

李楠 linan@vlsi.zju.edu.cn

丁 勇： 男，1974年生，副教授，研究方向为多媒体处理及可重构计算、视频/图像质量客观评价、SoC设计与测试方法研究、医学图像处理与智能诊断.

李 楠： 男，1992年生，硕士生，研究方向为图像质量客观评价.