基于改进型快速双线性参数估计的复杂运动目标ISAR成像

吕 倩 苏 涛



基于改进型快速双线性参数估计的复杂运动目标ISAR成像

吕 倩*苏 涛

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对复杂运动目标的逆合成孔径雷达(ISAR)成像中多普勒扩散导致的成像质量下降，该文在建立方位回波信号为立方相位信号(CPS)的基础上，提出一种基于改进型快速双线性参数估计的复杂运动目标ISAR成像方法。该方法通过利用双线性立方相位函数，非均匀快速傅里叶变换(NUFFT)，基于Chirp-z的尺度变换以及快速傅里叶变换(FFT)等操作，能够快速实现CPS参数估计和复杂运动目标的ISAR成像。由于实现过程均采用NUFFT和FFT快速实现，该方法计算量小，并且双线性操作可以保证其具有较好的抗噪声性能和交叉项抑制性能。理论分析和仿真结果验证了该ISAR成像算法的有效性。

逆合成孔径雷达；立方相位信号；参数估计；非均匀快速傅里叶变换

1 引言

逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像因其在民用和军事应用中的重要作用，一直以来都是国内外研究的热点[2][3][4][5][6][7]。当目标匀速转动时，传统的方法直接采用傅里叶变换来实现基于距离-多普勒(RD)算法的ISAR成像。但对于复杂运动的目标，如海面上的舰船或空中高机动目标，方位回波的高阶相位项将导致多普勒扩散，降低ISAR方位成像质量，因此，传统的RD算法和LFM模型[9]已不再适用，必须将方位回波信号建模为立方相位信号(Cubic Phase Signal, CPS)的形式[4][5][6][7]。

相比于LFM信号模型，CPS模型在复杂运动目标的ISAR成像中具有更广泛的应用。CPS参数估计算法可细分为线性估计算法，双线性估计算法以及非线性估计算法。线性估计算法具有较好的抗噪声性能，但计算量太大，并不适合ISAR成像处理。非线性CPS参数估计算法主要有HAF- ICPF[7], PGCPF[10], PHMT[11], DechirpClean[12], KTCRD[3], CRQCRD[8], MLVD[13]以及文献[14]提出的基于SCFT参数估计算法。然而非线性变换会造成抗噪声性能和交叉项抑制性能的损失，从而影响该类算法在ISAR成像中的实用性。双线性参数估计算法，由于其较好的抗噪声性能和交叉抑制性能而备受关注。文献[15,16]提出的LPWD算法是通过搜索方式实现信号参数估计的，运算量大，不易实现[17]。文献[17]提出基于参数空间转换(Parameter Space Switching Method, PSSM)的快速双线性CPS参数估计算法，虽然改善了抗噪声性能，但参数空间转换操作使得该算法的计算量高达，并不易于实时处理。

针对以上问题，本文提出了基于改进型快速双线性参数估计的复杂运动目标ISAR成像方法。该方法在对雷达原始回波数据完成距离脉压和运动补偿后，首先利用NUFFT得到信号的慢时间-多普勒频率分布(Slow Time-Doppler Frequency Distribution, STDFD)，再沿多普勒轴求其逆傅里叶变换(Inverse Fast Fourier Transform, IFFT)，将其转换回慢时间-伪时间空间。最后，利用基于Chirp-z的尺度变换(Scale Transform, ST)和快速傅里叶变换(Fast Fourier Transform, FFT)快速实现信号去耦处理和能量积累，进而实现快速CPS参数估计和实时ISAR成像。最后，利用仿真数据对算法的有效性进行了验证和分析。

2 改进型快速双线性参数估计算法

本文采用文献[5,17]提出的复杂运动目标的ISAR成像模型。假设距离脉冲压缩和运动补偿已完成，这里只关注由目标转动所引起的多普勒扩散。第个距离单元的回波信号包含多个分量CPS，具有式(1)形式：

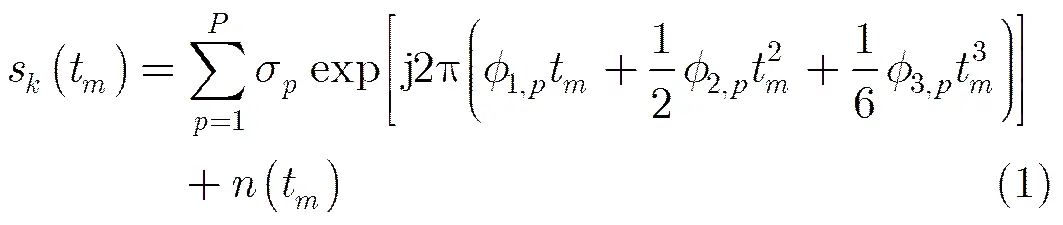
2.1单分量CPS的改进型快速双线性参数估计

考虑单个无噪声CPS，如

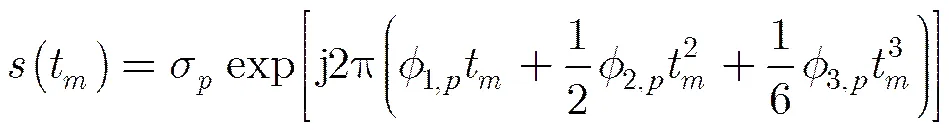
对式(2)求取双线性立方相位函数(Cubic Phase Bilinear Function, CPBF)，得到

(3)

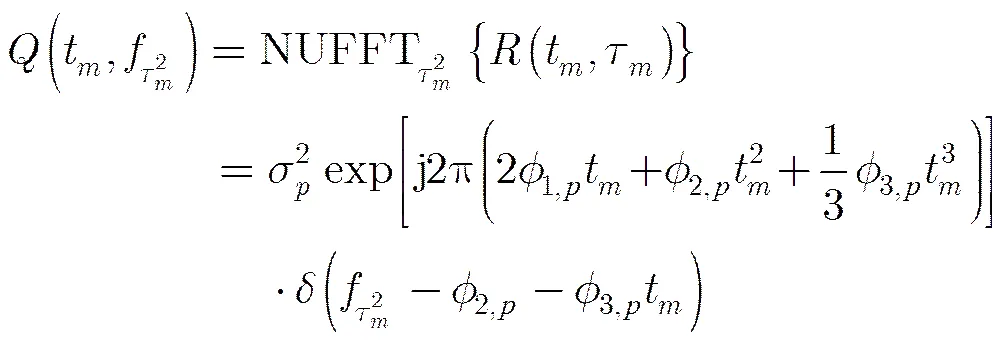
步骤1 对单个CPS求其双线性立方相位函数(CPBF)

(6)

(8)

(10)

因此，本文提出的改进型快速双线性CPS参数估计算法实现过程如式(11)：

可以看出，本文方法仅需要FFT, NUFFT以及基于Chirp-z的ST变换即可，由于基于Chirp-z的尺度变换可以使用FFT快速实现，降低了计算量。

2.2 多分量CPS的改进型快速双线性参数估计

如上所述，为获得目标的高分辨ISAR图像，各距离单元的回波信号必然同时存在多个CPS，如式(1)。因此，验证该算法适合不适合用于高分辨ISAR成像，必须对其处理多分量CPS的能力予以验证。下面以两分量CPS进行分析，其他多分量情况类似，这里不再详述。假设

则其CPBF为

(13)

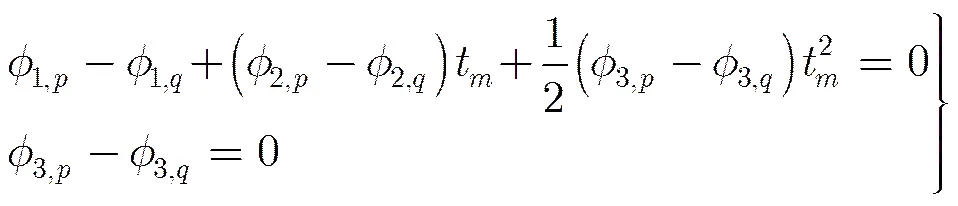
满足时，该影响才可以被消除。即只有当同时满足时，交叉项才会扰乱信号自身项的能量分布。而在实际ISAR成像应用中，并不会出现这种情况[17]，因此，交叉项的存在并不会影响自身项的检测。后面的章节中会用仿真实验来证明上述公式推导。

3 改进型快速双线性参数估计算法性能分析

3.1交叉项分析

图1 仿真实验结果

3.2 计算量分析

文献[14]所提的基于SCFT参数估计算法中，四阶瞬时自相关函数的计算量为，基于Chirp-z的尺度变换计算量为，关于非均匀采样轴的离散傅里叶变换的计算量为。因此，基于SCFT参数估计算法的计算量高达。

文献[17]所提的基于PSSM参数估计算法中，双线性立方相位函数的计算量为，利用NUFFT关于非均匀采样轴的离散傅里叶变换的计算量为，但是该算法中所使用的空间转换操作需要高达次循环累加操作。因此，基于PSSM参数估计算法的计算量也为。

本文所提的改进型快速双线性参数估计算法中，双线性立方相位函数的计算量为，利用NUFFT关于非均匀采样轴的离散傅里叶变换的计算量为。两次快速傅里叶变换和基于Chirp-z的尺度变换的计算量分别为和。因此基于本文所提的参数估计算法的计算量仅为。表1为3种CPS参数估计方法的计算量，相比于基于SCFT和基于PSSM的参数估计算法，本文所提的改进型快速双线性参数估计算法的运算量明显较低，有助于实时ISAR成像应用。

表1计算量分析

需要强调的是，文献[6]中利用NUFFT来加速实现基于SCFT的CPS参数估计算法，使得该算法的计算量级也达到了，但是其抗噪声性能只有。

3.3抗噪声性能分析

本节将利用输入输出SNR[8]以及MSE[20]来衡量改进型快速双线性CPS参数估计算法的抗噪声性能。考虑单分量CPS并加入高斯白噪声，其中CPS的参数设置为。输入，对每一个输入SNR做200次试验求平均。

图2(a)给出了3种算法的输入输出SNR比较，并且用匹配滤波的结果作为参考评价。由于基于SCFT参数估计算法使用了四阶非线性相关函数，导致抗噪声性能相对较差，门限仅为[6]。而基于PSSM参数估计算法与本文的快速双线性CPS参数估计算法，均使用了双线性变换，可以保证较好的抗噪声性能，其门限可以达到。CR和QCR可以同时被准确快速地估计，有效缓解了误差传播，因此，该算法更适合于低信噪比的情况下的CPS参数估计。

图2 抗噪声性能仿真结果

图2(b)和图2(c)为改进型快速双线性CPS参数CR和QCR估计的MSE，同时给出了相对应的CRB。可以看出，在时，CR和QCR估计的MSE接近其CRB，这同时也证明了图2(a)的结果。

同样需要强调的是，虽然基于PSSM参数估计算法与本文提出的改进型快速双线性CPS参数估计算法同样具有较好的抗噪声性能。但是，根据第3.2节中的计算量分析可以看出，基于PSSM参数估计算法的计算量明显高于本文提出的快速算法，后面的仿真实验也验证了本文的快速算法在计算效率上的突出优势。

4 基于改进型快速双线性参数估计的复杂运动目标ISAR成像算法

实际应用中，多分量CPS中幅度较弱的CPS会被交叉项淹没，需用Clean技术来对不同强度的CPS进行分离，依次估计出所有CPS的参数。本节提出了基于改进型快速双线性参数估计的ISAR成像算法，具体实现步骤为：

步骤1 对原始回波信号进行距离脉冲压缩和运动补偿，将所有的目标散射点都校正到其初始的距离单元，得到第个(,为距离单元总数)距离单元的数据

(16)

步骤3 利用本文所提的快速参数估计方法得到其CRQCRD，通过峰值检测手段完成CR和QCR的估计

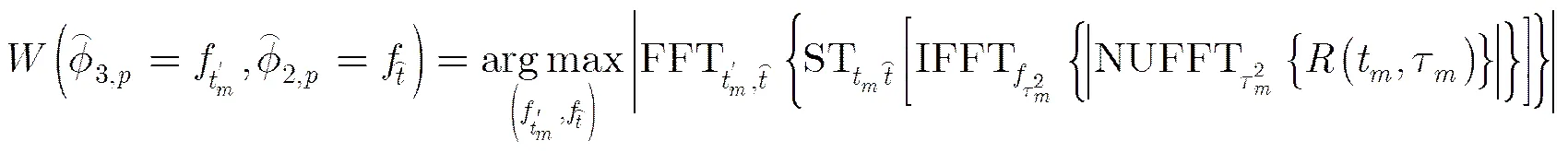
步骤4 利用已估参数补偿高阶相位项，消除多普勒扩散，进而完成幅度和CF的估计，有

(18)

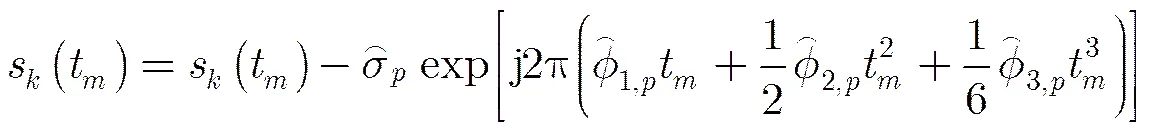
5 基于改进型快速双线性参数估计的ISAR成像仿真结果分析

5.1舰船目标的ISAR成像结果分析

本节将利用由理想散射点所构建的复杂运动的舰船(如图3(a))来验证基于改进型快速双线性参数估计的ISAR成像算法。雷达工作参数为：发射信号载频，信号带宽，采样频率，脉冲重复频率，回波个数为256。目标的转动参数为。

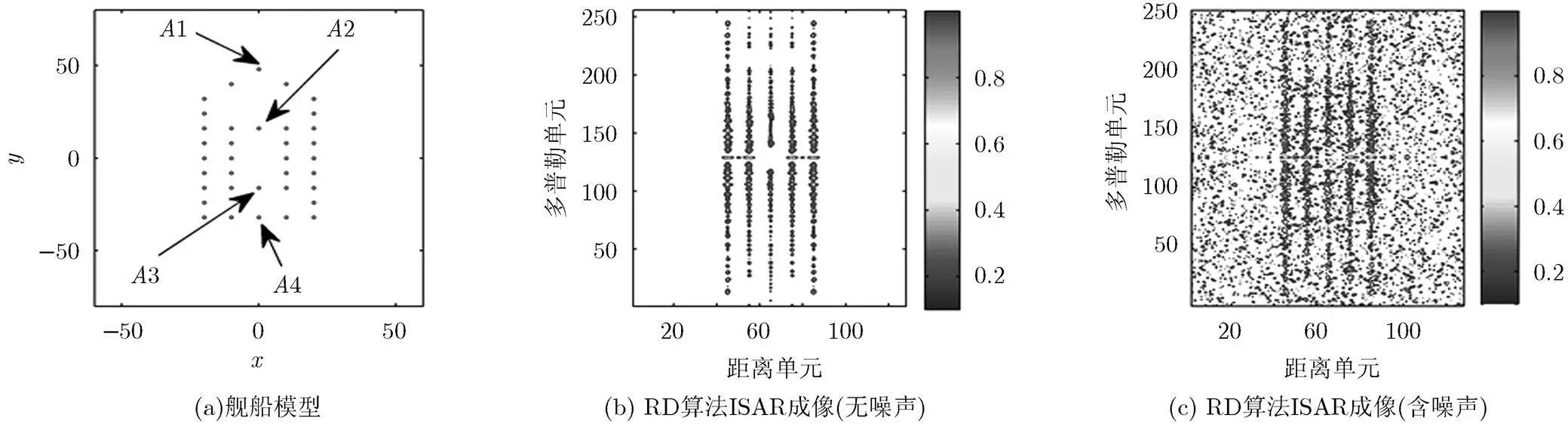
图3 舰船模型及基于RD算法ISAR成像结果

图4(a)为第65个距离单元的STDFD。可以看出，由于变量间的耦合，4个散射点的信号能量沿着不同的直线分布，并且存在大量的交叉项。利用本文所提的参数估计方法，可以快速得到该距离单元的CRQCRD，如图4(b)。4个散射点对应4个不同的尖峰，可以轻易地分辨开，并且通过峰值检测，可以得到4个散射点所对应的CR和QCR估计值。图4(c)中，4个散射点均可以被很好地重构，但是对于RD算法，由于存在多普勒扩散，信号能量分布不集中，无法聚焦各个散射点。

这里用熵作为衡量ISAR成像质量的标准[14]，图像的质量越好，其熵就越小[14][15][16]。与图5(a)相比，图5(b)和图5(c)中，几乎所有的散射点都被完好地重构，并且出现的伪散射点比较少。这是因为，基于SCFT参数估计算法利用四阶自相关函数，其交叉项较多，影响自身项的检测，而基于PSSM参数估计算法和本文所提的参数估计算法均为双线性变换，交叉项较少，有利于提高信噪比。表2中，图5(c)的熵要比其他的图的熵值要小，这说明图5(c)的成像质量更好。同样，根据表2可知，尽管基于PSSM的ISAR成像算法可以得到与本文所提算法相同的成像效果，但是其仿真时间明显高于本文所提的ISAR成像算法。因此，本文所提的基于改进型快速双线性参数估计的ISAR成像算法具有更广泛，更实际的应用。

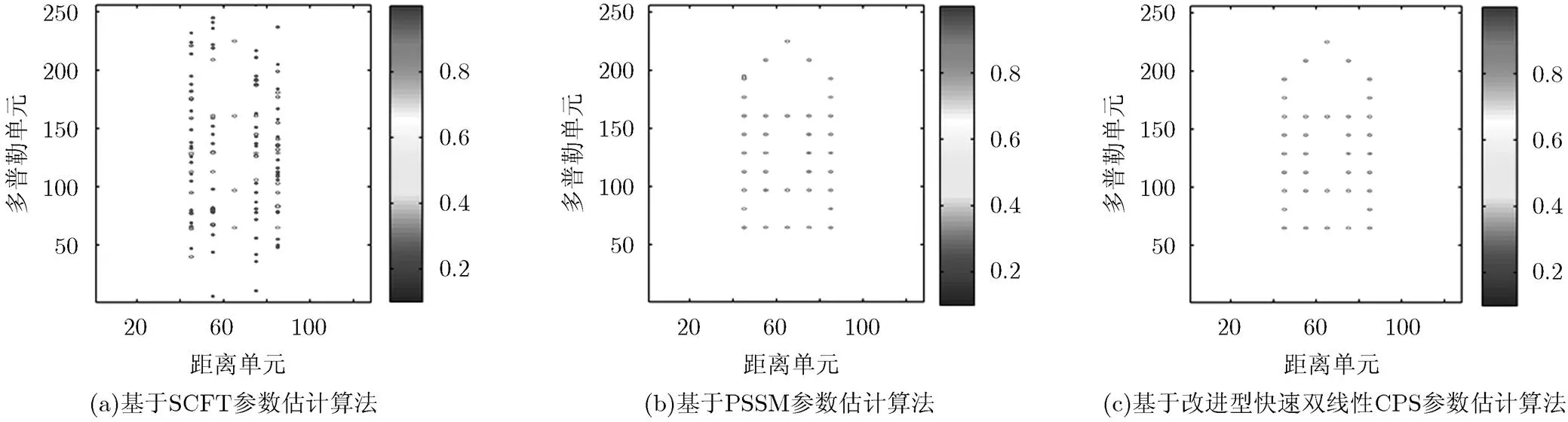
图5 舰船目标的ISAR成像

表2图5中的熵和仿真时间

5.2 飞机目标的ISAR成像结果分析

本节中，复杂运动的飞机目标是由141个理想散射点构建而成，如图6(a)，其转动速度，转动加速度，以及转动加加速度分别为。仿真中的雷达参数为：发射信号载频，信号带宽，采样频率，脉冲重复频率，回波个数为512。成像之前数据信噪比为，这里同样使用熵来评价图像的成像质量，表3给出了仿真结果的熵和所用时间。

图6 飞机模型及RD算法ISAR成像

表3图8中的熵和仿真时间

图6(b)为基于RD算法的ISAR成像结果，可以看出CR和QCR引起的多普勒扩散严重降低成像质量。另外，在信噪比为时，RD算法的ISAR成像结果已经完全淹没在噪声中，根本无法辨别，如图6(c)。这里提取第162个距离单元的数据进行分析，该距离单元中两个散射点和相邻较近。

图7(a)为相邻散射点和的WVD分布，可以得出，回波信号已不再适合LFM信号模型，而必须构建为CPS模型。图7(b)和图7(c)分别为两个相邻散射点的CRQCRD和补偿多普勒扩散后的结果，在图7(b)和图7(c)中，即使散射点相邻较近，依旧可以清晰地分辨出，并进行聚焦和重构。

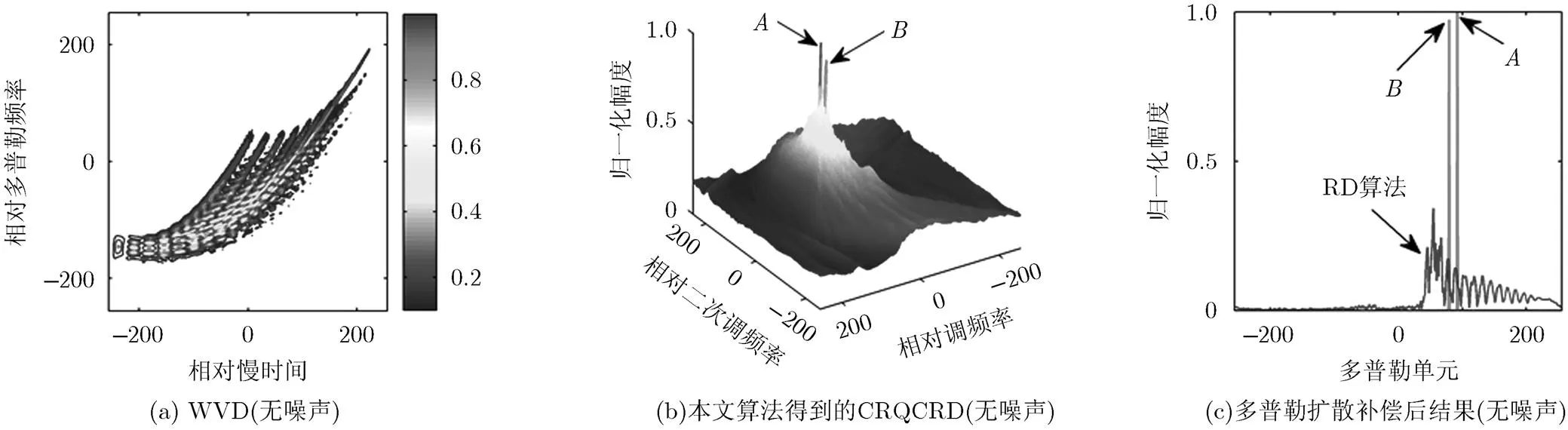
图7 相邻散射点仿真结果

图8中，相比基于SCFT的ISAR成像结果，其他两种算法均可以得到清晰的图像。从表3也可看出，图8(c)的熵最小，虽然图8(b)的熵接近于图8(c)，但仿真时间明显多于图8(c)。以上分析和结果都证明，本文提出的基于改进型快速双线性参数估计的ISAR成像方法，不仅具有较高的分辨率，较好的抗噪声性能和交叉抑制性能，而且计算量也相对较少，更加适合实际的ISAR应用。

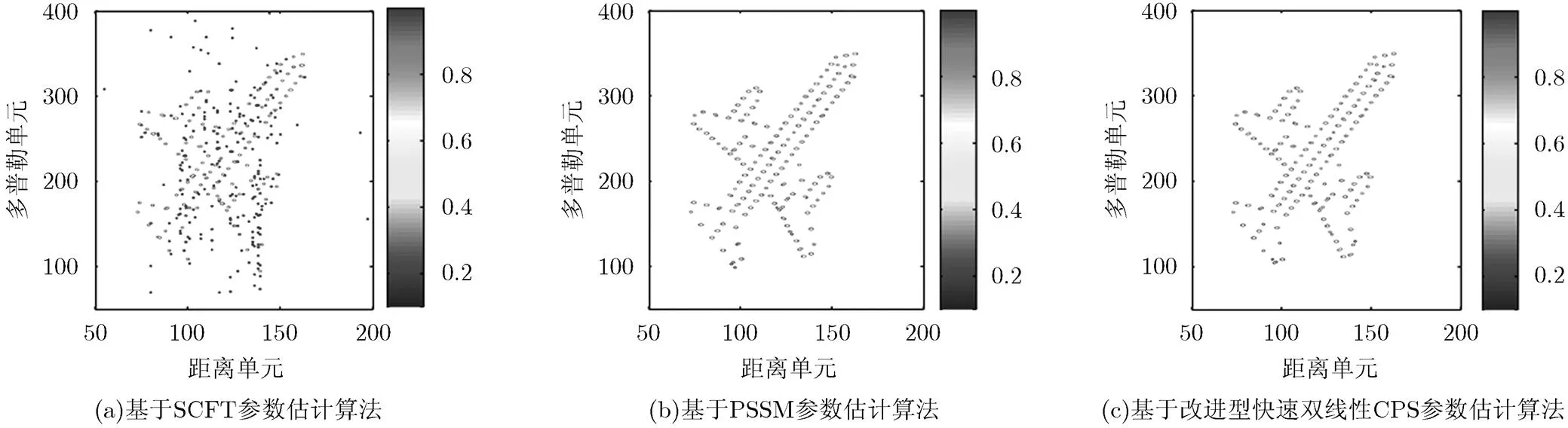
图8 飞机目标的ISAR成像

6 结束语

对空中或海面目标进行ISAR成像时，目标的复杂运动所产生的方位高阶相位项，会导致方位像的严重散焦，传统的RD算法和LFM模型不再适用。本文在CPS模型的基础上，提出了一种基于改进型快速双线性参数估计的复杂运动目标ISAR成像算法。该算法首先利用双线性立方相位函数、NUFFT以及IFFT运算，得到慢时间-伪时间函数，然后利用基于Chirp-z的尺度变换操作消除变量间的线性耦合，利用FFT进行能量积累，实现非搜索参数估计并重构ISAR图像。该算法通过有效利用NUFFT和FFT实现，可明显降低计算量，在抗噪声和交叉项抑制方面都有很大的改善，仿真结果证明了该方法的有效性和实用性。

[1] BERIZZI F, MESE E D, DIANI M,. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous Doppler technique: modeling and performance analysis[J]., 2001, 10(12): 1880-1890. doi: 10.1109/83.974573.

[2] XING Mengdao, WU R, LI Yachao,. New ISAR imaging algorithm based on modified Wigner-Ville distribution[J].,&, 2009, 3(1): 70-80.doi: 10. 1049/iet-rsn:20080003.

[3] ZHENG Jibin, SU Tao, ZHU Wentao,. ISAR imaging of targets with complex motions based on the keystone time-chirp rate distribution[J]., 2014, 11(7): 1275-1279. doi: 10.1109/LGRS. 2013.2291992.

[4] WU Liang, WEI Xizhang, YANG Degui,. ISAR imaging of targets with complex motion based on discrete chirp fourier transform for cubic chirps[J]., 2012, 50(10): 4201-4212. doi: 10.1109/TGRS.2012.2189220.

[5] WANG Yong and ZHAO Bin. Inverse synthetic aperture radar imaging of nonuniformly rotating target based on the parameters estimation of multicomponent quadratic frequency-modulated signals[J].,2015, 15(7): 4053-4061. doi: 10.1109/JSEN.2015.2409884.

[6] ZHENG Jibin, SU Tao, ZHU Wentao,. ISAR imaging of nonuniformly rotating target based on a fast parameter estimation algorithm of cubic phase signal[J]., 2015, 53(9): 4727-4740. doi: 10.1109/TGRS.2015.2408350.

[7] WANG Yong. Inverse synthetic aperture radar imaging of manoeuvring target based on range-instantaneous-Doppler and range-instantaneous-chirp-rate algorithms[J].,&2012, 6(9): 921-928. doi: 10.1049/iet- rsn.2012.0091.

[8] ZHENG Jibin, SU Tao, ZHANG Long,. ISAR imaging of targets with complex motion based on the chirp rate- quadratic chirp rate distribution[J].,2014, 52(11): 7276-7289. doi: 10.1109/TGRS.2014.2310474.

[9] LV Xiaolei, BI Guoan, WAN C,. Lv,s distribution: principle, implementation, properties, and performance[J].,2011, 59(8): 3576-3591. doi: 10.1109/TSP.2011.2155651.

[10] WANG Yong and JIANG Yicheng. Inverse synthetic aperture radar imaging of maneuvering target based on the product generalized cubic phase function[J]., 2011, 8(5): 958-962. doi: 10.1109/ LGRS.2011.2143387.

[11] WANG Yong and JIANG Yicheng. ISAR imaging of a ship target using product high-order matched-phase transform[J].,2009, 6(4): 658-661. doi: 10.1109/LGRS.2009.2013876.

[12] LI Yachao, WU R, XING Mengdao,. Inverse synthetic aperture radar imaging of ship target with complex motion[J].,&, 2008, 2(6): 395-403. doi: 10.1049/iet-rsn:20070101.

[13] LI Yanyan, SU Tao, ZHENG Jibin,. ISAR imaging of targets with complex motions based on modified Lv’s distribution for cubic phase signal[J]., 2015, 8(10): 4775-4784. doi: 10.1109/JSTARS.2015. 2460734.

[14] BAI Xia, TAO Ran, WANG Zhi-jiao,. ISAR imaging of a ship target based on parameter estimation of multicomponent quadratic frequency-modulated signals[J].,2014, 52(2): 1418-1429. doi: 10.1109/TGRS.2013.2251348.

[15] WANG Yong, KANG Jian, and JIANG Yicheng. ISAR imaging of maneuvering target based on the local polynomial wigner distribution and integrated high-order ambiguity function for cubic phase signal model[J]., 2014, 7(7): 2971-2991. doi: 10.1109/JSTARS.2014. 2301158.

[16] WANG Yong, ZHAO Bin, and KANG Jian. Asymptotic statistical performance of local polynomial wigner distribution for the parameters estimation of cubic-phase signal with application in ISAR imaging of ship target[J]., 2015, 8(3): 1087-1098. doi: 10.1109/JSTARS.2014.2355219.

[17] ZHENG Jibin, SU Tao, LIAO Guisheng,. ISAR imaging for fluctuating ships based on a fast bilinear parameter estimation algorithm[J]., 2015, 8(8): 3954-3966. doi: 10.1109/JSTARS.2015.2440911.

[18] 田超, 文树梁. 基于非均匀FFT的长时间相参积累算法[J]. 电子与信息学报, 2014, 36(6): 1374-1380. doi: 10.3724/SP.J. 1146.2013.01264.

TIAN Chao and WEN Shuliang. A long-term coherent integration algorithm based on non-uniform fast Fourier transform[J].&, 2014, 36(6): 1374-1380. doi: 10.3724/SP.J.1146. 2013.01264.

[19] LIU Qinghuo and NGUYEN N. An accurate algorithm for non uniform fast Fourier transforms (NUFFT,s)[J]., 1998, 8(1): 18-20. doi: 10.1109/75.650975.

[20] Peleg S and Porat B. The Cramer-Rao lower bound for signals with constant amplitude and polynomial phase[J], 1991, 39(3): 749-752. doi: 10.1109/78.80864.

ISAR Imaging of Targets with Complex Motion Based on the Modified Fast Bilinear Parameter Estimation

LÜ Qian SU Tao

(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

In view of image defocus caused by Doppler frequency shift in ISAR imaging of targets with complex motion, this paper characterizes the azimuth echoes as Cubic Phase Signal (CPS) and proposes an ISAR imaging algorithm for targets with complex motion based on the modified fast bilinear parameter estimation. This algorithm can achieve parameter estimation of CPS and ISAR imaging quickly by employing the cubic phase bilinear function, NonUniform Fast Fourier Transform (NUFFT), scale transform based on Chirp-z transform and Fast Fourier Transform (FFT). The computational cost is low due to the NUFFT and FFT in implementation procedure, and bilinearity guarantees a high anti-noise performance and a good suppression on cross-terms. The theoretical analysis and simulation results demonstrate the effectiveness of the proposed ISAR imaging algorithm.

Inverse SAR (ISAR); Cubic Phase Signal (CPS); Parameter estimation; NonUniform Fast Fourier Transform (NUFFT)

TN957.52

A

1009-5896(2016)09-2301-08

10.11999/JEIT151359

2015-12-03；

2016-05-04；

2016-07-14

国家自然科学基金(61271024, 61201283)，新世纪优秀人才支持计划(NCET-09-0630)

The National Natural Science Foundation of China (61271024, 61201283),Program for New Century Excellent Talents in University (NCET-09-0630)

吕倩 lvqian@stu.xidian.edu.cn

吕 倩： 女，1991年生，博士生，研究方向为雷达目标检测与参数估计、SAR/ISAR成像.

苏 涛： 男，1968年生，教授，研究方向为面向雷达、声呐、通信的高速实时信号处理、认知雷达.