面向复杂电磁环境的多天线信道估计技术
2016-10-13郭惠婷
胡 苏 郭惠婷 武 刚
面向复杂电磁环境的多天线信道估计技术
胡 苏*①②郭惠婷①武 刚①
①(电子科技大学通信抗干扰国家级重点实验室 成都 610054)②(信息感知技术协同创新中心 西安 710071)
对于基于认知无线电架构的多天线信道估计技术,由于传统零相关序列是在全部频谱可用前提下设计的,在复杂电磁环境的频谱限制下,传统零相关序列部分频域元素发生变化,且不再满足原始序列的周期相关特性,因此不能直接应用于复杂电磁环境的多天线信道估计。该文介绍了多天线通信系统的信道估计算法并指出对理想序列的要求,然后针对复杂电磁环境,即在存在频谱空穴的条件下,联合优化频谱受限和良好周期相关程度两大评价指标,设计出适用的序列集合,作为训练序列应用到认知无线电系统的信道估计算法中,仿真结果验证了新序列集合的有效性。
多天线信道估计;复杂电磁环境;频谱受限;序列设计
1 引言
复杂电磁环境泛指由密集、重叠、无序的电磁波构成的电磁环境,在军事领域特指作战时空内,人为电磁发射和多种电磁现象的总合。在信息化战场上,各作战要素效能的发挥直接依赖于相互之间的通信与协同能力,随着战场上智能化、信息化装备的逐渐增多,战场的电磁环境愈加恶劣,来自陆海空天不同作战平台上的电磁辐射在空间上互相交织、时间上持续不断、频域上密集重叠、效能上随机多变[1],如何应对复杂电磁环境,降低各种电磁干扰对通信的影响,已成为研究的重点方向。认知无线电技术能有效解决上述问题,通过感知周围电磁环境,找到空闲频段,实时调整系统工作参数以适应频谱变化,主动规避干扰,从而实现可靠通信[2]。由于用户与基站之间的相对运动和无线信号传播过程中的散射、衍射、反射[1],信道呈现出时变衰落特性,接收端通常需要获得信道状态信息才能进行相干解调,信道估计已成为无线通信的必要任务之一,也是决定认知无线电能否实现的关键技术之一。
对于面向复杂电磁环境的多天线移动通信系统,信道估计尤为重要,信道估计方案以及训练序列的相关性质对多天线系统的信道估计性能及复杂度起着决定性作用[3]。然而,对于复杂电磁环境下,传统零相关(Zero Correlation Zone, ZCZ)序列并不能直接应用,这是因为对于每个ZCZ序列,其设计是基于所有频谱可用的前提下的,在动态频谱约束条件下,频域对应的序列元素发生变化,因此传统序列集合将转变为新的序列集合,不再满足原始序列的相关特性[4]。其他具有良好相关性质的传统序列也是如此。
本文首先介绍了多天线通信系统的信道估计算法,然后针对复杂电磁环境,即存在频谱空穴的条件下,将复杂电磁环境中频谱资源受限和序列良好周期相关特性作为评价指标,利用最优化理论从源头上进行联合优化,设计出适用于频谱受限且周期互相关性能良好的序列集合,作为训练序列应用到认知无线电系统的信道估计算法中。仿真结果表明,相对于传统ZCZ序列,通过频谱资源受限和序列相关特性联合优化的序列集合能够有效地应用于认知无线电多天线系统的信道估计。
2 多天线系统的信道估计算法
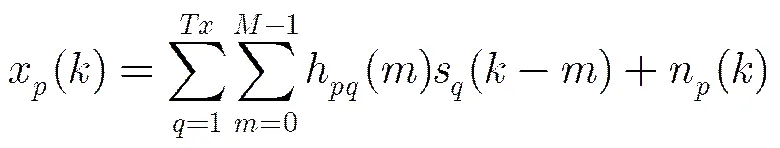
定义:
(2)
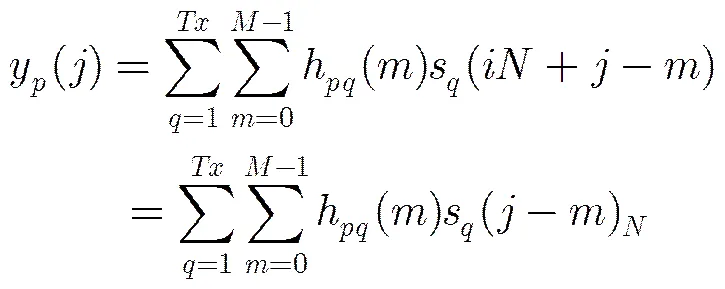
(4)
则式(4)可改写为
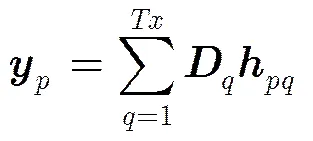
(6)
上述算法能够准确估计出所有信道的系数,但对采用的训练序列相关性能要求很高,通常采用ZCZ序列,当零相关区域时即可满足要求。但是在频谱受限的情况下,ZCZ序列不再满足正交特性,设频谱能效序列为(由0和1构成,空闲频点设为1,占用频谱设为0),原ZCZ序列为,则限制条件下的ZCZ序列可写成
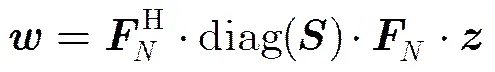
3 频谱限制下的良好周期相关序列集合设计
在许多实际场景中(如脉冲压缩雷达和无线通信环境),要求产生周期相关程度满足脉冲特性的序列,认知无线电系统则提出更高的要求,序列集合不但要具备良好周期相关程度,还要满足捷变要求,即能够随着复杂电磁环境的变化而变化,在频段被主用户(Primary User, PU)占用时设置为0,频段空闲时设置为1,可由次级用户(Second User, SU)使用以提高频谱利用率,如图1所示。文献[10,11]给出了频谱限制下具有良好非周期相关性能的序列设计算法,在此基础上加以改进,从而实现能够同时优化周期相关性能和满足频谱限制的理想序列。

图1 频谱限制示意图
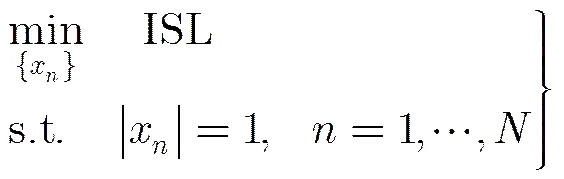
根据文献[11],首先给出ISL的频域表达式为
(9)

令
(11)
则ISL最小化问题可改写为
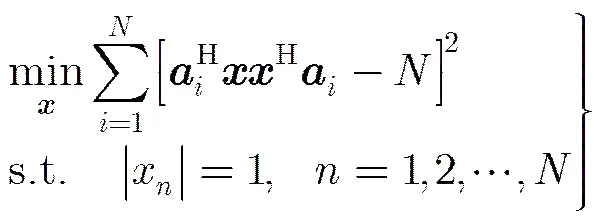
(13)
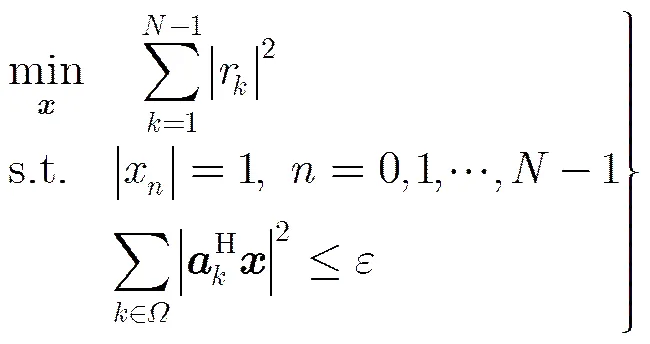
上述问题即为带有条件约束的最小化问题,采用最小优化算法并引入拉格朗日系数,可将问题转化为
(15)
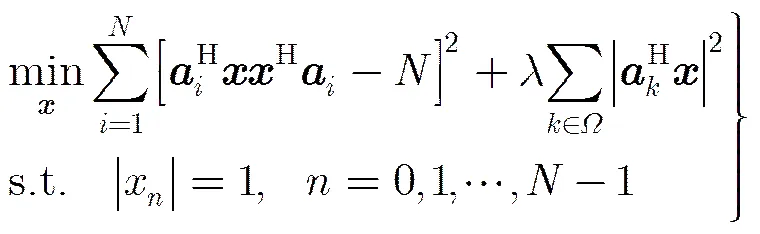
(17)

(19)
综上所述,要解决最小化问题,可采用迭代算法步骤如下:
(4)判断生成序列是否满足预设的迭代停止条件,为预定门限值如。若满足则算法结束,即为设计出的新序列;否则令,重复步骤(2)和步骤(3)。
上述算法能够生成一个联合优化周期相关函数和频谱限制的序列,但在多天线场景下,需要生成互相关性能良好的序列集合,因此对新序列进行扩展,构造相应的序列集合。基于该序列的理想周期自相关特性,可通过周期循环移位来构造相应周期序列集:设操作定义为对序列进行位右圆周移位操作,则满足条件的序列集合为,式中表示序列集合包含的序列数,对应于多天线通信系统的发射天线数,为周期移位位数,能够保证序列互相关函数在足够小,作为信道估计算法的训练序列必须满足(为信道抽头数目)。
4 仿真结果与分析
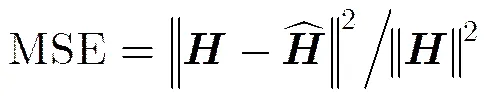
全部频谱可用时,ZCZ序列集合在零相关区内彼此正交,完全满足算法需求,图2为全部频谱可用时新序列集合的周期互相关程度,虽然新序列在对应区域内的互相关值达不到0,但互相关值足够小,可以忽略不计,因此在频谱不受限时能够取得很好的性能。在频谱空洞条件下,传统ZCZ序列无法满足正交特性,考虑单个PU的通信环境,即频谱能效序列,图3为新序列的频谱图,由图3可知新序列满足频谱空洞的约束。
图4(a)和图4(b)分别为该频谱限制条件下,ZCZ序列与新序列的周期互相关程度图。由上述给出的信道估计算法可知,该算法只要求序列集合在范围内的周期互相关函数足够小即可,由图4可得,新序列的相关程度明显优于频谱限制下的ZCZ序列。
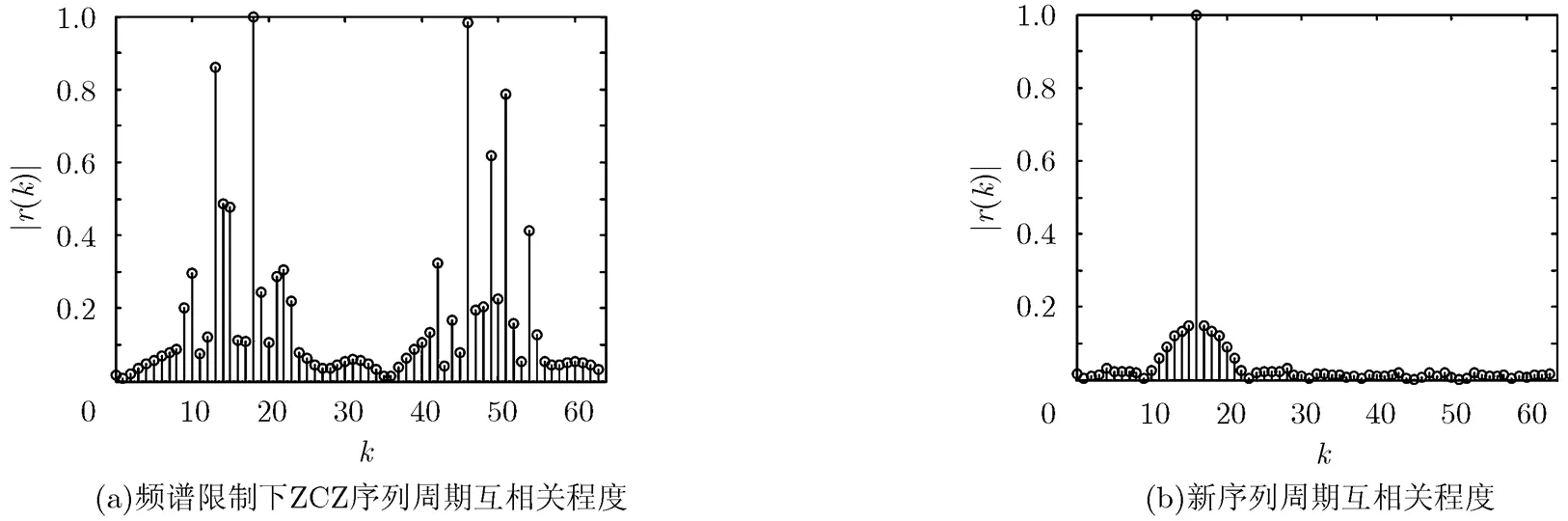
图4 频谱限制下ZCZ序列与新序列的周期互相关程度
变换域通信系统(Transform Domain Communication System, TDCS)作为频谱受限的典型通信系统[5,16],将上述设计的新序列和信道估计算法应用到MIMO-TDCS系统中,仿真参数同上,图5和图6分别对比了单个PU下,新序列和频谱受限ZCZ序列作为训练序列的MSE和BER性能。结合图4可知,基于频谱限制设计的新序列具有较好的周期互相关程度,因此信道估计性能优于传统ZCZ序列;理想信道指已知所有信道信息的情况,不需要做信道估计,因此其误码率性能最好;在处,新序列的性能相对ZCZ序列性能获取2 dB性能增益。
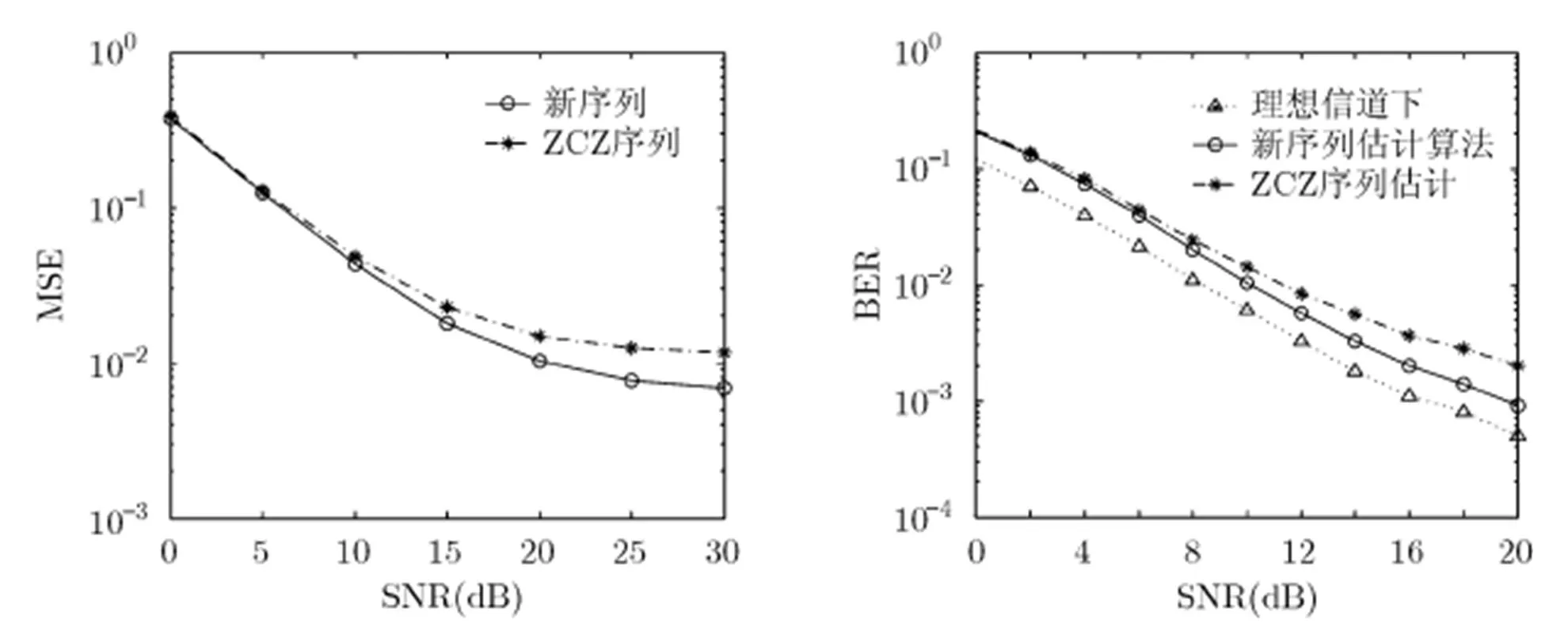
图5 单个PU时两种序列的信道估计MSE与SNR的关系 图6 单个PU时MIMO-TDCS系统BER与SNR的关系
在实际电磁环境下,频谱更加复杂多变,授权用户占用的频谱通常会随着时间、地理位置的变化而出现在任意频点位置,因此可用频点呈现出离散化趋势。在此考虑复杂电磁环境情况,即频谱出现多个挖孔,令,图7为约束下的新序列频谱图,新序列的频域特性与的分布一致。图8和图9分别为复杂电磁环境下的信道估计MSE和系统BER曲线。对比单个PU环境下,新序列能够保持较好的性能,而传统ZCZ序列的MSE和BER曲线大幅下降。
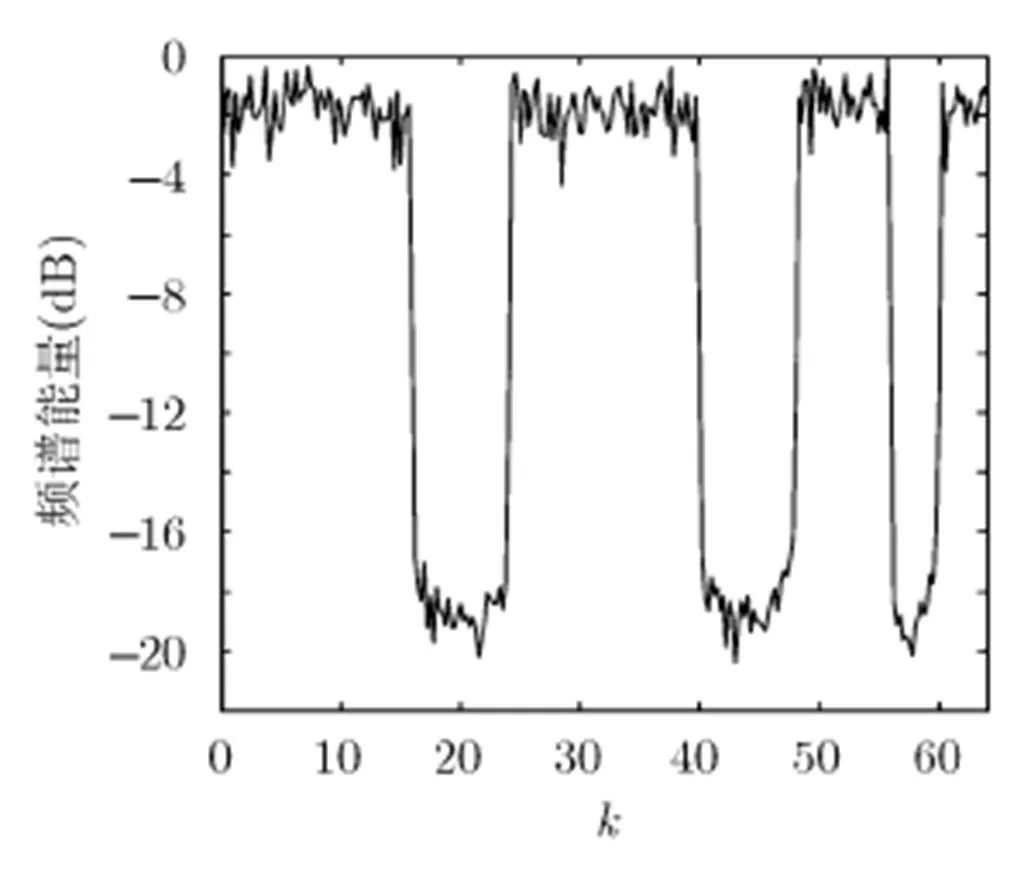
图7 复杂电磁环境下新序列图的频谱图

图8 复杂电磁环境下两种序列的信道估计MSE与SNR的关系 图9 复杂电磁环境下MIMO-TDCS系统BER与SNR的关系
分析仿真结果可以得到以下结论:(1)在全部频谱可用时,ZCZ序列存在零相关区且该区域内序列完全正交,新序列虽然不正交,但周期互相关值足够小,为-47 dB左右,其影响可忽略不计,因此两种序列的信道估计性能基本一致;(2)在频谱限制的情况下,ZCZ序列的相关性能大幅下降,新序列仍保持良好的周期相关性能;(3)新序列应用在信道估计上获得较好的MSE性能,提高了信号检测结果,降低了BER;(4)随着电磁环境的复杂化,可用频点逐渐离散分布,新序列作为训练序列实现信道估计时系统误码率能够满足实际需求,而传统ZCZ序列误码率性能随着电磁环境的复杂化而大幅度下降,由此验证新序列的有效性。
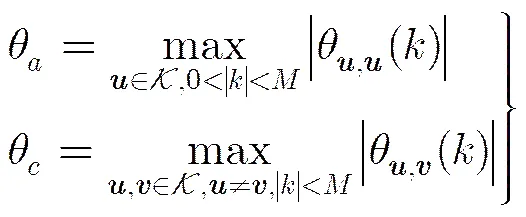
则序列集合各个参数需满足不等式:
(23)
5 结束语
随着周围电磁环境的复杂化,对于认知无线电架构下的多天线通信系统,传统ZCZ序列并不能直接应用,因此需要设计新序列以满足实际需求。本文首先介绍了多天线通信系统的信道估计算法,指出该算法是基于理想相关序列集合实现的,说明了在频谱受限条件下设计理想序列集合的必要性。然后针对频谱受限的多天线通信系统,联合优化频谱受限和良好周期相关程度两大指标,设计出适用于频谱受限且周期互相关性能良好的序列集合,作为训练序列应用到信道估计算法中。通过计算机仿真搭建MIMO-TDCS系统,验证了新序列性能优于传统ZCZ序列,获得较好的MSE性能,降低了系统误码率。
[1] MITOLA J. Cognitive radio-making software radios more personal[J]., 1999, 6(4): 13-18.
[2] 魏奇. 基于认知无线电抗干扰技术分析[J]. 无线电通信技术, 2011, 37(4): 56-58.
WEI Qi. Analysis based on cognitive radio anti-interference techniques[J]., 2011, 37(4): 56-58.
[3] 龚树平. 无线区域网与认知无线电中的信道估计技术研究[D]. [硕士论文], 电子科技大学, 2007.
GONG Shuping. Channel estimation technology research in the wireless area network and cognitive radio[D]. [Master dissertaion], University of Electronic Science and Technology of China, 2007.
[4] HU Su, LIU Zilong, and Guan Yongliang. Sequence design for cognitive CDMA communications under arbitrary spectrum hole constraint[J] ., 2014, 32(11): 1974-1986.
[5] 胡苏, 唐万斌, 王军. 变换域通信系统[M]. 北京: 国防工业出版社, 2015: 60-85.
HU Su, TANG Wanbin, and WANG Jun. Transform Domain Communication System[M]. Beijing: National Defence Industry Press, 2015: 60-85.
[6] AKIN S and GURSOY M C. Performance analysis of cognitive radio systems with imperfect channel sensing and estimation[J]., 2015, 63(5): 1554-1566.
[7] KIM Hyun Myung, KIM Dongsik, and KIM Tae Kyoung. Frequency domain channel estimation for MIMO SC-FDMA systems with CDM pilots[J]., 2014, 16(4): 447-457.
[8] OROZE LUGOA G, LARA M M, and MCLEMON D C. Channel estimation using implicit training[J]., 2004, 52(1): 240-254.
[9] ZHANG Peichang, CHEN Sheng, and HANZO L. Two-tier channel estimation aided near-capacity MIMO transceivers relying on norm-based joint transmit and receive antenna selection[J]., 2015, 14(1): 122-137.
[10] HE Hao, LI Jian, and PETRE S. Waveform Design For Active Sensing Systems[M]. UK, Cambridge University Press, 2012: 74-80.
[11] SONG Junxiao, PRABHU B, and DANIEL P. Optimization methods for designing sequences with low autocorrelation sidelobes[J]., 2015, 63(15): 3998-4009.
[12] SCUTARI G, FACCHINEI F, and SONG P. Decomposition by partial linearization: parallel optimization of multi-agent systems[J]., 2014, 62(3): 641-656.
[13] SOLTANALIAN M and STOICA P. Designing unimodular codes via quadratic optimization[J]., 2014, 62(5): 1221-1234.
[14] LUSS R and TEBOULLE M. Conditional gradient algorithms for rank-one matrix approximations with a sparsity constraint[J]., 2013, 55(1): 65-98.
[15] TSAI L S, CHUNG W H, and SHIU D S. Syntehsizing low autocorrelation and low PAPR OFDM sequences under spectral constraints through convex optimization and GS algorithm[J]., 2011, 59(5): 2234-2243.
[16] HU Su, GUOAN Bi, and GUAN Yongliang. TDCS-based cognitive radio networks with multiuser interference avoidance[J]., 2013, 61(12): 4828-4835.
[17] TSAI L S, CHUNG W H, and SHIU D S. Lower bounds on the correlation property for OFDM sequences with spectral-null constraints[J]., 2011, 10(8): 2652-2659.
[18] TANG X, FAN P, and MATSUFUJI S. Lower bounds on correlation of spreading sequence set with low or zero correlation zone[J]., 2000, 36(6): 551-552.
[19] WELCH L R. Lower bounds on the maximum cross correlation of signals[J]., 1974, 20(3): 397-399.
[20] SARWATE D V. Bounds on cross correlation and autocorrelation of sequences[J]., 1979, 25(6): 720-724.
Multiple Antenna Channel Estimation Technology in Complex Electromagnetic Environment
HU Su①②GUO Huiting①WU Gang①
①(National Communication Laboratory, University of Electronic Science and Technology of China, Chengdu 610054, China)②(Information Perception Technology Collaborative Innovation Center, Xi’an 710071, China)
For channel estimation technology of multiple antenna communication system based on cognitive radio architecture, traditional zero correlation zone sequences (which assume the availability of the entire spectral band) can not be used because their orthogonality will be destroyed by the spectrum hole constraint. This paper introduces the channel estimation algorithm in multiple antenna communication system and points out the requirement of the ideal sequence set, then on complex electromagnetic environment, i.e., under the condition of the existence of spectrum holes, joints optimization evaluation indexes of limited spectrum and good cycle correlation degree, designs a suitable sequence set, which can be applied to the channel estimation algorithm of cognitive radio system. The simulation results verify the effectiveness of the new sequence set.
Multiple antenna channel estimation; Complex electromagnetic environment; Limited spectrum; Sequence design
TN92
A
1009-5896(2016)09-2221-06
10.11999/JEIT151316
2015-11-25;
2016-04-18;
2016-06-16
国家863计划(2015AA8098083C),国家自然科学基金(61471100, 61101090),中央高校基金(ZYGX2015J012)
The National 863 Program of China (2015AA8098083C), The National Natural Science Foundation of China (61471100, 61101090), The Fundamental Research Funds for the Central Universities (ZYGX2015J012)
胡苏 husu@uestc.edu.cn
胡 苏: 男,1983年生,副教授,研究方向为多载波通信、认知无线电、LTE.
郭惠婷: 女,1991年生,硕士生,研究方向为信道估计、序列设计.
武 刚: 男,1975年生,教授,研究方向多天线技术、绿色通信.
