基于最大满意度的众筹筑屋规划方案设计
2016-10-13刘玉堂
刘玉堂,陈 静
基于最大满意度的众筹筑屋规划方案设计
刘玉堂,陈 静
(河南机电高等专科学校,河南 新乡 453003)
文章首先对2015年全国大学生数学竞赛D题的众筹筑屋设计方案进行分析、核算,然后建立以参筹者的最大满意度为目标的优化模型,给出了基于最大满意度的新设计方案,并核算了相关经济指标。
众筹筑屋;满意度;数学模型
0 引言
众筹,即大众筹资或群众筹资,是指一种向群众募资,以支持发起的个人或组织的行为。它具有低门槛、多样性、依靠大众力量、注重创意的特征,在互联网金融快速发展的浪潮下,众筹模式得到了越来越多人的认可,众筹筑屋就是互联网时代一种新型的房地产形式。2015年全国大学生数学竞赛D题[1]研究的就是这个问题。现有一个占地面积为102 077.6众筹筑屋项目,项目规定参筹者每户只能认购一套住房。在建房规划设计中,需考虑诸多因素,根据国家相关政策,不同房型的容积率、开发成本、开发费用等在核算上要求均不同,为了让项目参筹者对该项目进行了解和民主决策,本文首先将这个众筹筑屋项目原方案(方案Ⅰ)的成本与收益、容积率和增值税等信息进行公布,建立数学模型对该方案进行全面核算,给出相关的结果[2];接着通过对参筹者进行抽样调查,确定了参筹者对11种房型的购买意愿比例。在尽量满足参筹者购买意愿的前提下,建立了以参筹者的最大满意度为目标的优化模型,重新设计建设方案(方案Ⅱ),并对新方案的相关经济指标进行核算。
1 方案Ⅰ各项信息核算模型
下面利用参考文献[1]中给出的相关数据,对方案Ⅰ各项信息进行核算,主要包括容积率、成本、增值税、收益等经济指标。
1.1 容积率计算
1.2 项目成本计算
项目成本主要有四部分组成:取得土地使用权所支付的金额、房地产开发成本、房地产开发费用、与转让房地产有关的税金,下面我们对每个子项目分别计算这四项成本,然后计算出项目总成本。
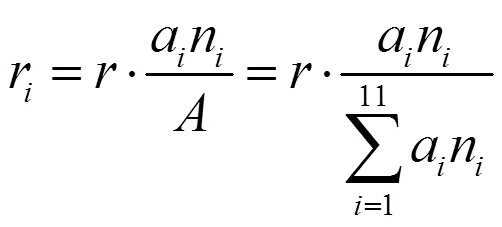

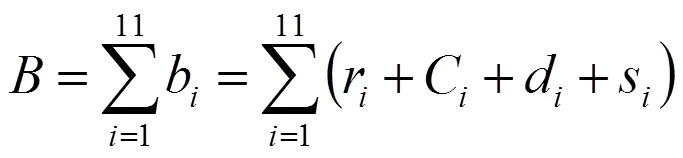
1.3 土地增值税计算
由参考文献[1]可知,我国的土地增值税采用四级超率累进税率,在计算土地增值税时需要计算增值额,以及扣除项目金额,并乘上相应的税率得出,下面我们分别计算每个子项目的扣除项目金额、增值额和增值税,然后再求出方案Ⅰ的增值税。


1.4 方案Ⅰ各房型各项经济信息统计

表1 方案Ⅰ各项经济信息统计表
由题意知,投资回报率达到25%以上的众筹项目才会被成功执行,投资回报率的计算[3]为利润/投资总额×100%,此处利润应为方案Ⅰ中总收益。由于土地增值税由建设房屋者支付,因此投资总额应包括总建设成本与土地增值税。所以,投资回报率的数学模型为,带入表1相关数据可得方案Ⅰ的投资回报率为14.79%,故而方案Ⅰ不能被很好的执行。下面我们来建立参筹者最大满意度优化模型。
2 最大满意度优化模型
2.1 模型建立
首先计算参筹民众对11种房型的满意比例,用MATLAB7软件对参考文献[1]中满意比例进行归一化处理,得到参筹民众对第个子项目的满意度,具体结果如表2所示。

表2 满意比例归一化结果
我们把各房型的建房套数与满意度之积的和看作目标函数,要使参筹者尽可能对新方案满意,即目标函数为求满意度最大值。设为方案Ⅱ中第种房型的建房套数,则目标函数为:,由题意知模型的约束条件有两类:一类是各种房型建设的最低套数约束和最高套数约束,另一类是国家规定住宅的最大容积率约束,容积率可用1.1中的容积率计算模型进行计算,即,综上所述,最大满意度优化模型为:

关于约束条件的说明:(1)在方案Ⅱ中每种房型预计建设套数必须满足城建部门规定的最低和最高限制;(2)容积率要满足国家要求;(3)预计建房为整数。其中,表示城建部门规定的第种房型的最低套数约束,表示城建部门规定的第种房型的最高套数约束。将模型输入Lingo10,即可求出各房型所需建房套数方案Ⅱ各房型建套数如表3所示。

表3 方案Ⅱ各房型建房套数
2.2 方案Ⅱ各项信息统计
根据方案Ⅱ所求各房型的建房套数,在房型面积、开发成本、售价等条件不变的情况下,采用方案Ⅰ的方法核算出方案Ⅱ的各项经济信息统计如表4。

表4 方案Ⅱ各项经济信息统计表
2.3 判断方案Ⅱ能否被成功执行
利用方案Ⅰ中投资回报率的计算方法,再带入表4相关数据,可得方案Ⅱ中投资回报率为,满足众筹项目的执行标准,因此我们认为方案Ⅱ能被成功执行,说明就投资回报率而言,方案Ⅱ明显优于方案Ⅰ。进一步将方案Ⅰ与方案Ⅱ的各项经济指标放在一起进行比较,具体比较结果如表5所示。

表5 方案Ⅰ与方案Ⅱ中各项经济信息比较表
观察上面表格发现,(1)对于方案Ⅱ而言,在用地面积不变的情况下,总房间套数比方案Ⅰ多了783套,因为该众筹项目有上万人参与,显然房间套数越多越能满足参筹者对房屋的购买意愿,也就是说方案Ⅱ更能满足人们的购房意愿;(2)就成本与收益来看,方案Ⅱ与方案Ⅰ相比较不仅成本低了118 215 023.5元,而且总收益提高了;(3)就投资回报率而言,方案Ⅱ的投资回报率大于方案Ⅰ;(4)两个方案的容积率相差无几,没有超出规定范围,符合建设要求。
综合以上分析,方案Ⅱ不仅符合房地产开发商的利益,而且更能满足参筹者对房屋的购买意愿,同时其投资回报率大于25%,所以,我们认为众筹筑屋方案Ⅱ能被成功执行。
(责任编辑吕春红)
[1] 全国大学生数学建模竞赛组委会.历年真题,2015年专科组D题[EB/OL].http://www.mcm.edu.cn/html_cn /node/ac8b96613522ef62c019d1cd45a125e3.html,2016-01-11.
[2] 姜启源.数学模型[M].北京:高等教育出版社,2011.
[3] 顿新春,代园伟,王博.基于WBS的房地产开发项目成本预算与成本控制研究[J].河北工程大学学报(自然科学版),2013,30(3):109-112.
New Planning of Building House by Crowdfunding Based on The Maximum Satisfaction
LIU Yu-tang,et al
(Henan Mechanical and Electrical Engineering College, Xinxiang 453003, China)
Firstly, this paper analyzed and calculated the planning of building house by crowdfunding of problem D in CUMCM 2015.Secondly, we established the objective optimization model for the highest target of satisfying people’s needs, then the new design scheme based on the maximum satisfaction is given, and the relevant economic indicators are calculated.
crowdfunding;satisfaction;mathematical modeling
O351.3
A
1008–2093(2016)02–0013–05
2016-02-03
刘玉堂(1981―),男,湖北襄阳人,讲师,硕士,主要从事应用数学研究。
