基于蒙特卡罗的消费投资决策模型研究

刘欢



基于蒙特卡罗的消费投资决策模型研究

刘欢

(湖南外贸职业学院工商管理学院, 湖南长沙, 410200)

将消费和投资放在一个跨期最优化框架下, 提出了基于蒙特卡罗风险评估的消费投资决策模型。首先, 建立个体效用函数、劳动收入、跨期预算约束、投资机会及市场摩擦因素之间的数学表达式。然后, 考虑劳动收入风险、投资收益风险, 建立消费投资组合动态优化模型。最后, 通过一个实例阐明所提出模型能更加有效地刻画实际市场中的消费投资情况, 证明所设计算法的有效性。

消费投资决策; 摩擦因素; 蒙特卡罗; 风险评估

消费投资选择系投资者在金融领域选择特定的资产开展投资, 从而提升投资者的实际资产数额, 同时利用对于此类财富的消费行为来提升自身的资产总额。基于离散时间的投资消费决策分别是Samuelso (1969)与Fama (1970)最早进行研究的。Merton[1]针对连续时间下的投资决策问题进行了研究。Karatzas等[2]在研究最优消费投资模型时考虑了投资人分散投资于有限个拥有风险资产的小投资人的情况; Cox和Huang[3]在研究最优消费投资组合决策时考虑了风险资产的价格遵循扩散过程的情形; Shreve等[4]将2个具有交易费用的债券投资组合作为实例进行最优化研究; Cuoco等[5]探讨了当投资者投资额度大时, 在最优消费投资时的投资组合方式和最优策略选择; Campbell等[6]研究了当考虑期望回报随时间变化的风险资产时如何进行最优化投资决策, 并给出了解决结果; Chacko等[7]考虑了风险资产收益率的数学期望及方差随时间变化情况下的最优消费投资规划问题。

20世纪90年代初, 我国在数学金融学方面的研究开始起步, 至今已取得了不错的研究成果。Wan[8]考虑遵循复合跳跃过程的股票价格, 建立了投资决策模型; 费为银[9]在研究中考虑了红利支付这一结算方式对原有的最优消费投资模型的影响, 并加以扩充; 丁传明等[10]在研究的消费投资模型中加入了对随机收入以及红利支付2个影响因素的度量; 费为银等[11]在研究中考虑了允许借贷的情形; 刘海龙等[12]对Merton研究的连续时间下的投资决策问题进行了分析并在非完全市场情况下进行推广, 提出了服从几何布朗运动的投资消费模型; 杨昭军等[13]研究了基于不完全信息下的投资消费决策方法并计算得到模型的显式解; 郭文旌[14]在股票服从几何布朗运动的基础上研究推广了当其服从跳跃-扩散过程时的投资模型; 肖建武[15]的研究是通过Legendre变换以及最优控制理论结合到常方差弹性模型的方法求得了模型的解析解。

近几年来, 消费投资决策问题基本理论日趋成熟, 然而, 由于理论的复杂性, 建立的理论模型与方法难以运用到实际中。为了研究出存在更多显式解的消费投资决策优化模型, 本文以消费投资决策为研究对象, 考虑市场摩擦因子、交易成本与消费支出、劳动收入、投资收益3类不确定性因素等对消费和投资选择行为的影响, 建立投资决策模型和蒙特卡罗风险评估模型, 研究并实现了新模型的求解方法。

1 消费投资决策优化模型

1.1 不确定性分解

1.1.1 投资收益不确定性

考虑在摩擦资本市场中有种风险资产Z(其收益率为)和一种无风险资产(其收益率为常数)。= (1,2, …,w+1)是一个投资组合,表示投资在第种资产的比例, 记为,表示资产投资者在开始时所拥有的资产的比例。此时, 投资组合除去税收红利交易费用后的投资收益为。

针对各种不存在风险的资产, 因为存款在实际存入的时候无需缴费, 仅在取出的时候需要交纳少数对利息所征收的税款。所以, 若属于取出存款时的具体交易费用系数, 则。

1.1.2 劳动收入的不确定性

国内的研究者通常利用人均可支配收入来充当劳动收入, 但因为该指标存在着一定的投资收益, 所以, 通过该变量来替代劳动收入显然是不妥的。因此, 本文在计算假设模型之中有关个体的实际收入包括收入和收益2部分。

劳动收入存在的不确定性, 即劳动收入在时的条件方差用来表示, 这一指标数值越大, 就表示民众收入增长率波动越大, 对于收入存在的不确定性日益增强。

1.1.3 消费支出不确定性

通过人均年消费增长率相对于平均值存在偏离率的平方数据, 来充当反应实际不确定性的配套指标, 同时实际工时为。该指标数值越高, 实际的消费增长率波动就越显著, 对于支出方面的不确定性就越明显。

根据收入分组数据中多个组别实际年支出增长率之间的方差, 来表述实际存在的不确定性, 具体的公式为, 其中,代表各个组别的实际权重。

1.2 最优投资组合动态模型

假设个体有着长久的生命, 而且也存在着一定的无工作几率。在无工作的情况下, 其实际的劳动收入维持在0; 在保持一份工作的情形下, 其收入符合前文的假设, 实际的行为决策目的在于使得预计中的幂消费效用实现最大化[16]。而其中个体跨期最优问题能够被表述为。服从预算约束,。

采用动态规划[9]的方法求解, 设价值函数为, 组建贝尔曼方程。换言之,时刻的具体价值函数, 和时刻的具体消费效用基本等同, 外加时刻贴现函数的期望值, 能够对公式的右侧项进行更为深入的优化操作, 同时契合各方面的预算限制, 得到,。在和间顺着最优化的路径有着简易包络关联[10], 而按照包括定理, 同时利用约束条件能够获得。从而得到欧拉方程。根据的实际状况, 具体的跨期最优化问题, 有概率存在着2大欧拉方程[11], 而保持有工作状态的情况下, 具体资产有。而在无工作状态下为, 其中变量表示决定变量价值的劳动收入状态。

1.3 最优消费动态模型

最优消费增长率模型阐述了影响个体预期的3个方面的要素。(1) 个体自身的主观贴现率。富有耐心而且主观贴现率较高的个体, 自发的愿意进行延迟消费。(2) 偏高的利率使得个体存在延迟消费的激励效应。而消费的延迟代表未来消费的增长, 进一步是整体消费走势偏向上。但是消费自身所存在的边际效应, 使得个体容忍已经偏离原本水平路径的期望。对比消费延迟激励所存在的变化, 个体存在的倾斜意愿称作是消费自身的跨期替代弹性, 在常相对回避系数的消费函数假定模型[12]里面, 消费自身所存在的跨期替代弹性这一项数据和另外一项的相对风险回避系数数据的倒数基本保持一致。在此情况下, 当相对更高的时候, 个体倾斜整体消费路径的意愿相对更低, 预期中的消费增长率对比无风险利率来说, 只存在微小的变动。(3) 消费不确定性效应。具备一定幂效用函数的各种对于风险较为厌烦的投资者, 针对实际存在的不确定性问题, 通常选择提升预防性储蓄的数额, 即提升,同时其消费路径也有着一定的向上倾斜。

2 禁忌模拟混合优化算法

将蒙特卡罗模拟[17]与禁忌搜索[18]结合设计混合算法, 从而处理消费投资决策分析里面的各种优化问题。对于这一类别的模拟则通过拉丁超立方分层抽样的方法来构成对应的初始解, 使得群体里面的个体存在于整体的解空间区域之中, 确保邻域范畴之内实际搜索空间的多样化演变, 开展的搜索并不会因此而遗漏各种局部最优解。与此同时在群体之中的各种个体, 利用禁忌搜索的方式来完成检索任务, 进一步提升群体的质量。在搜索流程之中调取有关的评价函数[15]来进行移动值的判定, 同时按照实际的移动值以及禁忌表来决定实际移动的接受状况。

3 实例验证

关于风险项目的具体选择, 更加契合0-1的Knapsack问题, 但是其中多个风险实际的回报难以界定, 假设回报依从于项目, 同时根据固定的概率来进行分布的一种随机变量, 在表格之中构建配套的随机模型, 利用禁忌搜索的形式, 来对于契合约束要件的各种值, 开展整体回报预测的模拟工作, 与此同时还需要计算具体的均值以及方差数据, 再度反馈于搜索流程之中, 从而实现优化。

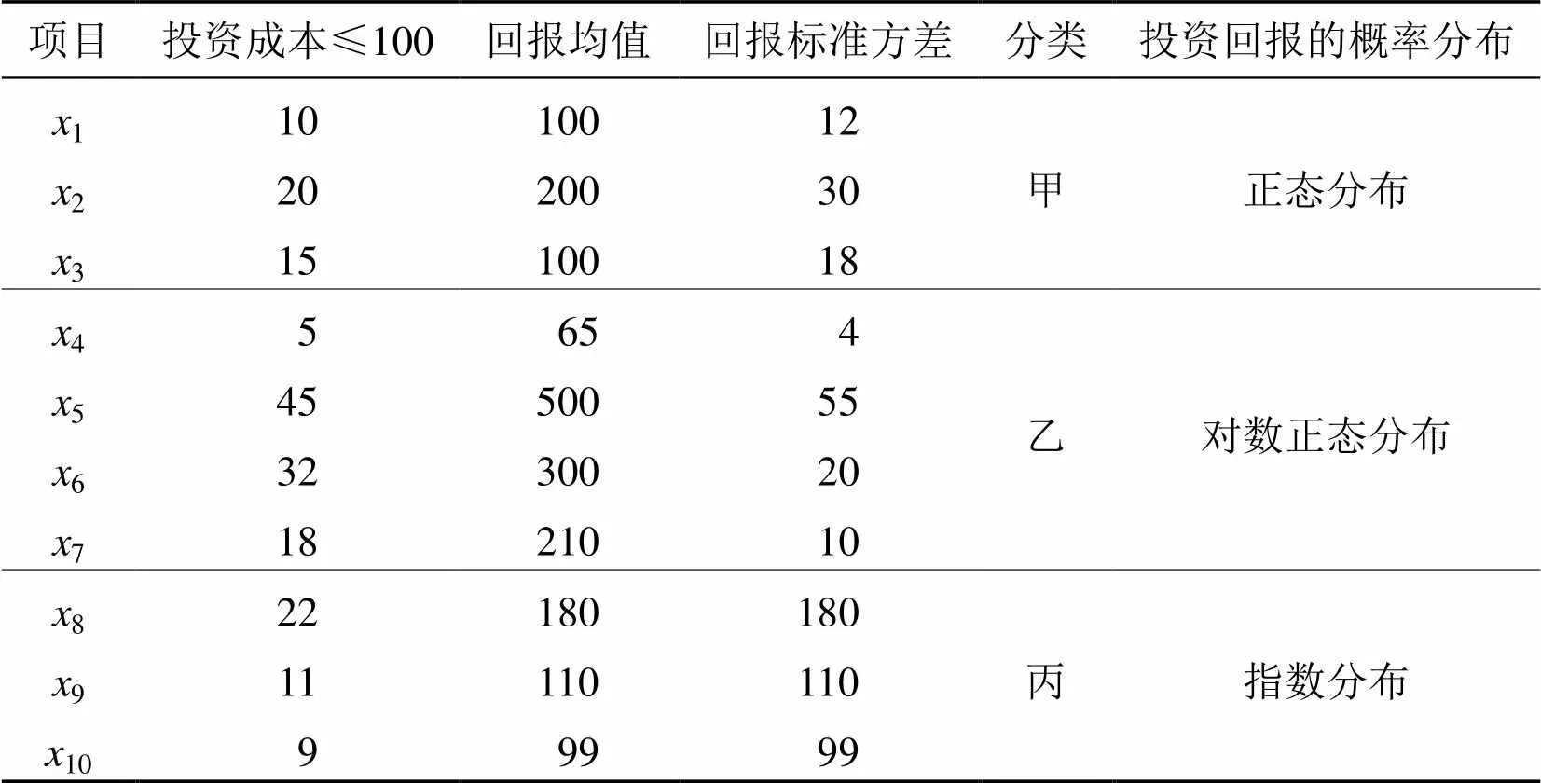
表1 项目设置要求表

表2 禁忌模拟算法计算进程输出表

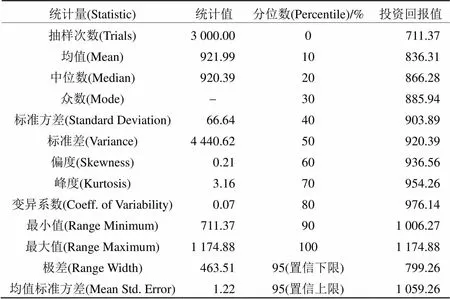
表3 禁忌模拟算法模拟结果各统计量输出表

设现有甲、乙、丙项目, 整体投资为100, 成本、回报概率散布于多个项目之中, 投资回报的概率分布为正态分布(1,2,3)、对数正态分布(4,5,6,7)、指数分布(8,9,10), 具体的个数需求见表1。假设决策者实际选择的极限期望值回报的组合要求有关的极限回报方差维持在120之下。在Excel中构建配套的模型, 同时利用禁忌模拟混合优化来获得所需的解, 挑选随机值的种子数为999, 同时运用拉丁超立方来实现总数为3 000次的抽样。最终通过该算法在进行11次循环时得到最优结论, 具体的模拟结论见表2、表3, 所能够获取的极限投资回报的95%置信区间维持在[799.26, 1 059.26]。

4 结论

本文考虑市场摩擦因子、交易成本及消费方面的支出问题、劳动方面的收入问题、投资方面的收益问题这3大不确定因素对于消费投资选择行为的影响, 分别给出了个体效用函数、劳动收入、跨期预算约束、投资机会及市场摩擦因素的数学表达方法。在此基础上, 考虑劳动收入风险、投资收益风险, 建立了消费投资组合动态优化模型。并通过实例阐明所提出模型能有效刻画实际市场中的消费投资情况, 所设计的算法是有效可行的。该方法充分考虑了金融市场中的摩擦因素, 为解决最优消费投资选择问题提供了新的思路, 具有较高的应用价值。

[1] Merton R C. Optimum consumption and portfolio rules in a continuous-time model [J]. Journal of economic theory, 1971, 3(4): 373-413.

[2] Karatzas I, Lehoczky J P, Sethi S P, et al. Explicit solution of a general consumption/investment problem [J]. Mathematics of Operations Research, 1986, 11(2): 261-294.

[3] Cox J C, Huang C F. Optimal consumption and portfolio policies when asset prices follow a diffusion process [J]. Journal of Economic Theory, 1989, 49(1): 33-83.

[4] Shreve S E, Soner H M, Xu G L. 1optimal Investment and Consumption with Two Bonds and Transaction Costs [J]. Mathematical Finance, 1991, 1(3): 53-84.

[5] Cuoco D, Cvitanić J. Optimal consumption choices for a ‘large’ investor [J]. Journal of Economic Dynamics and Control, 1998, 22(3): 401-436.

[6] Campbell J Y, Viceira L M. Consumption and portfolio decisions when expected returns are time varying [R]. National Bureau of Economic Research, 1996.

[7] Chacko G, Viceira L M. Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets [J]. Review of Financial Studies, 2005, 18(4): 1 369-1 402.

[8] Wan S. Stochastic Control in Optimal Portfolio with Regime Switching Model [C]//Control, Automation, Robotics and Vision, 9th International Conference on IEEE, 2006: 1-4.

[9] 费为银. 考虑红利支付的最优消费投资模型研究[J]. 安徽机电学院学报, 1997, 12(4):62-67.

[10] 丁传明, 邹捷中. 考虑随机收入和红利支付的最优投资消费模型研究[J]. 长沙铁道学院学报, 2003, 21(1): 93-96.

[11] 费为银, 吴让泉. HJB方程受约束粘性解的一个比较定理[J]. 系统科学与数学, 2001, 21(2): 198-203.

[12] 刘海龙, 吴冲锋. 考虑随机方差的最优消费和投资决策问题[J]. 管理工程学报, 2002, 16(1): 47-50.

[13] 杨昭军, 师义民. 最优投资及最优消费策略[J]. 高校应用数学学报(A辑), 1994(1): 90-95.

[14] 郭文旌. 跳跃扩散股价的最优投资组合选择[J]. 控制理论与应用, 2005, 22(2): 171-176.

[15] 肖建武, 尹少华, 康文星. 常方差弹性模型下的最优投资消费解析策略[J]. 统计与决策, 2007(3): 19-20.

[16] 杨芳. 证券投资组合和消费选择的最优控制问题[D]. 大连: 大连理工大学, 2005.

[17] 王康宁. 最优控制的数学理论[M]. 北京: 国防工业出版社, 1995.

[18] 刘海龙, 吴冲锋. 考虑随机方差的最优消费和投资决策问题[J]. 管理工程报, 2002, 16(1): 47-50.

(责任编校:刘晓霞)

Research of consumption and investment decision model based on Monte Carlo

Liu Huan

(College of Business Administration, Hunan International Business Vocational College, Changsha 410200, China)

With the consumption and investment in a cross-time optimization framework, a consumption investment decision model based on Monte Carlo risk assessment is proposed. First, the mathematical expressions of individual utility function, labor income, cross period budget constraints, investment opportunities and market friction factors are established. Then, taking into account the risk of labor income and investment income, the dynamic optimization model of consumption investment portfolio is set up. Finally, a practical example is discussed to illustrate effectiveness and practicability of the proposed model.

consumption investment decision; market friction factor; Monte Carlo; risk assessment

10.3969/j.issn.1672–6146.2016.04.003

O 174.5; O 177.2

1672–6146(2016)04–0006–05

刘欢, csuliuhuan@126.com。

2015-12-10

湖南省哲学社会科学规划基金办公室(13YBB158); 湖南省教育科学“十二五”规划课题(XJK014BZY021)。