0-1混沌测试算法中振幅对混沌序列的影响

熊绪沅, 万丽, 2, 赖佳境



0-1混沌测试算法中振幅对混沌序列的影响

熊绪沅1, 万丽1, 2, 赖佳境1

(1.广州大学数学与信息科学学院, 广东广州, 510006; 2. 广州大学数学与交叉科学广东普通高校重点实验室, 广东广州, 510006)

0-1混沌测试法是根据线性增长率()值是否趋近于1或0来判断离散数据混沌性的新方法。选取Verhulst种群模型生成的3类时间序列(弱混沌、完全混沌、4-周期)为研究对象, 验证了0-1测试法的有效性, 对0-1测试算法中振幅作了进一步探讨。结果表明: 弱混沌序列()值对振幅最敏感, 其次分别是强混沌序列和周期序列,()值随振幅变化的快慢可以反映序列的混沌程度。

0-1测试算法; Verhulst种群模型; 混沌识别; 噪声序列

混沌是指在确定性系统中出现的一种貌似无规则的类似随机的现象, 它不是简单的无序, 表面上没有明显的周期和对称, 但却是具有丰富的内部层次的有序结构, 是非线性系统的一种新的存在形式[1]。混沌系统的最大特点就是对演化的初始条件十分敏感, 因此, 从长期意义上讲, 系统的未来行为是不可预测的。混沌时序分析是混沌和时序分析相互渗透的一门学科。自20世纪90年代以来, 混沌时序分析在股票预测、脉冲控制、水文预报、DNA序列分析、水下目标识别、矿化识别等方面都有较成功的应用[2-8]。鉴别时间序列是否具有混沌吸引子存在, 是研究其混沌性的首要任务。目前, 常用的混沌识别方法主要有: 相图法、频谱分析法、庞加莱映象法、K熵法和Lyapunov指数法等。但这些混沌识别方法均存在一定的适应范围和局限性[9-10], 如相图法简单直观, 但精确度不高; 频谱分析法对受到噪声影响的序列很难从其频谱上区分其运动模式; 庞加莱映象法不能区分混沌和完全随机运动; 最大Lyapunov指数法的计算结果并非直接得到, 延迟时间和嵌入维数的确定具有一定的主观性和不确定性。

0-1测试法是一种不需要相空间重构, 直接通过计算离散数据转化变量的线性增长率()值是否趋近于1或0快速判断混沌是否存在的方法。Gottwald等[11-13]对用于含噪声序列的0-1算法中振幅该如何选择、怎样区分混沌的程度并没有详细讨论。本文以Verhulst种群增长模型生成的离散序列为研究对象, 验证0-1测试法对混沌识别的有效性和抗噪性, 给出3种不同性质序列(弱混沌、强混沌­、4-周期)的0-1测试图, 对该算法应用于含噪声序列时振幅对()值的影响作了进一步讨论。

1 0-1混沌识别算法

如果离散时间序列为非混沌的, 如周期的或倍周期的,p()-q()的轨迹图有界稳定; 如果离散时间序列是混沌的,p()-q()轨迹图近似布朗运动。傅里叶变换原理与式(1)和(2)原理不同: 傅里叶变换把时间序列从时间域变换到频率域, 离散的信号频率域对应着周期的时间序列, 周期的信号频率域对应着离散的时间序列, 进而研究信号的频率结构和变化规律[14]。

第2步, 计算p()和q()的均方位移函数值D(),

第3步, 计算D()随的线性增长率(), 即取D()与的相关系数

文献[13]针对序列中含有噪声的情况, 提出了修正方法, 即算法中第1、3步不变, 第2步变为计算p()和q()的修正均方位移函数值,

振幅用来控制0-1测试法对弱噪声和弱混沌的敏感性, 式(5)中D()与式(3)保持一致。文献[13]对振幅该如何选择并没有详细说明, 通常只选取了振幅= 2.5的情形。

2 0-1测试法有效性检验

为验证0-1测试法的有效性, 选取Verhulst种群模型迭代序列为研究对象, 种群模型迭代公式为

其中,为种群增长因子。根据不动点定理可知, 在[0, 2]中式(6)有稳定的不动点1。对[1.8, 3.0], 利用Matlab模拟生成500个对应的迭代序列, 其分岔图形如图1所示。同时以增长因子为横坐标, 间距为0.001, 对每个生成数据长度= 2 000的离散序列, 代入不含噪声0-1测试算法计算出对应的()值为纵坐标, 作出Verhulst种群模型迭代序列的—()图如图2所示。

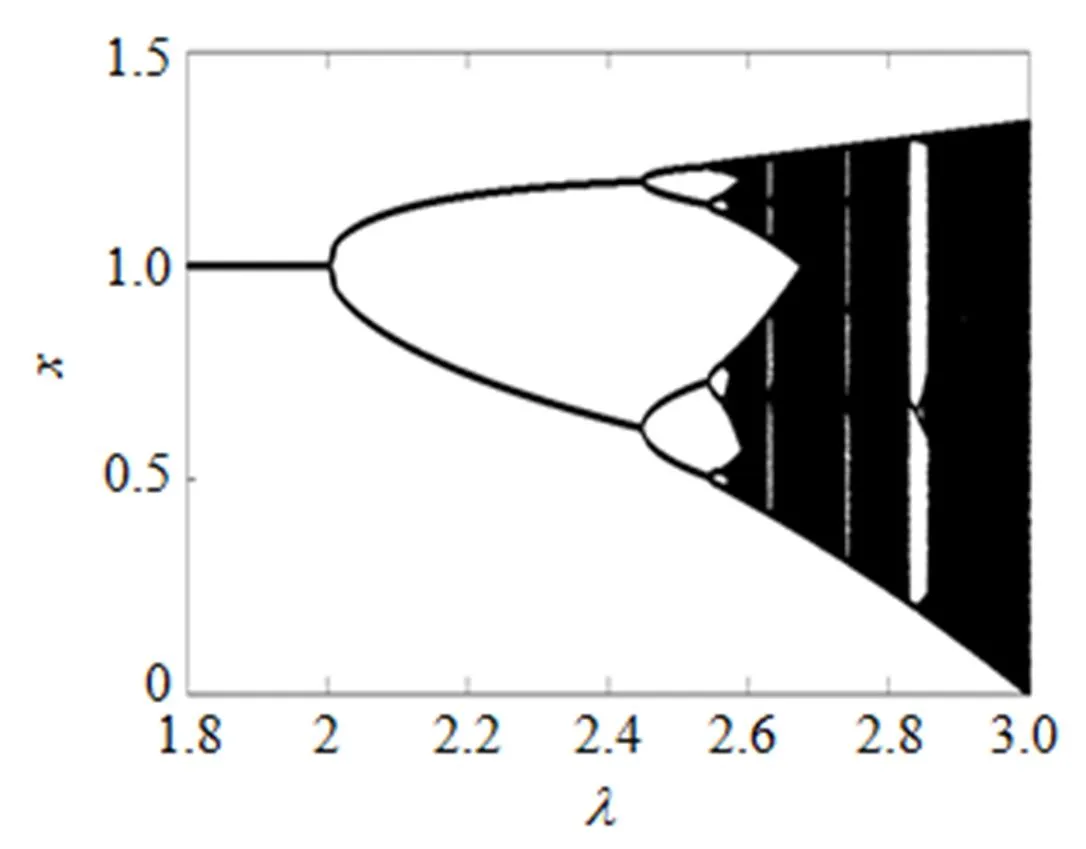
图1 Verhulst模型分岔图

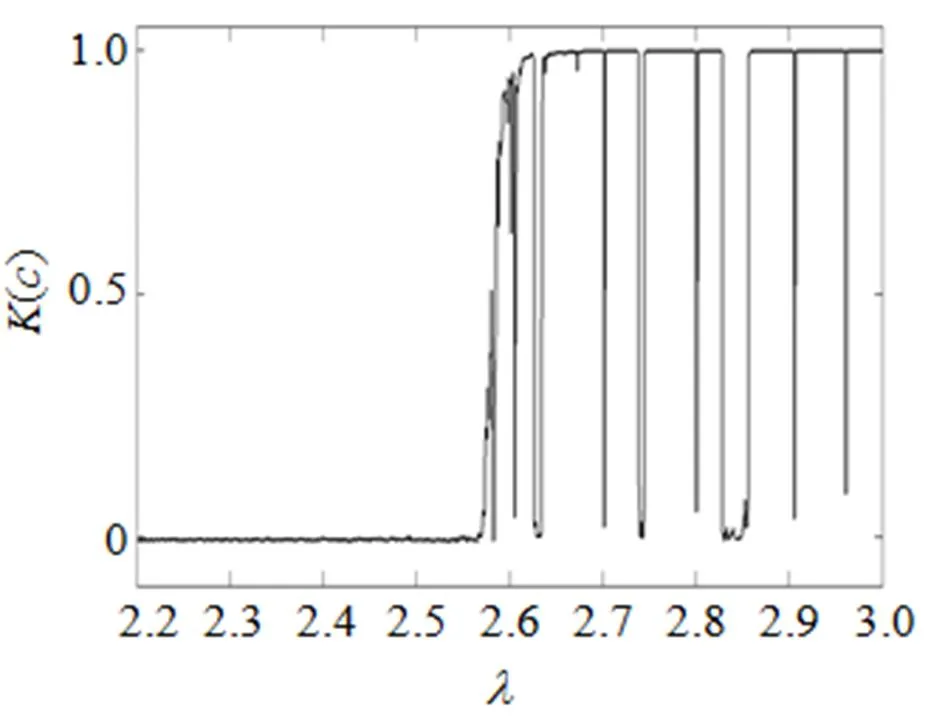
图2 Verhulst模型λ—K(c)图

对比图1和图2可知: 当Verhulst序列为周期序列时, 对应的()值趋于0; 当Verhulst序列由周期通向混沌状态时,()值由0上升为1; 当序列为混沌序列时, 对应的()值趋于1。图2中Verhulst序列的0-1测试值反映的状态与图1中Verhulst序列的分岔图状态相吻合, 验证了0-1测试法的有效性。少数点()值突然由1变为0, 部分的取值出现了频率共振现象, 并不影响0-1测试法的整体有效性。

图3(a, b, c)分别给出了= 2 000,= 2.576 3 (弱混沌),= 2.990 0 (强混沌)和= 2.500 0 (4-周期)的—(= 1.8)轨迹图,M()—和()—散点图。由图3可知:= 2.576 3时, 系统为弱混沌状态,—轨迹图出现由有界走向杂乱的现象,M()—图类似正弦函数图像,M()值介于0和3.5之间,()—图中()的值稳定在0.18附近;= 2.990 0时, 系统为完全混沌状态,—图表现为近似布朗运动,M()随线性增长,()值趋近于1;= 2.5时, 系统为4周期状态, 此时—轨迹图有界稳定, 图像出现4个同心圆, 这与系统为4周期相符,()值分布在0附近,M()值分布散乱。说明0-1测试图能够很好地反映序列是否具有混沌性。

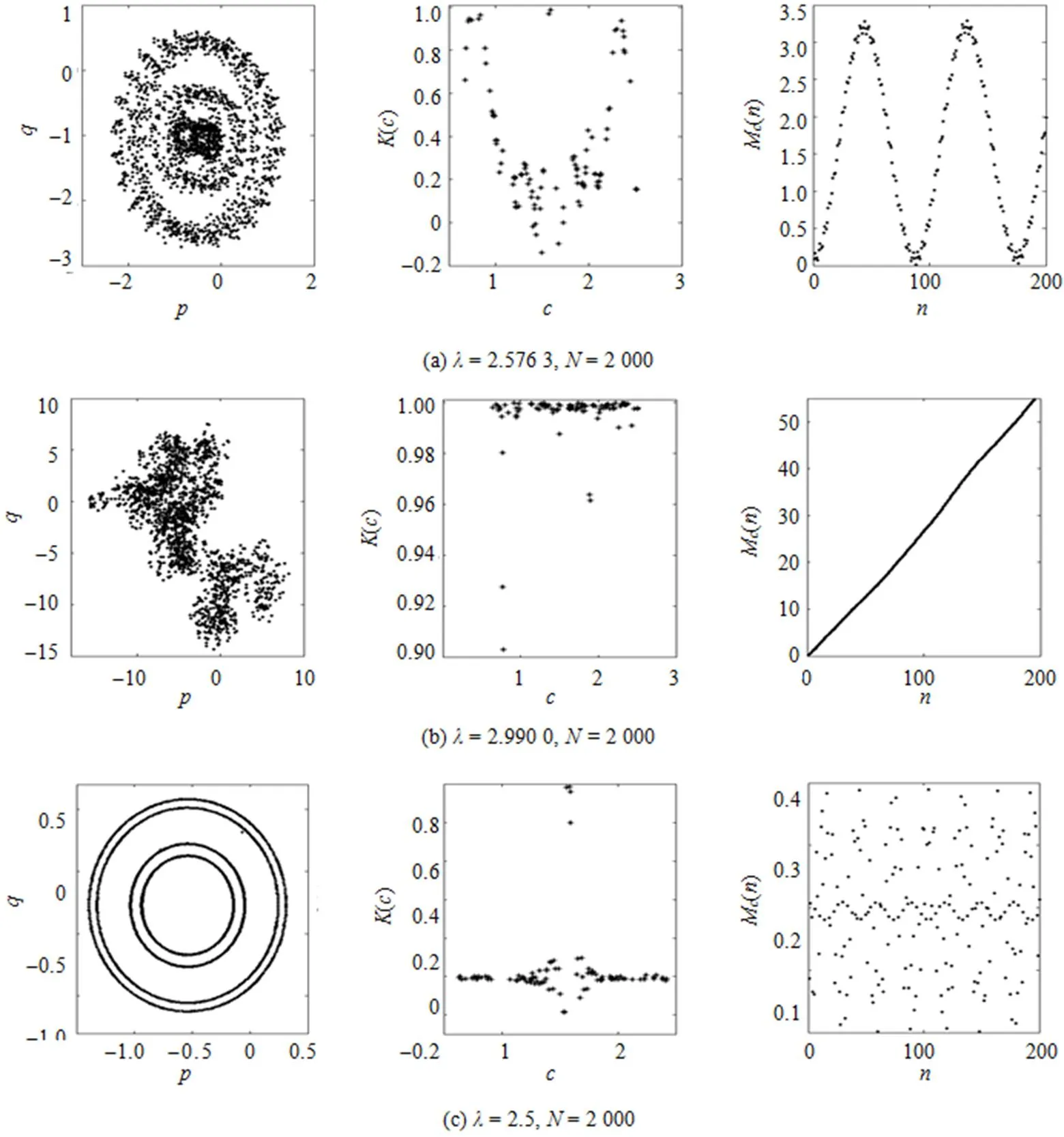
图3 Verhulst序列的0-1测试图

3 振幅对0-1测试法的影响

实际数据不可避免含有一定程度的噪声, 为提高测试的可靠性, 此时应选用含振幅的0-1测试算法来计算线性增长率()。设(= 1, 2, …,)为原始Verhulst序列, 加入噪声后生成的时间序列为

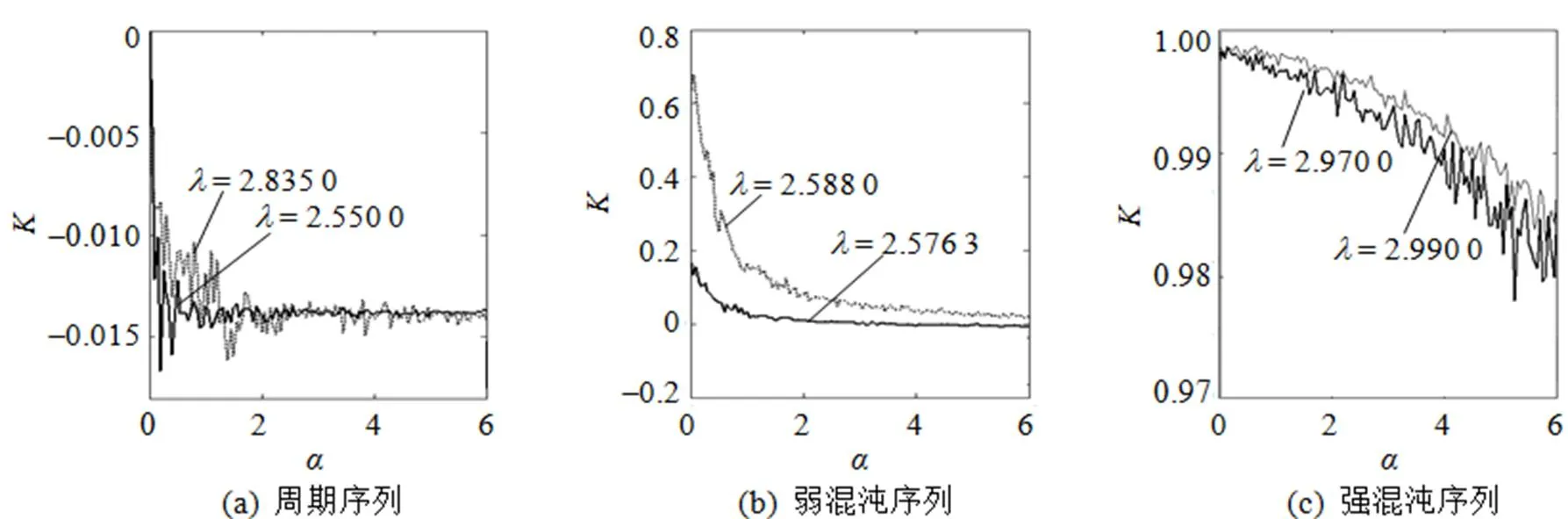
图4 含噪水平为5%的Verhulst序列K—α图

由图4可知在添加强度为5%的噪声后, 3种不同性质序列的()值均下降, 但下降幅度不一样,—图呈现出不同特征。随着振幅的不断增大, 周期序列()降幅最小, 基本稳定在0附近; 弱混沌序列()值降幅最大, 对振幅最敏感, 混沌性越弱, 曲线下降越快, 在= 4.5时,()值已经降至0.05以下; 完全混沌序列的()值下降相对缓慢,达到6.0时()值保持在0.9以上。3种不同性质序列的—图呈现不同的变化趋势, 可从序列—图的特征来判断序列是否具有混沌性: 序列—图中()值始终稳定在0附近, 则序列为周期序列;—图中()值随振幅的增加迅速向0靠拢, 则序列为弱混沌序列, 混沌性越弱,()值下降越快;—图中()值随振幅缓慢下降后能维持在0.9附近, 则序列为强混沌序列。不同性质序列的—图的不同表现特征可为实际数据的混沌判别提供参考, 对实际数据选用含振幅的0-1测试法并结合—图可以进一步提高混沌判别的准确性。

4 结论

选取Verhulst种群模型迭代序列为研究对象, 通过对比原始Verhulst序列的分岔图和0-1测试—()图, 作出3类不同性质(弱混沌、强混沌、4-周期)序列的0-1测试图, 验证了0-1测试算法的有效性, 探讨了算法中振幅对含噪水平为5%的3种不同性质Verhulst序列的影响。得出如下结论: 0-1测试算法具有一定抗噪性, 从—图中可以区分混沌的强弱性, Verhulst序列的0-1测试—图和其分岔图所反映的系统状态相吻合, 周期序列时()值趋近于0, 混沌序列()值趋近于1, 0-1测试法能有效识别序列的混沌性; 对3组含噪水平为5%的Verhulst序列的—图研究发现, 周期、弱混沌和强混沌序列的()值对振幅敏感程度不一样, 弱混沌序列最敏感, 其次分别是强混沌序列和周期序列, 混沌性越强,()值随振幅下降越缓慢, 可以从—图中曲线下降的快慢来区分序列混沌性的强弱。

[1] Schuster H G, Just W. Deterministic chaos: an introduction [M]. Weinheim: Wiley-VCH Verlag GmbH & Co KGaA, 2005: 1-7.

[2] 朱华, 姬翠翠. 分形理论及其应用[M]. 北京: 科学出版社, 2011: 207-221.

[3] 邹琳, 杨亚男, 马超群. 股票市场混沌演化机制: 基于计算实验方法的模拟解释[J]. 系统工程, 2013, 31(7): 8-14.

[4] 刘东兵, 李阳. Lur’e混沌系统的脉冲控制同步[J]. 湖南文理学院学报(自然科学版), 2008, 20(3): 83-85.

[5] Wang S,Huang G H, Baetz B W, et al. A polynomial chaos ensemble hydrologic prediction system for efficient parameter inference and robust uncertainty assessment [J]. J Hydrol, 2015, 530: 716-733.

[6] Stan C, Cristescu C P, Scarlat E I. Similarity analysis for DNA sequences based on chaos game representation, Case study: The albumin [J]. J Theor Biol, 2010, 267(4): 513-518.

[7] 杨德森, 肖笛, 张揽月. 水下混沌背景中的瞬态声信号检测法研究[J]. 振动与冲击, 2013, 32(10): 26-30.

[8] 万丽, 刘欢, 杨林, 等. 成矿元素巨量聚集的混沌机制—斑岩型和构造蚀变岩型矿床例析[J]. 岩石学报, 2015, 31(11): 3 455-3 465.

[9] Pellicano F, Vestroni F. Nonlinear dynamics and bifurcations of an axially moving beam [J]. J Vib Acoust, 2000, 122(1): 21-30.

[10] Riedel C H, Tan C A. Coupled forced response of an axially moving strip with internal resonance [J]. Int J Nonlin Mech, 2002, 37 (1): 101-116.

[11] Gottwald G A, Melbourne L. A new test for chaos in deterministic systems [J]. Proc R Soc Lond A, 2004, 460: 603-611.

[12] Gottwald G A, Melbourne L. Testing for chaos in deterministic systems with noise [J]. Physica D, 2005, 212(1/2): 100-110.

[13] Gottwald G A, Melbourne L. On the implementation of the 0-1 test for chaos [J]. SIAM J on Appl Dyn Syst, 2009, 8(1): 129-145.

[14] 胡广书. 数字信号处理[M]. 北京: 清华大学出版社, 2003: 127-173.

(责任编校:刘晓霞)

Influence of amplitude on chaos sequence in the 0-1 test algorithm

Xiong Xuyuan1, Wan Li1, 2, Lai Jiajing1

(1. School of Mathematics and Information Sciences, Guangzhou University, Guangzhou 510006, China; 2. Interdisciplinary Sciences of Guangdong Higher Education Institutes, Guangzhou University, Guangzhou 510006, China)

The 0-1 test method is a new method which through the determining discrete data transformation variable’s linear growth rate() approaches to 1 or 0 to judge whether discrete time series are chaotic or not. Selecting three kinds of time series (weak chaos, strong chaos and 4 period-doubling) generated by classic Verhulst population model as the research object, the validity of the 0-1 test method is verified, and the amplitudeof the 0-1 test algorithm is further discussed. The results show that the() value of weak chaotic sequence is the most sensitive to the amplitude, followed by the strong chaotic sequence and the periodic sequence, the speed of decline of() value changes with the amplitude can reflect the degree of chaos.

0-1 test algorithm; Verhulst population model; chaos identification; noised sequence

10.3969/j.issn.1672–6146.2016.04.008

O 415.5

1672–6146(2016)04–0035–05

熊绪沅, 1262839457@qq.com。

2016-05-19

国家自然科学基金项目(41172295)。