基于重构方案线路投运风险最小的机组恢复顺序优化

王江宇，刘 艳



基于重构方案线路投运风险最小的机组恢复顺序优化

王江宇，刘 艳

(华北电力大学电气与电子工程学院, 河北 保定 071000)

电力系统大停电后，合理有序的恢复控制对于减小停电损失具有重要意义。以架空线路投运作为研究重构过程的切入点，提出了利用线路投运可靠性指标优化机组恢复顺序的方法。首先，针对当前重构方案线路投运风险定义的不足，提出了与停电损失评价标准相一致的严重程度指标。其次，通过网架恢复与机组投运过程的交互仿真，建立了与恢复实际更加契合的重构模拟时步框架。在此基础上，构建了以重构方案线路投运风险最小为目标的机组恢复顺序优化模型，并采用交叉粒子群算法和弗洛伊德算法对模型进行优化求解。针对新英格兰10机39节点系统的仿真结果表明，采用该方法获得的机组恢复方案在降低停电损失的同时，充分考虑可能的恢复路径备用通道，能够更加有效地应对潜在的线路投运失败情况。

大停电；网架重构；重构方案线路投运风险

0 引言

大停电后的电力系统恢复是一个复杂的决策和控制问题，其恢复过程根据恢复目标和任务的不同，通常被分为黑启动、网架重构和负荷恢复三个阶段[1]。其中，网架重构阶段的主要目的是充分利用黑启动电源及已经恢复的发电容量，依次启动重要机组并投入主要的输电线路，逐步建立起稳定的骨架网络，为下一阶段负荷的全面恢复奠定基础。如何确定恢复的目标骨架网络及其恢复路径序列是该阶段的主要任务[2-7]。

针对恢复路径优化方面的研究已取得一定成果。文献[8]将系统网架重构阶段分为“串行”和“并行”两类，根据不同的求解方法，得到最优恢复路径。文献[9]综合考虑开关操作次数和网络损耗2个经济性因素，建立计及电网经济性的多目标恢复重构模型，并从群体模型和遗传算子的角度，提出了一种供电恢复重构遗传寻优算法，寻求最佳方案。文献[7]综合考虑节点有功发电出力、有功负荷大小以及网络拓扑结构，得到最优的恢复路径序列和目标骨架网络。文献[10]以系统可发电容量最大、恢复路径的平均重要度最大和路径充电电容最小为目标进行优化。文献[11]以网络重构时间和机组出力恢复程度为目标，优化目标节点的恢复顺序。文献[12]综合考虑负荷恢复代价、负荷性质、负荷重要性及负荷恢复对后续网架重构的影响，优化网架重构恢复序列。但以上研究仅以技术指标进行评估，实际上，在恢复供电的过程中，由于自然和气象条件，以及人为因素等的影响，线路存在投运失败的可能性，因此有必要从线路投运可靠性角度进行评估。目前，在电力系统可靠性方面的研究很多[13-16]，关于线路投运可靠性方面，文献[17]以目标节点的恢复成功率作为选择恢复路径的标准，文献[18]将线路投运可靠性作为多目标优化中的一个目标，指导最优方案的生成，但线路恢复操作可靠性仅以各条路径成功恢复的概率表示，没有兼顾线路投运失败对系统恢复效果的影响。针对以上缺点，文献[19]定义了线路投运风险的概念来全面评价线路恢复操作的可靠性，但以线路的充电电容和倒闸操作的次数等静态参数作为线路投运失败的相对可能性，最终求得的线路投运风险为固定值，不能反映线路投运风险随时间的变化过程。文献[20]克服这一缺点，采用两状态马尔科夫模型，模拟不确定因素对线路投运过程的影响，建立采用模糊修复率和统计故障率的线路投运模型，得到网架重构的不同时刻，已投运线路停运的可能性，进一步完善线路投运风险的求取过程。但其也存在明显不足。首先，其关于线路投运失败的严重程度仅以恢复机组的数量、恢复路径的权值等参数来衡量，与大停电后系统恢复过程风险评价标准并不相符；其次，文献[20]在求取线路投运失败的概率时，假设线路经固定时间间隔投运，不符合实际系统恢复过程中线路的投运情况，不能准确地反映投运过程中风险的变化。此外，文献[20]仅针对不同重构方案的线路投运风险进行评价和比较，并没有以方案的线路投运风险为优化目标引导最优重构方案的生成。

综上所述，本文将线路投运风险的严重程度重新定义，统筹考虑线路投运失败后转移路径下系统的失负荷量和停电时间对恢复效果的影响，将线路投运失败的严重程度与大停电后风险的评价标准统一起来。此外，通过模拟网架重构过程获得各线路的具体投运时间，进一步完善线路投运风险的求取过程。最后，以方案的线路投运风险最小为优化目标，采用交叉粒子群和弗洛伊德算法，求得最优的系统网架重构机组恢复顺序。

1 线路投运风险

IEEE标准100-1992将风险定义为对不期望发生的结果的概率和严重性的度量，通常采用概率和后果乘积的表达形式[21-23]。故定义风险指标为事故可能性与事故后果严重程度的乘积。1999年，美国衣阿州立大学的Vittal、Mc Caley等人成功地将风险理论应用于电网运行安全评估中，来解决电网可靠性的问题，为电网可靠性的评估提供了方法。本文利用线路投运风险指标评价线路投运可靠性，指导最优方案的生成。

1.1 线路投运风险的严重程度

为示意线路投运失败对系统失负荷量和停电时间(即恢复供电的时间)带来的影响，首先以图1所示的新英格兰10机39节点系统的某一恢复方案为例进行分析。其中33号机组为黑启动机组，其余机组为待恢复的火电机组。额定容量、状态转移率等参数见文献[24]。停电前，系统发电总量为3605.03 MW；大停电后，选定机组恢复顺序33-32-35-38-37- 39-30-34-31-36进行说明。若所有线路顺利恢复，其恢复路径顺序如表1中“顺利投运路径”所示。若在恢复机组38时，线路16-17投运失败，则会以已经恢复带电的初期小系统(图1中加粗区域)为起点，寻找至机组38的转移路径。转移路径建立14- 4-3-18-17供电通道以弥补16-17投运失败的影响，这使得恢复机组38所需的时间由原来的0.892 2 h延长到4.961 4 h，大大延长了恢复供电时间。将上述两种情况分别绘制成失负荷时间曲线，如图2所示。虽然在所有机组投运完成后系统总的失负荷量差异不大，但线路投运失败造成的恢复进程延误却是相当严重。

根据文献[25]，系统失负荷量和停电时间与大停电的损失直接联系。因此，本文采用系统失负荷量和停电时间的乘积来衡量特定重构恢复序列的恢复效果，其物理意义为系统失电量，如式(1)所示。

表1顺利投运和转代恢复的恢复信息一览

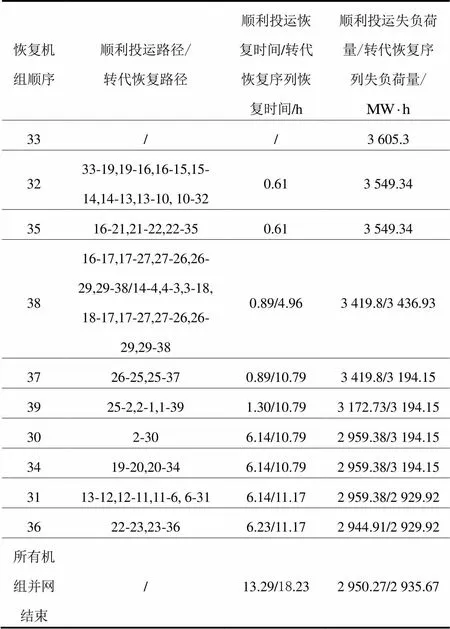
Table 1 Review of details corresponding to restoration without and with transfer paths

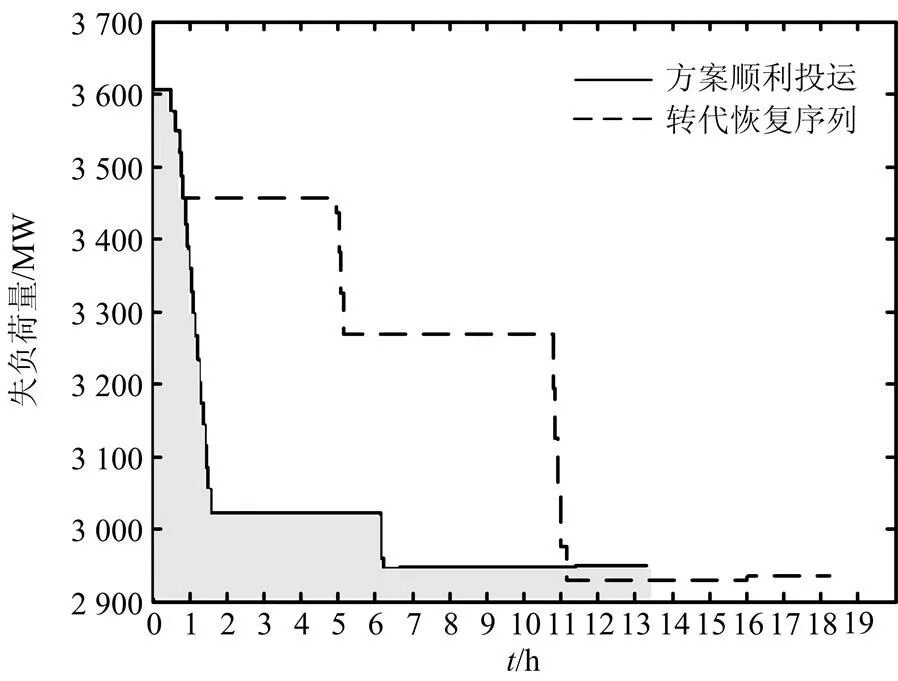
图2 顺利投运和转代恢复的失负荷时间曲线对比

1.2 线路投运风险的可能性

对于线路投运风险的可能性，即线路投运失败概率的求取，本文依然采用文献[20]的方法。以马尔科夫两状态模型为基础，考虑空载线路合闸失败或合闸成功后出现的停运情况等不确定因素，在任意时刻线路处于运行或停运两种状态下的概率如式(3)所示。

1.3 线路投运风险

根据风险指标，定义各条线路的投运风险为该线路投运失败的可能性和该线路投运失败对重构操作影响的综合度量[19]。线路投运失败的可能性和该线路投运失败对重构操作的影响已经量化并求出，线路在时刻的线路投运风险定义如式(4)所示。

2 基于恢复方案线路投运风险最小的机组  恢复顺序优化

以恢复方案线路投运风险最小为优化目标，选取合理的方法预选黑启动机组和线路，通过对大量方案的分析和比对，最终找出综合考虑线路恢复技术效果和可靠性的最优机组恢复顺序。本文采用交叉粒子群和弗洛伊德算法优化。

2.1 恢复方案线路投运风险

线路投运风险的求取过程上节中已经明确介绍。恢复过程中，各线路均存在投运失败的可能性，方案的线路投运风险定义见式(5)。

2.2 基于恢复方案线路投运风险最小的机组恢复顺序优化

为了得到线路投运可靠性高的恢复序列，保证线路投运失败后造成的损失最小，利用恢复方案线路投运风险指标优化机组恢复顺序。采用交叉粒子群算法实现机组恢复顺序的排序；采用弗洛伊德算法求解带电区域到目标节点的最优路径和转代恢复路径。

交叉粒子群算法主要采用文献[26]中的方法进行求取。从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质。最优方案适应度值如式(6)所示。

弗洛伊德算法以折算到同一电压等级下，支路的充电电容为权值，权值最短路径设为恢复路径。简便快捷的找出带电区域到目标节点间的最短供电路径，为停电后的恢复过程节省了时间。若线路投运失败没有转移通道，则假设等待相应时间，再通过该线路进行恢复。

3 算法的实现

利用恢复方案的线路投运风险这一指标指导最优方案的生成。首先以重构过程的模拟为基础，获得各时步长度和系统失负荷量，为线路投运风险的求取铺垫。

3.1 重构时步的长度

以文献[24]中机组建模过程的约束条件为模拟重构过程的约束条件。考虑到厂内机组恢复所需操作最为复杂且前导时间较长，并且，与其相关的变电站或线路的准备工作可同时进行，在有机组出力的情况下，以某时步内的机组恢复时间近似作为重构时步的长度。采用保定太维计算机技术开发有限公司针对实际典型机组研制开发的火电机组启动及升负荷仿真程序完成对机组恢复时间的统计。当某时步仅有一台机组增发功率时，调用该程序求得达到目标负荷所需时间并与当前时刻比较即可获得重构时步长度；当同时有多台机组在某时步增发功率时，依据前述方法计算与每台机组对应的净时长后，取其最大值作为该时步长度。以重构时步长度为基础，获得各线路的投运时间。

3.2 恢复方案线路投运风险的求取

综合式(1)至式(5)，得到恢复方案线路投运风险。其式(3)中各线路的投运时间，采用系统重构过程模拟获得的线路投运时间表示。

3.3 算法流程

基于恢复方案线路投运风险最小，采用交叉粒子群和弗洛伊德算法优化网架重构机组恢复顺序的流程图如图3所示。

4 算例分析

以新英格兰10机39节点系统为例验证本文方法的有效性。选定粒子数为10，迭代次数为100。以恢复方案的线路投运风险最小为目标，得到最优恢复顺序为33-39-32-35-38-36-30-31-34-37，如表2所示。此外，表2还统计了该方案恢复过程中各线路的具体停运时间和相应时间下方案的线路投运风险。

从表2可以看出，随着时间的增加，方案的线路投运风险呈下降趋势，原因有两点：就线路投运风险的可能性而言，随着时间的增加，已投运线路数量增加，由于未投运线路投运失败的概率为1，远远高于已投运线路，故方案的线路投运风险逐渐降低；就线路投运风险的严重程度而言，随着时间的增加，已投运线路数量增加，网架结构逐渐趋于坚强，线路停运造成的影响变小，故方案的线路投运风险降低。此外，从表2还可以看出，0.65 h前没有线路投运，方案的线路投运风险高。0.65 h后，线路开始陆续投运，方案的线路投运风险逐渐降低。1.58 h开始投入机组30，之后由于潮流不收敛、带电区域规定时间内发出的电量不能带动下一机组启动等原因造成线路投运迟滞，需要等待至下一时步新的机组并网再重新校验，直到4.69 h满足所有约束条件再进行投运，并有大量线路同时投运，故方案的线路投运风险值骤降。另外，从表2的模拟结果还可看出，线路顺序投运的时间间隔并不固定，时间的长短主要取决于机组恢复和接带负荷的速度。

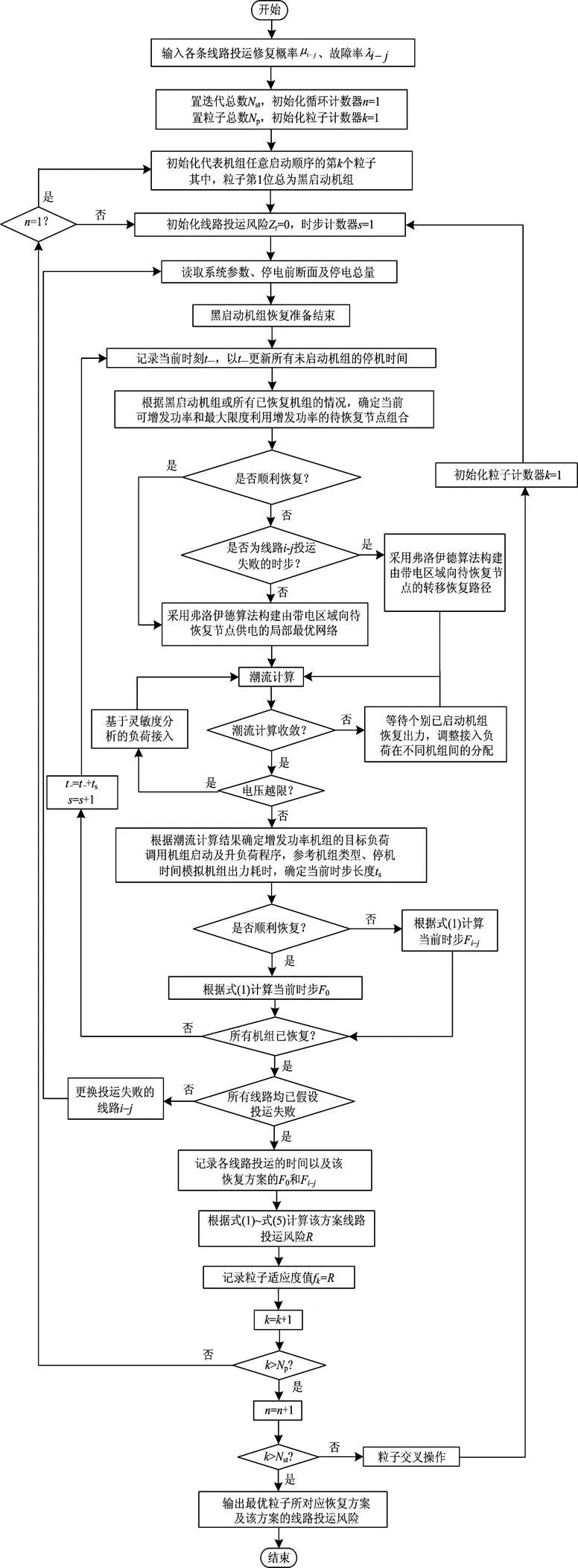
图3 基于方案线路投运风险最小优化机组恢复顺序流程图

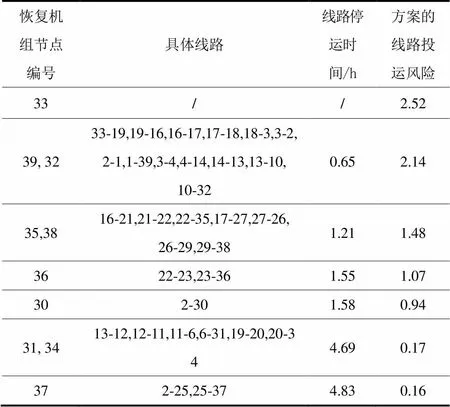
表2 最优恢复顺序相关信息一览

以恢复方案的线路投运风险最小为优化目标，得到效果较优的三套恢复方案，其方案的线路投运风险变化如图4所示，具体机组恢复顺序和恢复效果对比如表3所示。

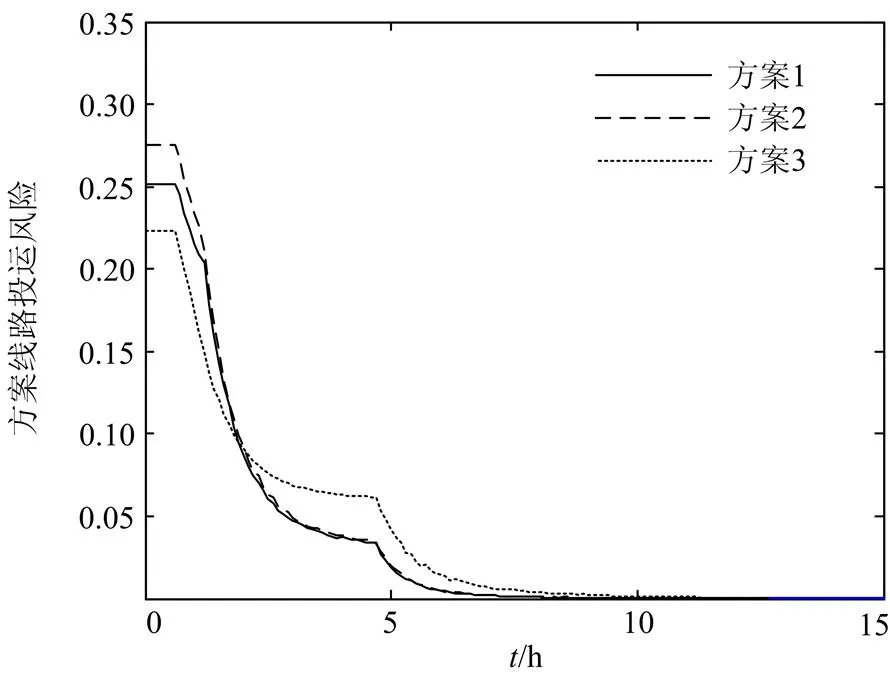
图4最优及次优方案线路投运风险变化曲线

从图4可以看出，不同方案在初始时刻线路投运风险不同，因为不同恢复预案所形成的网架结构各异，各条线路投运失败对系统恢复效果的影响不同，导致各条线路投运风险的差异。且不同恢复方案经过的线路数量不同，故方案的线路投运风险不同。

表3最优及次优方案恢复效果对比

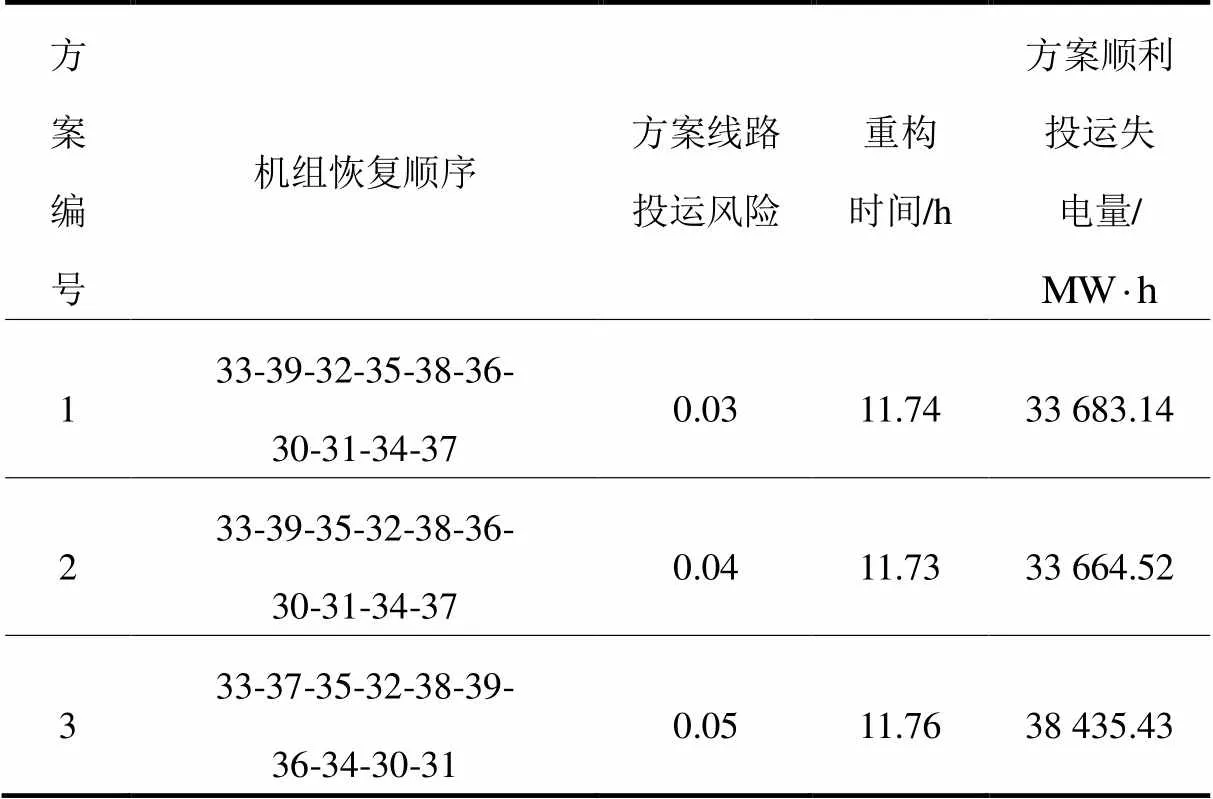
Table 3 Comparison of the optimal and suboptimal restoration schemes

方案1所形成的网架结构，线路投运失败对系统恢复效果的影响较小，方案线路投运风险起点较低，投运过程相对顺利，风险下降速度快，恢复时间短，故方案的线路投运风险低。方案3初始时刻的线路投运风险低于方案2，但投运过程中由于潮流不收敛等原因，造成方案线路投运风险在某水平持续一段时间，故下降速度低于方案2，方案线路投运风险高于方案2。

若不考虑线路投运可靠性，仅以重构结束时刻系统失电量最小为优化目标，得到的最优和次优恢复顺序与本文中最优和次优恢复顺序对比如表4所示。其中，方案1和方案2分别为本文最优和次优方案，方案3和方案4分别为以系统失电量最小为目标优化的最优和次优方案，其方案线路投运风险曲线如图5所示。

图5中，方案3和方案4趋势大致相同，以方案4为例进行分析，除黑启动电源外，机组34首先进行恢复，经过线路为33-19,19-20,20-34。三条线路投运失败均没有备选路径给机组34供电，系统将损失机组34的全部发电量，需等待一定时间重新为机组34供电，故线路投运失败对系统恢复的影响较大，方案线路投运风险较高。方案1和方案2趋势大致相同，以方案2为例进行分析，除黑启动电源外，机组39首先进行恢复。经过线路为33-19,19-16,16-17,17-18,18-3,3-2,2-1,1-39。八条线路中6条有备选恢复路径，投运失败后通过转移恢复路径为机组39供电，系统损失电量小，不用等待时间恢复，风险相对较小，待系统网架结构相对稳定，再对没有备选方案的线路进行恢复。故线路投运失败对系统恢复的影响较小，方案线路投运风险较低。综上，仅从失电量的角度出发预选方案，并没有考虑线路投运失败带来的严重后果，在恢复初期恢复了多条无备用路径的关键线路，一旦投运失败，对系统恢复效果的影响很大，因此线路投运初期风险值较高。

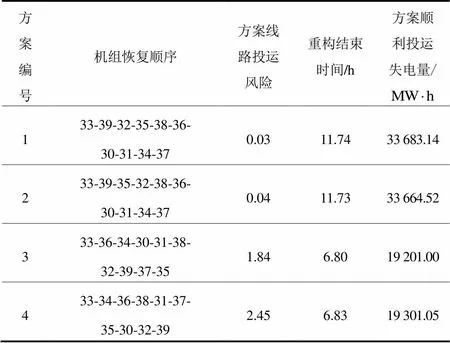
表4 本文较优方案和以失电量最小为目标的较优方案对比

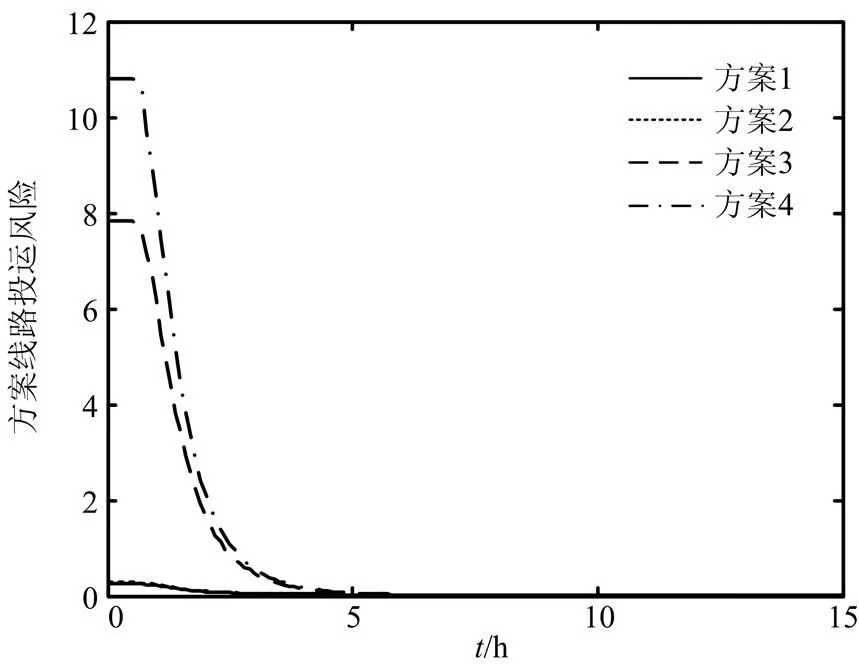
图5 本文较优方案和以失电量最小为目标的较优方案的线路投运风险比较

5 结论

本文针对黑启动网架重构阶段的机组恢复顺序进行优化。首先对传统线路投运风险的不足进行改进，采用系统失负荷量和停电时间共同表示投运失败的严重程度。然后，以模拟网架重构恢复过程所得到的线路具体投运时间代替以往假设的线路投运时间，完善线路投运失败概率的求取。最后，以恢复方案线路投运风险最小为优化目标，结合交叉粒子群和弗洛伊德算法，优化网架重构机组恢复顺序，指导最优方案的生成。以新英格兰10机39节点系统为例，得到线路投运可靠性高的方案。本文研究对于提高现代电力系统应对大停电事故的能力有指导意义。

[1] ANCONA J. A framework for power system restoration following a major power failure[J]. IEEE Transactions on Power Systems, 1995, 10(3): 1480-1485.

[2] 刘艳, 顾雪平. 基于节点重要度评价的骨架网络重构[J]. 中国电机工程学报, 2007, 27(10): 20-27.

LIU Yan, GU Xueping. Node importance assessment based skeleton-network reconfiguration[J]. Proceedings of the CSEE, 2007, 27(10): 20-27.

[3] 魏智博, 刘艳, 顾雪平. 基于DPSO算法以负荷恢复为目标的网络重构[J]. 电力系统自动化, 2007, 31(1): 38-42.

WEI Zhibo, LIU Yan, GU Xueping. DPSO algorithm based network reconfiguration of power systems for maximizing load recovery efficiency[J]. Automation of Electric Power Systems, 2007, 31(1): 38-42.

[4] WU J S, LIU C C, LIOU K L, et al. A Petri net algorithm for scheduling of generic restoration actions[J]. IEEE Transactions on Power Systems, 1997, 12(1): 69-76.

[5] PARK Y M, LEE K H. Application of expert system to power system restoration in sub-control center[J]. IEEE Transactions on Power Systems, 1997, 12(2): 629-635.

[6] 林振智, 文福拴. 基于加权复杂网络模型的恢复路径优化方法[J]. 电力系统及其自动化, 2009, 33(6): 11-16.

LIN Zhenzhi, WEN Fushuan. A new optimization method for determining restoration paths based on weighted complex network model[J]. Automation of Electric Power Systems, 2009, 33(6): 11-16.

[7] 谢夏慧, 汪沨, 卢鸣凯, 等. 大停电后初期基于分布式电源的配电网局部自我恢复方案[J]. 电网技术, 2013, 37(7): 1834-1840.

XIE Xiahui, WANG Feng, LU Mingkai, et al. A distributed generation-based local self-recovery scheme for distribution network at post-blackout early stage of power grid restoration[J]. Power System Technology, 2013, 37(7): 1834-1840.

[8] 周云海, 闵勇. 恢复控制中的系统重构优化算法研究[J]. 中国电机工程学报, 2003, 23(4): 67-70.

ZHOU Yunhai, MIN Yong. Optimal algorithm for system reconstruction[J]. Proceedings of the CSEE, 2003, 23(4): 67-70．

[9] 张巍, 孙云莲, 胡雯, 等. 计及电网经济性的配电网供电恢复重构寻优算法[J]. 电网与清洁能源, 2013, 29(7): 41-45.

ZHANG Wei, SUN Yunlian, HU Wen, et al. Optimized reconfiguration algorithm for power supply recovery of distribution network with economy of power grid considered[J]. Power System and Clean Energy, 2013, 29(7): 41-45.

[10] 张璨, 林振智, 文福拴, 等. 电力系统网络重构的多目标双层优化策略[J]. 电力系统自动化, 2014, 38(7): 29-38.

ZHANG Can, LIN Zhenzhi, WEN Fushuan, et al. A multiobjective bi-level optimization strategy for network reconfiguration of power systems[J]. Automation of Electric Power Systems, 2014, 38(7): 29-38.

[11] 刘艳, 高倩, 顾雪平. 基于目标规划的网架重构路径优化方法[J]. 电力系统自动化, 2010, 34(11): 33-37.

LIU Yan, GAO Qian, GU Xueping. Optimization of restoration sequence of network based on goal programming[J]. Automation of Electric Power Systems, 2010, 34(11): 33-37.

[12] 钟慧荣, 顾雪平, 朱玲欣. 黑启动恢复中网架重构阶段的负荷恢复优化[J]. 电力系统保护与控制, 2011, 39(17): 26-32.

ZHONG Huirong, GU Xueping, ZHU Lingxin. Optimization of load restoration during network reconfiguring process of black-start restoration[J]. Power System Protection and Control, 2011, 39(17): 26-32.

[13] 冯欣桦, 黎洪光, 郑欣, 等. 计及不确定性的配电网合环点安全性与经济性评估[J]. 电力系统保护与控制, 2015, 43(10): 30-37.

FENG Xinhua, LI Hongguang, ZHENG Xin, et al. Security and economy evaluation of closed loop point of distribution network considering uncertainty[J]. Power System Protection and Control, 2015, 43(10): 30-37.

[14] 赵洪山, 赵航宇. 考虑元件故障率变化的配电网可靠性评估[J]. 电力系统保护与控制, 2015, 43(11): 56-62.

ZHAO Hongshan, ZHAO Hangyu. Distribution system reliability analysis considering the elements failure rate changes[J]. Power System Protection and Control, 2015, 43(10): 56-62.

[15] 何宇斌, 文云峰, 戴赛, 等. 基于故障风险指标排序的安全约束最优潮流[J]. 电力系统保护与控制, 2015, 43(13): 52-59.

HE Yubin, WEN Yunfeng, DAI Sai, et al. Security-constrained optimal power flow based on risk ranking of contingencies[J]. Power System Protection and Control, 2015, 43(13): 52-59.

[16] 宁光涛, 严超, 朱思睿, 等. 一种发电系统可靠性评估的混合加速算法[J]. 电网与清洁能源, 2014, 30(11): 41-45.

NING Guangtao, YAN Chao, ZHU Sirui, et al. A hybrid accelerated algorithm for generation system reliability evaluation based on sequential Monte Carlo Simulation[J]. Power System and Clean Energy, 2014, 30(11): 41-45.

[17] 梁海平, 顾雪平. 基于节点恢复可靠性的骨架网络重构[J]. 华北电力大学学报, 2014, 41(4): 11-16.

LIANG Haiping, GU Xueping. Skeleton-network reconfiguration based on node restoration reliability[J]. Journal of North Chin Electric Power University, 2014, 41(4): 11-16.

[18] 朱海南, 刘玉田. 考虑线路投入顺序的网架重构机组恢复多目标优化[J]. 电力系统自动化, 2014, 38(16): 53-58.

ZHU Hainan, LIU Yutian. Multi-objective optimization of unit restoration during network reconstruction consideringline restoration sequence[J]. Automation of Electric Power Systems, 2014, 38(16): 53-58.

[19] 刘艳, 刘国良, 顾雪平. 输电网架恢复方案线路投运风险评估[J]. 电力系统自动化, 2011, 35(13): 12-16.

LIU Yan, LIU Guoliang, GU Xueping. Line risk assessment in transmission network restoration scheme[J]. Automation of Electric Power Systems, 2011, 35(13): 12-16.

[20] 刘艳, 王涛, 王文炎. 用于网架重构方案运行风险评估的线路投运模型[J]. 中国电机工程学报, 2014, 34(7): 1124-1129.

LIU Yan, WANG Tao, WANG Wenyan. Model of restoring transmission lines for operational risk assessment of network-reconfiguration scheme[J]. Proceedings of the CSEE, 2014, 34(7): 1124-1129.

[21] MCCALLEY J, VITTAL V, ABI-SAMRA N. An overview of risk based security assessment[C] // IEEE Power Engineering Society 1999 Summer Meeting. Alberta (Canada): 1999: 173-178.

[22] 张毅明, 张忠会, 姚峰, 等. 基于风险理论的电力系统元件风险评估[J]. 电力系统保护与控制, 2013, 41(23): 73-78.

ZHANG Yiming, ZHANG Zhonghui, YAO Feng, et al. Risk assessment of power system components based on the risk theory[J]. Power System Protection and Control, 2013, 41(23): 73-78.

[23] 辛建波, 万军彪, 胡京, 等. 省级电网中短期风险评估系统及其不确定性建模方法研究[J]. 电力系统保护与控制, 2013, 41(1): 85-89.

XIN Jianbo, WAN Junbiao, HU Jing, et al. Research on the provincial power grid mid/short term risk assessment system and its uncertainty modeling approach[J]. Power System Protection and Control, 2013, 41(1): 85-89.

[24] 刘艳, 张凡, 顾雪平. 大停电后的机组投运风险评估[J]. 中国电机工程学报, 2013, 33(31): 106-113.

LIU Yan, ZHANG Fan, GU Xueping. Risk assessment for restoring units following large-scale blackout[J]. Proceedings of the CSEE, 2013, 33(31): 106-113.

[25] BILLINTIONR, WANG P. Distribution system reliability cost/worth analysis using analytical and sequential simulation technique[J]. IEEE Transactions on Power Systems, 1998, 13(4): 1245-1250.

[26] 高尚, 杨靖宇. 群智能算法及其应用[M]. 北京: 中国水利水电出版社, 2006: 89-91.

(编辑 魏小丽)

Optimization of unit’s restoration sequence based on minimizing of lines’ restoration risk corresponding to reconfiguration scheme

WANG Jiangyu, LIU Yan

(School of Electrical & Electronic Engineering, North China Electric Power University, Baoding 071000, China)

After a large-scale blackout, reasonable and orderly restoration is of great significance for minimizing the loss. The process of network reconfiguration is investigated specially from the point of switching in transmission lines. Taking lines’ operational reliability into consideration, a method of optimizing units’ restoration sequence is proposed. Firstly, a severity index in terms of the outage loss criteria is put forward to improve the definition of lines’ restoration risk corresponding to reconfiguration scheme. Secondly, a time-step frame of reconfiguration simulation accordant with the actual situation is established by means of interactive simulation between network reconstruction and units’ restoration. Furthermore, the model of optimizing units’ restoration sequence is constructed based on minimizing lines’ restoration risk corresponding to reconfiguration scheme and solved by the cross particle swarm optimization and Floyd algorithm. The outcome of its application on the New England 10-unit 39-bus power system indicates that units’ restoration sequences obtained fully consider possible spare paths for restoration as well as minimization of outage loss. Therefore, the method proposed can more effectively cope with the potential failure during switching in lines.

This work is supported by National Natural Science Foundation of China (No. 51277076).

large-scale blackout；network reconfiguration；lines’ restoration risk corresponding to reconfiguration scheme

10.7667/PSPC151202

2015-07-12；

2015-09-14

王江宇(1990-)，女，通信作者，硕士研究生，主要研究方向为电力系统安全防御与恢复控制；E-mail: 13780248076@163.com

刘 艳(1973-)，女，博士，教授，主要研究方向为电力系统安全防御与恢复控制，智能技术在电力系统中的应用。

国家自然科学基金项目(51277076)