一种考虑多次谐波的行波自然频率测距方法

李金泽，李宝才，翟学明



一种考虑多次谐波的行波自然频率测距方法

李金泽1，李宝才2，翟学明1

(1.华北电力大学控制与计算机工程学院，河北 保定 071003；2.保定学院信息技术系，河北 保定 071000)

在基于行波自然频率的输电线路单端故障定位方法中，主自然频率值的准确度是进行故障点精确定位的关键。目前的主自然频率的提取大多采用小波变换、MUSIC方法，小波分析受所选小波基影响较大，MUSIC的参数选择对频谱估计影响较大，它们都未能很好地解决这一问题。提出一种基于故障线路自然频率的单端测距新方法。该方法在提取主自然频率过程中首先对行波信号进行EEMD分解，并用ICA方法进行正交化处理，从而抑制WVD本身存在交叉项的问题，然后对各个分量进行WVD转换并叠加，获得正交的自然频率谱；进而综合考虑基波和多次谐波求取全局主自然频率。EMTDC仿真实验验证了该算法在不同故障类型、故障距离、过渡电阻和噪声情况下的可行性及其精度。

主自然频率的提取；全局主自然频率；集合经验模态WVD；输电

0 引言

高压输电线路是大容量、远距离送电的主要方式，因此，在发生故障时准确定位，快速排除故障对电力系统的安全运行具有重大意义。目前由于行波法[1]具有稳定性好、定位精度高等优点而备受广大电力工作者的青睐。行波法又分为单端法和双端法[2]。单端法[3]虽然仅需要依赖一端采集的故障信号就可以计算故障距离，但是传统单端法的准确性主要在识别反射行波的波头方面，而且精确度一直都得不到保证。双端法[4]虽然避免了这一难题，但是必须要保证双端的检测设备同步，对硬件要求较高，成本也随之骤增。因此，一些研究人员为了克服以上面临的问题，对故障行波频谱大量的分析研究，提出了基于自然频率的线路故障定位方法。

在文献[5-6]中提出输电线路发生故障时，故障电流中的某种频率成分与故障距离存在着一定的比例关系，通过对该频率的提取实现单端定位。准确地提取主自然频率值是基于行波的故障定位方法的基础。文献[7]为了更准确地提取主自然频率值，同时从时域和频率特征出发考虑。文献[8]考虑到母线段阻抗不连续会导致在折反射过程中降低主自然频率值，引入修正系数来修正提取到的主自然频率值。上述这些方法在大部分情况中能取得较好的主自然频率值。但仍存在问题：在确定主自然频率值时仅依靠提取单一的主自然频率峰值，而该值受噪声、线路不连续阻抗、谐波干扰以及线路耦合等因素的影响很大，固提取到的主自然频率值并不能得到保证，从而影响定位效果。

同时人们提取主自然频率常用的方法主要有傅立叶变换、小波变换(Wavelet Transform，WT)[9]和多信号分类算法(Multiple Signal Classification，MUSIC)[10]。傅立叶变换在处理随即非平稳信号时效果不佳，误差较大；虽然在理论上WT和MUSIC的频率分辨率是自适应的，但由于它们所提取的频率为统计频率(伪频谱)，故不能得到信号的真实频谱；同时，MUSIC是一种基于参数的频谱估计方法，参数的选择对处理结果影响较大，因此在实际应用中存在一定难度。

综合考虑以上存在的问题，本文提出一种基于故障线路自然频率的单端测距新方法。在提取主自然频率过程中使用了一种集合模态分解和ICA(Independent Component Analysis，ICA)相结合的WVD(Wiger-Ville Distribution)新方法，获得正交的主自然频率频谱；进而综合考虑基波和多次谐波求取全局主自然频率，通过推导其为主自然频率和多次自然频率成分倒数的加权平均数。利用该全局主自然频率值，更加精确地定位。

1 考虑多次谐波的自然频率测距方法原理

1.1 故障行波的全局主自然频率

当线路发生故障时，形成的故障暂态行波在线路两端和故障点之间来回反射，其在频域上表现为以为基频的无穷多次谐波之和，在频谱分布中的峰值为行波的固有频率[8]。其中第一个峰值为自然频率主成分，其含能量最高、幅值最大而频率值最低。频率值为主自然频率值整数倍的称为多次自然频率成分。

双电源输电线路模型如图1所示，其中输电线路总长度为，两端阻抗分别为和。假设故障发生在距离1端处。

根据文献[7]中的理论，线路极小感抗时，母线1端故障距离与自然频率主成分的关系为

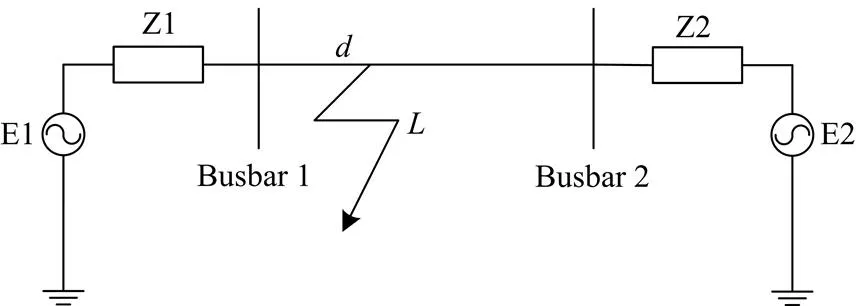
图1双电源供电模型

由式(1)可构造方程组如式(3)。

其中反射角是由线路两端阻抗决定，当输电线路确定时，1端反射角可近似相等，因此。同时文献[11]表明，当行波频率较高时，波速受频率的影响较小，可近似认为不变，而自然频率一般都在几百赫兹以上，因此可以认为波速相等，即，通过各次谐波得到的故障距离理论上也为一个定值。

将式(3)中各式相加化简得：

将式(4)、式(5)联立，化简可得：

由式(6)可知，全局主自然频率为多次谐波主自然频率倒数的加权平均值。截止频率的选取需要进一步确定。

1.2 考虑多次谐波的自然频率测距方法流程

步骤一：获取输电线路发生故障时线路两端的三相电流数据，采用clarke和凯伦鲍尔方法进行解耦，根据故障类型选取相应的模量作为研究对象。

步骤二：首先对选取模量进行EEMD分解。并用ICA方法进行正交化处理，然后对各个分量进行WVD转换并叠加，获得正交的自然频率谱。

步骤三：利用式(7)在频谱中选取个峰值，即幅值最高且频率最低。读出、、、。

步骤三：根据输电线路参数，利用上一节的式(2)计算反射角，使用实验得出的、、、，通过式(6)分别求出1端全局主自然频率。

2 考虑多次谐波的自然频率测距方法的实现

2.1 相模变换

行波在实际输电系统传播过程中存在色散现象，导致行波以不同模分量的形式传播，每种模分量中各频率成分的传播速度和衰减都不相同，而且会出现“模混杂”的现象，对测距结果有较大影响。因此，根据故障类型选取合适的模量，将一定程度上提高测距精度。

1) 在系统对称的条件下，发生三相短路/接地故障和两相短路/接地故障时，将系统故障电流完全解耦后，选取模作为分析对象。

2.2 故障行波自然频率的提取

在本文中，从主自然频率本身的特点出发，在现有的时频分析方法中选取Wigner-Ville分布(Wigner-Ville Distribution，WVD)。WVD具有高的时频分辨率、能量集中性及满足频率边缘等特性，能够清晰准确地提取主自然频率值。但是该方法本身存在交叉项干扰问题[12]，严重影响了WVD的应用。为了抑制交叉项，可首先利用集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法将行波信号分解成多个固有模态分量，并利用ICA技术使EEMD分解的分量具有正交性，根据WVD定义，正交分量之间交叉项为零，即正交分量之和的WVD可以用正交分量的WVD之和来表示，从而达到抑制交叉项的目的。

1) EEMD是针对非平稳信号的一种自适应的、高效的数据分解方法[13]，针对EMD出现的模态混叠和虚假分量的问题，将白噪声加入到所需分解的信号中补充一些缺失的尺度，达到更好的分解结果。利用EEMD方法对信号进行分解，得到有限个基分模式分量

从大量实验中可知[14]，在分解出的分量中存在部分伪分量，可利用相关系数剔除伪分量，求出与原信号的相关系数，其值越大相关性越大，反之则越小。将阀值设置为相关系数序列中最大值的1/10，剔除小于阀值的无关分量。相关系数计算方法为[15]

2) 虽然利用EEMD方法可以分解出一系列单模态函数，但是无法保证全局正交，并且分量之间会含有相同频率成分。为了解决这一问题，本文采用独立分量分析(ICA)技术，使分离后的信号分量之间彼此独立。

ICA是一种盲信号分离技术[16]，它是一种依赖于统计测量的混合信号分离方法，可以有效地解决EEMD过程中模态混叠效应导致的分量无法分离问题，获取全局正交分量。

图2为一个额定电压500 kV，500 km的输电线路在300 km处发生三相接地故障的电流波形。故障发生在0.2 s，持续时间0.1 s。对以上故障电流信号进行相模变换后[17]，选取的模量，经过EEMD分解和ICA转换的各分量如图3所示，、、、为原信号分解后的真实成分且相互独立。

图4、图5为2.1节采用WVD方法在消除交叉项前后得到的灰度分布图，图中横坐标为采样点序列，纵坐标为归一化频率，图像的颜色变换表示能量的高低，由两图对比明显看出，图5中间原本存在的交叉项消除，验证了该抑制交叉项问题的可行性。

2.3 过渡电阻对主自然频率值的影响

当输电线路故障点存在过渡电阻时，由文献[18]可知，暂态行波在线路中来回反射的过程中，由于过渡电阻的存在，行波能量衰减较大，但对频谱中各分量频率值影响不大，仅是在幅值上的改变。

在本文算法中幅值的改变将会影响截止频率的选取，对其讨论如下：

3 仿真与分析

3.1 实例仿真

在PSCAD平台上建立图1所示500 kV输电线路仿真模型[19]。线路长500 km，其中电源1:500∠50 kV，495∠30 kV，土壤电阻率=100，线路参数，，，，，，两端对地电容为0.01 μF。采样频率100 kHz，故障发生在距离Busbar 1端母线300 km处。

以三相相间/接地短路故障为例，过渡电阻为30W，经过相模变换选取模量作为分析对象，使用本文主自然频率提取算法得到Busbar 1端故障电流频谱如图6所示。

图6 Busbar 1端电流频谱

3.2 适应性分析及比较

3.2.1不同的故障类型

在故障距离为300 km处的线路上进行不同故障类型的仿真实验。其中过渡电阻为30W，算法改进前后分别计算故障距离，其测距结果及误差如表2所示。

实验结果表明，改进后的故障定位算法在精确度上有明显提高；且通过比较，单相故障时故障结果相对误差较大，其主要原因在于，单相故障在经 过相模变换后得到的模量中往往掺入了部分0模量；总体而言，改进后的算法对不同类型故障具有良好适应性。

表1 改进前后的测距结果

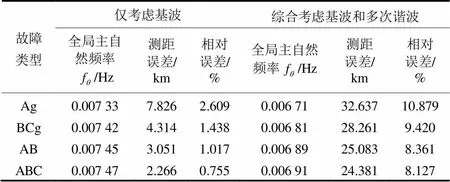
表2 算法改进前后在不同故障类型时的测距结果

3.2.2不同的故障距离

输电线路在不同位置发生三相相间/接地短路故障时，算法改进前后的误差比较如图7所示。通过比较可知，综合考虑基波和多次谐波所计算的定位结果要比仅考虑基波得到的结果更精确。

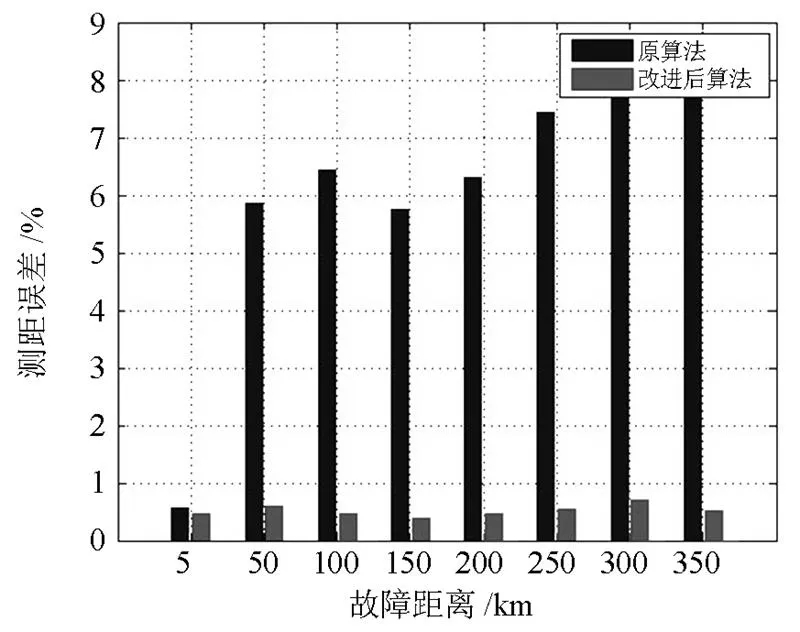
图7 不同故障距离的测距误差

3.2.3不同的过渡电阻

在故障距离为300 km处的线路上设置三相相间/接地短路故障，不同过渡电阻时算法改进前后的测距结果和误差如表3所示。总结表中结果可知，综合考虑基波和多次谐波所得到的测距结果，随着过渡电阻的增加，定位效果并没有明显变差，基本符合2.3节中推导的结论；而原算法中仅考虑基波的测距结果随着过渡电阻增加误差明显增加。证实改进算法在过渡电阻因素中有明显优越性。

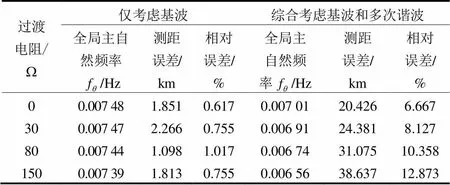
表3 不同过渡电阻下的测距结果

3.2.4不同噪声环境下

在信号中加入不同信噪比的白噪声后，改进后的算法定位误差随故障距离的变化如图8所示。其中过渡电阻为30W。

由图8可知，改进后的算法在不同噪声环境下表现的相对稳定，其原因在于主自然频率提取方法采用了集合经验模态WVD算法，其在提取中首先将含有噪声的信号进行EMD分解，即分解成为一系列具有不同特征时间尺度的固有模态函数的和，然后将每个分量取平均，由于平均分布的噪声一般具有零均值特性，取平均就可以使噪声基本消失，起到降噪的效果。实验结果表明该测距方法在不同噪声环境下具有一定的适应性。

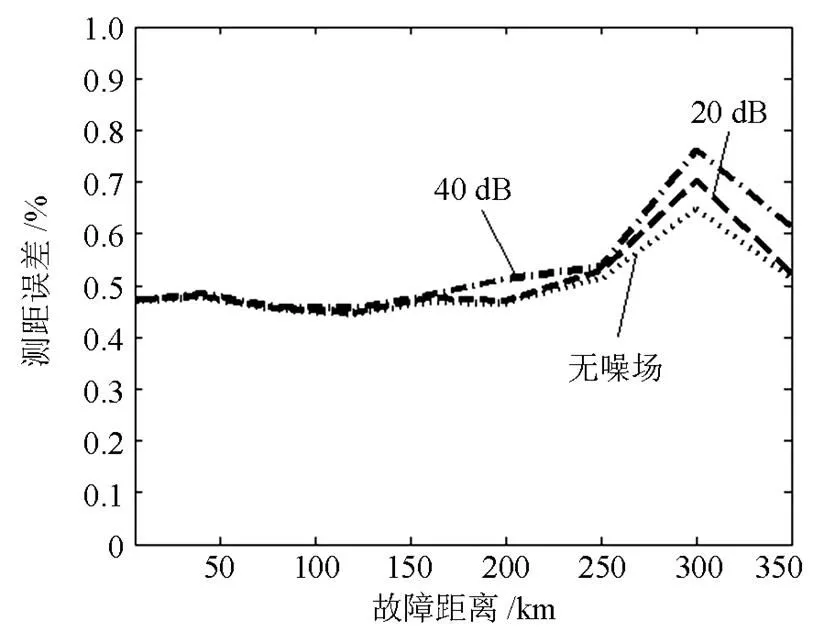
图8 不同噪声水平时的测距结果

4 结论

在基于主自然频率的定位方法中，本文从主自然频率的确定原理和提取方法两个方面做了改进，得到更为准确的主自然频率值，从而提高了测距精度。仿真结果表明，本文算法受不同故障、不同距离、不同过渡电阻影响较小，对不同信噪比的噪声有较强适应性，误差在可接受范围内。

[1] 牛睿, 梁军, 张峰, 等. 基于可变行波辨识时窗的单端故障定位方法[J]. 电力系统保护与控制, 2014, 42(24): 56-64.

NIU Rui, LIANG Jun, ZHANG Feng, et al. Single-ended fault location method based on variable time windows for traveling wave identification[J]. Power System Protection and Control, 2014, 42(24): 56-64.

[2] 覃剑, 葛维春, 邱金辉, 等. 输电线路单端行波测距法和双端行波测距法的对比[J]. 电力系统自动化, 2006, 30(6): 92-95.

QIN Jian, GE Weichun, QIU Jinhui, et al. Study on single terminal method and double terminal method of traveling wave fault location in transmission line[J]. Automation of Electric Power Systems, 2006, 30(6): 92-95.

[3] 郑秀玉, 丁坚勇, 黄娜. 输电线路单端故障定位的阻抗-行波组合算法[J]. 电力系统保护与控制, 2010, 38(6): 18-21.

ZHENG Xiuyu, DING Jianyong, HUANG Na. Impedance-traveling wave assembled algorithm of one-terminal fault location for transmission lines[J]. Power System Protection and Control, 2010, 38(6): 18-21.

[4] 李勋, 黄荣辉, 姚森敬, 等. 一种改进行波时频复合分析的杆塔故障定位方法[J]. 电力系统保护与控制, 2015, 43(20): 130-136.

LI Xun, HUANG Ronghui, YAO Senjing, et al. A novel fault location method by tower based on traveling wave time-frequency analysis[J]. Power System Protection and Control, 2015, 43(20): 130-136.

[5] SWIFT G W. The spectra of fault-induced transients[J]. IEEE Transactions on Power Apparatus and Systems, 1979, 98(3): 940-947.

[6] 邬林勇, 何正友, 钱清泉. 单端行波故障测距的频域方法[J]. 中国电机工程学报, 2008, 28(25): 99-104.

WU Linyong, HE Zhengyou, QIAN Qingquan. A frequency domain approach to single-ended traveling wave fault location[J]. Proceedings of the CSEE, 2008, 28(25): 99-104.

[7] 林圣, 武骁, 何正友, 等. 基于行波固有频率的电网故障定位方法[J]. 电网技术, 2013, 37(1): 270-275.

LIN Sheng, WU Xiao, HE Zhengyou, et al. A power system fault location method based on natural frequency of travelling waves[J]. Power System Technology, 2013, 37(1): 270-275.

[8] 徐高, 龚庆武, 李勋, 等. 一种利用行波自然频率的杆塔故障定位新方法[J]. 电力系统自动化, 2014, 28(5): 78-82.

XU Gao, GONG Qingwu, LI Xun, et al. A novel method of tower fault location using natural frequencies of travelling wave[J]. Automation of Electric Power Systems, 2014, 28(5): 78-82.

[9] 尚海昆, 苑津莎, 王瑜, 等. 基于交叉小波变换和相关系数矩阵的局部放电特征提取[J]. 电工技术学报, 2014, 29(4): 274-281.

SHANG Haikun, YUAN Jinsha, WANG Yu, et al. Feature extraction for partial discharge based on cross-wavelettransform and correlation coefficient matrix[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 274-281.

[10] 武骁, 何正友, 彭少博, 等. 基于行波固有频率的特高压直流输电线路纵联保护方法[J]. 电力系统保护与控制, 2013, 41(11): 67-73.

WU Xiao, HE Zhengyou, PENG Shaobo, et al. A UHVDC transmission line pilot protection method based on natural frequencies of traveling wave[J]. Power System Protection and Control, 2013, 41(11): 67-73.

[11] LIN S, HE Z Y, LI X P. Travelling wave time-frequency characteristic-based fault location method for transmission lines[J]. The Institution of Engineering and Technology, 2012, 6(8): 764-772.

[12] 邹红星, 戴琼海, 李衍达, 等. 不含交叉项且具有WVD聚集性的时频分布之不存在性[J]. 中国科学: E辑, 2001, 31(4): 348-354.

[13] 朱宁辉, 白晓民, 董伟杰. 基于EEMD的谐波检测方法[J]. 中国电机工程学报, 2013, 33(7): 92-98, 14.

ZHU Ninghui, BAI Xiaomin, DONG Weijie. Harmonic detection method based on EEMD[J]. Proceedings of the CSEE, 2013, 33(7): 92-98, 14.

[14] 宋亚奇, 周国亮, 朱永利, 等. 云平台下并行总体经验模态分解局部放电信号去噪方法[J]. 电工技术学报, 2015, 30(18): 213-222.

SONG Yaqi, ZHOU Guoliang, ZHU Yongli, et al. Research on parallel ensemble empirical mode decomposition denoising method for partial discharge signals based on cloud platform[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 213-222.

[15] 张佩, 赵书涛, 申路, 等. 基于改进EEMD的高压断路器振声联合故障诊断方法[J]. 电力系统保护与控制, 2014, 42(8): 77-81.

ZHANG Pei, ZHAO Shutao, SHEN Lu, et al. Research on vibration and acoustic joint mechanical fault diagnosis method of high voltage circuit breaker based on improved EEMD[J]. Power System Protection and Control, 2014, 42(8): 77-81.

[16] 赵阳, 夏欢, 邱晓晖, 等. 基于独立分量分析算法的医疗电子设备辐射电磁干扰EMI噪声分析方法[J]. 电工技术学报, 2015, 30(17): 180-190.

ZHAO Yang, XIA Huan, QIU Xiaohui, et al. The radiated EMI analysis method for electromedical equipments based on ICA[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 180-190.

[17] 刘琦, 邰能灵, 范春菊, 等. 同塔四回不对称参数线路的相模变换[J]. 电工技术学报, 2015, 30(18): 171-180.

LIU Qi, TAI Nengling, FAN Chunju, et al. Phase-mode transformation of asymmetry-parameter four-parallel lineson the same tower[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 171-180.

[18] 廖凯, 何正友, 李小鹏. 基于行波固有频率的高压直流输电线路故障定位[J]. 电力系统自动化, 2013, 37(3): 104-109.

LIAO Kai, HE Zhengyou, LI Xiaopeng. Fault location of HVDC transmission line based on the natural frequency of travelling waves[J]. Proceedings of the CSEE, 2013, 37(3): 104-109.

[19] 姚致清, 张茜, 刘喜梅. 基于PSCAD/EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制, 2010, 38(17): 76-81.

YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J]. Power System Protection and Control, 2010, 38(17): 76-81.

(编辑 葛艳娜)

Single terminal fault location by natural frequencies of travelling wave considering multiple harmonics

LI Jinze1, LI Baocai2, ZHAI Xueming1

(1. School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, China; 2.Information Technology Department, Baoding University, Baoding 071000, China)

In the single terminal fault locating method of transmission line based on traveling wave natural frequency, the accuracy of extracting primary natural frequency is the key to caring out to pinpoint trouble spots in. Currently, wavelet transform and MUSIC method are commonly used for extracting primary natural frequency. Wavelet analysis is influenced by the selected wavelets and the parameters’ selection greatly impacts spectral estimation in MUSIC, which can’t solve this problem well. A new single ended fault location method of extracting faulted line natural frequencies is described. The traveling wave signal is decomposed by EEMD and orthogonal process is made with ICA method to suppress the WVD's problem of cross-term, and then each component of WVD is converted and superimposed to obtain the natural frequency spectrum orthogonal. Then the global primary natural frequency is obtained considering the fundamental and harmonics. Simulation experiment by EMTDC confirms the feasibility and accuracy of the proposed algorithm under different fault types, fault distance, transition resistance and noise situation.

This work is supported by National Natural Science Foundation of China (No. 60974125).

accuracy of extracting primary natural frequency; global primary natural frequency; ensemble empirical mode WVD algorithm; noise; transmission line

10.7667/PSPC151521

2015-08-27；

2016-01-13

李金泽(1991-)，男，硕士研究生，从事电力系统及在线监测技术的研究；E-mail: li_jinzel123@163.com

李宝才(1983-)，男，硕士，助教，从事计算机软件方向的研究;

翟学明(1967-)，男，博士，副教授，从事电力系统自动化方向的研究。

国家自然科学基金项目(60974125)