一种基于实测数据的谐波源定位方法

王 岭，陈红坤，王志成，徐 坤



一种基于实测数据的谐波源定位方法

王 岭，陈红坤，王志成，徐 坤

(武汉大学电气工程学院，湖北 武汉 430072)

为了准确划分各谐波源责任以便采用技术及经济手段治理谐波问题，提出了一种基于实测数据的谐波源定位方法。该方法以系统母线的谐波电压幅值及相位作为量测量，考虑一定的建模及测量误差，根据系统各节点的谐波功率与母线阻抗之间的符号关系对可疑母线进行分类。提出定位指标对各节点进行排序，确定最为可能的谐波源位置，减少后期不必要的勘测工作。最后，在ETAP 12.6中建立了IEEE 14节点的算例模型并进行计算验证，计算结果证明了提出方法的有效性。

量测配置优化；离散二进制粒子群；谐波功率；谐波源定位；定位指标

0 引言

随着配电网对新能源的接纳能力不断增强，电力电子装置与非线性用电设备在国民生产各部门应用越来越广泛，而由其引起的电力系统谐波污染也日益严重[1-5]。由于谐波往往不是孤立存在于电网的；各母线电压畸变也是由于电网中所有非线性设备共同作用的结果[6-7]。文献[1]首次利用了谐波状态估计来识别谐波源，并总结了判定谐波源存在的判据及影响估计误差的4个因素。文献[2]利用关联矩阵的概念建立起谐波量测量与状态变量的数学模型，提出了电力系统连续谐波的状态估计算法，为了减少未知状态变量的数目，将节点分为非谐波源和可疑谐波源两类。文献[3]从量测量和状态变量两方面改进了谐波状态估计在谐波源定位中的应用。文献[8]针对谐波源随机分布及非谐波源节点存在干扰电流的状况，提出基于改进稀疏表示法的谐波源定位。

在目前的谐波源定位方法的研究工作中，一般选取节点的谐波电压作为量测量[9-10]，以节点的谐波注入电流作为状态变量来判断负荷是否为谐波源，而在配电网含有多谐波源的背景下，仅以谐波电流作为判断依据无法反映谐波源之间的相互影响，造成定位不准确[11-14]。在选择量测数据点时，以往的研究通常需要估计谐波源嫌疑区域，然后进行定位。如果预估出现偏差，则可能造成重复工作或是定位偏差。

本文提出一种基于实测数据的谐波源定位方法。将系统节点的谐波电压作为量测点，考虑一定的建模与测量误差，将量测量与系统阻抗矩阵作为输入，分析各母线注入谐波功率与母线阻抗的符号关系，分类可疑母线。计算各母线的定位指标值，并对其排序，从而确定最为可能的谐波源位置。其中，分布式电源作为重要的谐波污染源。最后，在ETAP 12.6中建立了一个14节点的配电网模型，仿真验证了本文所以方法的有效性。

1 谐波源定位原理

电力系统及非线性负荷的建模是谐波源定位的基础。在本文中，谐波源定位的讨论均基于以下假设：

1) 根据电网的电源、负荷及线路参数，系统是平衡的。因此，任何相位关系均是已知的。

2) 输电线路模型等效为RL串联电路，忽略其对地电容。不同谐波频率下输电线路的电抗值均有较高的精确度。

3) 负荷模型为RL串联模型。

4) 谐波电压幅值及相位量测装置对所有母线均适用。

5) 网络中若有分布式电源接入，其注入的谐波电流是可知的。非线性负荷被等效为一个恒定电流源。显然，母线上的谐波电压为各个谐波源在该母线上产生的谐波电压之和。

假设条母线配电网系统的非线性电源数目为，那么母线上的谐波电压可以由如下公式计算得出：

大多数非线性电源中的电力电子器件为6或12脉冲的变换器，其产生的偶次谐波较少，特征谐波一般为和，其中为奇数。并且若网络中变压器的连接方式为，3次谐波可被忽略。因此，确定主要电源的5次、7次、11次、13次谐波已经足够确定系统中谐波源的位置。

假设系统中仅有一处谐波源连接在母线上，其向系统注入的次谐波视在功率为

利用式(1)和式(2)可以得出谐波视在功率的如下形式：

将上述谐波视在功率写成实部与虚部形式，即谐波有功功率与无功功率为

当系统中存在多个谐波源，母线上的谐波电压由式(1)可得。在系统存在其他电源时，无论母线上是否有非线性负荷，其注入的谐波有功功率均可能出现负的情况，因此，注入的谐波有功功率为正是该母线上有非线性负荷的充分而非必要条件。但即使母线上无非线性电源，其谐波有功功率注入仍可能为负。同样的，谐波无功功率也可能会出现符号逆转的情况，而无源负荷注入的谐波无功功率则与其是容性负荷还是感性负荷有关。

式中：为与母线相连的支路合集；为母线与母线之间的支路导纳。

计算得出谐波电流后，谐波视在功率即可通过式(2)计算得出。最后，根据，，，四项指标的符号，可以反映该母线存在谐波源的可能性。

2 母线谐波电压的获取

2.1 量测装置配置

根据上一节的分析，本文提出的谐波源定位方法是将谐波电压幅值及相位作为量测量。若将系统所有节点均配置谐波量测装置，必然会造成大量的数据冗余，并且随着母线数的增加，成本会显著增加。因此，确定所需量测装置的最小数量以及合适的测量节点就变得十分重要。在配网下，若某一母线的电压被直接测量或是由其他母线的测量电压计算得到，我们称该母线是可观测的，若系统的所有母线电压可观测，我们则认为系统是完全可观测的。

量测装置配置的优化可分为以下两个步骤：

a) 根据各个母线与系统的连通性，利用母线的连通性指标与进化指标来确定最佳安置节点的数量。然后，将选定的母线作为量测装置安装节点的部分最优解。这一步称作指标法，该方法可以显著减少下一步的工作量。

b) 采取BPSO算法确定量测装置的其他最优安装节点。

由于量测装置安装在某一母线可以使得与之相关的母线均可观测，所有这类母线均可由二进制连通性矩阵来确定：

指标法首先要筛选出系统的末端母线，显然，末端母线仅与一条母线相连。若量测装置安装在末端母线，其观测的母线不可能超过两条。因此，为了监测末端母线电压，我们可将量测装置安装在与末端母线相连的母线上，此时系统便可能会出现唯一一条有着最大连通性指标值的母线。

母线的连通性指标是指在该母线上安装量测装置后，将不可观测的母线变为可观测母线的数量。例如第条母线，其连通性指标值为矩阵第行所有元素之和减去1。如果出现多条母线的连通性指标值同时最大，则需要选出进化指标值最大的母线。母线的进化指标指的是保持原有量测装置不变，另增加一个量测装置在该母线上，矩阵的所有元素之和。进化指标值高意味着该母线与系统的连通性小，这也是本文优先选择联系少的不可观测母线的原因。

指标法的结束条件有两个：

2) 缺少唯一的拥有最大连通性指标值或同时拥有最大的连通性指标值和进化指标值的节点，这意味着经过指标法分配后仍有部分节点不可观测。我们需要利用BPSO算法得到完整的最优解。

两个条件不可能同时满足，因此只有在条件2的情况下才需要使用BPSO算法，应用指标法的流程图如图1所示。

图1指标法的应用流程图

2.2量测配置优化的BPSO算法

本文将量测装置的节点分配问题视为一个优化问题，其目标函数是量测装置数量的最小化和测量冗余度的最大化，其约束条件是使系统完全可观测。

设二进制向量的定义如下：

则BPSO问题可定义如下：

其中，为系统母线数为的二进制连通性矩阵，是的单位向量。表示的是量测装置的全部数量，为实际测量冗余度函数。为理想测量冗余度向量，其所有元素均等于理想测量冗余度加1。和分别为与的权重。

显然，上述的不等式约束条件为系统完全可观测。考虑该不等式约束条件，我们可以定义BPSO的适应度函数如下：

其中，为一个非常大的常数。

在整个BPSO流程中，预先设定的初始节点相关的中的元素设为1，可以提高其收敛性以及减少其达到全局最优解需要的迭代次数。

3 谐波源定位及谐波注入水平估计

通过上一节的分析，我们可将母线存在谐波源的可能性分为A，B，C，D四类，如表1所示。分类母线的流程如图2所示。

表1各类母线的谐波源存在可能性

Table 1 Possibility of existing harmonic sources on all kinds buses

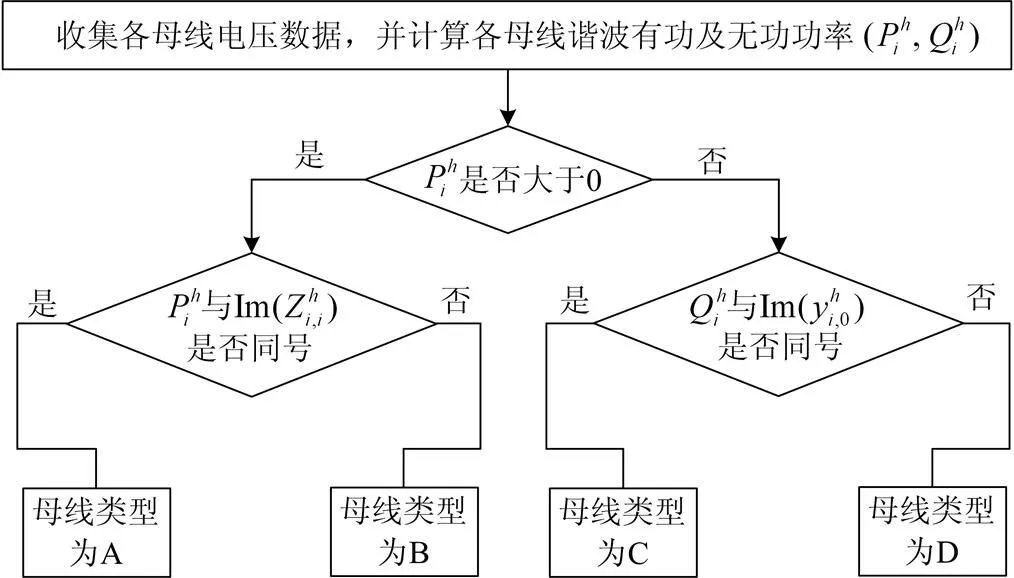
图2母线分类流程图

显然，在理想情况下，含有谐波源的母线应该属于A类。然而，由于谐波电压的测量误差，形成阻抗矩阵时产生的误差和系统中有其他一个或多个电源的原因，可能会出现一条非线性母线被分类到B, C, D类中。

完成母线分类之后，我们需要对可能的非线性母线进行现场勘测，得到准确的谐波注入水平，本文引入了定位指标()，以得到对母线进行现场勘测的优先级。

第条母线的定位指标值为

将以上算法应用于7次谐波分析，由于各次谐波相互不受影响，也可将其类推到其他频率的谐波分析上。7次谐波电压可由式(1)计算得出，但实际中，由于负荷建模的误差，我们很难得到准确的阻抗矩阵。本文将该误差反映到阻抗矩阵中，考虑内的随机电阻误差，内的电抗误差。经过以下步骤进行仿真分析。

1) 将负荷等效为RL串联模型，在7次谐波频率下计算各个负荷的阻抗大小；

2) 计算各支路的电抗以及各支路的对地电容；

3) 考虑阻抗误差，利用阻抗矩阵形成算法得到系统的阻抗矩阵；

4) 利用前面章节讨论的方法计算系统各个母线的谐波电压；

5) 利用式(6)计算各个母线总的7次谐波电流注入；

6) 利用式(4)计算各个母线的7次谐波有功功率注入；

7) 利用式(5)计算各个母线的7次谐波无功功率注入；

8) 根据图2对各个母线进行分类，并利用式(8)计算各个母线的定位指标值。

4 算例分析

利用IEEE 14节点系统验证本文提出的方法的有效性，由于国内配电网几乎都为开环运行，因此去掉原来14节点的部分支路，如图3所示。本算例包含了3个谐波源和1个分布式电源，节点5与外部电网相连，系统的基准功率为100 MVA，基准电压为10 kV。各电源的谐波电流注入为如表2所示。

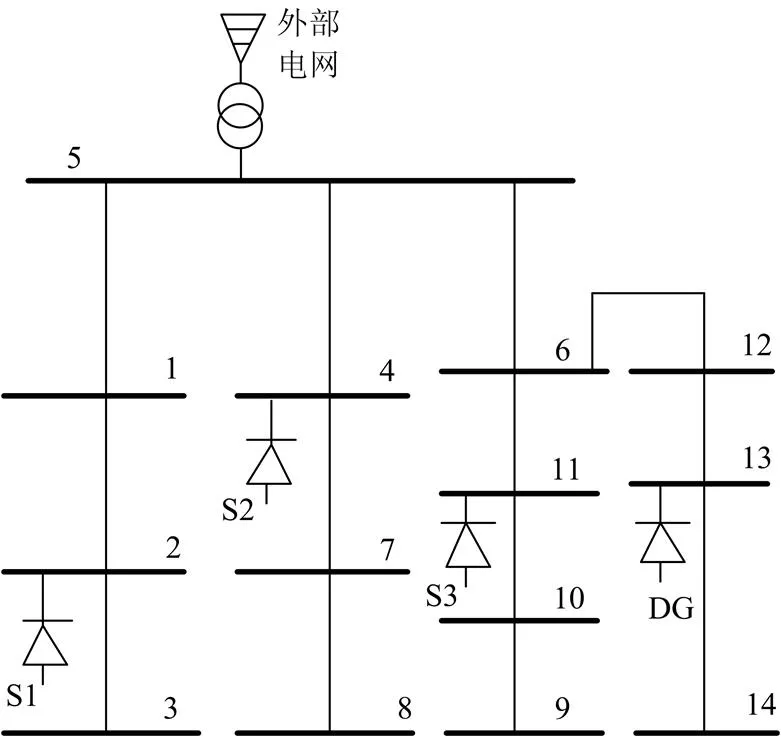
图3去掉部分支路的IEEE 14节点图

表2各电源的7次谐波电流注入值

Table 2 Seventh harmonic current injection of each sources

4.1谐波量测装置配置优化

确定谐波量测装置的安装位置使得系统完全可观测，并使得数据冗余度最少，成本最低。系统的连通性矩阵如下：

在确定了系统的连通性矩阵后，谐波量测装置的最优安装位置利用指标法以及BPSO算法得到，如表3所示。对比于文献[15]，该文献根据系统拓扑结构安装量测装置而使系统完全可观测，在其给出的37节点系统的算例中，得出的结论为需要安装谐波量测装置的数目为25，若利用本文提出的方法则只需安装12处。

表3 确定量测装置的全局最优解

4.2 谐波源位置的确定

本文将分为两种情况来确定谐波源位置，第一种情况考虑负荷建模误差而忽略测量误差；第二种情况对两种误差均进行考虑。本算例中，除了第13、14条母线，的符号均为负。而的符号为正的母线标号为5, 6, 8, 12, 14，为负的母线标号为1, 2, 3, 4, 7, 9, 10, 11, 13。

情况一：假设所有量测装置的测量值足够准确，仅存在负荷建模误差，应用本文提出的方法对系统母线分类(表4)，计算反映各母线上的谐波源容量大小的定位指标，即母线的勘测优先级，如表5所示。

根据表5给出的结果，我们可以得出以下几点结论：1) 仅仅考虑负荷建模误差，所有非线性母线的谐波有功功率注入均为正，因此它们一定属于A类或者B类。而B类的出现主要是由于其他谐波电源的影响。2) 所有线性母线均属于D类，因此对线性与非线性母线的区分十分直观。3) 定位指标清晰地反映各母线的谐波电流注入水平，因此该方法可完成预期的目标，即确定谐波源所处母线以及估计该谐波源的谐波电流注入水平。4) 由于负荷建模的误差，线性母线的干扰性指标值是一个十分接近于0的值，但不是0。

表4各母线的分类结果(情况一)

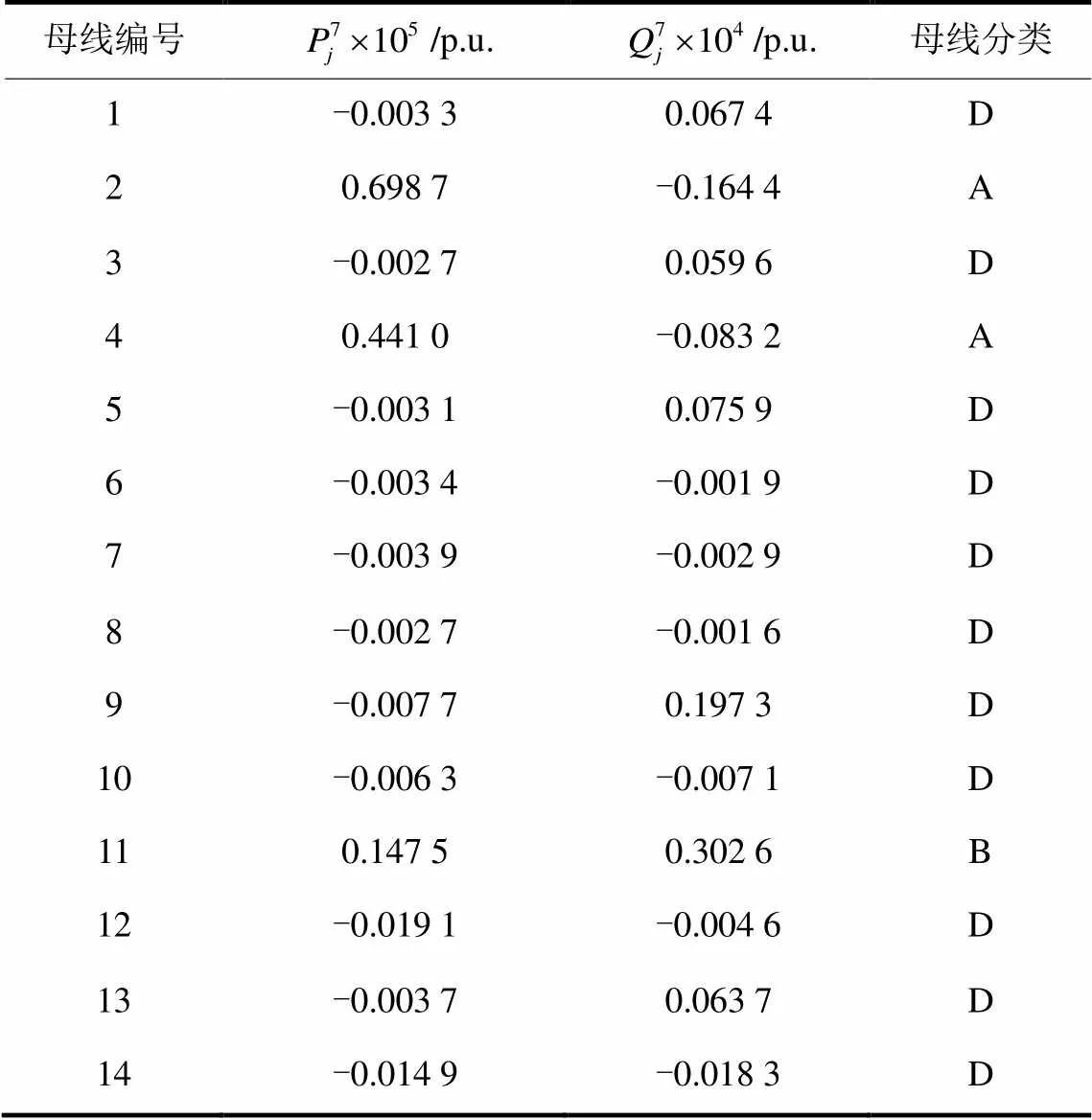
Table 4 Classification results of the buses (case 1)

表5各母线的勘测优先级排序(情况一)

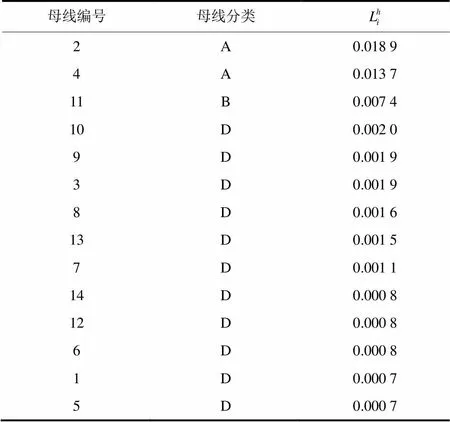
Table 5 Survey priority ranking of the buses (case 1)

情况二：考虑建模误差以及测量误差，在本文中我们引入0.5%以内的随机谐波电压幅值误差以及0.28°以内的随机谐波电压相角误差[16]来进行仿真分析。显然在该情况下，由于测量误差的随机性，结果并不唯一，但根据表6、表7我们仍可以得出几点结论：1) 由于两种误差的存在，一些线性母线可能会被认为成B类，此时，母线分类已经不足以用来确定谐波源的位置，需要结合干扰性程度指标来共同判定。2) 存在非线性负荷的母线的干扰性程度指标值仍比其他母线高，即使其他部分母线也被分类为B类。因此，定位指标仍可以用来估计谐波源的渗透率大小。3) 本文对于规模较小的谐波源定位十分困难，由于两种误差的存在，可能会被分类到四类母线中的任意一类，几乎不能够根据表中的数据来确定谐波源位置。4) 一些线性母线的干扰性指标值与0仍有较大距离，若这些母线的谐波有功功率注入为正，则会被分类为A类或B类母线，且会被怀疑成非线性母线，引起后期不必要的现场勘测需求。

表6各母线的分类结果(情况二)

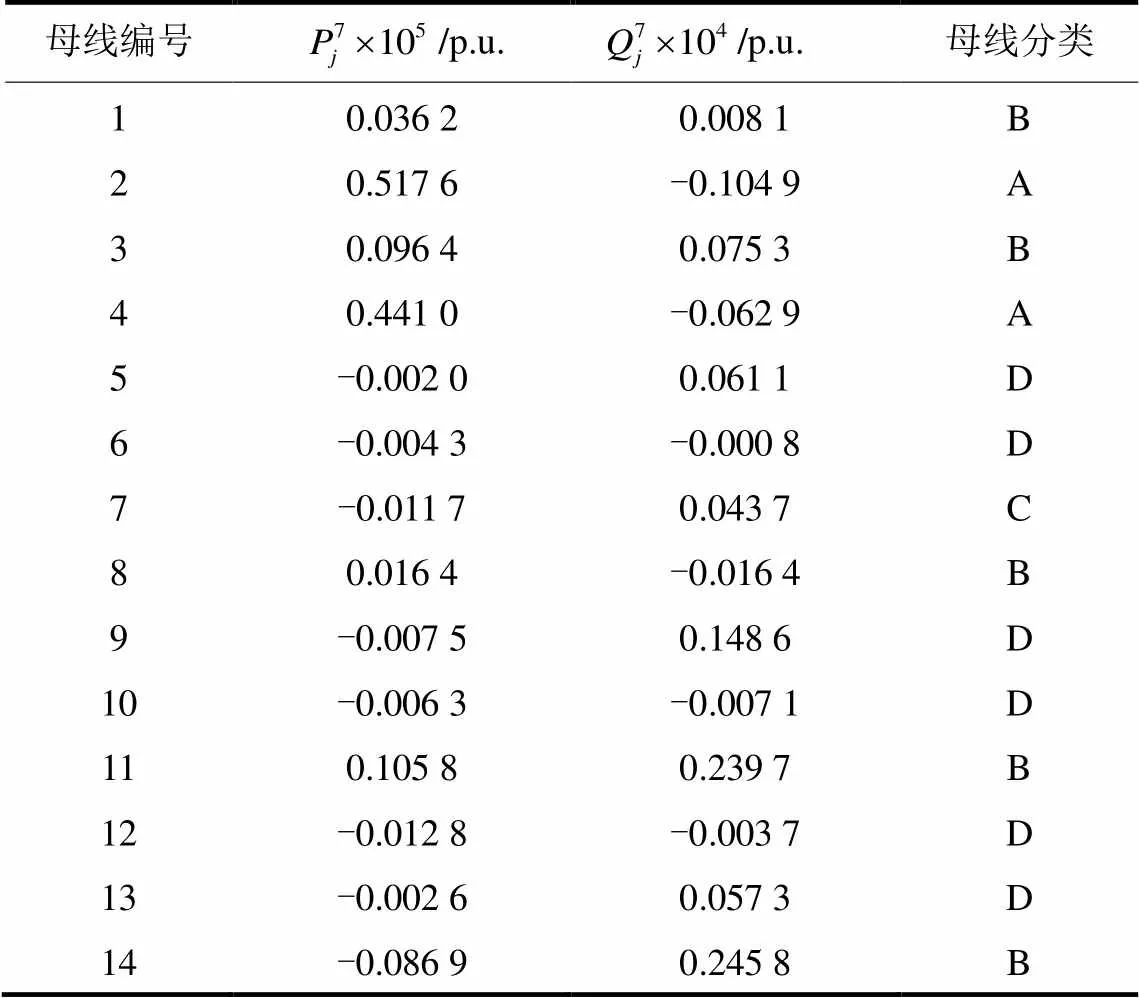
Table 6 Classification results of the buses (case 2)

表7各母线的勘测优先级排序(情况二)

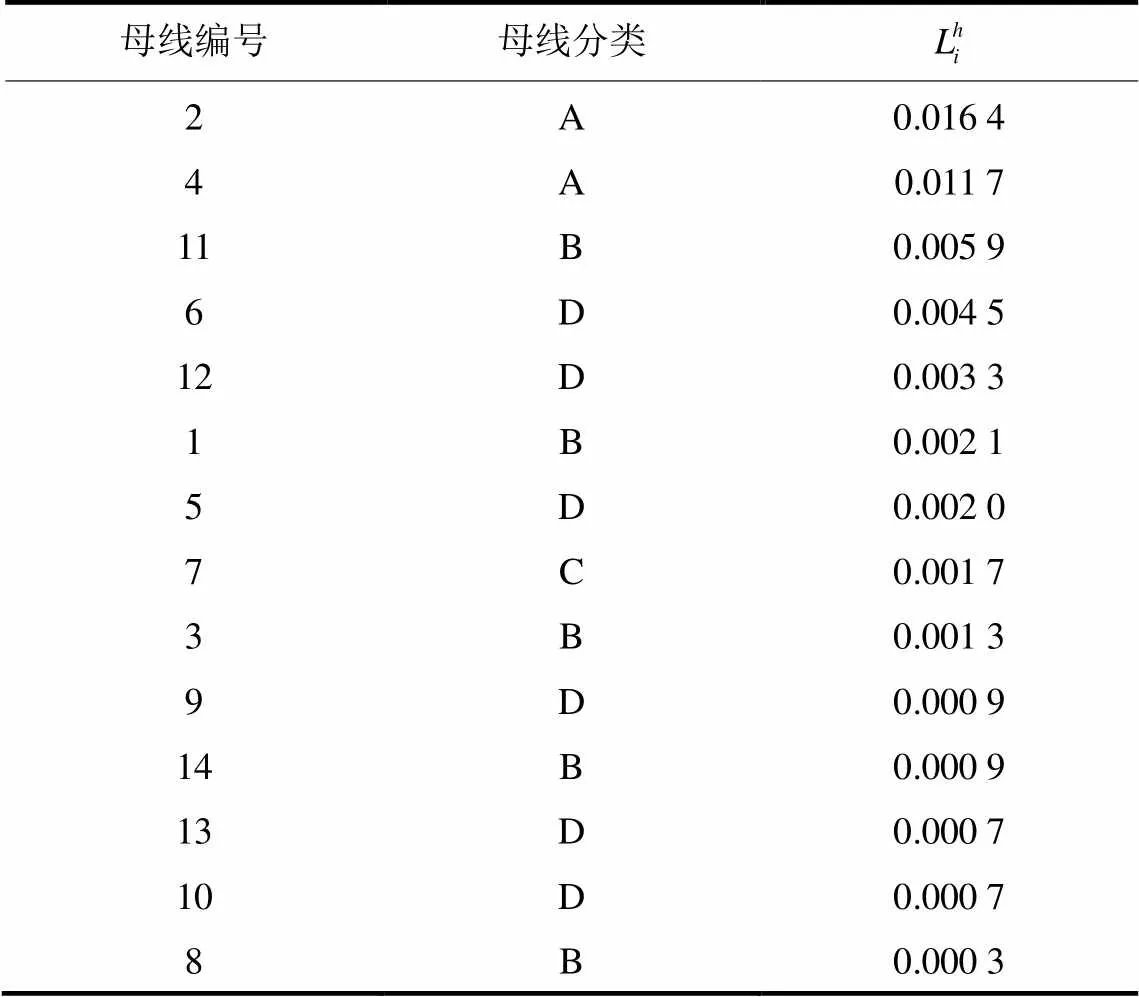
Table 7 Survey priority ranking of the buses (case 2)

本算例在IEEE 14节点的基础上根据实际情况进行部分修改，通过指标法选取谐波量测装置的最优安装位置。算例表明，即便是中等规模的配电网指标法对于减少不可观测母线数量的效果十分明显。对于拓扑比较小的系统而言，指标法足以使的系统完全可观测，而对于较为复杂的系统则需要借助BPSO来达成该目标。

本文提出的谐波源定位方法不仅可以确定谐波源的位置，也能估计各个谐波源的渗透率。从表4、表5可以看出，母线2、4、11被准确定位出来，母线9则由于其谐波电流注入较小而被认为不含谐波源。随后利用定位指标来估计各个非线性母线的谐波源的渗透率大小，并且根据该指标值排列需要进行现场勘测的母线的优先级。在仅仅考虑建模误差时，谐波源位置与谐波源的谐波电流注入水平均可以被准确的定位与估计出来，而在额外考虑测量误差后，则可能导致一定的误判断，从而增加需要进行现场勘测的母线的数目。

5 结论

本文提出了一种基于实测数据的谐波源定位方法。考虑了一定的建模及测量误差，根据各母线的谐波功率以及母线阻抗之间的符号关系，对母线进行了分类。并利用定位指标值对母线排序，得到最为可能的谐波源位置。在ETAP12.6环境下建立了IEEE 14节点系统进行了仿真分析，算例表明，仅考虑负荷建模误差，该方法分类母线直观，定位指标清晰地反映各母线的谐波电流注入水平，可以简单准确将谐波源定位出来。同时考虑建模及测量误差，本文也因其对谐波源定位的影响进行了分析，并证明了该方法仍然是可行的。

[1] HEYDT G T. Identification of harmonic sources by a state estimation technique[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 569-576.

[2] DU Z P, ARRILLAGA J, WATSON N R, et al. Identification of harmonic sources of power systems using state estimation[J]. IEE Proceedings-Generation, Transmission and Distribution, 1999, 146(1): 7-12.

[3] MELIOPOULOS A P S, FAN Z, ZELINGHER S. Power system harmonic state estimation[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1701-1709.

[4] 蔡明, 唐昆明, 张太勤. 基于参数辨识方法的谐波源定位[J]. 电网技术, 2011, 35(6): 134-138.

CAI Ming, TANG Kunming, ZHANG Taiqin. Harmonic source localization based on parameter identification[J]. Power System Technology, 2011, 35(6): 134-138.

[5] 周末, 王果, 常文寰, 等. 适于电气化铁路的三相两臂混合有源补偿研究[J]. 电力系统保护与控制, 2015, 43 (13): 100-104. ZHOU Mo, WANG Guo, CHANG Wenhuan, et al. Study on hybrid active compensation based on three-phase two-leg inverter for electrification railway[J]. Power System Protection and Control, 2015, 43(13): 100-104.

[6] 艾永乐, 郑建云. 基于有功功率贡献量的主谐波源定位[J]. 电力系统保护与控制, 2015, 43(7): 16-22. AI Yongle, ZHENG Jianyun. Localization of the main harmonic source based on the harmonic active power contributions[J]. Power System Protection and Control, 2015, 43(7): 16-22.

[7] 王允建, 陈丰. 基于信息熵的多谐波源定位研究[J]. 电力系统保护与控制, 2015, 43(14): 35-40. WANG Yunjian, CHEN Feng. Research on multiple harmonic sources localization based on information entropy[J]. Power System Protection and Control, 2015, 43(14): 35-40.

[8] 杨源, 林圣, 臧天磊, 等. 基于改进稀疏表示法的谐波源定位[J]. 电网技术, 2013, 37(5): 1279-1284.

YANG Yuan, LIN Sheng, ZANG Tianlei, et al. Improved sparse representation-based location of harmonic sources in power system[J]. Power System Technology, 2013, 37(5): 1279-1284.

[9] HUAIWEI L. Power System Harmonic state estimation and observability analysis via sparsity maximization[J]. IEEE Transactions on Power Systems, 2007, 22(1): 15-23.

[10] 孙国强. 基于相量测量的电力系统状态估计研究[D]. 南京: 河海大学, 2005.

SUN Guoqiang. State estimation study based on phasor measurement[D]. Nanjing: Hohai University, 2005.

[11] GURSOY E, NIEBUR D. Harmonic load identification using complex independent component analysis[C] // Power & Energy Society General Meeting, 2009. PES '09. IEEE, Calgary, Canada, 2009: 1.

[12] GURSOY E, NIEBUR D. Harmonic load identification using complex independent component analysis[J]. IEEE Transactions on Power Delivery, 2009, 24(1): 285-292.

[13] 黄奂, 吴杰康. 基于独立分量分析的电力系统瞬时电压畸变信号判别方法[J]. 电网技术, 2009, 33(6): 5-12.

HUANG H, WU J K. A method to recognize power system instantaneous voltage distortion signal based on independent component analysis[J]. Power System Technology, 2009, 33(6): 5-12.

[14] 谢庆, 张丽君, 程述一, 等. 快速独立分量分析算法在局放超声阵列信号去噪中的应用[J]. 中国电机工程学报, 2012, 32(18): 160-166.

XIE Qing, ZHANG Lijun, CHENG Shuyi, et al. Application of the FastICA algorithm to PD ultrasonic array signal de-noising[J]. Proceedings of the CSEE, 2012, 32(18): 160-166.

[15] DONG-JUN W, SEUNG-IL M. Optimal number and locations of power quality monitors considering system topology[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 288-295.

[16] CARTA A, LOCCI N, MUSCAS C. A PMU for the measurement of synchronized harmonic phasors in three-phase distribution networks[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(10): 3723-3730.

(编辑 张爱琴)

A harmonic sources localization method based on measured data

WANG Ling, CHEN Hongkun, WANG Zhicheng, XU Kun

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

For dividing harmonic responsibility so that dealing with harmonic problems by using economics means, this paper presents a method to identify the harmonic sources based on the data measured by the harmonic measurement devices. According to the connectivity between each nodes, the optimal number and location of harmonic measurement devices are obtained by using the method combined BPSO and index method. Considering a certain modeling and measurement error, it categorizes the suspect buses based on the direction of harmonic power flow, and proposes localization index to rank the bus in order to reduce the field investigation works which is unnecessary. Finally, the IEEE 14 nodes model in ETAP 12.6 is built and the effectiveness of the method proposed is proved.

optimization of harmonic measurement devices; BPSO; harmonic power flow; harmonic sources localization; location index

10.7667/PSPC151187

2015-07-10；

2015-10-16

王 岭(1991-)，男，硕士研究生，研究方向为电力系统运行与控制；E-mail: wlwhu@outlook.com

陈红坤(1967-)，男，工学博士，教授，研究方向为电力系统运行与控制；

王志成(1991-)，男，硕士研究生，研究方向为电气工程。