基于鲁棒方差优化的电力系统频率控制研究

陈 晨，李平康，贾智州



基于鲁棒方差优化的电力系统频率控制研究

陈 晨，李平康，贾智州

(北京交通大学机械与电子控制工程学院，北京 100044)

随着新能源发电大规模并网，随机负荷扰动给电力系统稳定优化运行提出了新的挑战。针对自动发电控制过程中存在的随机扰动和参数摄动的问题，提出了一种基于鲁棒方差约束的状态反馈控制器的参数优化方法。根据鲁棒方差控制(Robust Variance Control，RVC)中不等式约束条件，分析了闭环系统在抑制随机扰动和提高阶跃扰动响应动态性能之间的博弈关系。构造了融合稳态状态方差和控制能量输出约束的优化问题，利用线性矩阵不等式(Linear Matrix Inequality，LMI)获得了鲁棒方差控制器参数。在此基础上，对配置的区域极点圆心坐标值和正标量两个参数进行遗传优化，得到性能指标最优的控制策略。以两区域电力系统模型为例，表明该方法能够有效抑制随机扰动并保持良好的控制性能和鲁棒性能。

负荷扰动；频率控制；鲁棒方差约束；参数摄动；遗传优化

0 引言

作为自动发电控制(Automatic Generation Control, AGC)系统的重要组成部分之一，负荷频率控制(Load Frequency Control, LFC)是保障发电功率和用电负荷之间动态平衡和频率恒定的最主要手段[1]。对于不断变化的用电负荷，AGC系统既要满足自身区域用电负荷的需求，又要考虑到区域之间的功率支援[2]。与此同时，面对我国日益严峻的治霾形势和节能减排目标，火电在一定程度上被水电、风电和光伏发电等清洁能源替代。大规模间歇性能源并网后，其发电波动特性和频率特性影响了电力系统的频率质量[3-4]。如何降低随机负荷扰动对电网的影响，研究有效的控制手段改善AGC系统的频率调节性能，已成为电力系统面临的新问题。

由于PID控制在工程实践中易于实现且具有良好的控制性能，因此传统的LFC系统多采用PID或者其改进策略。文献[5-6]基于PID提出了不同的控制策略，增强了电力系统的鲁棒性和抗干扰性。随着电网互联程度日益加深，不少学者开始关注如何提高频率控制的动态性能，研究了各种控制及优化方法在该领域的应用。文献[7]结合线性矩阵不等式和遗传算法设计了互联LFC系统的基于∞鲁棒约束的PI控制器，证明了所提方法可以有效抑制随机和阶跃干扰。但在自动发电控制过程中，不仅要考虑不同扰动对电力系统稳定运行带来的冲击，更值得关注的是发电机出力速度限制引起的非线性和系统参数摄动引起的不确定性[8-10]。文献[8]将发电机出力约束考虑成饱和环节，分析了鲁棒负荷频率控制器控制性能的影响。文献[9]基于三区域电力系统模型，研究了对于限制发电机功率增量的情况下，系统参数改变+10%，投入0.5倍基准容量的负载时，利用模型预测控制实现了很好的抗干扰性。文献[10]则是针对电力系统结构参数具有不确定性的问题，设计了滑模控制系统。但是先进的控制策略被引入LFC系统后，在分析扰动影响时，一般会将负荷扰动量视为阶跃定常扰动[2,11]。然而，在新能源发电大规模并网的新环境下，其“间歇性”发电的特点扩大了随机负荷干扰对电网的影响。对于新能源发电出力尚无较为成熟的手段进行控制，其带来的系统频率偏差由本区域电网中的常规发电机组进行调节[12]。针对参数摄动和随机干扰两个难题，本文基于鲁棒方差控制(Robust Variance Control，RVC)中不等式约束条件，提出了一种基于鲁棒方差约束的状态反馈控制器的参数优化方法。

鲁棒方差控制是一种兼顾了抑制高斯白噪声扰动同时又保证动态性能的控制策略[13]。但传统RVC要求外部扰动项是具有单位方差的零均值白噪声过程，但实际上扰动并非都是零均值的白噪声，因此不利于该控制策略应用到实际系统中[14]。鉴于此，本文研究了RVC设计时给定的系统稳态状态方差值和闭环极点区域约束之间的关系，改善了传统RVC对于外部扰动的限制，使其外部扰动项不局限于单位方差的高斯白噪声信号。为了保证系统具有良好的动态性能和较小的输出稳态状态方差，构造了融合最小稳态状态方差和控制能量输出的约束条件，将不等式的可行解问题转化为鲁棒优化问题。通过线性矩阵不等式(Linear Matrix Inequality，LMI)技术求解得到状态反馈控制器参数后，对影响闭环系统动态性能指标的闭环极点区域圆心坐标值和正标量进行遗传优化，寻找动态性能最优的控制参数。最后，以两区域LFC系统为例，证明了所提方法具有较强的鲁棒性并对不同的扰动能够有效抑制。

1 两区域互联电力系统模型

现代电网表征为多区域协调电力系统，区域电网不仅要考虑内部的发电功率与负荷之间的平衡关系，而且要关注区域间的交互联系。当电力系统遭受强烈的随机负荷扰动时，发电侧的功率平衡有可能被打破，进而导致LFC调控能力下降，严重时造成区域内发电机间失去同步，此时电力系统的功率及频率会发生强烈的振荡，造成电网崩溃或区域电网解列的严重事故。本文以两区域电网为例，重点研究随机负荷扰动和参数摄动对互联区域的影响。

两区域LFC系统由调速器、原动机、发电机和负荷等环节组成，并在此基础上增加了不同区域间的功率交换环节，其动态模型如图1所示[15]。图1中，和为调速器有差调节系数，和为频率偏差系数，和为积分控制增益，和为汽轮机时间常数，和为调速器时间常数，和为电力系统时间常数，和为电力系统增益，为联络线同步系数。本文所设计控制器是以状态反馈的形式得以实现，为此选择系统各个子环节的输出Δƒ、ΔGi、ΔGi、ʃACE、Δtie(=1, 2)作为系统的状态变量，分别代表各区域的电网频率偏差、原动机输出功率变化量、调速器阀门位置变化量、控制区域误差变化积分值及联络线上的净交换功率偏差值。状态变量=[Δƒ1, ΔG1, ΔG1, ʃ1, Δtie, Δƒ2, ΔG2, ΔG2, ʃ2]。

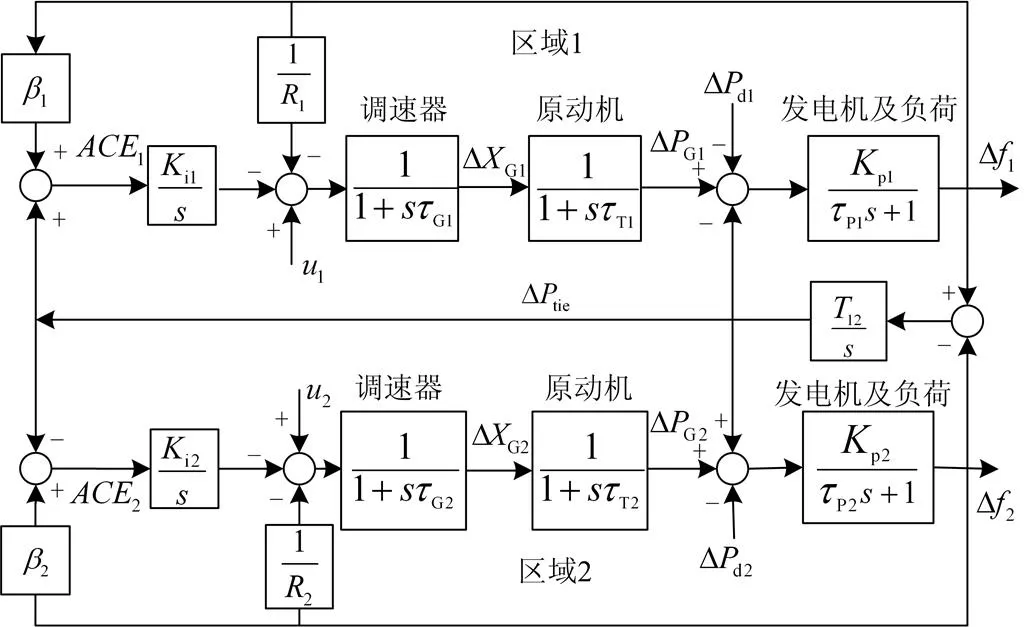
图1 含有积分控制器的两区域LFC系统框图

由图1得到系统的状态方程表达式为

；

。

2 基于方差约束的鲁棒优化算法

2.1 鲁棒方差约束的最优控制

当系统存在参数摄动和随机扰动时，鲁棒方差控制可以实现方差和区域极点约束，通过给定状态的稳态方差上界和配置区域极点来保证闭环系统具有期望的稳态性能和动态性能。

首先考虑含有随机扰动项()的闭环系统，如式(3)所示。

令=+。如果系统(3)是渐近稳定的，则闭环系统的稳态状态方差矩阵=limE[()T()]存在，且满足以下的Lyapunov方程[17]：

闭环系统的所有极点在复平面上都位于以(-, 0)为圆心，以为半径的圆盘内，存在不等式约束条件[13]：

通过式(5)可以看出，传统RVC的不等式条件在实现极点配置的同时，增加了随机扰动项，加入随机扰动项会影响到不等式中的求解，势必会对系统的动态性能产生影响。本文将其改为[18]。

1) 闭环系统的所有极点在复平面上都位于以(-, 0)为圆心，以为半径的圆盘内；

2) 稳态状态方差矩阵对角线上的第个元素，其中是给定的一组稳态方差常数。

若系统含有不确定项(Δ和Δ)，假设Δ和Δ具有如下形式[19]：

引理1[19]：对给定的具有适当维数的矩阵、和，其中是对称的，则对所有满足T<的矩阵满足

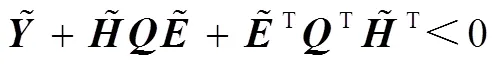
成立，当且仅当存在一个标量>0，使得

综合引理1和式(4)~式(6)，可以推导出鲁棒方差控制设计的不等式矩阵[13]：

则系统(3)的鲁棒方差控制率是()=-1()。式(7)是关于变量、和的一个线性矩阵不等式，但求解结果是满足约束条件的一组可行解，并不是唯一的。本文融合了稳态状态方差和控制能量约束作为最优性能指标，来设计兼顾两者的鲁棒方差控制律，如下：

式(8)可以理解为以最小化稳态状态方差与控制能量的加权作为控制优化的目标。控制器能量的作用是衡量对被控对象的冲击程度，增大可以加强控制器能量的影响，实际选择时，可先令是一个较小的权重矩阵。在控制能量和稳态状态方差之间折衷，使闭环系统具有所期望的动态特性和稳态状态方差，将权重矩阵选定为，。

考虑到<，性能指标的上界为

假设存在矩阵，使得

则trace()的最小化即保证性能指标的最小化，因此根据Schur补引理[19]，可以将不等式(9)转化为线性矩阵不等式的形式为

本文所提的鲁棒方差优化算法增加了新的约束条件(10)，是在文献[13]的RVC的最小能量控制的基础上，补充了稳态状态方差约束条件，通过使得trace()的最小化的方法进一步约束稳态状态方差矩阵，使其对角线元素[]尽量小。将不等式的可行解问题转变成了线性矩阵不等式的凸优化问题，利用Matlab中LMI工具箱内的mincx函数来求解。结合式(7)和式(10)，可将求解鲁棒方差约束的问题表述为如下的优化问题：

传统的鲁棒方差控制大多数通过试凑设定圆心坐标值，其值与标量不同的取值会导出具有不同正定对称矩阵、的鲁棒方差控制率，出现了系统动态性能和稳态状态方差的差异。因此，本文利用遗传优化算法实现对这两个参数的寻优，期望在阶跃扰动的情况下能够获得最优的动态性能。

2.2 基于遗传算法的控制参数优化

电力系统中存在的负荷扰动量是由变化幅值小变化率大的随机分量、变化幅值大的持续扰动分量等组成。因此，在考虑了对随机分量进行有效抑制后，需要进一步分析如何提高闭环系统的动态性能。本文采用浮点编码方式的遗传算法优化控制器参数，构造了与闭环极点圆心坐标值及标量两个参数相关的优化问题。浮点编码方式不需编、解码操作，有效提高了运算效率及精度，染色体字符串为[,]。

遗传算法并不需要知道优化问题本身的任何信息，在进化过程中得到具有最大适应度函数值的个体作为最优解输出。求解式(11)，并将得到的鲁棒方差控制率代入闭环系统数学模型中，假设系统中只存在阶跃定常扰动，本文取Δd=[0.1, 0]T，仿真得到控制输入和状态输出。计算此时消耗的控制能量和状态变量的瞬态响应的加权和作为动态性能指标。

1) 建立在参数摄动矩阵Δ和Δ且存在干扰矩阵w情况下的不确定线性模型。

3) 设置遗传算法参数[,]的取值范围，将步骤(2)中求解的控制器参数代入Simulink模型中，优化求解式(12)的优化问题。本文取群体大小为200，进化代数为150。

4) 得到最优的和值及相应的反馈控制率=-1。

3 算法仿真验证

两区域电力系统参数设置如下[15]：，，，p.u.，随机负荷扰动强度值为0.01。系统参数的变化范围：，，，，(=1, 2)。我国允许的电网频率偏差为±0.2 Hz，本文考虑到电力系统的动态性能，使用系统参数变化范围的±10%作为设计值。同时，兼顾LFC闭环系统的动态性能和稳态状态方差，假定状态变量稳态方差上限值均为1。

图2和图3对比了最小能量约束(MN)和本文所提的融合稳态状态方差和控制能量输出约束(MVMN)两种约束条件。从图2中可以看出，、的变化会影响稳态状态方差的上界，MVMN有更小的稳态状态方差上界值。在随机扰动情况下，系统状态输出应有更小的方差值。同时，图3证明了MVMN约束会提高闭环系统的控制能量上界值，使系统具有了较大的控制能量，但、的变化能够帮助MVMN改善系统输出的动态性能。

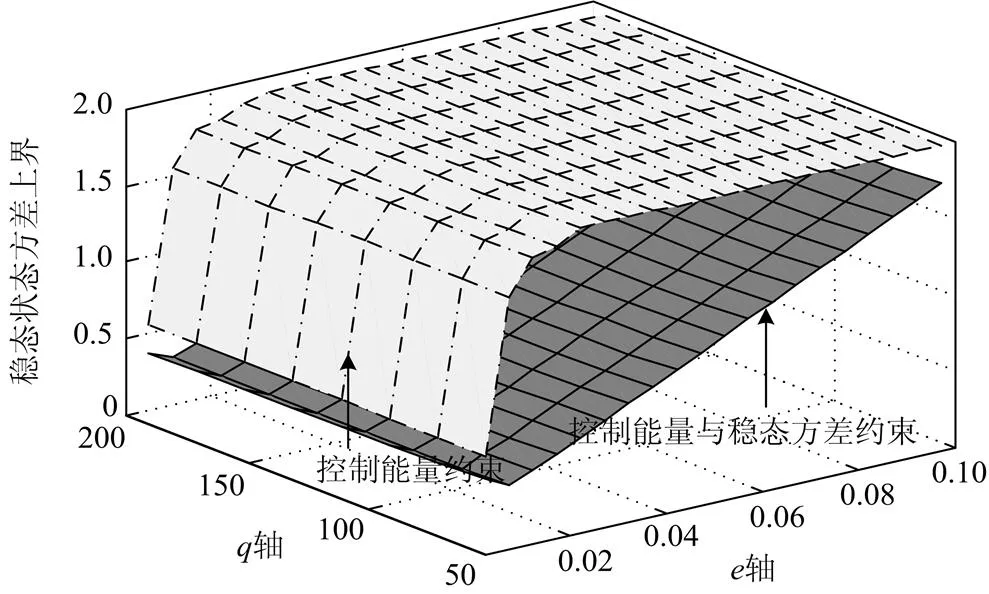
图2 ε、q和稳态状态方差上界的关系

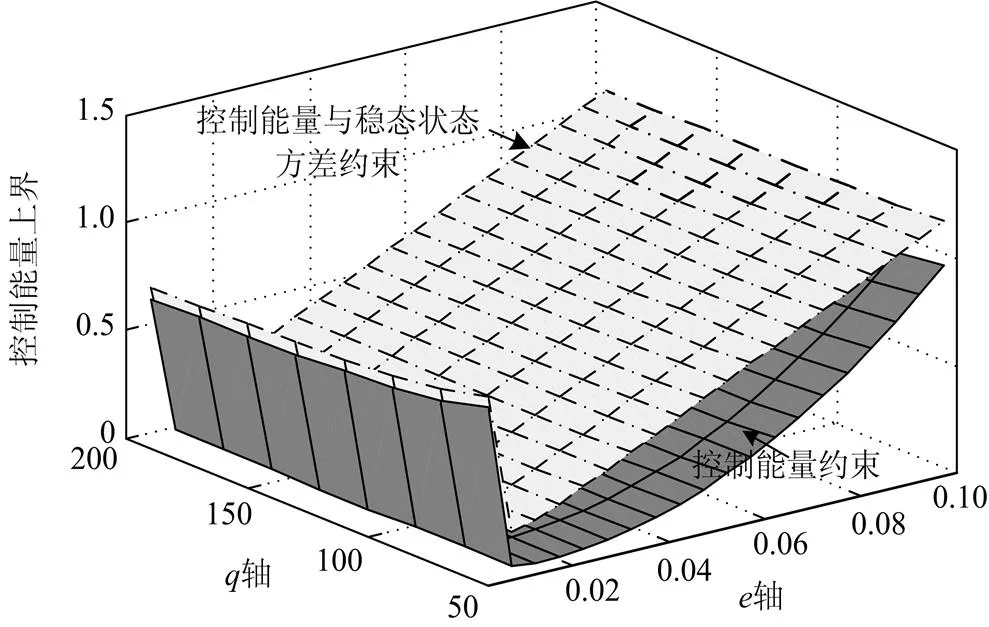
图3 ε、q和控制能量上界的关系

遗传算法优化参数和的优化区间分别为[0.002, 0.1]和[50, 200]。根据本文所提的鲁棒方差控制率(MVMN-RVC)的方法步骤，优化结果：= 199.5，=0.099 7，得到系统的控制器输出为

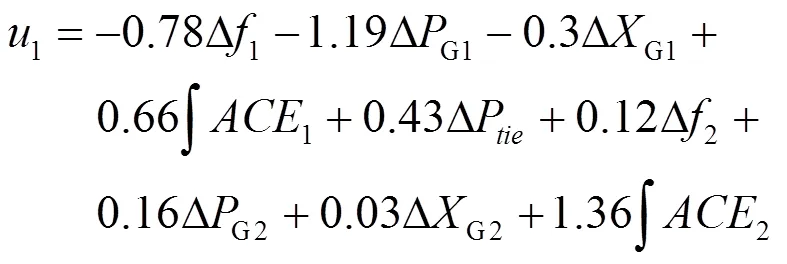
假设电力系统区域1中出现方差为1.0且幅值为3.0左右的高斯白噪声。通过图4可以看出，在区域1产生随机扰动后，通过联络线将随机负荷的扰动影响传递到了区域2。但图中系统的频率偏差输出都有较大的衰减，其中区域1中Δƒ1的方差为0.08，波动幅值降为1.0左右，区域2中Δƒ2的方差为0.012，波动幅值降为0.3左右。从电力系统输出的角度来看，说明所提方法对噪声产生了很好的抑制作用。

选取相同的闭环极点区域圆心值，选取优化区间的最小值，文献[13]所提的具有最小能量约束的鲁棒方差控制率(MN-RVC)的控制器输出为

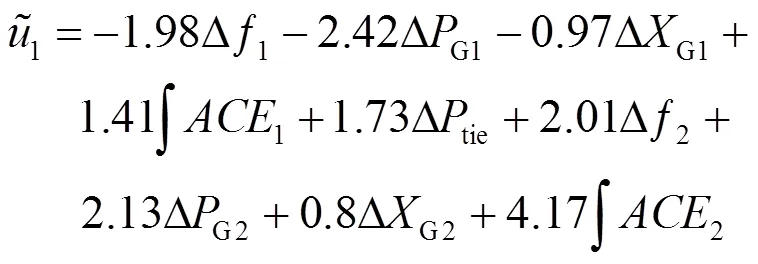
同时，本文与文献[15]中的控制策略进行了对比研究，讨论了在电力系统区域1出现0.1 p.u.的负荷扰动时，两区域电网频率变化情况。图5和图6分别为区域1和区域2在阶跃负荷扰动下系统的动态响应。应用本文所提的方法，区域1的Δƒ1能在5 s的时间恢复正常。同时，扰动波及到区域2，使其频率出现了偏移，但在7 s左右也恢复为零。通过对比阶跃扰动的动态响应图，可以看出MVMN- RVC在抑制随机噪声的基础上，能够取得较为理想的动态性能。

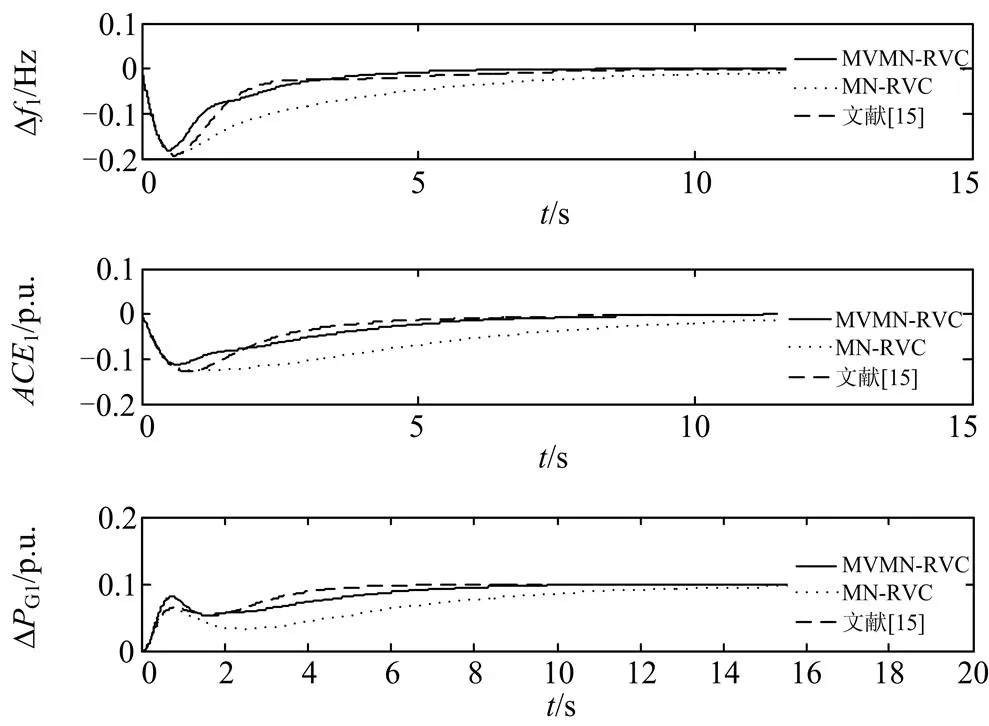
图5区域1阶跃负荷扰动下系统的动态响应

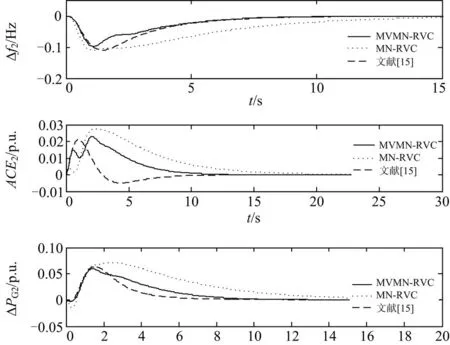
图6区域2阶跃负荷扰动下系统的动态响应

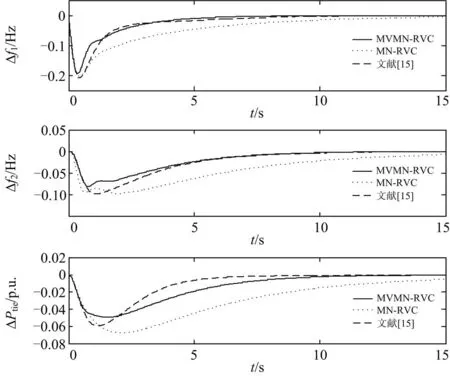
图7 参数摄动和阶跃负荷扰动下系统的响应

4 结论

本文提出了一种基于遗传优化的鲁棒方差约束改进算法，研究了鲁棒方差约束条件中系统稳态状态方差值和闭环极点区域约束之间的关联。通过构造融合最小稳态状态方差和控制能量输出的约束条件，将不等式的可行解问题转化为鲁棒优化问题。传统的鲁棒方差控制大多数通过试凑设定值，本文利用遗传优化寻找阶跃扰动响应动态性能最优的控制参数，解决了和的选取问题。最后以两区域电力系统为对象，分别在随机扰动、阶跃扰动和参数摄动的情况下，仿真证明了所提算法能够衰减噪声并且具有较强的鲁棒性和动态性能。

[1] 于汀, 蒲天骄, 刘广一, 等. 电网AGC与AVC协调控制方法[J]. 电力系统保护与控制, 2015, 43(15): 42-47.

YU Ting, PU Tianjiao, LIU Guangyi, et al. Coordinated control method of AGC and AVC in power grid[J]. Power System Protection and Control, 2015, 43(15): 42-47.

[2] 叶荣, 陈皓勇, 卢润戈. 基于微分博弈理论的两区域自动发电控制协调方法[J]. 电力系统自动化, 2013, 37(18): 48-54, 67.

YE Rong, CHEN Haoyong, LU Runge. A differential games theory based method for coordinating two-area automatic generation control[J]. Automation of Electric Power Systems, 2013, 37(18): 48-54, 67.

[3] 包宇庆, 李扬, 王春宁, 等. 需求响应参与大规模风电接入下的电力系统频率调节研究[J]. 电力系统保护与控制, 2015, 43(4): 32-37.

BAO Yuqing, LI Yang, WANG Chunning, et al. On demand response participating in the frequency control of the grid under high wind penetration[J]. Power System Protection and Control, 2015, 43(4): 32-37.

[4] 于汀, 王玮, 蒲天骄, 等. 风电高渗透率下中长期时间尺度系统频率波动仿真研究[J]. 电网与清洁能源, 2014, 30(1): 87-93, 108.

YU Ting, WANG Wei, PU Tianjiao, et al. Study of the medium-term and long-term time-scale system frequency fluctuations simulation under high penetration of wind power[J]. Power System and Clean Energy, 2014, 30(1): 87-93, 108.

[5] PADHAN D G, MAJHI S. A new control scheme for PID load frequency controller of single-area and multi-area power systems[J]. ISA Transactions, 2013, 52(2): 242-251.

[6] 孔繁镍, 李啸骢, 吴杰康, 等. 基于尼科尔斯 PID 设计方法的负荷频率控制[J]. 中国电机工程学报, 2012, 32(22): 79-85.

KONG Fannie, LI Xiaocong, WU Jiekang, et al. Design of Nichols PID controller for load frequency control[J]. Proceedings of the CSEE, 2012, 32(22): 79-85.

[7] RERKPREEDAPONG D, HASANOVIĆ A, FELIACHI A. Robust load frequency control using genetic algorithms and linear matrix inequalities[J]. IEEE Transactions on Power Systems, 2003, 18(2): 855-861.

[8] WANG Y, ZHOU R, WEN C. Robust load frequency controller design for power system[J]. Generation Transmission and Distribution, IEE Proceeding C, 1993, 140(1): 11-16.

[9] 杨罡, 刘明光, 屈志坚. 基于MPC算法的电力系统负荷频率控制[J]. 北京交通大学学报, 2012, 36(2): 105-110.

YANG Gang, LIU Mingguang, QU Zhijian. Load frequency control of power systems based on MPC algorithm[J]. Journal of Beijing Jiaotong University, 2012, 36(2): 105-110.

[10] 米阳, 吴晓, 楚瀛, 等. 基于滑模控制的单域电力系统负荷频率控制[J]. 控制与决策, 2012, 27(12): 1881-1884, 1889.

MI Yang, WU Xiao, CHU Ying, et al. Load frequency control for one area power systems based on sliding mode control[J]. Control and Decision, 2012, 27(12): 1881-1884, 1889.

[11] 田启东, 翁毅选. 基于CPS标准的互联电网最优自动发电控制策略研究[J]. 电网与清洁能源, 2015, 31(6): 33-38.

TIAN Qidong, WENG Yixuan. Research of the optimal automatic generation control strategy of interconnected power grid based on CPS standard[J]. Power System and Clean Energy, 2015, 31(6): 33-38.

[12] 李中豪, 黄屹俊, 张沛超, 等. 大型风燃协调等效电厂的自动发电控制策略研究[J]. 电力系统保护与控制, 2016, 44(4): 44-50.

LI Zhonghao, HUANG Yijun, ZHANG Peichao, et al. A study about the automatic generation control strategy of large scale wind-gas coordinating equivalent power plant[J]. Power System Protection and Control, 2016, 44(4): 44-50.

[13] 俞立. 具有区域极点和方差约束的不确定连续系统鲁棒控制[J]. 自动化学报, 2000, 26(4): 509-514.

YU Li. Robust control of uncertain systems with regional pole and variance constrains[J]. Acta Automatica Sinica, 2000, 26(4): 509-514.

[14] 吴春, 齐蓉. 永磁同步电机伺服系统混合鲁棒方差控制[J]. 电机与控制学报, 2013, 17(5): 63-68.

WU Chun, QI Rong. Mixed robust variance control designof PMSM servo system[J]. Electric Machines and Control, 2013, 17(5): 63-68.

[15] RAY G, PRASAD A N, PRASAD G D. A new approach to the design of robust load-frequency controller for large scale power systems[J]. Electric Power Systems Research, 1999, 51(1): 13-22.

[16] 刘咏飞, 鞠平, 薛禹胜, 等. 随机激励下电力系统特性的计算分析[J]. 电力系统自动化, 2014, 38(9): 137-142.

LIU Yongfei, JU Ping, XUE Yusheng, et al. Calculation analysis on power system characteristics under random excitation[J]. Automation of Electric Power Systems, 2014, 38(9): 137-142.

[17] 王子栋, 郭治. 含结构参数扰动的线性连续系统的鲁棒约束方差控制[J]. 自动化学报, 1996, 22(5): 538-544.

WANG Zidong, GUO Zhi. Robust constrained variance control for linear continuous systems with structured parameter perturbation[J]. Acta Automatica Sinica, 1996, 22(5): 538-544.

[18] 王远钢, 郭治. 状态反馈中圆形极点与状态方差约束的相容性[J]. 自动化学报, 2001, 27(2): 207-213.

WANG Yuangang, GUO Zhi. Consistency of circular pole and state variance constraints in state-feedback control[J]. Acta Automatica Sinica, 2001, 27(2): 207-213.

[19] 俞立. 鲁棒控制: 线性矩阵不等式处理方法[M]. 北京:淸华大学出版社, 2002.

(编辑 魏小丽)

Frequency control for power systems based on robust variance optimization

CHEN Chen, LI Pingkang, JIA Zhizhou

(School of Mechanical and Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China)

With the large-scale grid interconnection of the new energy power generation, stochastic load disturbance gives the new challenges about how to maintain the stability and optimization operation of power systems. For the problems of stochastic load disturbance and parameter uncertainties in automatic generation control process, a parameter optimization algorithm of the state feedback controller based on robust variance constraint is proposed. Based on the inequality constraints of robust variance control principles, the game relationship between stochastic disturbance rejection and dynamic performance improvement of step disturbance response of closed loop system is analyzed. The constrained optimization problems considering steady state variance and control energy output constraint is constructed and LMI is used to design the controller parameters. Using genetic algorithm, closed loop poles circle center and positive scalar are optimized to design the control strategy with the optimal performance index. Two-area power system model is provided to demonstrate that the presented method can effectively restrain stochastic load disturbance and have good control performance and robustness.

load disturbance;frequency control;robust variance constraint;parameter perturbations;genetic optimization

10.7667/PSPC151408

2015-08-11；

2016-02-21

陈 晨(1986-)，男，博士研究生，研究方向为电力系统的智能控制以及优化；E-mail: 10116302@bjtu.edu.cn

李平康(1955-)，男，通信作者，博士，教授，研究方向为与电力生产过程相关的建模、仿真及测控方面的理论；E-mail: pkli@bjtu.edu.cn

贾智州(1990-)，男，博士研究生，研究方向为智能控制以及优化理论。E-mail:13116341@bjtu.edu.cn