加性信号输入时单模激光损失模型的平均光强相对涨落

叶 庆，卿秀华



加性信号输入时单模激光损失模型的平均光强相对涨落

叶 庆，卿秀华

（武汉纺织大学 电子与电气工程学院，湖北 武汉 430073）

运用线性化近似方法，采用色泵噪声和实虚部间关联的量子噪声驱动的单模激光损失模型，计算周期信号加性输入时的稳态平均光强关联函数、稳态平均光强相对涨落。发现在信号强度不大、频率较高、小噪声、远离阈值和量子噪声实虚部之间弱关联的条件下，稳态平均光强相对涨落较小，即系统相对稳定。

单模激光；噪声；量子噪声；净增益；稳态平均光强相对涨落

由于量子噪声和泵噪声的存在，激光器工作时总是伴随有涨落的出现。量子噪声和泵噪声之间不同关联形式下激光系统的瞬态和定态性质被众人所研究，发现不同关联形式对激光系统输出性能有较大的影响。同时，减小激光光强涨落，可以增加激光的输出稳定性，提高系统的输出质量,因此对激光光强涨落的研究已成为近年普遍关注的话题。韩立波等人分析了色泵噪声驱动时单模激光增益模型的稳态平均光强相对涨落。偏置信号输入后单模激光系统的平均光强相对涨落也有研究。

本文考虑了量子噪声实部和虚部之间的关联，运用单模激光损失模型和线性化近似方法，计算了反映激光动力学性质的光强关联函数和稳态平均光强相对涨落。同时，由光强相对涨落不但可以分析激光系统的输出稳定性，还可以进一步计算信噪比，反映激光系统的随机共振现象。

1 单模激光系统的平均光强关联函数和稳态平均光强相对涨落

系统噪声满足如下统计性质：

根据稳态平均光强关联函数的定义：

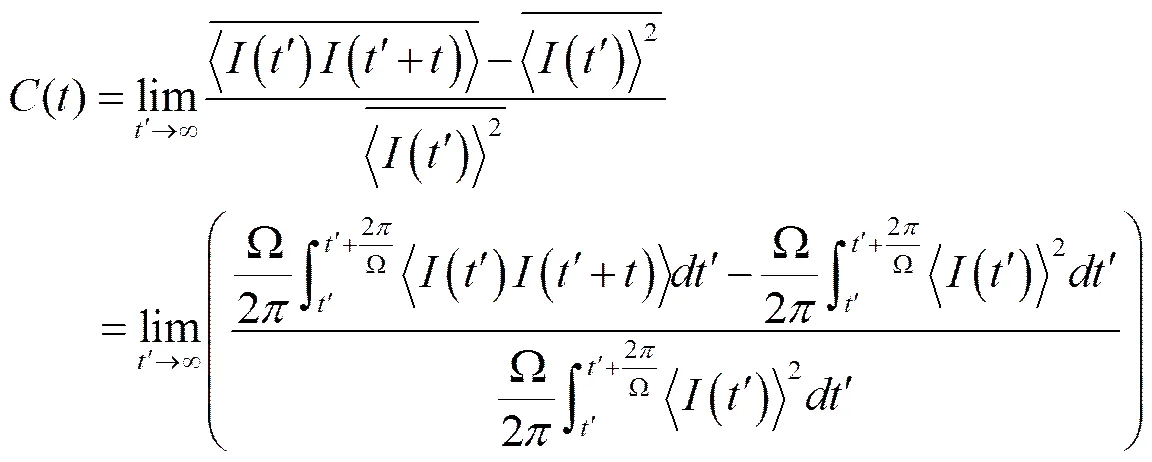
将（3）代入上式，计算得稳态平均光强关联函数为：

2 输入的信号对稳态平均光强相对涨落的影响

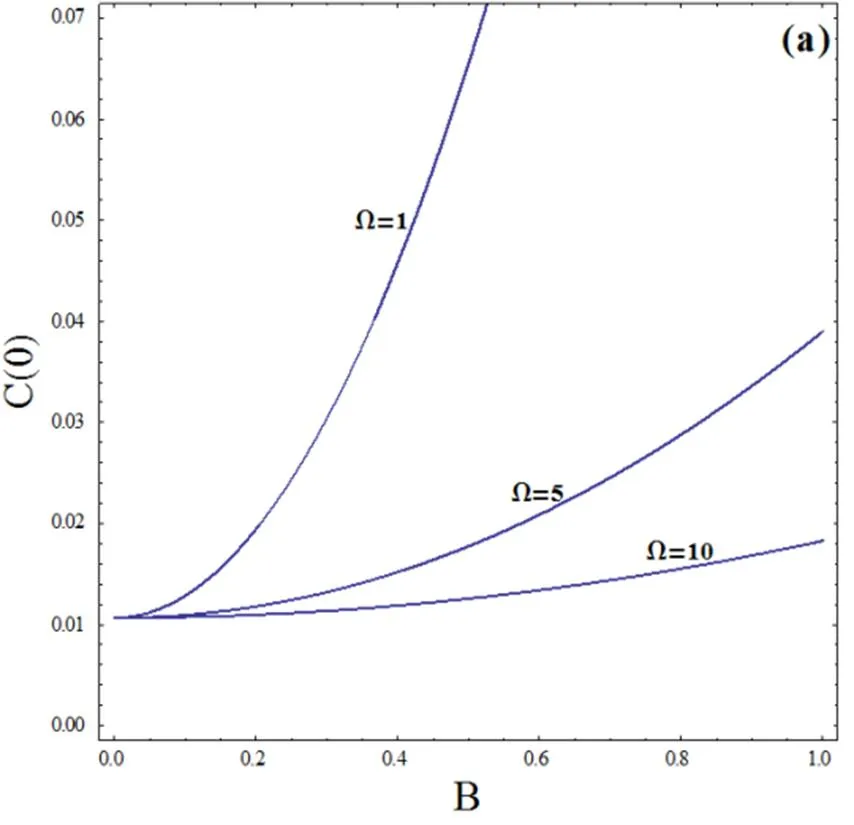
图1（a） 相对涨落与信号振幅的关系曲线（）图1（b） 相对涨落与信号振幅的关系曲线（）

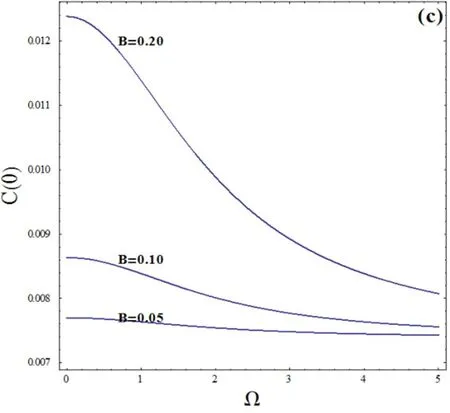
图1（c） 相对涨落与信号频率的关系曲线（）图1（d） 相对涨落与信号频率的关系曲线（）

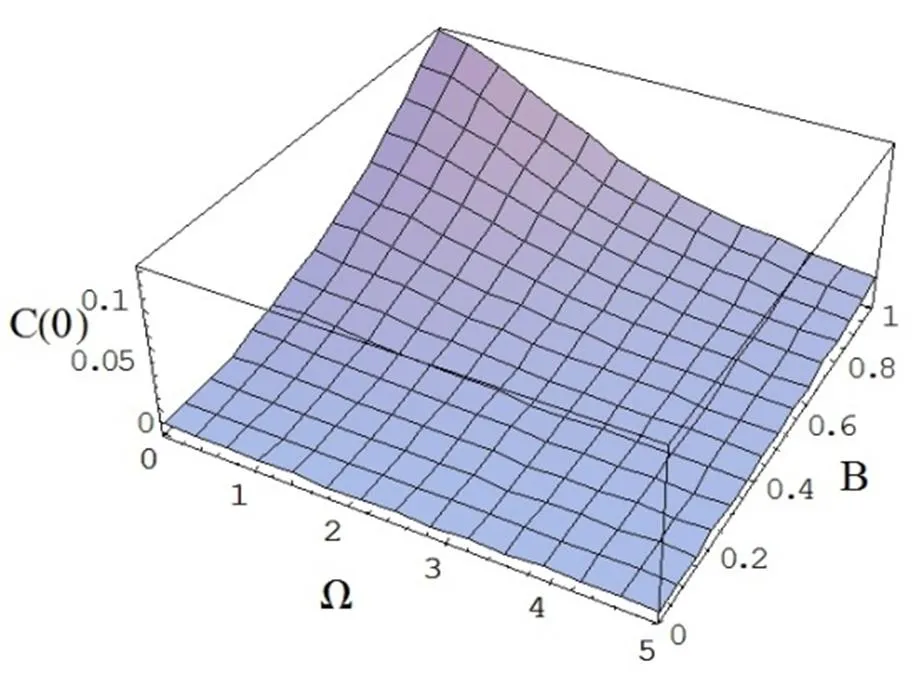
图1（e） 相对涨落与信号频率的关系曲线（）

3 噪声对稳态平均光强相对涨落的影响

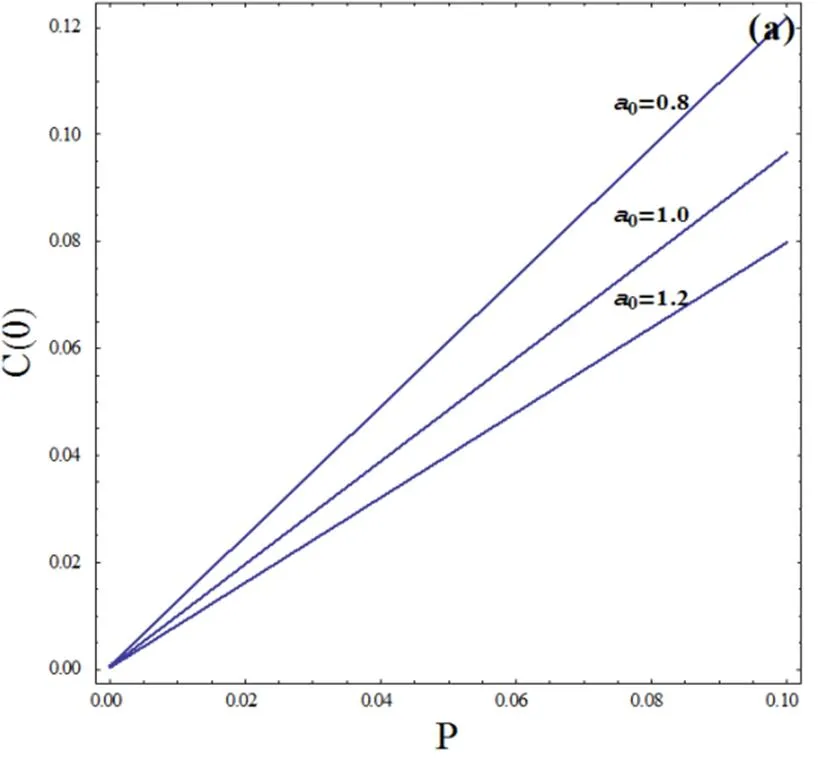
图2（a） 相对涨落与泵噪声强度的关系曲线（）图2（b） 相对涨落与泵噪声强度的关系曲线（）

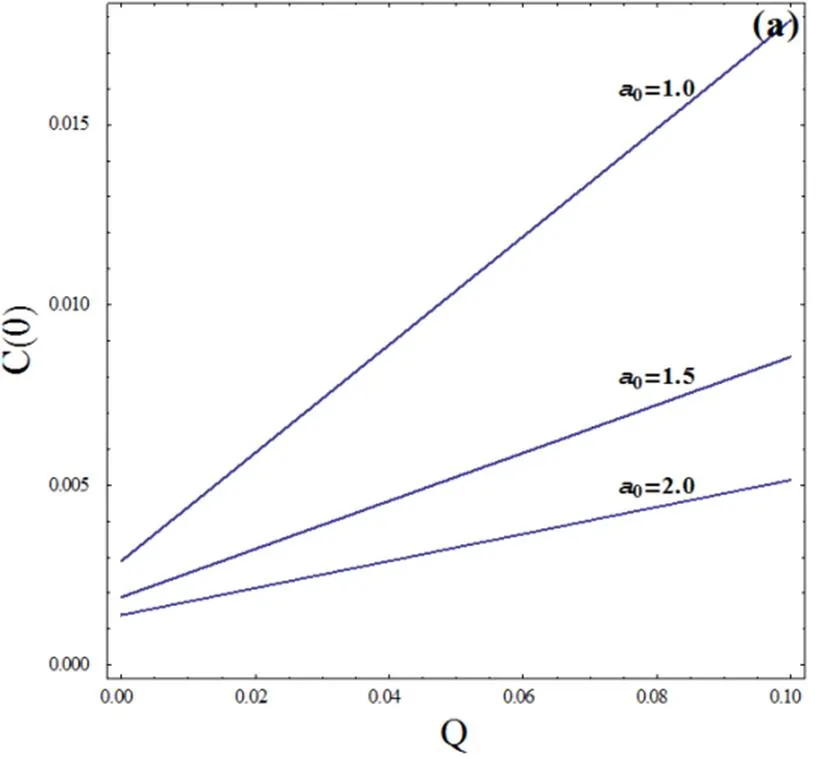
图3（a） 相对涨落与量子噪声强度的关系曲线（）图3（b） 相对涨落与量子噪声强度的关系曲线（）

4 净增益系数和量子噪声实虚部间关联对稳态平均光强相对涨落的影响

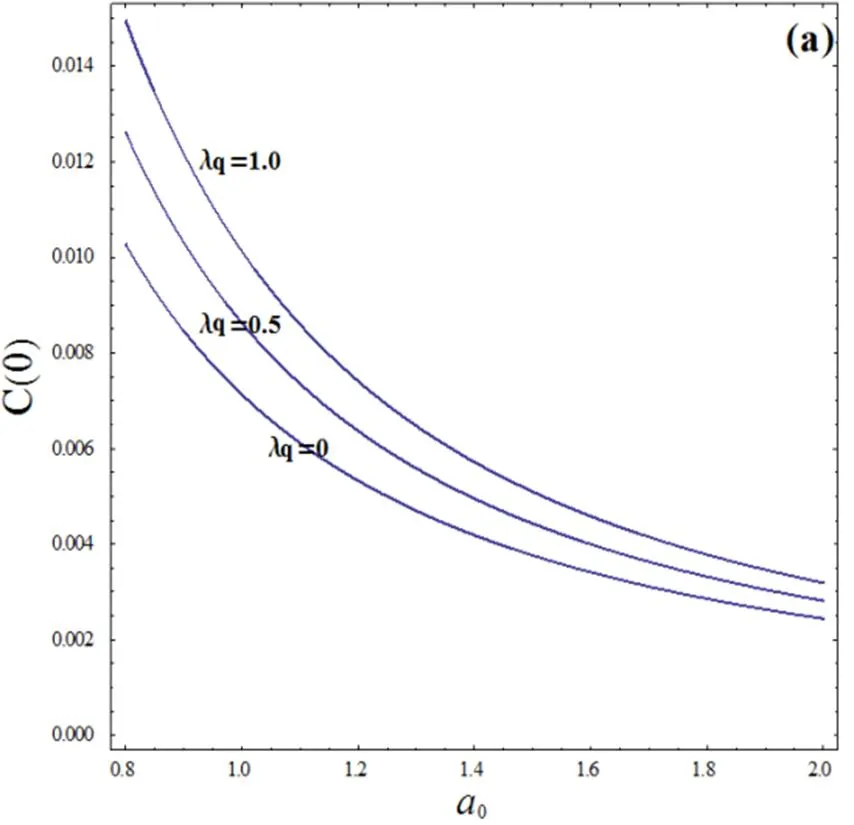
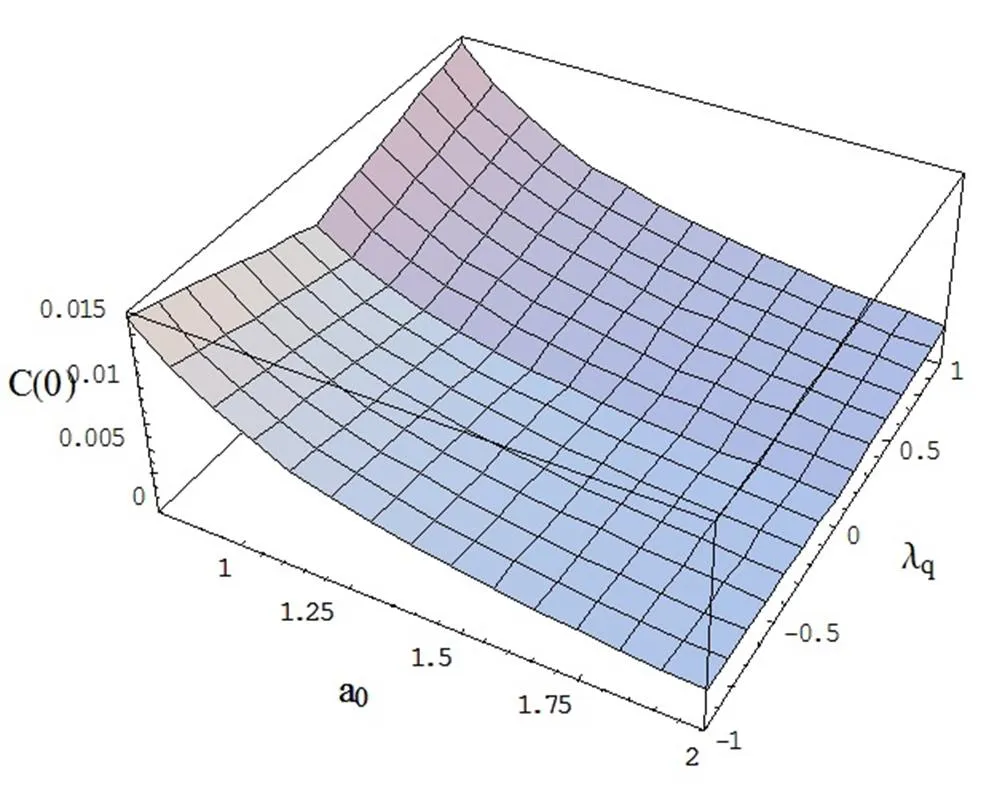
图4 相对涨落与净增益系数和关联系数的关系曲线（）

5 结论

激光系统用稳态平均光强相对涨落来描述系统的稳定性，即涨落越小，系统相对越稳定。综上所述，加性输入的周期信号、噪声及量子噪声间的关联和阈值对系统的稳态平均光强相对涨落有较大的影响。在信号振幅减弱、信号频率增大、量子噪声和泵噪声强度减弱、量子噪声实虚部间弱关联和远离阈值的条件下激光系统的统计涨落较小。

[1] Fulinski A, Telejko．On the effect of interference of additive and multiplicative noise[J]. Physics Letters A，1991，152(1-2)：11-14.

[2] Cao Li, Wu Dajin．Stochastic dynamics for systems driven by correlated noise [J]. Physics Letters A，1994，185(1)：59-64．

[3] Zhu Shiqun．Steady-state analysis of a single-mode laser with correlation between additive and multiplicative noises [J]．Physics Review A, 1993，47(3)：2405-2408．

[4] Zhang Li, Cao Li, Wu Dajin．New amplitude equation of single mode laser[J]．Chinese Physics，2003，12(1)：33-38．

[5] 周小计，曹力，吴大进．关联噪声对单模激光动力学性质的影响[J]．光学学报，1999，19(1)：7-12．

[6] 韩立波，曹力，吴大进，等．信号直接调制色泵噪声的单模激光光强涨落[J]．华中科技大学学报(自然科学版)，2004，32(3)：34-36.

[7] 叶庆，张继龙．单模激光系统的光强相对涨落和功率谱[J]．激光与红外，2016，46(5)：565-569.

[8] Hernandez-Gorcia E, Toral R, San Minguel M. Intensity correlation function for the colored gain-noise model of dye lasers[J]． Physics Review A，1990，42(11)：6823-6830．

[9] Roberto Benzi，Alfonso Sutera，Angelo Vulpiani. The mechanism of stochastic resonance [J]．Journal of Physics A Mathematical and General, 1981，14：453-457．

[10]Ke Shengzhi, Cao Li, Wu Dajin, et al．General laser intensity Langevin Equation in a single-mode laser model [J]．Chinese Physics Letters，2001，18(3)：370-372．

Intensity Fluctuation in the Loss-Noise Model Of Single-Mode Laser with an Input Additive Signal

YE Qing, QING Xiu-hua

(School of Electronic and Electrical Engineering, Wuhan Textile University, Wuhan Hubei 430073, China)

Using the linear approximation method, we calculated the normalized steady-state mean intensity correlation function, the normalized steady-state mean intensity fluctuationin a loss-noise model of single-mode laser system with an input additive signal driven by a colored pump noise and a quantum noise, whose real and imaginary part are cross-correlated. We found thatbecomes lower when the signal has smaller amplitude or higher frequency, the pump noise intensity is smaller, the quantum noise intensity is smaller, the laser system is far from threshold and the cross-correlation between the real and imaginary part of quantum noise is weaker.

single-mode laser; noise; quantum noise; net gain; steady-state mean intensity fluctuation

TN241

A

2095－414X(2016)06－0072－05

叶庆（1982- ），女，讲师，硕士，研究方向：激光物理、统计物理.

国家自然科学基金面上项目（11275157）.