织物透气率、透湿量、毛细效应与悬垂系数的灰色关联性研究

马顺彬，蔡永东



织物透气率、透湿量、毛细效应与悬垂系数的灰色关联性研究

马顺彬，蔡永东

（江苏工程职业技术学院，江苏 南通 226007）

设计生产6款织物，对其透气率、透湿量、经向毛细效应、纬向毛细效应、动态悬垂系数和静态悬垂系数进行测试。然后用灰色系统理论对其关联性进行研究，研究结果表明：影响动态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量；影响静态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量；透气率与悬垂系数之间的线性关系显著。

透气率；透湿量；毛细效应；悬垂系数；灰色系统理论

灰色系统理论是邓聚龙教授提出的，该理论已广泛应用于社会、经济、科技、农业、生态、生物等各个领域[1]。汪学骞等采用灰色关联度评价，排列出对比试样的湿热舒适性的优劣[2]。王健应用灰色系统理论，得出了棉织物结构参数与悬垂系数的关联度，对其进行了排序，认为影响棉织物悬垂性能的最主要三个结构参数依次是紧度、平方米重量及厚度[3]。王瑄运用灰色系统控制理论方法，对金属纤维混纺电磁波屏蔽织物服用性能影响因素进行灰色关联的优势分析[4]。马顺彬对15种竹浆/棉交织物的拉伸性能、撕破性能、耐磨性能等进行了测试，利用灰色聚类分析对其力学性能做了综合评价[5]。刘海运用灰色系统理论对茧丝绸价格指数进行了分析与预测[6]。黄紫娟等应用灰色系统理论，得出了毛织物结构参数与悬垂系数的关联度[7]。本文研究了6款涤棉混纺织物透气率、透湿量、毛细效应与悬垂系数的关联性。

1 试验织物

织物规格与结构参数见表1。为了使试验结果更加具有可比性，采用GA708型喷气织机织造，组织为平纹、2/2斜纹，采用14.6tex涤/棉65/35混纺纱做经纱，纬纱采用14.6tex纯棉纱，经密均为220根/10cm，仅改变纬密（纬密分别为180、190、200根/10cm）。对涤/棉混纺织物的透气率、透湿量、毛细效应和悬垂系数进行了测试。

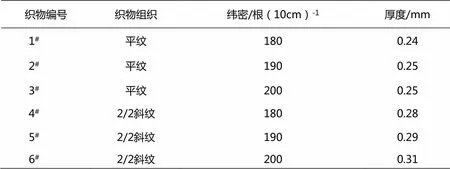
表1 织物规格与结构参数

2 试验仪器及测试方法

试验仪器及测试方法见表2所示。

表2 试验仪器及测试方法

3 灰色关联分析

织物透气率、透湿量、经向毛细效应、纬向毛细效应与悬垂系数的测试结果见表3。影响织物悬垂性能的因素很多，如经纬纱线密度、经纬密度、平方米重量、厚度、紧度等，而受诸多因素影响的织物悬垂性可视为一个“部分信息已知、部分信息未知”的灰色系统，充分利用数量不多的数据和信息寻求相关因素自身与各因素之间的数学关系。

表3 织物透气率、透湿量、经向毛细效应、纬向毛细效应与悬垂系数的测试结果

3.1 确定参数数列和比例

根据灰色系统理论，将织物的透气率、透湿量、经向毛细效应和纬向毛细效应视为一个灰色系统，以表3中的织物的悬垂系数作为参考数列，记为0={0()}，=1，2，3，4，5，6；以表3种的4个参数作为比较数列，记为x={x()}，=1，2，3，4。即0为悬垂系数，1为透气率，2为透湿量，3为经向毛细效应，4为纬向毛细效应。

3.2 无量纲化

对不同单位或不同初值的参考数列和比较数列进行处理，使其无量纲化。本文对每一个数列的所有数据采用均值化处理，得到一个新的数列。

x()为第个参数第点的原始数据，为第个比较数列的原始序列的平均值，表示第个比较数列第点均值变化后的新数据。无量纲化后的新数据见表4所示。

表4 无量纲化后的新数据

3.3 求两级差

参考数列0与比较数列x在第k点的绝对值：

两级差数据见表5所示。

表5 两级差数据

对于一个参考数列0，有好几个比较数列1、2、3、4的情况，可用下述关系表示被比较数列与参考数列在各点（时刻）的差。

表6 动态关联系数

表6 动态关联系数

i=1i=2i=3i=4 k=10.840.601.000.98 k=20.640.560.740.67 k=30.570.440.480.39 k=40.520.360.390.37 k=50.821.000.790.65 k=61.000.750.711.00

表7 静态关联系数

表7 静态关联系数

i=1i=2i=3i=4 k=10.810.591.000.86 k=20.580.520.630.60 k=30.530.420.430.37 k=40.490.340.350.35 k=50.751.000.680.59 k=61.000.770.721.00

3.5 求取关联度r

所谓关联度是指参考数列对比较数列关联系数的均值，其计算公式如下：

式中是比较数列x对参考数列0的关联度。

织物的透气率、透湿量、经向毛细效应、纬向毛细效应与悬垂性能的关联度如表8所示。

表8 悬垂系数的关联度

按灰色关联分析原则，关联度大的对比数列与参考数列关联最为密切，反之疏远。根据表8可得出关联顺序为：动态悬垂系数：1＞3＞4＞2，即影响动态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量；静态悬垂系数：1＞3＞4＞2，即影响静态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量。

4 测试结果分析

从上述结果可知透气率对织物动态悬垂系数和静态悬垂系数影响比较大。这主要是因为织物的透气率取决于织物中空隙大小及多少。[8]在织物纤维性状、纱线性状、织物几何结构和后整理工艺等一定的情况下，织物空隙越大、越多，织物纱线间的相互作用力和单位面积重量也越小，织物越柔软，悬垂时能构成半径较小的波状屈曲，悬垂性较好。现就透气率与悬垂系数的相关性进行探讨。透气率与动态悬垂系数的关系如图1所示，透气率与静态悬垂系数的关系如图2所示。

图1 透气率与动态悬垂系数的关系

图2 透气率与静态悬垂系数的关系

由图1、图2可知，随着透气率的增加，织物的动态悬垂系数和静态悬垂系数均减小，将织物的透气率作为自变量，悬垂系数作为因变量，建立回归方程。透气率与动态悬垂系数的回归方程为：= -0.008+ 57.63，相关系数平方值为0.711，透气率与静态悬垂系数的回归方程为：= -0.008+ 59.36，相关系数平方值为0.693。透气率与悬垂系数之间的线性关系显著。

5 结论

（1）影响动态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量；

（2）影响静态悬垂系数的主次顺序为：透气率、经向毛细效应、纬向毛细效应和透湿量。

（3）透气率与悬垂系数之间的线性关系显著。

[1] 邓聚龙．灰理论基础[M]．武汉：华中科技大学出版社，2002．

[2] 汪学骞，朱浩，王宾．织物湿热舒适性能的测试与灰色评价[J]．纺织学报，1987，8（3）：37-39.

[3] 王健．织物悬垂性能与织物结构参数的灰色关联性[J]．棉纺织技术，2006，34（3）：19-21.

[4] 王瑄．电磁波屏蔽织物服用性能影响因素的灰色优势分析[J]．纺织学报，2009，30（8）：50-53.

[5] 马顺彬．竹浆/棉交织物力学性能的灰色聚类分析[J]．现代丝绸科学与技术，2011，26（3）：84-86．114．

[6] 刘海．灰色系统理论的茧丝绸价格指数分析与预测[D]．苏州：苏州大学，2012．

[7] 黄紫娟，王天晓，诸葛祥硕．毛织物悬垂性能与织物结构参数的灰色关联性[J]．现代丝绸科学与技术，2014，29（5）：174-176．

[8] 姜怀．纺织材料学[M]．北京：中国纺织出版社，1987．

Grey Correlation between Air Permeation Rate, RH Transmission Rate, Capillary Effect and Drape Coefficient

MA Shun-bin, CAI Yong-dong

(Jiangsu College of Engineering and Technology, NanTong Jiangsu 226007, China)

Six kinds of fabrics with different specification were designed and woven，air permeation rate，RH transmission rate，capillary effect and drape coefficient of fabrics were tested，then study their correlation by using grey system theory. The results show that: The primary and secondary sequence that influence dynamic drape coefficient were air permeation rate, warp capillary effect, weft capillary effect and RH transmission rate；The primary and secondary sequence that influence static drape coefficient were air permeation rate, warp capillary effect, weft capillary effect and RH transmission rate；the linear relationship between air permeation rate and drape coefficient was significant.

air permeation rate；RH transmission rate；capillary effect；drape coefficient；grey system theory

TS101.192

A

2095－414X(2016)06－0032－05

马顺彬（1978-），男，副教授，研究方向：纺织科学与工程.

江苏省先进纺织工程技术中心项目（苏政办发2014[22]号）；南通市新型纤维材料重点实验室（CP12014003）；江苏高校“青蓝工程”科技创新团队（苏教师[2014]23号）；江苏高等学校优秀科技创新团队（苏教科[2013]10号）.