超序半群上的正则超同余
2016-10-13李倩倩谢祥云
李倩倩,谢祥云
超序半群上的正则超同余
李倩倩1,谢祥云2
(1.连云港高级中学,江苏 连云港 222000;2.五邑大学 数学与计算科学学院,广东 江门 529020)
给出了超序半群上正则超同余的定义,并通过超序半群的超理想构造了一个正则超同余关系,解决了B.Davvaz等在《Relationship between ordered semihypergroups and ordered semigroups by using pseuoorders》一文提出的超序半群上正则超同余的存在性问题. 进一步地,探讨了正则超同余和拟序的关系.
超序半群;超同余;正则超同余;拟序
1 引言与预备知识
同余理论对序半群的结构研究起着很重要的作用[1-2],同样,在超序半群中,超同余理论具有同余理论在序半群中同等重要的地位[3-4]. 在一般的序半群中我们知道:若是序半群上的二元关系,且是同余,不一定是序半群,即使是序半群,我们也很难知道中的序和中的序有没有关系. 1995年,N. Kehayopulu等[5]给出了序半群上拟序的概念,并通过拟序在序半群上构造了一个同余使得商半群是序半群,但并没有探讨该同余关系与拟序之间有什么关系. 谢祥云[6]在2000年给出了序半群上正则同余和强正则同余的概念,后续又探讨了它们和拟序的关系以及它们的重要性质[7].
在超结构中,文献[8]给出了超序半群上拟序的概念,并通过拟序给出了超序半群的刻画,得出超序半群上存在一个超同余使商超半群是序半群,但没有解决“是不是存在超同余使得商超半群是超序半群”的问题. 本文在序半群(超序半群)同余理论的基础上给出了超序半群上正则超同余的定义,并对文献[9]提出的问题找出了一个超同余关系使商超半群是超序半群;进而研究了正则超同余与拟序的关系,并对正则超同余在超序半群中的作用进行了刻画.
定义1[8]210设是超序半群,是上的二元关系,称为上的拟序关系,如果满足以下条件:
定义2[8]210设和是两个超序半群,叫做超序半群到的同态,若满足以下条件:
2 正则超同余
命题1[4]159设是超序半群,是的超理想,如果上的Rees关系:或,则是上的超同余关系.
下面对文献[9]中提出的问题构造一个超同余关系使其商超半群是超序半群.
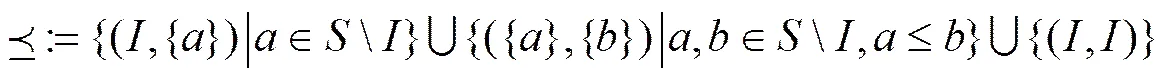
3 正则超同余和拟序
为了得到正则超同余和拟序之间的关系,引入下面的引理.

由引理1可得到正则超同余和拟序的关系.


所以有

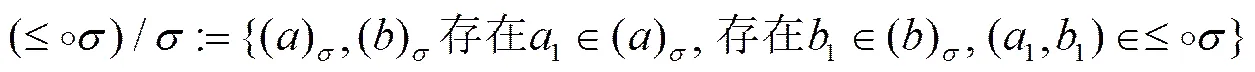



因而有:



参考文献:
[1] XIE Xiangyun. Contributions to theory of congruences on ordered semigroups [D]. Lanzhou: Lanzhou University, 1995.
[2] XIE Xiangyun. On congruences on ordered semigroups [J]. J Math & Res Expo, 2002, 21: 207-204.
[3] DAVVAZ B. Some results on congruences in semihypergroups [J]. Bull Malays Math Sci Soc, 2000, 23: 53-58.
[4]GAO Fei, XIE Xiangyun. Fuzzy rees hypercongruences on hypersemigroups [M]//ZENG Dehui. Applied Informatics and Communication. Shenzhen:Shenzhen University, 2011: 262-269.
[5] KEHAYOPULU N, TSINGELIS M. Pseudoorder in ordered semigroup [J]. Semigroup Forum, 1995, 50: 389-392.
[6] XIE Xiangyun. On regular, strongly regular congruences on ordered semigroup [J]. Semigroup Forum, 2000, 61: 159-178.
[7] XIE Xiangyun. Remarks on regular congruences on po-semigroup [J]. SEA Bull Math, 2000, 24: 661-666.
[8] DAVVAZ B, CORSINI P, CHANGPHAS L. Relationship between ordered semihypergroups and ordered semigroups by using pseuoorders [J]. European J Combinatorics, 2015, 44: 208-217.
[9] SEN M K, AMERI R, CHOWDHURY G. Fuzzy hypersemigroups [J]. Soft Comput, 2008, 12:891-900.
[责任编辑:熊玉涛]
On Regular Hypercongruences on Ordered Hypersemigroups
LIQian-qian1, XIEXiang-yun2
(1. Lianyungang Senior Middle School, Liyungang 222000, China;2. School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)
We introduce the concept of regular hypercongruences of ordered hypersemirgroups, and construct a regular hypercongruence on an ordered hypersemigroup in terms of hyperideals, which resolves an open existing problem of regular hypercongruences in “Relationship between ordered semihypergroups and ordered semigroups by using pseuoorders” by B.Davvaz, etc. Further, we discuss the relationships between regular hypercongruences and pseudoorders.
ordered hypersemirgroups; hypercongruence; regular hypercongruence; pseudoorders
1006-7302(2016)04-0009-07
O152. 7
A
2016-03-30
国家自然科学基金资助项目(11361027,11271040);广东省自然科学基金资助项目(2014A030313625);广东省教育厅省级重大项目(自然科学类)(2014KZDXM055).
李倩倩(1987—),女,安徽砀山人,在读硕士生,主要研究方向为半群的代数理论;谢祥云,教授,博士,硕士生导师,通信作者,研究方向为序半群的代数理论、模糊代数、粗糙集理论.
