关于一类混合型泛函积分方程最佳平方逼近方法的深层研究

2016-10-13王奇生王华生

五邑大学学报（自然科学版） 2016年4期

王奇生，王华生

王奇生，王华生

（五邑大学数学与计算科学学院，广东江门 529020）

通过对泛函积分方程最佳平方逼近解法的深层研究，解决了本文第一作者2014年在《Journal of Computational and Applied Mathematics》上发表的论文存在的两个不足，证明了一类带复合因子Volterra-Fredholm混合型积分方程解析解和最佳平方逼近解的存在唯一性定理.

Volterra-Fredholm型积分方程；复合因子；最佳平方逼近；解的存在唯一性

本文第一作者多年讲授研究生课程数值计算方法[1-2]，经常开展讨论班形式的研讨型教学方法的研究. 结合学科研究前沿，我们将Lagrange插值法[3]、Taylor多项式逼近方法[4]、最佳平方逼近方法[5]、不动点迭代方法[6]等经典数值计算方法成功运用于求解积分微分方程问题，并取得了一些研究成果. 本文是对文献[5]的进一步探究，得到了一些深层的结果.

文献[5]研究了一类带复合因子的Volterra-Fredholm混合型积分方程问题：

并利用最佳平方逼近方法解决了其数值求解问题，给出了最佳平方逼近解的求解格式及收敛性分析等结果，然而并没有对方程（1）解析解的存在唯一性及最佳平方逼近解的存在唯一性进行证明. 本文是对文献[5]的进一步研究，解决了上述两方面的不足.

1 解析解的存在唯一性定理

利用Banach不动点定理，给出方程（1）的解析解存在唯一性的充分条件.

定理1（解析解的存在唯一性）如果下述条件满足，即

则积分方程（1）存在唯一解.

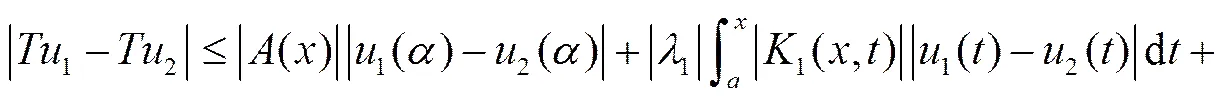
2 最佳平方逼近解的存在唯一性定理

对方程（1），定义算子

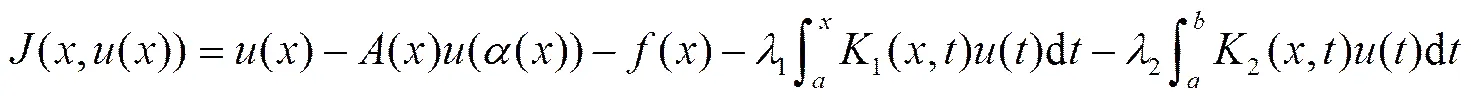
则

证明因为

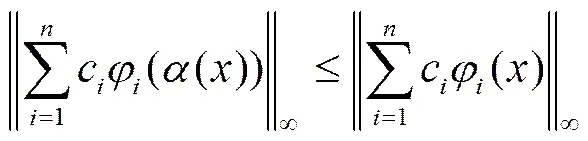
根据式（3）和式（8），有

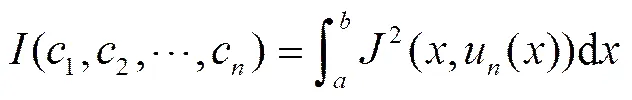
亦即

注意到方程组（13）可以写成如下矩阵形式：

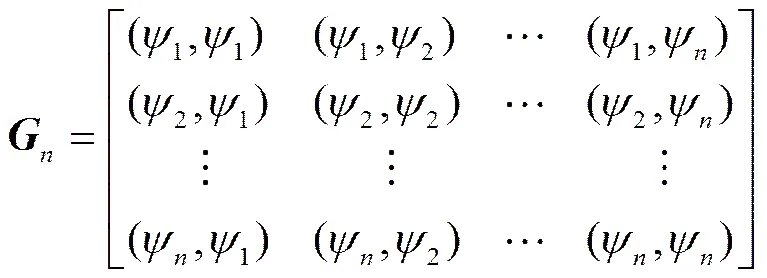
定理3（最佳平方逼近解的存在唯一性）如果方程（1）满足定理1中的条件，则方程（1）的最佳平方逼近解也是存在且唯一的.

证毕.

参考文献：

[1] 李庆扬，王能超，易大义. 数值分析[M]. 5版. 北京：清华大学出版社，2008.

[2] WAZWAZ A M. A first course in integral equations [M]. 2nd Edition. London: World Scientific, 2015.

[3] WANG Keyan, WANG Qisheng. Lagrange collocation method for solving Volterra-Fredholm integral equations [J]. Applied Mathematics and Computation, 2013, 219(21): 10434-10440.

[4] WANG Keyan, WANG Qisheng. Taylor polynomial method and error estimation for a kind of mixed Volterra- Fredholm integral equations [J]. Applied Mathematics and Computation, 2014, 229: 53-59.

[5] WANG Qisheng, WANG Keyan, CHEN Shaojun. Least squares approximation method for the solution of Volterra-Fredholm integral equations [J]. Journal of Computational and Applied Mathematics, 2014, 272(3): 141-147.

[6] WANG Keyan, WANG Qisheng, GUAN Kaizhong. Iterative method and convergence analysis for a kind of mixed nonlinear Volterra-Fredholm integral equation [J]. Applied Mathematics and Computation, 2013, 225(12): 631-637.

[责任编辑：熊玉涛]

An Exploration of the Best Square Approximation Method for a Kind of Mixed Functional Integral Equation

WANGQi-sheng, WANGHua-sheng

(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)

This paper is a deep study of the least squares approximation method for the functional integral equation, and solves the two deficiencies in a paper published by the first author of the paper in(2014). The proof of the existence and uniqueness theorem of the analytic solution and the optimal square approximation solution for a class of Volterra-Fredholm mixed type integral equations with complex factors is given.

Volterra-Fredholm integral equation; complex factors; best square approximation; existence and uniqueness

1006-7302（2016）04-0001-04

O189.1

2016-04-08

广东省自然科学基金资助项目（2015A030313643）；五邑大学学位与研究生教育改革研究项目（YJS- JGXM-14-02；YJS-JGXM-14-03）.

王奇生（1961—），男，湖南衡阳人，教授，博士，硕士生导师，研究方向为微积分方程数值解法.