逐步Ⅱ型截尾竞争失效产品的Marshall-Olkin扩展指数分布统计分析
2016-10-13贺兴时王慧敏
王 燕, 贺兴时,王慧敏
(西安工程大学 理学院,西安 710048)
逐步Ⅱ型截尾竞争失效产品的Marshall-Olkin扩展指数分布统计分析
王燕, 贺兴时,王慧敏
(西安工程大学 理学院,西安 710048)
为研究产品寿命服从Marshall-Olkin扩展指数分布的截尾寿命试验的统计特性,文中基于Marshall-Olkin扩展指数分布的逐步Ⅱ型截尾寿命试验竞争失效模型,对寿命参数的极大似然、渐进区间及Bootstrap区间进行了估计.利用Monte-Carlo模拟方法对逐步Ⅱ型截尾寿命试验竞争失效模型进行了仿真.结果表明在不同的截尾试验方案下,随着样本容量的增大,参数极大似然估计值越接近真值,在同一试验方案下,Bootstrap区间的覆盖率比渐进置信区间的更优.
Marshall-Olkin扩展指数分布;极大似然估计;渐进置信区间;Bootstrap区间
approximate confidence interval;Bootstrap confidence interval
指数分布是可靠性分析中常用的分布之一,但由于其分布的危险比率函数为常数,导致分布在实际应用中受到限制.为有效解决该问题,Marshall 和 Olkin于1997年提出了一种新的寿命分布,即Marshall-Olkin扩展指数分布[1](Marshall-Olkin extended exponential,MOEE),其原理是通过扩展已有的指数分布族来增加模型的灵活性,由此在可靠性统计分析中得到了广泛的应用.同时,随着Marshall-Olkin扩展指数分布理论研究的深入,大量的国外学者在该分布中开始探讨极大似然估计及贝叶斯估计,以进一步改进其性能.比如Rao和Ghitany[2-3]研究的该分布在可靠性测试计划及经济可靠性测试计划中的应用,并通过实例验证结果表明该分布优越于其他可靠性测试计划;Srivastava[4]利用蒙特卡洛方法,研究的MOEE的极大似然估计及贝叶斯估计;以及Narinder Pushkarna研究的在逐步Ⅱ型右删失模型下该分布的邦弗朗尼和基尼系数的递推关系[5].在我国,也有大量的统计学者们开始对该主题的研究,其研究热点主要分布在在MOEE分布的分布特征及参数估计方面,比如李国安[6]研究的多元Marshall-Olkin型指数分布的统计特征,并通过导出二元Marhsall-Olkin型指数分布的一个特征,得到了该分布的极大似然估计与距估计;同时,文献[7]研究了MOEE模型的性质及应用,并给出Marshall-Olkin二元指数分布模型的边际分布,以及文献[8]讨论了Marsall-Olkin Laplace(AMOL)分布的性质,得到了该分布的自回归模型的一个充要条件.
通过文献回顾,发现国内外学者对MOEE的研究,主要集中在MOEE分布的分布特征及参数估计方面,也得出了一些重要结论,对MOEE在截尾寿命试验统计分析的研究尚未深入探讨.为此,本文在逐步Ⅱ型截尾试验下,研究了Marshall-Olkin扩展指数分布的基本过程,并对寿命参数的极大似然、渐进区间及Bootstrap区间进行了估计,进而通过构建试验方案开展仿真试验研究.
1 模型构建
由于产品内部结构及外界工作环境的复杂性,导致产品失效的原因较多,任何一个原因的发生都有可能导致产品失效,称这类产品为竞争失效产品.引起产品失效的原因称为产品失效机理.在潜在的产品失效机理中,正确的判断导致产品在达到预期寿命之前失效的原因机理是产品质量评估的一个重要问题.现有文献通常采取寿命试验及工程判断等方法来识别失效机理对产品失效的敏感程度.在寿命试验的基础上,通过对产品失效数据进行分析,从而改进产品的设计和研制,进而提高产品的质量水平.
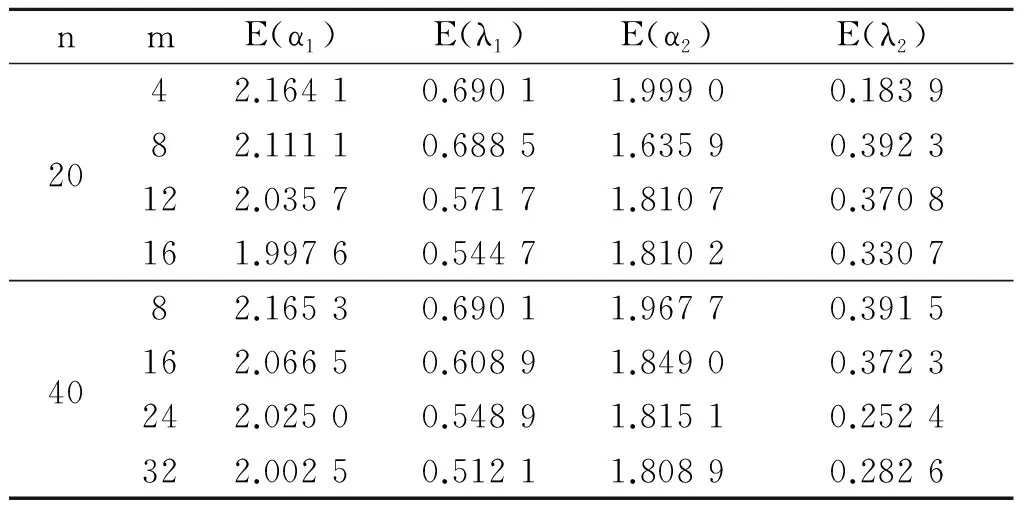
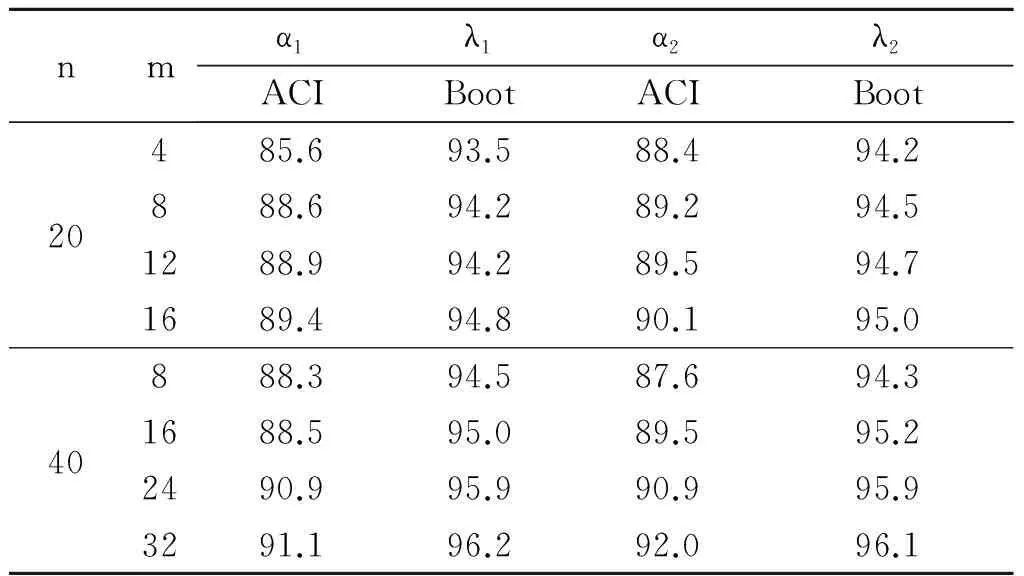
在逐步Ⅱ型截尾竞争失效产品的寿命试验中,假定有n个产品进行寿命试验,产品的失效机理有k个,且各失效机理发生时间Ti(i=1,2,…,k)相互独立.当第一个产品失效时,从未失效的n-1个产品中随机抽取R1个产品移离试验,并记录该产品失效时间为X1与引起失效的机理编号δi(i=1,…,k).直到第m(m 若Xi表示第i个失效机理发生的时间,则产品的寿命为T=min(X1,X2,…Xk),Xji(j=1,2,…,k;i=1,2,…,n)表示第个i产品失效机理j的发生时间. 现假定引起产品失效的机理有2个,记为{1,2}且相互独立,则所有的方法都可以推至k个失效机理. 设产品失效时间Xi(i=1,2,…,m)服从不同形状参数α1,α2和尺度参数λ1,λ2的Marshall-Olkin扩展指数分布,Xji服从形状参数为αj,尺度参数 λj的Marshall-Olkin扩展指数分布.由此,其概率密度函数、分布函数可分别表示为 (1) (2) 由式(2)可得,相应的生存函数可表示为 (3) 由式(3)可得,基于竞争失效模型产品的生存函数可构建为 (4) 逐步Ⅱ型截尾寿命试验下竞争失效产品数据为(t1,δ1),(t2,δ2),…,(tm,δm)则引起第i个产品失效的原因为δj,(δj=1,2),示性函数为Ij={i;δi=j}. 在逐步Ⅱ型截尾试验下,基于Marshall-Olkin扩展指数分布竞争失效产品数据为(t1,δ1),(t2,δ2),…,(tm,δm),得到产品寿命的似然方程为 (5) 其中C为常数. (6) 现对式(5)取对数,得到的对数似然函数可表示为 l=log(L(ti;λ,α))=n1logλ1+n2logλ2- (7) 同理,得到的似然方程可表示为 (8) (9) 由此,利用牛顿迭代法对式(8)和式(9)进行求解,从而得到极大似然估计. 3.1渐进置信区间估计 由于未知参数αj,λj,的精确分布难以得到,所以无法通过枢轴量法构造参数的精确区间估计.可利用极大似然估计的渐进正态性[10]与Fisher信息矩阵,构造未知参数αj,λj,的渐进置信区间. 具体而言,参数的Fisher信息矩阵为 则参数的方差协方差矩阵为 j=1,2 3.2Bootstrap区间 对近似区间方法而言,只有在大样本的前提下才具有明显优势.相反,在样本适量的情况下,Bootstrap方法[11-12]在构建参数置信区间方面更具优势.为此,Bootstrap方法的构建过程如下: 用Monte-Carlo模拟方法,得到未知参数(α1,α2,λ1,λ2)的极大似然估计及其区间估计,并在不同样本容量和实验方案下对比各种方法的优略性. 表1 截尾试验方案表 同时,基于1 000次Monte-Carlo模拟数据,计算置信水平为95%的区间覆盖率,得到的仿真结果见表3.其中,“ACI”,“Boot”分别表示渐进置信区间和Bootstrap区间. 由表2可见,在小样本下,极大似然估计的估计效果较差.但是,随着样本容量的增大,参数的极大似然估计值越接近参数真值.同时,在给定的定样本容量及试验方案下,与参数(α2,λ2)相比,参数(α1,λ1)的极大似然估计更稳定.原因在于当α1<α2<λ1<λ2时,产品失效机理1导致产品失效的概率要大于机理2. 表2 不同试验方案下的参数期望值 表3不同试验方案下参数区间覆盖率(%) Tab.3 The coverage percentages of the parameters in different schemes(%) nmα1λ1α2λ2ACIBootACIBoot485.693.588.494.220888.694.289.294.51288.994.289.594.71689.494.890.195.0888.394.587.694.3401688.595.089.595.22490.995.990.995.93291.196.292.096.1 由表3可见,当选取覆盖率为考核指标时,Bootstrap方法的估计效果要优于渐进方法.主要原因在于极大似然估计的近似区间是建立在近似方差协方差矩阵基础上的,只有在样本容量足够大时才具有良好的近似性.同时,渐进置信区间的覆盖率,随着样本容量的n增大而增加.具体表现在:当样本容量从n=20,r=4增加到n=40,r=32时,参数α1的区间覆盖率从85.6%上升至91.1%. 1) 在逐步Ⅱ型截尾寿命试验下,通过建立似然方程,给出未知参数的极大似然估计值;采用近似方法、Bootstrap方法建立参数的置信区间. 2) 在小样本下,极大似然估计的效果较差.随着样本容量的增大,参数的极大似然估计值越接近参数真值. 3) 选取覆盖率为考核指标时,Bootstrap方法的估计效果要优于渐进方法.主要原因在于极大似然估计的近似区间建立基础为近似方差协方差矩阵,样本容量足够大时才具有良好的近似性. [1]MARSHALL A W,OLKIN I.A New Method of Adding a Parameter to a Family of Distributions with Applications to the Exponential and Weibull Families[J].Biomertrika,1997,84:641. [2]SRINIVASA R G,GHITANY M E.Reliability Test Plans for Marshall-Olkin Extended Exponential Distribution[J].Applied Mathematical Sciences,2009,55(3): 2745. [3]SRINIVASA R G,GHITANY M E.An Economic Reliability Test Plan for Marshall-Olkin Extended Exponential Distribution[J].Applied Mathematical Sciences,2011,3(5):103. [4]SRIVASTAVA A K,KUMAR V,HAKKAK A A.Parameter Estimation of Marshall-Olkin Extended Exponential Distribution Using Markov Chain Monte Carlo Method for Informative Set of Priors [J].International Journal of Advances in Science and Technology,2011,2(4):76. [5]PUSHKARNA N,SARAN J,TIWARI R.Bonferroni and Gini Indices and Recurrence Relations for Moments of Progressive Type-II Right Censored Order Statistics from Marshall-Olkin Exponential Distribution[J].Journal of Statistical Theory and Applications,2013,12(3):306. [6]李国安.多元Marshall-Olkin型指数分布的特征及其参数估计[J].工程数学学报,2005,22(6):1055. LI Guoan.A Characterization of the Multivariate Marshall-Olkin Exponential Distribution and Its Parameter Estimation[J].Chinese Journal of Engineering Mathematics,2005,22(6):1055.(in Chinese) [7]周菊玲,梁晓佳.Marshall-olkin二元指数分布[J].新疆师范大学学报(自然科学版),2013,32(4):63. ZHOU Juling,LIANG Xiaojia.Marshall-Olkin Brivariate Exponential Distrbution[J].Journal of Xinjiang Normal University(Natural Sciences Edition),2013,32(4):63.(in Chinese) [8]颜荣芳,张娟.非对称Marshall-Olkin Laplace分布及其在自回归模型中的应用[J].应用概率统计,2010,26(3): 245. YAN Rongfang,ZHANG Juan.Asymmetric Marshall-Olkin Laplace Distribution and Its Application in Autoregressive Model[J].Chinese Journal of Applied Probability and Statistics,2010,26(3):245. (in Chinese) [9]SARHAN A M ,ALAMERI M ,AL-WASEL I .Analysis of Progressive Censoring Competing Risks Data with Binomial Removals[J].Journal of Mathematics Analysis,2008,2(20): 965. [10]茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004. MAO Shisong,CHENG Yiming,PU Xiaolong.Probability and Mathematical Statistics[M].Beijing:Higher Education Press,2004.(in Chinese) [11]EFRON B.Bootstrap methods: Another Look at the Jackknife[J].Annals of Statistics,1979,7(1):1. [12]PITUCH K A,STAPLETON L M.The Performance of Methods to Test Upper-Level Mediation in the Presence of Nonnormal Date [J].Multivariate Bechavioral Research,2008,43(2):237. (责任编辑、校对张立新) Statistical Analysis of Competing Failure Models with Marshall-Olkin Extended Exponential Distribution under Progressive Type Ⅱ Censored WANGYan,HEXingshi,WANGHuimin (School of Science,Xi’an Polytechnic University,Xi’an 710048,China) In order to study the statistical properties of the competing risk model based on the Marshall-Olkin extended exponential distribution under the censoring test,the maximum likelihood estimates,the approximate and the Bootstrap confidence intervals of the parameters were derived based on the competing risk model under the progressive type II censored.Then,one data set was used for illustrative purpose in conclusion by the monte carlo method.Simulation results show that,with the increase of the sample size,the maximum likelihood estimates of the parameter are closer to the true values.Under the same test scheme,the bootstrap interval coverage is superior to the asymptotic confidence interval coverage. Marshall-Olkin extended exponential distribution;maximum likelihood estimate; 10.16185/j.jxatu.edu.cn.2016.07.001 2016-04-20 陕西省科技厅软科学基金(2014KRM28-01);陕西省教育厅自然科学基金(12JK0744,11JK0188) 王燕(1987-),女,西安工程大学助教,西北工业大学博士研究生,主要研究方向为可靠性统计分析. E-mail:wywzyf@126.com. 中图号:O213.2A 1673-9965(2016)07-0517-05
2 极大似然估计
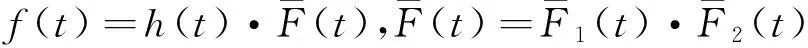




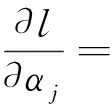
3 参数区间估计
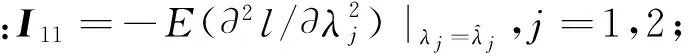

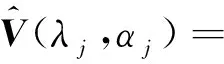
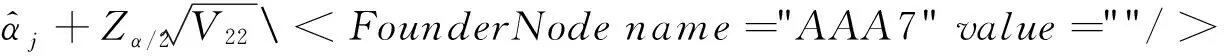
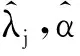
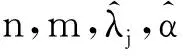

4 算例验证
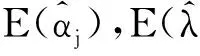

5 结 论
