聚类分析方法在法官员额配置的运用探索

许舜娟

厦门市湖里区人民法院，福建　厦门　361006



聚类分析方法在法官员额配置的运用探索

许舜娟

厦门市湖里区人民法院，福建厦门361006

员额制是实现法官检察官专业化、职业化的重要基础制度，是实行司法责任制的前提。中央确定的以省为单位、以政法专项编制为基数的39%的员额比例，但这不是一个恒定的比例，应当根据三级法院的审级职能，以及不同区域法院的实际情况，进行适当的调整。为此，本文尝试从统计学的角度出发，将多元统计分析方法中的聚类分析方法引入法官员额配置之中，希望对司法改革中的法官员额制有所帮助，以期为决策层优化法官人力资源配置提供有益参考。

聚类分析；法官员额；比例配置

一、影响法官员额比例设置的因素分析

“四五改革纲要”将确定法官员额制度的因素分为两类：一是法院辖区经济社会发展状况、人口数量(含暂住人口)、案件数量、案件类型等基础客观数据，可以通过现有资料合理预测未来一定时期的变化情况；二是需要结合考虑的因素，包括法院审级职能、法官工作量、审判辅助人员配置、办案保障条件等涉及相关司法体制配套改革，与法官员额制度一样是本轮司法改革的重要事项。市场经济越发达，交往方式越复杂，则矛盾纠纷越多。在一般情况下，社会的法治化程度越高、经济文化越发达，往往案件数量越多、新类型案件、复杂、疑难案件、大标的案件会比较多，而案件的增长幅度也往往与GDP增长幅度相吻合。

人是一切社会关系的总和。随着人们交往的开始和深入，矛盾、对抗、争议、纠纷便产生了，当双方不能通过协议解决问题时，诉讼便产生了。从一般情况讲，法院辖区人口数量越多，纠纷越多，诉讼到法院的案件也越多。

法官的主要工作就是审理案件，从某种意义上说，案件数量与法官人数的关系更为直接，在确定法官员额时必须以案件数量为参考依据之一。若不考虑其他因素，法官工作量的直接量化形式就是案件的数量。

二、确定法官员额比例

省高院在全省39%员额比例配置范围内，具体确定辖区各级法院的员额比例，以便于平衡各法院之间的地区差异和审级差异。根据三级法院功能定位、任务安排和实际情况，在三类人员各自员额总额度内，对各级法院员额比例结构进行适当调整。

(一)聚类分析方法的提出及作用

每个法院法官员额比例设置，可以考虑以不同层级法院为基础，设置不同的比例，同时在基准比例上设置浮动区间。每个法院的法官员额比例只能在基准比例的浮动区间内取值，不得超出区间值。对中级人民法院乃至众多的基层人民法院，一方面可以由各个法院根据自身实际情况得出一个初步法官员额比例值，通过这种方法得出的法官员额比例数据具备相当的合理性与参考价值，但该方法没有解决各个比例值之间可比性差这一核心难题，也缺乏统一的理论依据，不同法院所采用的法官员额方案可能也存在相当的差异，从而使得该方法在精确度和权威性上终究无法让人完全满意。为解决该方法不足，可以将每个法院作为一个样本进行统计分析，把指导性意见已明确的辖区人口、案件数量和经济发展水平等几个考量法官员额的关键性参考因素，作为每个样本的随机变量。各变量之间虽然不同质，但存在一定关联性，将各个变量割裂开来进行单独分析，不仅会丢失信息，也不容易取得好的研究成果。可以考虑采用多元统计分析方法中的聚类分析方法对不同的法院样本对象进行科学的分类，并加以综合分析，以提高分析及管理效率。聚类分析方法对样本数据函数的分布无特定要求，可以在一定能够程度上可以消减不同样本对象间数据的可比性差异，同时通过对数据的标准化处理，消除不同数据间量纲的影响。通过聚类分析方法，可以将相关影响因素综合起来进行分析，找出属于同一层次的样本对象，将样本进行合理归类，从而实现对样本对象的整体管理而非逐个的分散管理。

(二)实证：聚类分析方法在法官员额配置中的应用示例

以某市法院为样本对象的聚类分析。现拟对某市A、B、C、D、E、F六个基层法院的法官员额配置进行分类，具体步骤如下：

1.选定数据

选择考量法官员额的关键性参考因素，假设选定指导性意见已明确的辖区人口、案件数量和经济发展水平这3个要素，并以GDP总值作为衡量辖区经济发展水平的参考指标。①2015年，这六个法院所在辖区的人口分别为99.1、101.5、64.4、33.2、54.4、33.4(计量单位略，下同)；案件数量分别为3.30、1.59、0.87、0.73、1.01、0.68；GDP总值分别为1056.08、778.14、494.15、511.70、245.32、380.62。

2.标准化处理

为消除不同数据间量纲(计量单位及方向等)的影响，在进行分类前必须先将选定的数据进行标准化处理，②并将标准化后的计算结果加总，作为该样本用以聚类分析的数据值。根据上述办法进行处理，得到

六个法院标准化后加总的数值分别为5.15、2.34、-0.85、-2.06、-1.99、-2.60。

3.分类划分

距离值越小，代表两个样本接近程度越大；反之，距离值越大，代表两个样本接近程度越小。从而根据实际需要，将距离相对接近的样本归为一类。将标准化后的6项数值进行两两相减，得出原始距离阵为：

ABCDEFA02.8167.217.147.75B-2.8103.194.44.334.94C-6-3.1901.211.141.75D-7.21-4.4-1.210-0.070.54E-7.14-4.33-1.140.0700.61F-7.75-4.94-1.75-0.54-0.610

找出距离阵中非对角线上绝对值最小的距离值为0.07，将该最小距离值所对应的D、E两个样本合并，并重新计算新的距离阵。③通过反复进行新的距离计算及归类合并，根据管理需要，可将这6个法院分为N类(N<6)。假设分为两类，则最终所得结果为：

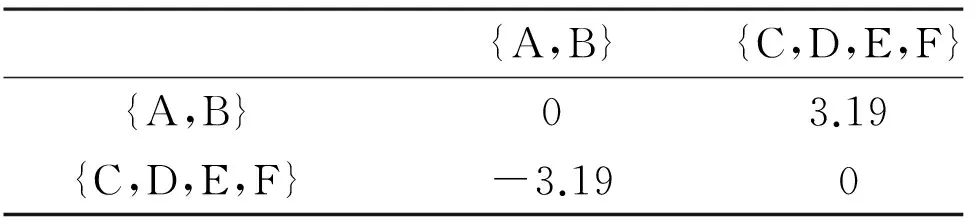
{A,B}{C,D,E,F}{A,B}03.19{C,D,E,F}-3.190

计算结果表明，A、B两个法院属于同一个层次，C、D、E、F四个法院层次相当，且法官员额方面来说，这四个法院的员额比例可以低于前两个法院，其差距在一定意义上可以认为就是3.19。当然，由于各个法院承办法官及案件的具体情况不同，该分析结果只不过是一个初步的参考，尚需结合其他因素综合考虑，但该方法仍为法院法官员额比例配置提供科学、可靠的参考依据。

[注释]

①为简化聚类分析过程，便于直观理解，示例中选取了3个关键性的参考要素，实践中可以根据需要选取更多的要素项目，一并进行分析.

②标准化处理：先计算各数据的均值，并将各项数据值减去该均值再除以各项数据的标准差，再根据是否评价方向是否相反，考虑是否对反向评价的数据取负值.

③聚类分析方法中，定义合并后的新类与其他样本间距离的方法有很多种，如最短距离法、最远距离法、中间距离法等，本文采用最短距离法，即将合并为一类的样本中，与其他样本距离最小的值作为合并后该类与其他样本间的距离.

D926.2

A

2095-4379-(2016)28-0136-02

许舜娟(1982-)，女，福建东山人，管理学硕士，福建省厦门市湖里区人民法院。