极小通讯延迟的虚拟机分配算法*
2016-10-12高任飞武继刚张耀国
高任飞,武继刚,周 莹,张耀国
1.天津工业大学 计算机科学与软件学院,天津 300387 2.广东工业大学 计算机科学与技术学院,广州 510006
极小通讯延迟的虚拟机分配算法*
高任飞1,武继刚2+,周莹1,张耀国1
1.天津工业大学 计算机科学与软件学院,天津 300387 2.广东工业大学 计算机科学与技术学院,广州 510006
GAO Renfei,WU Jigang,ZHOU Ying,et al.Virtual machine assignment for minimizing data latency.Journal of Frontiers of Computer Science and Technology,2016,10(7):924-935.
在现代基于虚拟化的数据中心上,虚拟机分配是实现云中资源有效调度的首要考虑。在云系统中,大数据被划分成多个数据存储在数据中心的数据结点上等待虚拟机处理,此时不仅存在虚拟机处理数据时的通讯延迟,也存在汇总计算结果时虚拟机之间的通讯延迟。虚拟机分配策略的不同将导致最大通讯延迟的不同。已经证明对数据结点分配虚拟机,并考虑虚拟机之间的通讯延迟,使得最大通讯延迟最小的问题是NP-hard问题。提出了一种新的虚拟机分配算法。该算法首先判断在通讯延迟的某一阈值内是否存在规模多于数据结点的能够互相通讯的虚拟机机群。若存在则用有效的回溯法寻找在此阈值下由虚拟机构成的完全子图,然后采用Hopcroft-Karp算法将完全子图中的虚拟机分配给数据结点。这种方法能够有效减小解空间,降低虚拟机分配的时间。实验结果表明,所提算法在Tree、VL2、Fat-Tree和BCube网络结构中,与当前最新的近似算法相比,平均情况下最大通讯延迟分别降低了10.39%、5.68%、9.09%、5.45%。
数据中心;虚拟机分配;通讯延迟;完全子图
1 引言
随着越来越多的数据密集型应用程序移动到云中去处理,大数据的处理成为人们普遍关心的重要问题之一[1-2]。像MapReduce/Hadoop(http://hadoop. apache.org)等处理框架对于执行这些密集型应用程序非常适用和高效[3]。云计算是基于虚拟化技术并且通过网络以按需付费方式获取计算资源(如存储资源、服务器资源等)的一种计算模式。用户可以按需租用云来处理大数据,如亚马逊EC2(http://aws.amazon. com/ec2/)和Cisco数据中心(http://goo.gl/Sil548)。虚拟化技术已经被证明是数据中心内一种实现资源共享的有效技术。然而对于云提供商而言,如何实现资源的有效管理仍然是面临的主要挑战[4]。虚拟机指通过软件模拟的具有完整硬件系统功能的、运行在一个隔离环境中的完整计算机系统[5]。在现代基于虚拟化的数据中心上,虚拟机分配是实现云中资源有效调度的首要考虑[6]。客户可以向云系统请求计算资源,如内存、硬盘、处理器等,云提供商则根据客户的请求情况进一步决定如何分配虚拟机,也就是虚拟机分配问题。有效的分配策略不仅可以减少通讯延迟,降低网络带宽消耗,也可以提高资源的利用率[7]。
当一个任务中的大数据被划分后,降低数据的总处理时间成为人们的主要目标。若对最大通讯延迟没有限制,总处理时间就会被延迟[8]。当出现任务或虚拟机负载不平衡,处理器较慢,网络堵塞时,一个任务的完成时间就会被延长。目前有许多的方法来处理这些问题。有些工作会注重网络代价和物理机代价的均衡问题[4],有些则注重虚拟机的调度问题[9]等。由于虚拟机的固有属性,虚拟机处理数据的时间不易被改变,但可以通过合理的虚拟机分配来降低虚拟机处理数据的通讯延迟。理想情况是使每个数据结点被本地虚拟机处理,这样数据结点和虚拟机之间的通讯延迟为零。然而,由于服务器容量有限,移动数据或虚拟机的代价较大等限制,把虚拟机移动到存储数据的服务器上,或者把数据移动到放置虚拟机的服务器中来使数据被本地虚拟机处理都是不现实的[4]。
然而,仅考虑使用距离数据结点较近的虚拟机来处理数据达到降低最大通讯延迟的目的是不充分的,因为虚拟机之间也需要通讯,比如在MapReduce云应用中,对最后的结果进行汇总就需要虚拟机之间通讯[3]。把一个大数据假设为一个团队,划分后的数据为团队中的成员,每个成员拥有一个虚拟机用来处理数据,团队中成员需要互相通讯,这才是团队合作[4]。最大通讯延迟不仅取决于数据与(处理此数据的)虚拟机之间的通讯延迟,也取决于(用来处理数据的)虚拟机之间的通讯延迟。为数据分配虚拟机并使最大通讯延迟最小的问题为NP-hard问题[8]。
文献[1]考虑了数据结点与虚拟机之间的通讯延迟,针对通讯延迟列出了4种目标,并分别给出每种目标下的虚拟机分配方法;文献[1]还考虑了虚拟机之间的通讯延迟,证明了此虚拟机分配问题的NP-hard性,提出了启发式算法,用贪心算法为数据结点寻找虚拟机的候选团,并结合匈牙利算法,数据结点分配虚拟机。文中使用贪心算法寻找虚拟机的极大团而非最大团,降低了为数据结点匹配虚拟机的可能性和容错性能。文献[8]在考虑虚拟机之间通讯延迟的基础上,概括了虚拟机分配问题的数学模型,通过改变原问题的约束条件将其转换成为近似问题,然后松弛成线性规划问题,并借用线性规划解法器来求解,其解空间仍为原问题的解空间。该近似算法阈值取自升序排列后的边的权值,存在相同阈值下重复处理的问题。
在数据中心内可利用的虚拟机数目多于数据结点,并且要求处理数据结点的虚拟机互相通讯,如此对虚拟机之间通讯的要求比较严格。因为虚拟机之间两两通讯,所以虚拟机之间的通讯模型所构成的图是一个完全图。在完全图中,每一对不同顶点都有一条边相连。在一定阈值下将完全图中大于阈值的边删除后所得到的图则不是一个完全图(阈值不为图中最大边的权值),此时存在简单图中最大完全子图的寻找问题,此问题仍是NP-hard问题[10]。最大完全子图(也称为最大团[11])是一个完全子图,并且不包含其他任何一个完全子图[12]。
本文从降低解空间的角度出发,提出了一种新的虚拟机分配策略:首先,设定阈值并根据阈值对图进行变换,在变换后的图中判断在此阈值内是否存在规模多于数据结点的能够互相通讯的虚拟机。若存在,则用回溯法递归地在解空间中搜索,并且在搜索过程中利用剪枝函数剪去无用的搜索来有效地寻找此阈值下的完全子图。若完全子图中虚拟机的规模不小于数据结点数目,将用Hopcroft-Karp算法为数据结点分配规模大于数据结点的完全子图中的虚拟机。因为完全子图中的虚拟机之间互相通讯已经符合不超过阈值的要求,所以下一步要解决的问题就是能否找到由(完全子图中的)虚拟机和数据结点构成的二分图在此阈值下的完备匹配。本文使用Hopcroft-Karp算法来解决此二分图的匹配问题。
这种虚拟机分配方法能够有效减小解空间,提高解的质量,并且降低虚拟机的分配时间。同时,进行大量实验,通过与文献[1]中的启发式算法和文献[8]中的近似算法进行比较来评估本文算法的性能和效率。文献[1]中的实验在一种分层的网络结构上进行,本文算法与之相比,在区间[1,64]、[1,256]和[1, 1 024]上最大通讯延迟相同,但运行时间平均改进了7.49%。在文献[8]的4种网络拓扑结构中两种近似算法所得到的最大通讯延迟相同,本文算法在Tree、VL2、Fat-Tree和BCube 4种网络结构中与当前最新的近似算法相对比,平均情况下最大通讯延迟分别降低了10.39%、5.68%、9.09%和5.45%。
2 虚拟机分配的问题描述
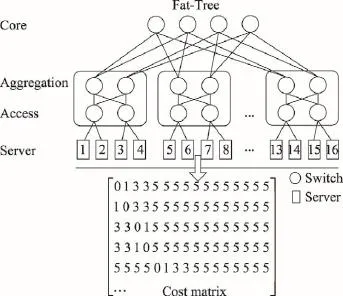
Fig.1 Network topology and corresponding cost matrix for Fat-Tree图1 Fat-Tree的网络拓扑结构及其代价矩阵
当前数据中心的拓扑结构通常为3层架构,例如Fat-Tree、VL2和Tree,这种3层架构遵循了一般的网络结构并给予了扩展(Cisco data center infrastructure 2.5)。如图1所示,结构中的底层为接入层,接入层的交换机连接服务器,顶层为核心层,汇聚层连接核心层和接入层,数据中心内的数据结点(data node,DN)和计算结点分布在底层的服务器中,数据结点用来存放数据,而计算结点用来处理数据,并由许多可利用的虚拟机(virtual machine,VM)构成。用户将待处理的数据存储在数据中心的DN上,并请求一定数目的VM进行处理。图1中矩阵表示Fat-Tree结构中两个服务器之间进行通讯所经过的交换机数目。例如,第一行中前3位数0 1 3的含义为:第一个服务器内的虚拟机与数据结点通讯不经过交换机;而位于第一个服务器中的虚拟机访问第二个服务器中的数据结点则经过1个交换机;当第一个服务器中的虚拟机访问第三个服务器中的数据结点时经过3个交换机。
本文使用如下实例来导出虚拟机分配问题。如图2所示,一个大数据在数据中心内被划成3块,分别存储在DN1、DN2和DN3这3个数据结点上,需要3个虚拟机来处理。现有5个可利用的虚拟机,它们分布在不同服务器上,任意一个虚拟机都可以处理任意一个数据结点,但通讯延迟各不相同,任意两个虚拟机之间通讯延迟也不相同。

Fig.2 3DNs,5 VMs and corresponding access latencies图2 3个DN与5个VM及其通讯延迟
图3是两种虚拟机分配方式。图3(a)表示第1、2、3个数据结点分别用第1、2、5个虚拟机处理,此时最大的通讯延迟是28。图3(b)表示第1、2、3个数据结点分别用第5、2、4个虚拟机处理,最大的通讯延是19。因此,VM的分配方式不同,最大的通讯延迟也不相同。若对最大通讯延迟没有限制,总处理时间则会被延迟。因此,需要制定一种虚拟机分配策略,使最大的通讯延迟最小。
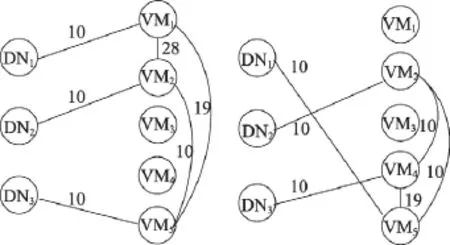
Fig.3 Two kinds of VMs assignments图3 两种虚拟机分配方式
本文遵循已有研究中的基本假设:
(1)一个VM处理一个DN。若一个DN需要k(k>1)个VM进行处理,则把DN复制k-1份存储在另外k-1个DN上[8]。
(2)通讯延迟满足三角不等式。两个结点间的通讯延迟由它们通讯所经过的交换机数目支配[7,13-15]。在数据中心的许多网络结构中,如Fat-Tree、VL2和Tree等[7],交换机数目遵循三角不等式原则,因此假设一个数据中心内通讯延迟满足三角不等式是合理的[1,16]。
给定一个图G=(D∪V,E1∪E2),D表示数据中心内数据结点的集合,V表示数据中心内可利用的虚拟机的集合。设eij∈E1(i∈D,j∈V)为连接DN与VM的边,e′ij∈E2(i,j∈V)为连接虚拟机与虚拟机之间的边。设dij∈R+(R+为正实数域)(i∈D,j∈V)为DN与VM之间的通讯延迟,d′ij∈R+(i,j∈V)为两个虚拟机之间的通讯延迟。目标是使最大通讯延迟最小。
定义1最大通讯延迟是指数据结点与虚拟机之间,以及处理数据结点的虚拟机与虚拟机之间所有通讯延迟的最大者,记作d,即


此时5个虚拟机之间互相通讯的延迟为:

因为最大通讯延迟比每一个DN与处理此DN的VM之间的通讯延迟大,所以有:

对于每个数据结点,必存在一个虚拟机来处理,而对于每个虚拟机,它可以处理数据结点,也可以不处理数据结点,即每个VM至多分配给一个DN,所以有:

因为加入了对虚拟机之间的通讯延迟的考虑,所以最大通讯延迟也要大于处理DN的虚拟机之间的通讯延迟,即:

为数据结点分配虚拟机的问题,即虚拟机分配(virtual machine assignment,VMA)问题,可以被归纳为如下混合整数规划问题[8]。

3 虚拟机分配算法
3.1算法思想及算法框架
若不考虑虚拟机之间的通讯,DN与VM之间通讯构成的图为二分图,对于二分图的匹配问题,已经有许多经典算法来解决,但是仅仅实现二分图的最优匹配是不够的,这对VM之间的通讯延迟没有界限控制。虚拟机之间互相通讯意味着任意两个VM之间存在通讯延迟,即VM之间通讯所抽象出的模型是无向完全图,在此完全图中每个顶点的度数都相同,都为|V|-1。要使最大通讯延迟最小,则要求被分配的虚拟机之间的通讯延迟都不能过大。
若通讯延迟能控制在一定阈值之内,在此阈值下能互相通讯的虚拟机的数目多于DN的数目,即互相通讯的虚拟机规模足够处理数据结点,就可以进一步为数据结点分配这些虚拟机,称此阈值下虚拟机规模满足数据结点。令Z为图G中边的权值所组成的集合,因为集合中元素具有无序性和互异性,所以集合Z的规模为G中边的种类数。对G中所有的边E1与E2进行遍历,在遍历过程中,出现不同的边的权值就记录在集合Z中。然后使用归并排序对Z中元素升序排列,设最大边的权值为Max。
给定一个图G1=(V,E2),G1⊂G,设阈值为t(t∈Z)。通过删除大于阈值t的边,将完全图G1转换为G1′,在G1′的完全子图内的虚拟机之间互相通讯,其通讯延迟肯定不超过t。具体转换为:先将G1复制给G1′,再将图G1′中不大于t的边的权值设为1(将边的权值设为1不影响完全子图的寻找,并且可以避免通讯延迟为0在二分图匹配时被当作无边处理的情况发生),大于t的边的权值设为0,相当于只保留G1′中权值不大于t的边。当t为Max时,G1中所有的边都会被保留,G1′仍然是一个完全图,其最大完全子图为|V|阶完全子图;当t小于Max时,转换后的G1′不再是一个完全图。要使最大通讯延迟不超过t,只能将完全子图中的虚拟机分配给数据结点。
首先根据图中所有边的权值确定阈值的取值集合Z,将Z中元素升序排列后依次设为阈值;其次在不同阈值下寻找合适的最大完全子图,若最大完全子图中VM规模不小于DN的规模,则在此阈值下为DN分配完全子图中的虚拟机,否则在此阈值下无解,继续增大阈值寻找合适的最大完全子图。直到完全子图中的VM规模满足DN,并且在此阈值下所有的DN都被匹配。本文提出的虚拟机分配算法(NEW-VMA)可形式化描述如下:
Algorithm NEW-VMA
Input:A graphG=(D∪V,E1∪E2)with weightsd′abanddabassociated with alle′ab∈E2and eab∈E1
begin
用Z记录E1与E2中边的不同权值,对Z中元素升序排列后并从1开始顺序标记;
fori←1 to|Z|do
t←the value of thei-th element inZ;
G1′←G1;
for each pair of edgesa∈Vandb∈Vdo
ifd′ab≤ tanda≠bthend′ab←1 inG1′;
elsed′ab←0 inG1′;
end if
end for
ift=Maxthen
The maximum access latency isMax;
else if DFC找到规模多于数据结点的由虚拟机构成的完全子图
Call BipartMatch to find the match;
if the number of matched DNs=|D|
break;
end if
end if
end if
end for
end
其中子过程DFC为寻找合适的完全子图过程,将在3.2节详细描述,子过程BipartMatch为二分图匹配过程,此二分图由数据结点与完全子图中的虚拟机构成的,将在3.3节描述。
3.2寻找合适的完全子图
若阈值t取值过小,则最大完全子图的规模过小,不足以处理DN;若t取值过大,虽然可以使最大完全子图中的VM规模满足DN,但是最大通讯延迟也伴随增大。本文提出的寻找合适的完全子图方法如下:
(1)在设定阈值后,根据图G1′中顶点的度数和边数以及相关定理判断是否存在规模多于数据结点的虚拟机的完全子图。
(2)根据判断结果决定是否寻找完全子图。若G1′中存在规模大于数据结点的虚拟机的完全子图,则用有效的回溯法寻找完全子图。
在图论中,存在这样的定理,即使不知道一个简单图中顶点之间的具体连接情况,根据图中边数也可以判断出图中至少存在多少阶的完全子图。
图兰(Turán)定理[17]:对于n个顶点的简单图,若图中边数l>M(n,p),那么它必包含 p阶完全子图。
由图兰定理可知,当n个顶点的简单图中的边数达到M(n,p)时,此图中一定存在p阶完全子图。设l 为G1′中的边数,可以根据l判断G1′中是否存在规模大于数据结点的虚拟机的完全子图。若存在,则进一步寻找完全子图。根据图兰定理可以判断当l>M(n,p)时,一定存在 p阶完全图。但是当l≤M(n,p)时,p阶完全图则不一定不存在。然而,可以知道,当度数不小于p-1的顶点数少于p时,p阶完全子图是一定不存在的。因为若存在p阶完全子图,则至少存在p个度数大于p-1的顶点。若度数大于或等于p-1的顶点数不少于p,则有可能存在p阶完全子图,即:


Procedure DFC/*Detect-and-Find-the-Clique*/
Input:AgraphG1′with weightsd′ij(i,j∈V)
begin
Calculate linG1′;
ifl>M(||V,||D)then
Call MaxClique to find the clique;
else
Calculatesjof each node inG1′;
Continue;
else
Call MaxClique to find the clique;
if the number of VMs in the clique<||Dthen
Continue;
end if
end if
end if
end
本文举例说明判断虚拟机的完全子图规模的过程。如图4是图2中5个虚拟机之间互相通讯的图。图中边的权值种类构成了集合Z={10,19,36,28},当t=10时,转换后的G1′如图5(a),度数大于2的顶点只有一个,则一定不存在一个三阶完全子图。因此t=10时,最大完全子图中的虚拟机规模小于数据结点规模。于是增大t,当t=19时,转换后的G1′如图5(b),图中边数l=8。根据图兰定理,若5个顶点的图中边数多于M(5,3)时,则一定存在三阶完全子图。因为 l>M(5,3)(此时 p=3,r=5%(p-1)=1,M(5,3)=5.25),满足图兰定理,所以当t=19时G1′中一定存在三阶完全子图。可调用MaxClique寻找完全子图。

Fig.4 Complete graph made by VMs图4 VM构成的完全图

Fig.5 Complete graph after transforming图5 转换后的完全图
子过程MaxClique是用回溯法在G1′中寻找完全子图的过程。访问到图G1′中某个顶点时,当该顶点违反问题的约束条件时,就不再访问其子孙,而回溯到它的父结点,选取下一个儿子为访问对象。在寻找虚拟机的最大完全子图过程中,设置剪枝函数F=Cn+n-k(Cn为当前团的顶点数,初始值为0,n为图中顶点数,k为结点层数),即当遍历到该顶点时,若当前完全子图的顶点个数与剩下还未遍历的顶点数之和小于记录中最大团的顶点数,则可剪枝,无需再进一步搜索子树。
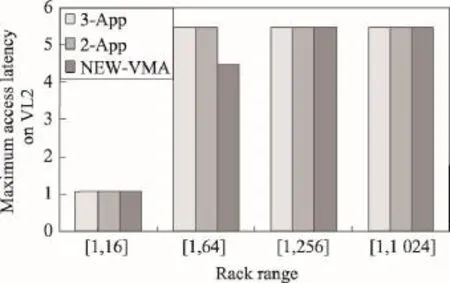
若数据中心内有n个虚拟机,则把寻找最大完全子图问题的解表示成n维向量(x1,x2,…,xn)作为解向量,xi对应于第i个虚拟机(顶点的标号与虚拟机的标号相同),其中xi取自有限集合Xi,Xi={0,1}(xi取1表示xi对应的顶点即第i个虚拟机在完全子图内,xi取0表示第i个顶点不在完全子图中),i=1,2,…,n。结点(x1,x2,…,xk)的含义为:已经检索k个顶点,其中xi=1对应的顶点在当前的完全子图内。用逻辑状态树Pn(x1,x2,…,xn)表达解向量应满足的性质,即约束条件,表示任意两个xi取1对应的顶点都有边相连。用Pk(x1,x2,…,xk)表示部分性质(k 用回溯法寻找最大完全子图的约束条件是遍历的顶点与当前完全子图内每个顶点都有边相连。在搜索过程中利用剪枝函数F剪去无用的搜索,抛弃不可能导致合法解的候选解,从而使求解时间大大缩短。设当前图中已经检索到的极大完全子图的顶点数为界B,代价函数F=Cn+n-k为目前的完全子图扩张为极大完全子图的顶点数的上界。当遍历该结点时,若该结点的代价函数值不超过B,则回溯,超过B,则进行下一步深度优先搜索。回溯法以深度优先策略遍历解空间树,递归地在解空间中搜索,并且在搜索过程中利用剪枝函数剪去无用的搜索,直到回溯到根结点。 通过在图5(b)中使用有效的回溯法寻找合适的完全子图来对算法的执行过程进行说明,如图6所示的寻找完全子图的状态树。 Fig.6 State-tree of finding complete subgraph图6 寻找完全子图的状态树 从解空间树的根结点开始,分枝规定左子树为1,右子树为0。遍历结点1,P1(1)成立,深度搜索至结点2处,此时P2(1,1)不成立,即结点1和结点2无边相连,则回溯至结点1处进入右子树搜索。结点3与当前团内顶点无边相连,P3(1,0,1)不成立,因此回溯并且遍历结点4,此时,P4(1,0,0,1)成立,结点4满足约束条件;继续深度搜索至叶结点,P5(1,0,0,1,1)成立,如图6中标记a处,此时得到第一个极大完全子图{1, 4,5},顶点数为3,界B为3。在状态树中结点b处,代价函数F=2 3.3二分图匹配 本节介绍虚拟机分配算法NEW-VMA中使用的子过程BipartMatch。该过程是用Hopcroft-Karp算法[18]为数据结点匹配最大完全子图中的虚拟机,此时最大完全子图中的虚拟机之间互相通讯已不超过设定阈值,因此为数据结点分配完全子图中的虚拟机时可以不考虑虚拟机之间的通讯问题。 为数据结点分配完全子图中虚拟机的问题为二分图匹配问题。本文二分图G2=(D∪P|v|,E1),G2⊂G,P|v|∈V,D与P|v|是两个不相交的子集,D是数据结点的集合,P|v|是为数据结点分配的完全子图中的虚拟机。M∈E1,若M满足当中任意两条边都不依附于同一个顶点,则称M是一个匹配。当图中某一子集中的顶点都和图中某条边关联,则为完备匹配[19]。因为最大完全子图中的虚拟机规模不小于数据结点的规模(小于则无解),所以完备匹配是指所有的数据结点都被虚拟机处理。本文采用Hopcroft-Karp算法来解决此问题。该算法是由Hopcroft与Karp一起提出的,是对Hungarian算法(匈牙利算法)的优化,其思想主要是在寻找增广路径的同时寻找多条不相交的增广路径,形成极大增广路径集,然后对极大增广路径集进行增广[18]。NEW-VMA算法在某一阈值下使用回溯法寻找虚拟机的最大完全子图时,一旦完全子图的规模满足数据结点,就及时执行Hopcroft-Karp算法为数据结点匹配虚拟机,若能达到完备匹配,则终止。增加阈值虽然能使团规模增加,降低二分图匹配的阈值,但最大通讯延迟也随之增大。Hungarian算法的时间复杂度是O(n×m)[20],n为二分图中的顶点数,m为二分图中的边数,而Hopcroft-Karp算法的时间复杂度为O(n1/2×m)。 3.4时间复杂度 以下简单陈述通讯延迟的计算复杂度。在含有n1个数据结点,n2个虚拟机与l条边的图中,算法首先确定边的权值种类,最坏情况下时间复杂度为O(l2)。对于l1种边的权值进行排序,最坏情况下的时间复杂度为O(l1lbl1)。在某一阈值下使用回溯法寻找最大完全子图时,最坏情况下时间复杂度为O(n22n2)。因此,算法在最坏情况下的时间复杂度为O(l1n22n2)。通过剪枝函数可以提前判断继续深度优先搜索是否可能得到最优解,抛弃不可能导致合法解的候选解,从而使求解时间大大缩短,提高搜索的效率。 本文评估不同虚拟机分配算法对于通讯延迟的影响。实验在Intel®CoreTMi5-4200M CPU@2.50 GHz 2.49 GHz的处理器上进行,实现了与文献[1]中启发式方法的比较,也实现了与文献[8]中近似算法的比较。实验中使用了与参考文献相同的实验参数。 4.1与启发式算法的比较 在文献[1]的实验中,数据中心内的网络结构上设置有1 024个服务器,将40个数据结点和120个虚拟机随机放置在1 024个服务器的前64、256和1 024个服务器中,即实验中数据结点与虚拟机的分布区间为[1,16]、[1,64]和[1,256]。数据结点和虚拟机的位置一旦确定,则任何一个虚拟机与任一个数据结点或虚拟机之间通讯所经过的交换机数目也就确定。在不同分布区间上,两个服务器之间通讯所经过的最大交换机数如表1所示。 Table 1 Maximum number of switches between two racks表1 两个服务器通讯经过的最大交换机数 两个服务器之间的通讯延迟由这两个服务器通讯所经过的交换机数目支配[8],因此在本文实验中最大通讯延迟用交换机的个数表示。经过更少的交换机意味着通讯延迟更小[7]。数据结点与虚拟机之间或虚拟机与虚拟机之间的通讯延迟为这两个结点所在的服务器进行通讯所经过的交换机数乘以[0.75, 1.25]中的一个随机数。实验将数据结点和虚拟机在每个区间上随机分布20次,并求最大通讯延迟和运行时间。图7、图8分别为在相同实验参数下的最大通讯延迟和运行时间的比较。 Fig.7 Maximum access latencies of two algorithms图7 两种算法的最大通讯延迟 Fig.8 Running time of two algorithms图8 两种算法的运行时间 图7实验结果表明,本文虚拟机分配算法(NEWVMA)与文献[1]中启发式算法(VMA)在3种分布区间上得到的最大通讯延迟相同。但运行时间平均改进了7.49%,如图8所示。本文先根据阈值对最大完全子图的规模进行初步判断,然后再决定是否寻找完全子图。若判断得出虚拟机规模一定不满足数据结点的结论,则不调用回溯法,继续对下一个阈值进行判断,如此可避免阈值过小时对最大完全子图的寻找,从而降低运行时间。 4.2与近似算法的比较 文献[8]中的实验选择的结构为数据中心内常用的4种网络拓扑结构[7],分别是Tree、VL2、Fat-Tree和BCube[21]。在构造Tree结构时,设置接入层交换机的扇出(fan-out)p0为16,汇聚层交换机扇出p1为4。在VL2结构中,设置接入层交换机扇出p0为32。在Fat-Tree结构中,设置交换机的端口数k为16。在BCube中,设置阶数k为1,交换机端口数n为32。根据设置参数可以确定该拓扑结构的大小,即可得知每层交换机数目以及每个接入层的交换机连接的服务器数目。 例如:在Fat-Tree结构中[22],一组接入层和汇聚层的交换机成为一组机架(pod),每个机架中的接入层和汇聚层的交换机构成一个完全二分图。交换机端口数是决定Fat-Tree结构中机架数目、每层交换机数目和连接服务器数目的唯一参数。若有k个端口,则此网络结构中有k个机架,每个机架中有k/2个接入层交换机,k/2个汇聚层交换机,每个机架连接k2/4个核心层交换机和k2/4个服务器。这样共有5×k2/4个交换机和k3/4个服务器。因此,在Fat-Tree结构中,位于第 j个服务器中的虚拟机处理第i个服务器中的数据结点所经过的交换机数Cij为: 在文献[8]的实验中,数据中心内的网络结构上有1 024个服务器。将40个数据结点和120个虚拟机随机放置在1 024个服务器的前16、64、256和1 024个服务器中,即实验中数据结点和虚拟机的分布区间为[1,16]、[1,64]、[1,256]和[1,1 024]。在4种网络结构上的不同分布区间,两个服务器之间通讯经过的最大交换机数如表2所示。 通讯延迟大小由经过的交换机数和[0.9,1.1]之间的随机数而决定。图9的实验结果表明,在VL2上,3-近似算法与2-近似算法所得到的最大通讯延迟相同,当数据结点和虚拟机的分布区间为[1,16]、[1, 256]和[1,1 024]时,NEW-VMA算法与两种近似算法所得到的最大通讯延迟相同,在[1,64]区间上的最大通讯延迟降低了18.18%,在4个分布区间上的平均延迟降低了5.68%。 Table 2 Maximim number of switches between two racks表2 两个服务器通讯经过的最大交换机数 Fig.9 Maximum access latencies of 3 algorithms on VL2图9 在VL2结构上3种算法的最大通讯延迟 在图10中,实验选择的网络结构为Tree结构,当数据结点与虚拟机的分布区间为[1,16]和[1,1 024]时,NEW-VMA算法与两种近似算法所得到的最大通讯延迟相同;在[1,64]和[1,256]区间上,NEWVMA算法所得到最大访问延迟较小。在4个分布区间上的平均通讯延迟降低了10.39%。 Fig.10 Maximum access latencies of 3 algorithms on Tree图10 在Tree结构上3种算法的最大通讯延迟 图11结果表明,在Fat-Tree结构上,当分布区间为[1,64],[1,1 024]时,NEW-VMA算法与两种近似算法所得到的解相同;在[1,16]和[1,256]区间上,NEW-VMA算法所得到最大访问延迟较小。在4个分布区间上的平均通讯延迟降低了9.09%。 Fig.11 Maximum access latencies of 3 algorithms on Fat-Tree图11 在Fat-Tree结构上3种算法的最大通讯延迟 图12表明,在BCube中区间为[1,16]、[1,256]和[1,1 024]时所得到的最大通讯延迟相同,在[1,64]的分布区间上所得到的解较优。在4个分布区间上的平均延迟降低了5.45%。3-近似算法将虚拟机分配问题松弛成3-近似问题,在求解问题时,即使数据结点与虚拟机之间的最大通讯延迟不超过阈值t,但处理数据的虚拟机与虚拟机之间的最大通讯延迟控制在2t内,使得最大通讯延迟在3t范围内,最后得到的可行解的最大通讯延迟可能较大。 Fig.12 Maximum access latencies of 3 algorithms on BCube图12 在BCube结构上3种算法的最大通讯延迟 实验结果表明,在Tree、VL2、Fat-Tree和BCube 这4种网络拓扑结构中3-近似算法与2-近似算法所得到的最大通讯延迟相同,本文算法在这4种网络结构上平均情况下最大通讯延迟分别降低了10.39%、5.68%、9.09%和5.45%。 虚拟机分配是实现云中资源有效调度的首要考虑,有效的分配策略不仅可以减少通讯延迟,减少网络带宽消耗,还可以提高资源的利用率。本文针对虚拟机分配的最大通讯延迟问题,考虑了虚拟机之间互相通讯存在延迟的情况,提出了一种先判断后找团再匹配的算法,较现有的算法,在运行时间和解的性能方面得到改进。在未来的工作中,还将考虑虚拟机之间互相通讯的不同模式。 [1]Alicherry M,Lakshman T V.Optimizing data access latencies in cloud systems by intelligent virtual machine placement[C]//Proceedings of the 32nd IEEE Conference on Computer Communications,Turin,Italy,Apr 14-19,2013. Piscataway,USA:IEEE,2013:647-655. [2]Applying the cloud to big data storage[EB/OL].[2015-04-20].http://www.appistry.com/sites/default/files/downloads/. [3]DeanJ,GhemawatS.MapReduce:simplifieddataprocessing on large clusters[J].Communications of the ACM,2008,51 (1):107-113. [4]Li Xin,Wu Jie,Tang Shaojie,et al.LetƳs stay together:towards traffic aware virtual machine placement in data centers[C]//Proceedings of the 33rd IEEE Conference on Computer Communications,Toronto,Canada,Apr 27-May 2, 2014.Piscataway,USA:IEEE,2014:1842-1850. [5]Li Yunfa,Li Wanqing,Jiang Congfeng.A survey of virtual machine system:current technology and future trends[C]// Proceedings of the 3rd International Symposium on Electronic Commerce and Security,Guangzhou,China,Jul 29-31,2010.Piscataway,USA:IEEE,2010:332-336. [6]Hyser C.McKee B,Gardner R,et al.Autonomic virtual machine placement in the data center[R].HPLaboratories,2008. [7]Meng Xiaoqiao,Pappas V,Li Zhang.Improving the scalability of data center networks with traffic-aware virtual machine placement[C]//Proceedings of the 2010 IEEE Conference on Computer Communications,San Diego,USA, Mar 14-19,2010.Piscataway,USA:IEEE,2010:1-9. [8]Kuo J J,Yang H H,Tsai M J.Optimal approximation algo-rithm of virtual machine placement for data latency minimization in cloud systems[C]//Proceedings of the 33rd IEEE ConferenceonComputerCommunications,Toronto,Canada, Apr 27-May 2,2014.Piscataway,USA:IEEE,2014:1303-1311. [9]ZhengYang,CaiLizhi,HuangShidong,etal.VMscheduling strategies based on artificial intelligence in cloud testing [C]//Proceedings of the 15th IEEE/ACIS International Conference on Software Engineering,Artificial Intelligence,Networking and Parallel/Distributed Computing,Las Vegas, USA,Jun30-Jul2,2014.Piscataway,USA:IEEE,2014:1-7. [10]Gibbons A.Algorithmic graph theory[M].Cambridge,UK: Cambridge University Press,1985. [11]Miller G A.WordNet[EB/OL].Princeton University(2009) [2015-04-20].http://wordnet.princeton.edu. [12]Bron C,Kerbosch J.Finding all cliquese on an undirected graph[J].Communications of theACM,1973,16(9):575-577. [13]Kurose J F,Ross.K W,Computer networking:a top-down approach[M].5th ed.Boston,USA:Addison-Wesley Publishing Company,2009. [14]Understanding switch latency[EB/OL].[2015-04-20].http:// www.cisco.com/en/US/prod/collateral/switches/ps9441/ps11541/ white paper c11-661939.html. [15]Speed reduction by distance[EB/OL].[2015-04-20].http:// www.numion.com/calculators/Distance.html. [16]Alicherry M,Lakshman T.Network aware resource allocation in distributed clouds[C]//Proceedings of the 2012 IEEE Conference on Computer Communications,Orlando,USA, Mar 25-30,2012.Piscataway,USA:IEEE,2012:963-971. [17]van Lint J H,Wilson R M.A course in combinatorics[M]. Cambridge,UK:Cambridge University Press,2001. [18]Hopcroft J E,Karp R M.An5/2algorithm for maximum matchings in bipartite graphs[C]//Proceedings of the 12th Annual Symposium on Switching and Automata Theory, East Lansing,USA,Oct 13-15,1971.Piscataway,USA:IEEE, 1971:122-125. [19]Kim W Y,Kak A C.3-D object recognition using bipartite matching embedded in discrete relaxation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991, 13(3):224-251. [20]Burkard R E,Cela E.Linear assignment problems and extensions[M]//Handbook of Combinatorial Optimization:Supplement VolumeA.Springer US,1999:75-149. [21]Guo Chuanxiong,Lu Guohan,Li Dan,et al.BCube:a high performance,server-centric network architecture for modular data centers[C]//Proceedings of the 2009 ACM SIGCOMM Conference on Data Communications,Barcelona,Spain,Aug 17-21,2009.NewYork,USA:ACM,2009:63-74. [22]Leiserson C E,Fat-trees:universal networks for hardwareefficient supercomputing[J].IEEE Transactions on Computers, 1985,100(10):892-901. GAO Renfei was born in 1990.She is an M.S.candidate at Tianjin Polytechnic University.Her research interests include data center and high performance architecture. 高任飞(1990—),女,河南商丘人,天津工业大学硕士研究生,主要研究领域为数据中心,高性能体系结构。 WU Jigang was born in 1963.He received the Ph.D.degree from University of Science and Technology of China in 2000.Now he is a chair professor at Guangdong University of Technology.His research interests include theoretical computer science and high performance architecture. 武继刚(1963—),男,江苏沛县人,2000年于中国科学技术大学获得博士学位,现为广东工业大学计算机科学与技术学院特聘教授,主要研究领域为理论计算机科学,高性能体系结构。在国际重要学术期刊与会议上发表200余篇学术论文,主持国家自然科学基金课题、教育部博士点科研基金课题。 ZHOU Ying was born in 1979.She is a Ph.D.candidate at Tianjin Polytechnic University.Her research interests include high performance architecture and faults tolerance. 周莹(1979—),女,天津人,天津工业大学博士研究生,主要研究领域为高性能体系结构,容错设计。 ZHANG Yaoguo was born in 1990.He is an M.S.candidate at Tianjin Polytechnic University.His research interests include data center and faults tolerance. 张耀国(1990—),男,江苏连云港人,天津工业大学硕士研究生,主要研究领域为数据中心,容错设计。 Virtual MachineAssignment for Minimizing Data Latencyƽ GAO Renfei1,WU Jigang2+,ZHOU Ying1,ZHANG Yaoguo1 In the modern data centers based on virtualization,virtual machine(VM)assignment is the primary research topic to efficiently schedule the cloud resources.In cloud systems,the big data are partitioned and then stored over several data nodes(DNs)for being processed by VMs.Thus,there is access latency among DNs and their assigned VMs.Meanwhile,the access latency among the pairs of assigned VMs also exists for the computing result collection.Different assignment strategies of VMs for DNs result in different maximum access latency.It has been proved that the assignment problem of VMs(VMA)to minimize the maximum access latency is of NP-hard.This paper proposes a new algorithm for VMA.The proposed algorithm initially determines if there exists enough number of VMs which can communicate with each other under a certain threshold limit in access latency.If yes,an efficient backtrack algorithm is then employed to find cliques consisted of VMs under this threshold.After that,the Hopcroft-Karp algorithm is used to assign the VMs in the clique for DNs,in order to save the computing time by significantly reducing the solution space.Extensive experimental results show that the maximum access latency is reduced 10.39%,5.68%,9.09%,5.45%on average,respectively,on the popular four network architectures,Tree,VL2,Fat-Tree and BCube,in comparison to the state-of-the-art approximation algorithms. data center;virtual machine assignment;access latency;complete subgraph 2015-06,Accepted 2015-08. 10.3778/j.issn.1673-9418.1507043 A TP302 *The Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No.20131201110002(高等学校博士学科点专项科研基金). CNKI网络优先出版:2015-08-28,http://www.cnki.net/kcms/detail/11.5602.TP.20150828.1505.004.html
4 实验结果及分析








5 结束语




1.School of Computer Science and Software Engineering,Tianjin Polytechnic University,Tianjin 300387,China 2.School of Computer Science and Technology,Guangdong University of Technology,Guangzhou 510006,China +Corresponding author:E-mail:asjgwucn@outlook.com
