协变量缺失下基于结构EM算法因果网模型选择

马　蔷，尚来旭，张冬阳，单　娜

(长春工业大学 基础科学学院， 吉林 长春　130012)



协变量缺失下基于结构EM算法因果网模型选择

马蔷，尚来旭，张冬阳，单娜*

(长春工业大学 基础科学学院， 吉林 长春130012)

针对NSCOT数据,选用了结构EM算法对模型进行选择。经过具体的计算和分析得到结论，一个人的身体素质和运送到医院的时间都会对患者的生存产生直接的影响，而受伤的严重程度只对患者的生存产生间接的影响。

协变量缺失； 结构EM算法； 模型选择

0　引　言

运用NSCOT(TheNationalStudyonCostsandOutcomesofTrauma,NSCOT)数据[1]进行协变量缺失下因果网模型选择的研究，NSCOT是美国国内医疗花费和创伤治疗结果研究的相应的数据。这个研究主要是为了得到关于创伤中心更好的信息,其针对5 000名18～84岁，来自12个州69家医院的创伤病人，通过对其医疗花费和治疗结果的研究达到相应目的。近年来，很多国内外的学者都对这个数据进行了不同方面的研究。Frangakis[2]等利用主分层设计对NSCOT的数据进行了研究，其得出结论：对于身体状况不好的人来说，一个有效的治疗是非常重要的。Egleston[3]等对由于死亡使重要混杂缺失情况下的生存者平均因果效应进行了研究。通过对NSCOT进行分析，证明了生存者平均因果效应的估计都要比通常的回归好，同时无论是否被分配治疗，有创伤中心的医疗机构的生存率都要高于无创伤中心的医疗机构的生存率。Wang[4]等利用NSCOT数据对5个不同的估计量进行了比较，其认为在没有创伤中心的医疗机构的死亡率近似为有创伤中心的医疗机构的死亡率的两倍。Yan[5]等在文献[2]研究的基础上进行了改进，放宽了原有的假设，对NSCOT数据进行了研究，得到了因果效应的边界，对于身体状况差的人来说，一个有效的处理是更好的。虽然有很多人针对这个数据进行了分析，并且或多或少地解释了其中所暗含的一些因果关系，但是并没有阐明各个变量间的因果结构关系，而文中将主要研究NSCOT数据的因果网模型选择问题。由于所给出的数据是带有缺失的，所以，我们不能用一般的方法进行模型选择。通常来说处理缺失数据的方法有均值插补、多重插补等，但是补值的方法会影响变量间的相互关系，对不完全的信息进行插补的时候，或许会改变其原始数据的信息系统，从而对以后的分析存在潜在的影响，所以，文中利用结构EM(structuralEM)算法[6]对模型进行选择。结构EM算法选择模型结构依赖于惩罚似然评分，文中提到的评分函数是BIC评分。

1　符号和定义

文中所用数据如下：

A代表身体素质，A=1代表身体素质不好，A=0代表身体素质良好；

Z代表处理，即从案发地送到医院的时间，Z=1代表运送时间<10min，Z=0代表运送时间≥10min；

X代表受伤的严重程度，X=1代表伤势轻微，X=0代表伤势严重；

S代表生存状态，S=1代表生存，S=0代表死亡。

由数据的产生背景可以认为变量的顺序为A,X,Z,S。对变量进行因果关系建模时，其基本模型如图1所示。

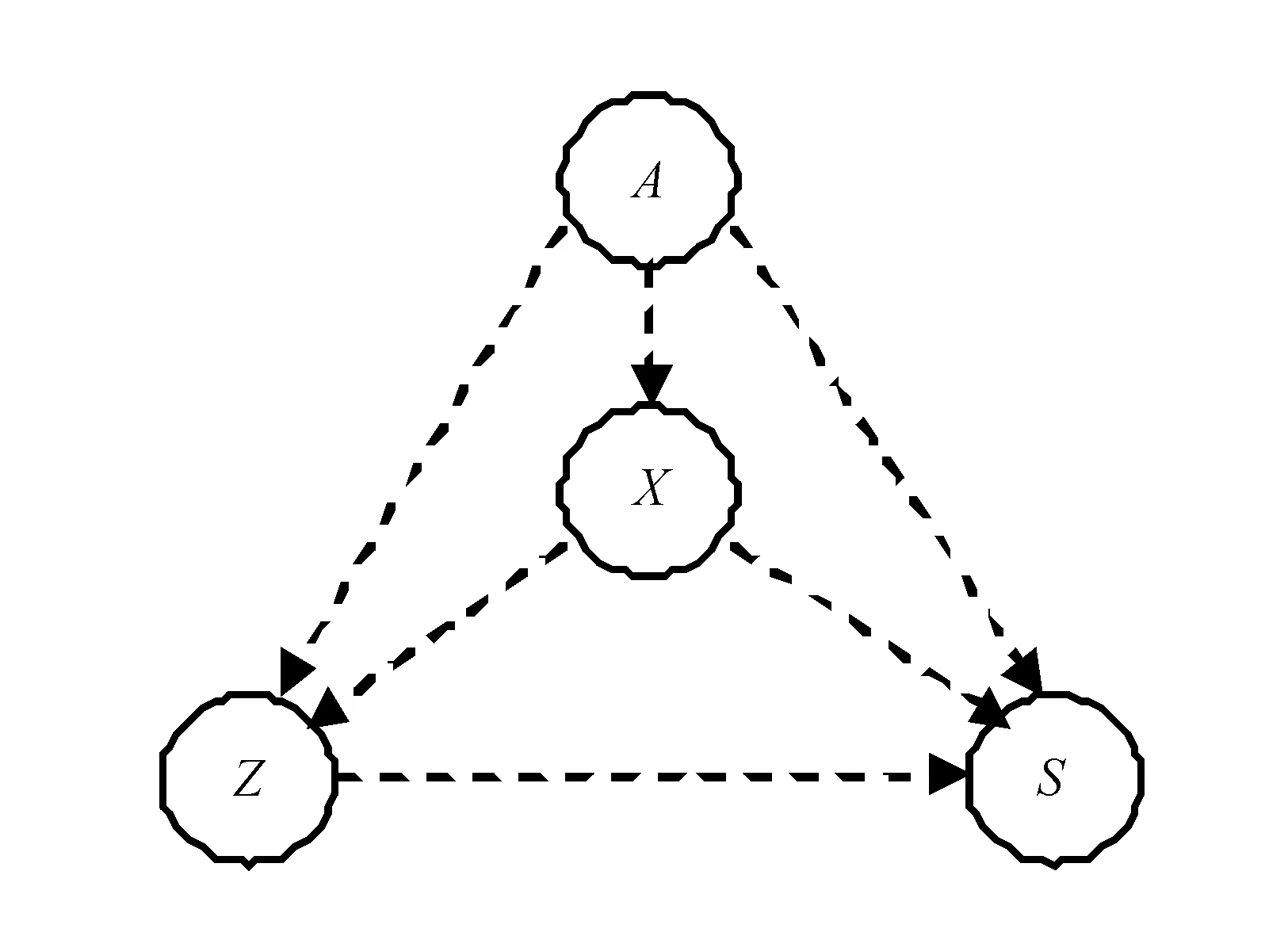
图1　基本模型

图中，虚线表示该边可能存在，也可能不存在。

最简单的模型如图2所示。

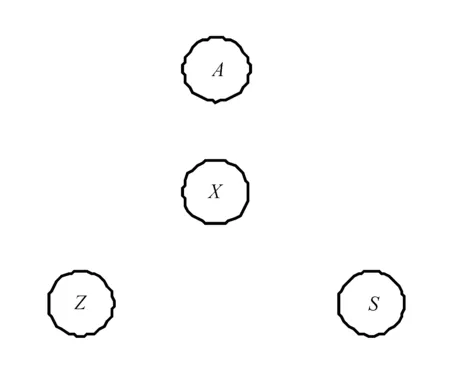
图2　零模型

此时各变量之间都无因果关系。

而最复杂的模型如图3所示。

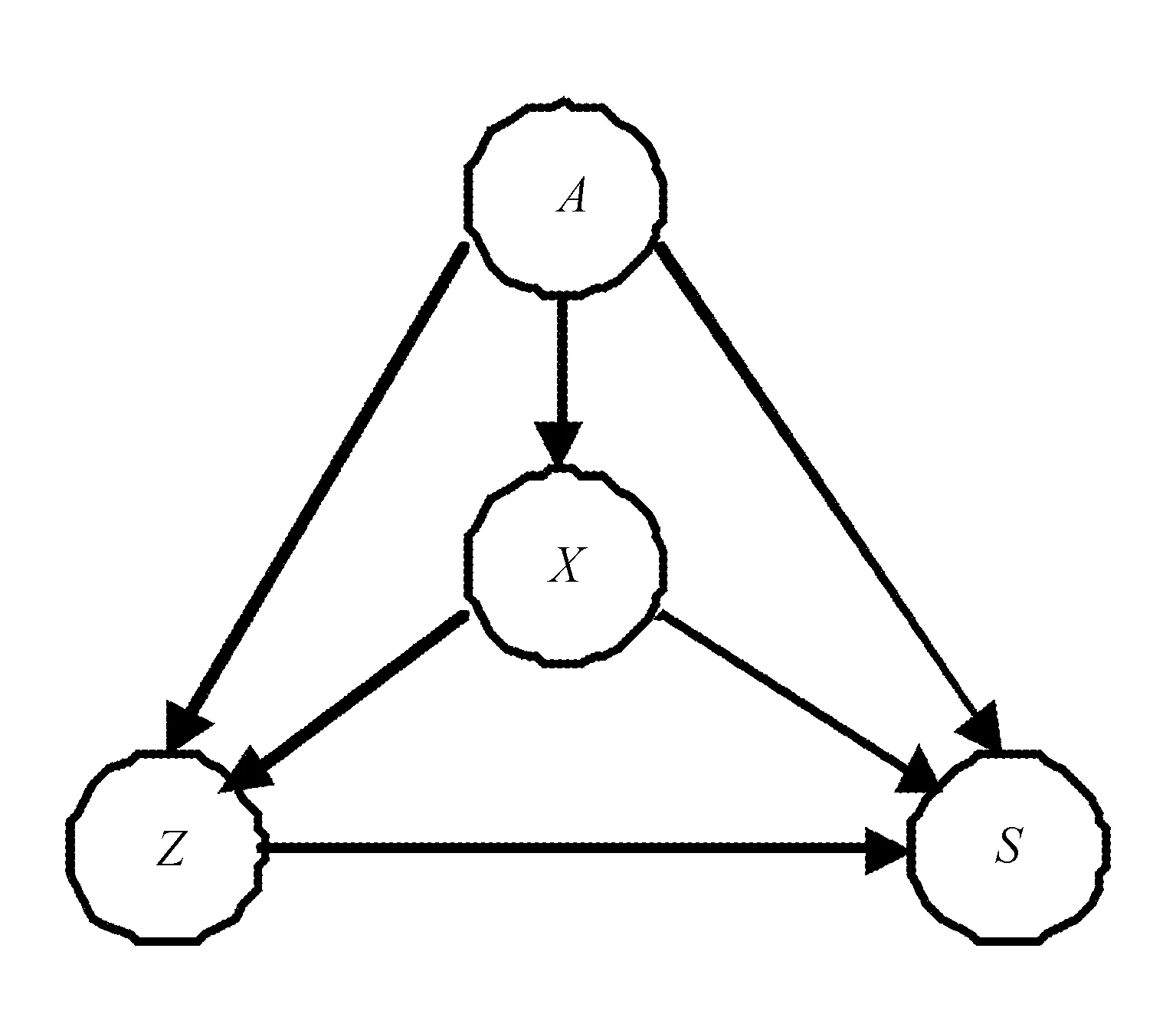
图3　全模型

此时各个可能的因果关系都存在。

所有的可能模型共有26=64种。对于图3中的全模型，(A,X,Z,S)的联合概率分布函数表示如下：

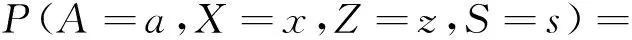
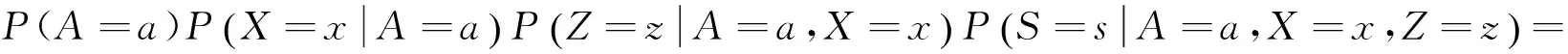
其中

对于其他模型下，(A,X,Z,S)的联合概率分布函数基于模型结构有类似的分解。

2　结构EM算法的基本思想

结构EM算法是由EM算法演化而来的，在其步骤的实现过程中与EM算法有很大的相似性。基本步骤如下：

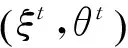
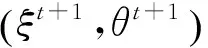
在这个过程中，有两点需要注意。首先，在EM算法中，根据填补后的完整数据Dt对参数进行一步优化就可以得到此时的最优的参数。但是在结构EM算法中，根据Dt进行一步优化不一定得到此时的最优模型。其次，由于固定模型结构进行一步参数优化比进行一步结构优化要简单，所以，结构EM算法并不是每次迭代都同时进行结构和参数的优化，而是在使模型结构不变的情况下，经过参数优化后再对结构和参数同时优化。

3　实证分析

NSCOT主要是关于5 000名18～84岁，来自12个州69家医院的创伤病人的数据。我们将采用文献[5]所使用的部分数据，见表1。

在得到似然函数期望的条件下，利用R软件[7]对其参数进行估计，并计算其BIC的值。经过多次估计和比较，再选取BIC值最小的模型作为该问题的最优模型，此时各参数的估计值和模型见表2和图4所示。

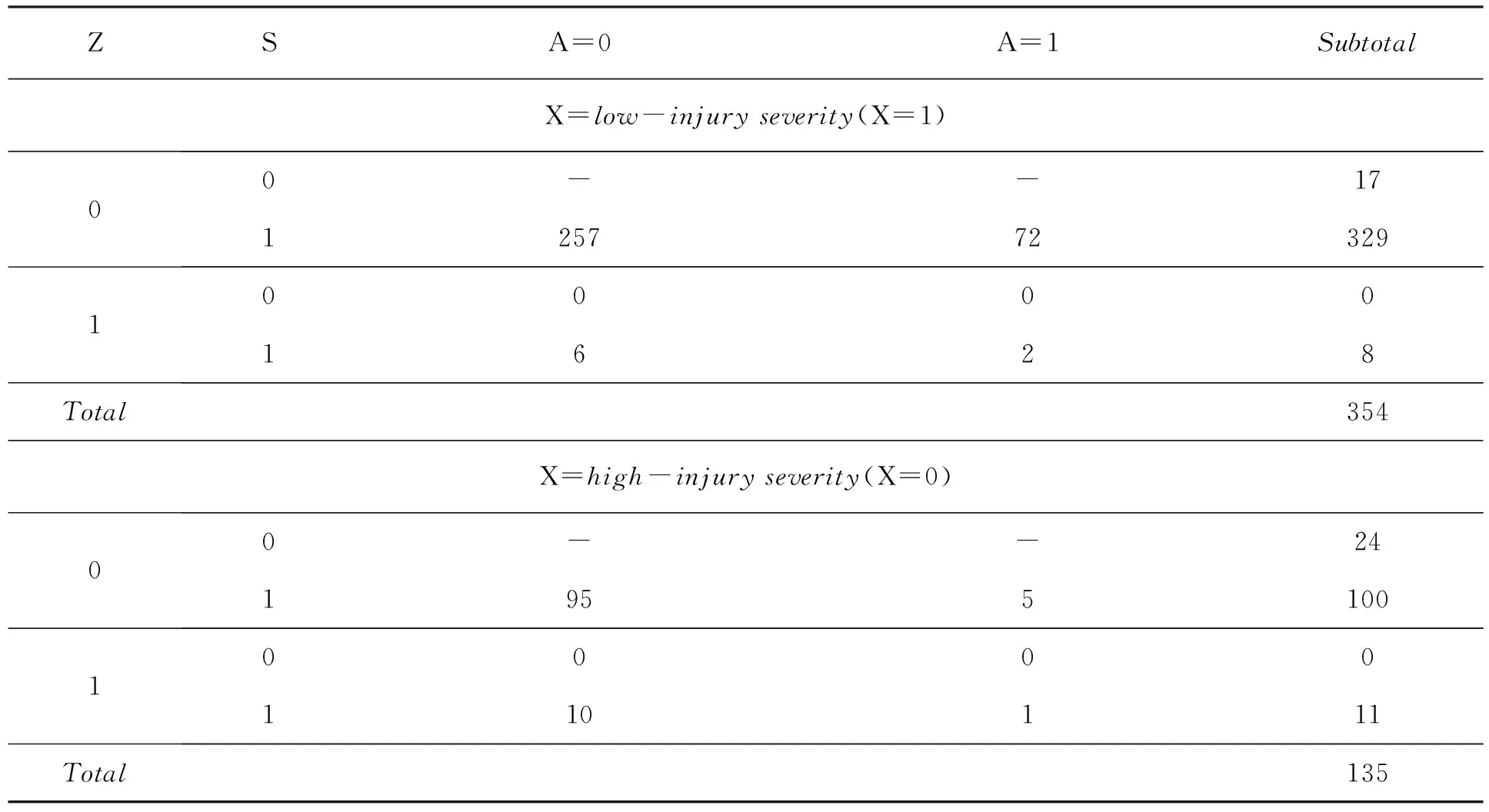
表1　NSCOT数据整理结果

注：“-”代表缺失的协变量观测值。

表2　最优模型下的参数估计值

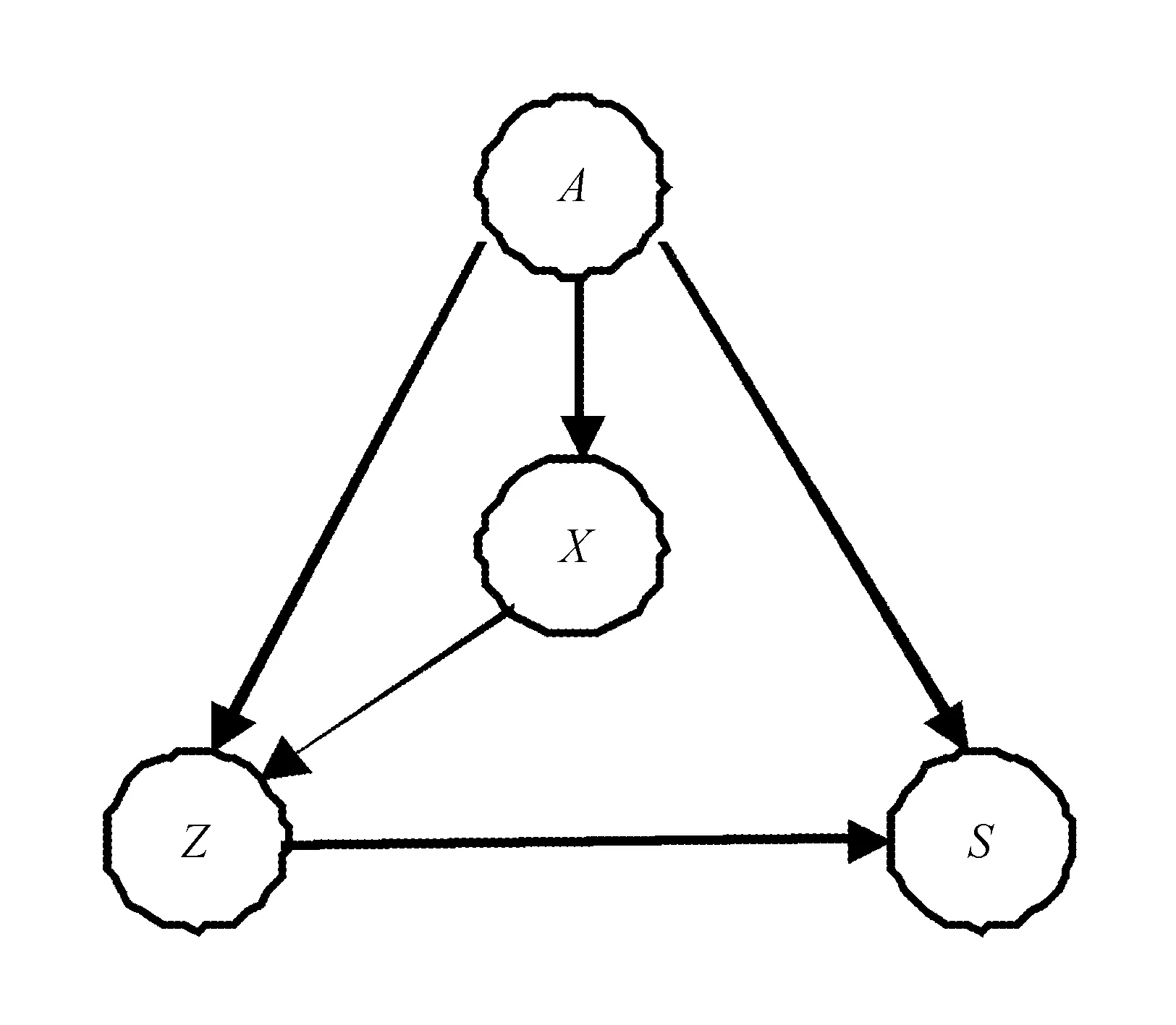
图4　最优模型

4　结　语

从数据中可以发现，送往医院的时间Z与生存状况S是有直接关系的。当及时送达医院时,患者是不会死亡的，而送达医院的时间>10 min时，病人一定会死亡。这在最优的因果网模型中体现为Z对S有直接的影响。同时，在最优的因果图中可以看出，一个人的身体素质A是非常重要的。当一个人的身体素质不好时，即使不是非常严重的伤势也会使其死亡；相反，当一个人拥有好的身体素质，即使伤势严重也可能存活。在现实生活中，一个人的身体素质可以表现性别、工作和身体外部状态等多个方面，一般情况下，年轻且身体强壮的男性在受伤的情况下存活的概率自然会大一些，这个常识与我们所得到的因果图也是吻合的。同时，在因果图中可以看出，一个人的身体素质和受伤的严重情况也会在一定程度上影响病人的运送时间。这可能体现了地域特征对病人运送时间的影响。最后，图中显示，身体素质对受伤的严重程度有直接的影响，这也是符合正常的生活常识的。

综上所述，通过结构EM算法选择使BIC值达到最小时的模型是合理的，与实际情况相符。

[1]Ellen J MacKenzie, Frederick P Rivara. The national study on costs and outcomes of trauma[J].The Journal of Trauma-Injury, Infection, and Critical Care,2007,63:54-67.

[2]Constantine E, Frangakis, Donald B Rubin. Principal stratification designs to estimate input data missing due to death[J]. Biometrics,2007,63:641-662.

[3]Brian L Egleston, Daniel O Scharfstein, Ellen Mac Kenzie. On estimation of the survivor average causal effect in observational studies when important confounders are missing due to death[J]. Biometrics,2009,65:497-504.

[4]Weiwei Wang. Causal inference in outcome-dependent two-phase sampling designs[J]. Journal of the Royal Statistical Society,Series B,2009,71:947-969.

[5]Wei Yan, Yaqin Hu, Zhi Geng. Identifiability of causal effects for binary variables with baseline data missing due to death[J]. Biometrics,2012,68:121-128.

[6]和超.基于结构EM的隐变量模型学习方法[D].昆明:云南大学,2015.

[7]薛毅,陈丽萍.统计建模与R软件[M].北京:清华大学出版社,2007:58-60.

Structural EM based causal network model selection withdefaultcovariate

MA Qiang，SHANG Laixu，ZHANG Dongyang，SHAN Na*

(School of Basic Sciences, Changchun University of Technology, Changchun 130012， China)

WithNSCOTdata,structuralEMalgorithmisusedformodelselection.Calculationsandanalysiscomestoaconclusionthandirectinfluenceisfromboththephysicalqualityofapatientandthetransfertimetohospitalwhileindirectinfluenceonlyfromtheinjurydegreeofthepatient.

defaultcovariate;structuralEMalgorithm;modelselection.

2016-01-10

国家自然科学基金资助项目(11571050，11401047)

马蔷(1992-)，女，汉族，内蒙古赤峰人，长春工业大学硕士研究生，主要从事因果推断方向研究,E-mail:292094969@qq.com. *通讯作者：单娜(1981-)，女，汉族，吉林长春人，长春工业大学副教授，博士，主要从事因果推断图模型技术方向研究,E-mail:48978645@qq.com.

10.15923/j.cnki.cn22-1382/t.2016.4.16

O212

A

1674-1374(2016)04-0396-05