基于认知过程分析的数学选择题编制探究

张磊

（韩山师范学院数学与统计学院，广东潮州　521041）

基于认知过程分析的数学选择题编制探究

张磊

（韩山师范学院数学与统计学院，广东潮州521041）

通过案例研究提出了一个侧重于描述学生在问题解决过程中认知经历的思维模式：解读→表征→构建→实施.为提升数学教师的测试题编制能力，将该思维模式应用于数学选择题中干扰项的编制上，借此数学教师可揭示出学生在问题解决过程中每个认知阶段的根本性错误.另外，该思维模式可为数学选择题这个范畴的测试题编制提供统一标准，以此保证数学教师编制的数学选择题在测试时能得到一致的反馈结果.

问题解决；认知；思维模式；数学选择题；干扰项

1　问题的提出

编制数学测试题是数学教师钻研教材、熟悉学生的途径之一，是数学教学工作重要的组成部分.学生解答一道高质量数学测试题，能了解自己的学习效果，数学教师通过过程性诊断可以更好地把握学生在运用数学知识的过程中所展现出来的潜质或缺陷，为数学教师提供反思教学的依据.然而，目前中小学数学测试题的编制存在着一些不容忽视的问题，如有些数学教师图省力，对现成试卷“既不研究，又未修改”拿来就用；有些数学教师所编制的测试题“背景”不切实际，忽视思想性；有些数学教师所编制的测试题超标挫伤学生积极性等等.上述种种现象致使测试的负面效应加大，加重了学生的学习负担，影响了教学质量的提高.基于上述背景，本文试图就数学测试题中选择题的编制作一粗浅探讨，希望借此能帮助数学教师提升自身的数学测试题编制能力，进而使得所编制的试题更准确、更科学，对数学教学真正起到正确评估和导向作用.

张奠宙教授在《数学教育概论》中谈及数学选择题编制时表示，数学选择题的编制应重点关注干扰项的高效设计，其设计效率关乎着数学选择题的编制质量.［1］那么，如何能保证自己编制的干扰项的高效性呢？很显然，学生在数学问题解决中都会经历一个连续的认知过程，如果数学教师能够把握住学生在数学问题解决过程中认知经历的思维模式，进而把干扰项连续地设置在学生所经历的认知阶段上，通过缜密的分析，数学教师就能够精确地根据学生的错误类型推断出学生在数学问题解决过程中的阶段性认知障碍，提出学习和教学的改进建议.为此必须先理清学生在数学问题解决过程中认知经历的思维模式.

2　一个侧重于描述学生在问题解决过程中认知经历的思维模式

长期以来，许多数学教育家、心理学家以及哲学家，通过剖析问题解决这一复杂的思维过程，提出了若干模式.例如，在国外，杜威（Dewey）在《我们怎样思维》一书中将问题解决的思维过程分成5个阶段：问题的感觉→问题的界定→问题解决的假设→对问题及其解决方法的逻辑推理→用行动检验这些假设；［2］英国心理学家华莱士（Wallace）在《思想的艺术》一书中提出问题解决4阶段模式：准备阶段→酝酿阶段→明朗阶段→验证阶段；［3］美籍匈牙利数学家、教育家波利亚（Polya）在《怎样解题》一书中将解题的思维过程分为如下4个步骤：理解问题→拟订方案→执行方案→回顾；［4］美国心理学家纽威尔和西蒙（Newell&Simon）提出通用问题解决模型：问题解决经历发现问题→分析问题→提出假设→验证假设；［5］等等.在国内，当代学者蔡燊安和李祝华提出问题解决四阶段模式：定向→逼近→成型→引深；［6］吴鸿业等提出问题解决思维模式假设流程图；［7］等等.这些思维模式主要注重应用的“一般性”，很少具体化到数学问题解决的认知过程中，而且侧重点在科学理论研究，而不是直接具体落实到学生的实际解题中，或者说它们各个阶段的重点是描述教师如何引导学生去解决问题，主要侧重于为教师教学服务，而不是重在为学生的解题服务.显然，这与笔者所要寻找的侧重于描述学生在问题解决过程中认知经历的思维模式不同.为此，笔者参考美国学者Silver等人的研究报告开展如下的案例研究：［8］

案例收集：首先，在本市城南小学等学校选取120名3年级到6年级学习态度积极且学习成绩优秀的学生，给予充足的时间，让他们基于自身的思考设计出一道数学问题，同时注明问题的解决方案.然后，收集学生资料并进行类型梳理，其中重点梳理出具有如下特征的4类案例：①数学问题设计不完整，同时，给出的解题方案不正确；②数学问题设计完整，同时，给出的解题方案正确；③数学问题设计完整，但是，给出的解题方案低于或超过自己的年纪水平；④数学问题设计完整，但是，在解题方案中使用了不恰当的解题方法.

案例分析：针对梳理出的四类案例，笔者借助反思、访谈等形式重点探究学生的设计和解题思路，尽量总结他们解题背后所蕴含的一般规则.在整个案例分析过程中，最重要的方法是反思，通过反思，可以突显学生解题中的一些认知过程，帮助笔者更好地解释学生的认知经验.下面，笔者从四类案例中列举出四个典型案例，通过它们揭示解题过程中某一认知阶段的重要性.

典型案例1：刘敏（5年级）

案例分析：显然，刘敏设计的问题题意不完整，主要表现在问题中已知量和未知量的关系不能明确表示.于是，在解题过程中，她用自己的方式来解读这道题，添加了一些问题中并没有给出的条件，如“7队与8队参加第一轮的对决比赛，获胜的球队取得进入决赛的资格”等等.因此，虽然刘敏给出的解题过程是正确的，但它只是完整解决方案的一部分，也即是只分析了一种可能发生的情况.从另一角度来分析，说明刘敏对该问题的题意解读失败.

典型案例2：陈洁（6年级）

案例分析：很显然，陈洁给出的问题设计和问题解决都是正确的.在随后的访谈中，笔者提出两个问题.问题一：“两个水池真的会在某一时刻保持相同水量吗？”陈洁通过手势来描述，从而形象地表明了水位在A水池（下降）和B水池（上升）的变化，因此，她认为所设计的问题是有解决方案的；问题二：“该问题设计为什么花费那么长时间？”陈洁解释说她得慎重选择数字（如问题中的10 L/min、15 L/min），以确保这两个水池的水位变化是有增有减.通过陈洁对问题的回答说明她构思和解读问题时，会把相关数据与问题所描述的现象联系在一起，从心理学角度说明她已建立了与问题相关的心智模式.

典型案例3：周伟（3年级）

案例分析：显然，周伟知道所设计问题中的年龄是逐年变化的，也即成功建立了与问题相关的心智模式，但他不能构思出一个方程（数学模型）来解决该问题，也即没有构建起和心智模式对应的数学模型，这也是为什么他只能通过一步步试验来解决这道题.

典型案例4：黄悦（6年级）

案例分析：显然，年龄之间的差距是保持不变的！然而，从解题过程可以看出，黄悦并没有意识到这个事实.通过访谈笔者获知，他在设计这个问题时，已经预想好了用“问题解决”中的方程式来解题，换句话说，他是想用“问题解决”中的方程式来设计一道题.所以这妨碍了他对所设计问题的再认识，使他无法获得最优（最直接）的解决方案.

基于上述案例分析，笔者归纳出学生在数学问题解决过程中经历的四个认知阶段：

解读：找出问题（文字表述）所告知的信息并理解.一般情况下，一个数学问题中包含的信息有：背景（问题的发生或问题情景的描述）、数据（已知量和未知量）、运算形式（题意中蕴含的隐形数学操作，如尺规作图，切割变形等）和约束条件（陈述背景、数据以及运算形式之间的关系）.

在典型案例1中，刘敏并不重视问题中数据和约束条件的设计与解读.例如，用参赛球队的编号来设置一些回合比赛是不完整的，这可能会意味着一些球队没有比赛对象，所以他们没办法参与到比赛中去.又如，她假设“7队与8队对决中赢得的球队取得进入决赛的资格”，问题中并没有提及这样的约束条件.然而，典型案例1的设计与解决给我们传递了一个非常重要的信息：问题解决过程中“解读”阶段的重要性.

表征：把问题中的数据（已知量和未知量）、运算形式等信息转化为自己熟悉的方式呈现.用理解的方式来审题会形成一种心智模式，这种心智模式是引导学生如何解决问题的思维方式，它是一种系统性的归纳展示，一般由形象思维能力、空间想象能力、分析能力、归纳能力、实践能力等组成.这种思维模式还可以继续转换成学生更容易理解的形式，如图形表示、设置活动等.

在典型案例2中，首先，陈洁通过手势活动（一种更容易理解的形式）表达她对问题中水位变化的理解，这说明她自己有一种对两个水池中水位变化的表征方法.接着，陈洁描述在设计问题时得慎重选择数字，以确保这两个水池的水位变化有增有减，这说明她能够把相关数据与问题所描述的现象联系在一起.这些都意味着陈洁成功地为她设计的问题建立起了一个心智模式.

构建：基于问题的解读和表征，学生需要构建起对应的数学模型.所指的数学模型可以是：等式；方程组；用图形表示的一些步骤；各种计算算法等.

在典型案例3中，虽然周伟成功经历了所设计问题的解读阶段和表征阶段，但他没有构建出与心智模式对应的数学模型，因此，他只能通过一步步试验来解决这道题.

实施：在成功构建起数学模型的基础上，应用特定方法（例如：计算、证明、构造、猜想等）得出实际问题解决方案的阶段.由于该阶段是依据自己已经掌握的方法，在确定的情况下对某些已知条件的应用，笔者把它叫做实施.

在典型案例4中，通过与黄悦访谈获知，他是用一个特定方程式（预想好的）来设计问题的，导致他在实施阶段没意识到问题本身的最优解.

综上，本文提出一个侧重于描述学生在问题解决过程中经历认知阶段的思维模式（见图1）：学生在解题时，首先会解读问题（文字表述）；然后搜索数据（已知量和未知量）与运算形式之间的关系，并转化为自己熟悉的表征方式（心智模式）；接着构建出一个适合该问题的数学模型；最后使用特定的方法求出问题的解决方案.

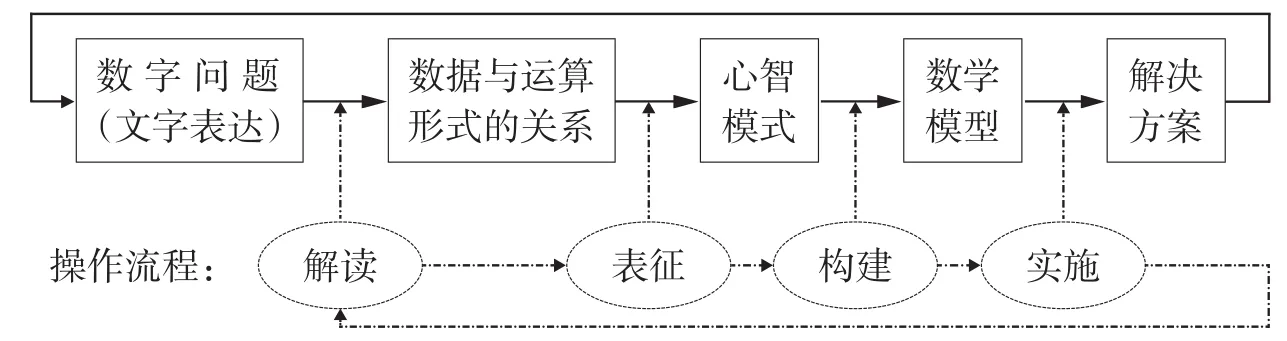
图1　描述学生在问题解决过程中认知经历的思维模式

思维模式中的四个阶段呈递归性原则，也就是说，学生在解决一个问题时，需要按线性顺序通过它们.显然，数学教师可借助该思维模式获得学生的问题解决能力模式，尤其是可以由学生在某一阶段的错误行为挖掘出学生在该阶段的认知故障.同时，考虑到学生阶段性认知能力的培养，依据该思维模式，数学教师可以通过提出具体问题来特别关注学生的某一认知阶段，以满足针对性教学目标的需要.

3　依据上述思维模式，编制高质量数学选择题

由上述讨论可知，侧重于描述学生在问题解决过程中认知经历的思维模式可用于编制数学选择题中的干扰项，下面笔者具体通过两个案例进行应用讨论.

应用案例1：根据数学选择题题干信息有效编制其干扰项

注：事实上，学生在问题解决过程中的每个认知阶段的错误行为各有不同，难以详述.因此，笔者在分析学生在各个认知阶段出现的错误情形时，只描述一种在揭示学生阶段认知故障上具有一定代表性的错误行为.

阶段（一）：解读

要想了解学生在解读阶段出现的问题，重点在于阐述题干文字信息中数据与运算形式之间的基本关系.在该问题的解读中，笔者认为学生必须经历这样一个认知过程：三角形的形成过程是从一个大的三角形连续过渡到一个小的三角形，而三角形面积的求解过程则是由小三角形的面积到大三角形的面积的一个转换.如果缺失这样的解读，学生可能只是对文字表述有一个粗略的感知过程：已知△ABC，找出各边中点，连接成新的三角形，操作三次.进而有意识地将题干中唯一的数字（32）二等分了三次，得出第一个干扰项4.相应的，选择了干扰项4的学生可以清楚地表明自己对这道题的题意解读失败.否则，这个干扰项是可以立即排除的，因为△ABC的面积（整体）不可能小于△A3B3C3面积（一部分）.

阶段（二）：表征

当顺利通过问题解读阶段后，学生会进入问题表征阶段.在该阶段，学生会把解读信息转化为自己熟悉的认知方式来呈现，即把题干中的文字信息转化为自己绘制的对应图形，其中绘制图形的过程涉及重复（三次）相同规则的分割（绘出三角形各边的中点，再由三个中点连接成新的三角形）.什么情况会表明学生对该试题出现思维表征功能障碍呢？也即是对该图形的理解产生“扭曲”呢？例如，学生没考虑到三角形的区域变得越来越小，而是有意识地认为图形中各个部分的面积相等（△ABC被分成十个不相交的且面积相等的三角形），进而计算得出第二个干扰项320.

阶段（三）：构建

笔者认为，在学生成功经历上述两个认知阶段后，他们能够意识到本题所涉及数学模型的重点不是中位线和全等三角形，而是相似三角形.什么情况会表明在学生的头脑中没有构建好相应的数学模型呢？例如，学生误认为相似三角形的边长比等于它们的面积比，也即学生由，计算得出第三个干扰项256.

阶段（四）：实施

当数学模型构建成功后，还需根据实际试题的具体语境，应用特定方法得出试题的解决方案.本实施阶段主要包括三个解题步骤，即把△A3B3C3的面积连续三次乘以4.那么，在本阶段哪里会发生错误呢？例如，学生在压缩上述三次连续计算步骤时，可能会导致计算式32×43被32×4×3取代，这样就会有第四个干扰项384.

综上所述，笔者编制出如下问题选项：

应用案例2：优化编制某数学测试卷中一道选择题中的干扰项

很显然，对于一道数学选择题中干扰项的编制结果并不是唯一的，通常，都是基于预先试验（或推测）来确定的与此有关的错误选项.在没有与该试题编制者直接面谈的前提下，笔者尝试分析试题中干扰项（表1）设置的意义：

表1　

总体上，笔者认为上述干扰项中内含的错误源呈现出重复性、片面性等特点，价值不大.当然，对一个学生来说，在解这道题时，选取试题编制者所预期的任一干扰项都是有可能的.但用一个更有效的策略来编制试题中的干扰项，往往可以更加系统地反映学生的错误源，进而帮助数学教师更加高效地捕捉学生在问题解决过程中的阶段性认知障碍.特别是，在缺乏与学生直接互动的前提下，高效的试题编制能够使得数学教师得到更有效的问题反馈，利于开展接下来的针对性训练.下面笔者基于“描述学生在问题解决过程中认知经历的思维模式”对上述数学选择题中的干扰项进行优化编制.

阶段（一）：解读

同理，要想了解学生在解读阶段出现的问题，重点在于阐述题干文字信息中数据与运算形式之间的基本关系.在该问题的解读中，笔者认为学生必须经历这样一个认知过程：理解题干中数据4与 1003之间的运算关系，即明确41003是由数学运算简化而来的.如果缺失这样的解读，学生可能只是对题干中的文字表述有一个粗略的感知过程，仅仅着眼于“数”的字面，进而有意识地用“41003”取代了“41003”，这种失败的解读会导致出现第一个干扰项03.

阶段（二）：表征

当顺利通过问题解读阶段后，学生会进入问题表征阶段.在该阶段，学生会把解读信息转化为自己熟悉的认知方式来呈现，即把题干中的41003转化为自己更容易理解的认知方式4→×416→×464→×4256….什么情况会表明学生对该试题出现思维表征功能障碍呢？也即是把题干中的41003转化为一种“扭曲”的认知方式呢？例如，学生有意识地把41003转化为4×1003（“扭曲”的认知方式）来呈现，进而计算得出第二个干扰项12.

阶段（三）：构建

笔者认为，在学生成功经历上述两个认知阶段后，他们能够意识到本题所涉及数学模型的重点是周期性计算.什么情况会表明在学生的头脑中没有构建好相应的数学模型呢？例如，在本题所有的周期性计算中，学生本应只关注每一步每一个结果的最后两位数，如果这种心理构建缺失，由于题中涉及的计算序列越来越大，导致计算的过程变得越来越难，这种计算困境会促使学生有意识地选取第三个干扰项“无法计算”.

阶段（四）：实施

当数学模型构建成功后，还需根据实际试题的具体语境，应用特定方法得出试题的解决方案.本实施阶段主要包括寻找计算周期和准确完成计算过程.那么，在本阶段哪里会发生错误呢？例如，有的学生忽视题干中的提示信息，给出如下实施过程：41003=22006（有选择地把“求41003最后两位数字”的问题转化为“求22006最后两位数字”的问题）=22+21×95×29（计算依据：除第一项21外，后面项的最后两位数字重复的周期是20，如22和222最后两位数字都是04，所以，仅计算最后两位数字得）=04× 512=2048，就会有第四个干扰项48.

综上所述，笔者设计出如下问题选项：

4　总结

综上，笔者有这样的观点：数学教师如果理解并掌握住侧重于描述学生在问题解决过程中认知经历的思维模式（解读→表征→构建→实施），则可将该思维模式应用于数学选择题中干扰项的编制上，借此可揭示出学生在问题解决过程中每个认知阶段的根本性错误，以此来提升数学教师的测试题编制能力.另外，该思维模式可为数学选择题这个范畴的测试题编制提供统一标准，以此保证数学教师编制的数学选择题在测试时能得到一致的反馈结果，体现公平性和有效性.

［1］张奠宙，宋乃庆.数学教育概论（第二版）［M］.北京：高等教育出版社，2009.

［2］约翰·杜威.我们如何思维［M］.伍中友，译.北京：新华出版社，2010.

［3］华莱士.思想的艺术［M］.北京：中华书局，2003.

［4］波利亚.怎样解题：数学思维的新方法［M］.徐泓，冯承天，译.上海：上海科技教育出版社，2007.

［5］朱德全.数学问题系统的构建与解决程式［J］.中国教育学刊，1999（5），10：41-44.

［6］蔡燊安，李祝华.创造的生理心理机制及社会最优化［J］.江西社会科学，1984（1）：115-122.

［7］吴鸿业.用口述分析法研究大、中、小学生问题解决的基本思维过程［J］.心理科学通讯，1988（3）：47-49.

［8］SILVER E，MAMONA-DOWNS J，LEUNG S，et al.Posing mathematical problems：An exploratory study［J］.Journal for Research in Mathematics Education，1996,27（3）：293-309.

An Inquiry of Compilation of Mathematic Choice Question Based on Cognitive Process Analysis

ZHANG Lei
（School of Mathematics&Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

In this paper，by means of case study，we first put forward a thinking model which focuses on describing cognitive experience of the student in the process of solving questions：interpretation→representation→construction→implement.Then，in order to promote mathematics teacher’s capability of compiling quiz question，the author applies the thinking model to the compilation of disturbance term in mathematic choice question，whereby mathematics teacher can uncover the essential mistake in every cognitive stage of the student during the problem-solving process.In addition，the thinking model can provide a single standard for the quiz compilation pertaining to the category of mathematics choice question，for ensuring that the mathematic choice question compiled by mathematics teacher can get a consistent feedback in test.

problem solving；cognition；thinking mode；mathematics choice question；disturbance term

G 427

A

1007-6883（2016）03-0095-06

责任编辑朱本华

2015-12-07

韩山师范学院2015年度教学改革项目（项目编号：HJG1524）.

张磊（1981-），男，河南确山人，韩山师范学院数学与统计学院讲师.