约束条件为取大-取小型模糊关系不等式的取小-取大规划问题

林海涛，杨晓鹏

（韩山师范学院数学与统计学院，广东潮州　521041）

约束条件为取大-取小型模糊关系不等式的取小-取大规划问题

林海涛，杨晓鹏

（韩山师范学院数学与统计学院，广东潮州521041）

提出了目标函数为取小-取大规划、约束条件为取大-取小型模糊关系不等式的优化规划模型.通过求解其导出的单变量模糊关系不等式，得到求解该优化模型的一种简易算法.同时讨论了该规划模型解的存在性、解的结构及最优解的唯一性的等价条件.最后给出两个数值例子.

取小-取大规划；取大-取小型模糊不等式；导出的单变量模糊关系不等式

取大-取小合成算子是模糊数学的基本运算.自从法国模糊学家、生物数学家桑切斯（E.Sanchez）［1，2］在1972年第一次提出了含取大-取小合成算子的模糊关系方程并进行开创性的探究之后，模糊关系方程开始被应用于多个领域，诸如模糊逻辑推理、人工智能、模糊决策和图像处理.模糊关系方程的研究主要有两个方向：研究解的算法和结构；研究模糊关系方程约束的规划问题.曹炳元在文献［3］中详细介绍了取大-取小模糊方程的求法，B.S.Shieh［4-5］讨论了取大-取小合成算子的模糊关系方程的新的求法.同时，具有模糊关系方程约束的规划问题也成了研究的热点.杨吉会、曹炳元［6］应用惩罚函数和遗传算法提出了具有模糊关系约束的线性规划的一种解法.最近几年，他们在文献［7-9］中提出了模糊关系的几何规划及其解法.Cheung-Wen Chang［10］解决了目标函数为加权求和、约束条件为取大-取小模糊关系方程的优化问题.本文将探讨目标函数为取小-取大、约束条件为取大-取小模糊关系不等式的优化问题.

1　预备知识

定义1取大-取小型模糊不等式是指型如

的方程.式中aij,bi,xj∈［0,1］，i∈I=｛1,2,…,m｝，j∈J=｛1,2,…,n｝，I,J是两个指标集.不等式组（1）可以记为 （ai1∧x1）∨（ai2∧x2）∨…∨（ain∧xn）≥bi， i∈I.或 A∘x≥b，其中 A=（aij）m×n，b=（bi）m×1，x=（xj）n×1.

定义2称不等式组（1）是相容的，如果（1）有可行解.即存在x∈［0,1］n，使得A∘x≥b成立.并记（1）的所有可行解的集合为X（A,b）=｛x|A∘x≥b｝.

证明（必要性）若式（1）是相容的，即存在，使得

记式（1）的极小解集为X̆（A,b）.定理2可以看出式（1）的解集由其唯一的最大解和有限个极小解完全决定.

定理2［3］式（1）是相容的，则（1）的所有解集为

根据定理2，当式（1）相容时，它的解集X（A,b）是一个非凸集.为了求式（1）的解集，一般要求出其最大解和全部极小解.前面讨论知最大解为=［1,1,...,1］T，而对于极小解的求解，一般比较困难.

2　模型建立

建立如下的数学规划模型

模型（2）是含取小-取大目标函数且约束条件为取大-取小模糊不等式方程的非凸优化问题.本文的目标就是求出模型（2）的最优解.为了求得模型（2）的最优解，引入“导出模糊关系不等式”的定义.

定义4设变量t∈［0,1］，称

为模糊关系不等式（1）的导出模糊关系不等式，其中aij,bi为（1）所定义.

并记下面模型为（4）

可见，模型（4）为单变量的模糊关系不等式.将通过求解模型（4）来求解模型（2）.

3　模型求解

3.1模型（4）求解

证明充分性是显然的，下证必要性.

另一方面，设y为（3）任一可行解，下证：对任意的i∈I，y≥bi，从而，即为（4）的最优解.

（反证法）设存在某一i0，y＜bi0，从而

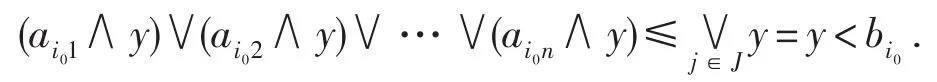
此说明y不是（3）的可行解，与假设矛盾！因而对任意的i，y≥bi，从而.这说明为（4）的最优解.

3.2模型（2）求解

其次，对于（2）的任一最优解y*=［y1,y2,...,yn］T，下证g（y*）≥g（x*）.

（反证法）设g（y*）＜g（x*），即.取，，则，容易验证yˉ为（3）的解.事实上，因为y*=［y1,y2,...,yn］T为（2）之最优解，因而满足（1），即

另一方面，

根据定理3、4，得到求解模型（2）的一种算法

证明根据定理4的证明，可知x*为模型（2）的最大最优解.设模型（2）的任意最优解为x=（x1,x2,...,x）.一方面，由定理2关于约束条件（1）极小解的结构可知，存在∈X̆（A,b），使得nx≥.另一方面，x必须满足

最后，讨论模型（2）解的唯一性.定理5说明模型（2）的解集一般不唯一，但定理6将给出模型（2）解唯一的充要条件.

定理6模型（2）的有唯一最优解的充要条件是满足：对任意 j∈J，存在i0∈I，使得

由唯一性，x#从而不是模型（2）的最优解，从而不满足（1）.故至少存在某一i0∈I，使得

（充分性）设［x1,x2,...,xn］T为模型（2）任一解，若对任意 j∈J，存在i0∈I，使得

另一方面，由定理5知x*为最大最优解，故从而［x1,x2,...,xn］T=x*，即模型（2）的最优解唯一.

4　数值例子

例1求解优化模型

其中，

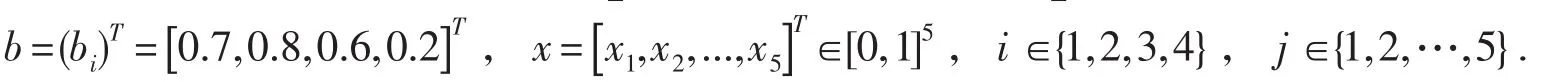
因而，该模型的一个最优解为（0.8,0.8,0.8,0.8,0.8），其最小值为0.8.

例2求解优化模型

解：由本文算法，易求得模型的最小值为g（x）=0.7.同时根据定理6的判别，可知该最优解x*=［0.7,0.7］T为唯一最优解.

5　小结

本文讨论了目标函数为取小-取大规划、约束条件为取大-取小型模糊不等式规划问题（2）.为求解该问题，引入“导出单变量模糊关系不等式”模型（4）.该模型与（2）具有相同的系数.接着讨论了两模型的关系（定理4），并得到模型（2）最优解算法.该算法避开了传统求解所有极小解的复杂的步骤，间接通过计算模型（4）的最优解来获得模型（2）的一个最优解.同时定理5给出模型（2）的解的结构.定理6则给出模型（2）解的唯一性判别的等价条件.最后通过两个数值例子说明了算法的有效性和简易性.该规划可用于实验室点对点网络系统［11］的优化问题，具有一定的现实意义.

［1］SANCHEZ E.Equations de Relations Floues［M］.Marseille：These Biologie Humaine，1972.

［2］SANCHEZ E.Resolution of composite fuzzy relation equations［J］.Information and Control，1976，30：38-48.

［3］曹炳元.应用模糊数学与系统［M］.北京：科学出版社，2005.

［4］SHIEH B S.Solutions of fuzzy relation equations based on continuous t-norms［J］.Inform.Sci.2007，177：4208-4215.

［5］SHIEH B S.New resolution of finite fuzzy relation equations with max-min composition［J］.Int.J.Uncertainty，Fuzziness Knowledge-Based Syst.2008，16（1）：19-33.

［6］杨吉会，曹炳元.具有模糊关系约束的线性规划的解法［J］.系统工程学报，2008，23（5）：627-631.

［7］YANG Jihui，CAO Bingyuan.Geometric programming with fuzzy relation equation constraints［C］//Proceedings of IEEE International Conference on Fuzzy Systems，2005：557-560.

［8］YANG Jihui，CAO Bingyuan.Monomial geometric programming with fuzzy relation equation constraints［J］.Fuzzy Decision Making and Optimization，2007，6（4）：337-349.

［9］CAO Bingyuan.Optimal Models and Methods with Fuzzy Quantities［M］.Berlin Heidelberg：Springer-Verlag：2010.

［10］Cheung-Wen Chang.Linear optimization problem constrained by fuzzy max-min relation equations［J］.Information Sciences 2013，234：71-79.

［11］杨晓鹏，杨晓斌.模糊关系方程在实验室点对点网络系统中的应用［J］.辽宁工程技术大学学报：自然科学版，2016，35（1）：81-84.

Min-max Programming Problem Subject to Max-min Fuzzy Relation Inequalities

LIN Hai-tao，YANG Xiao-peng
（School of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong，521041）

Min-max programming problem subject to max-min relation inequalities is introduced in this paper.The problem is solved with the help of the derived single variable fuzzy inequalities，which has close relationship with the proposed problem.An algorithm for the problem is provided with two numerical examples. Furthermore，the existence，the structure and the uniqueness of the solution to the problem are discussed in the paper.

min-max programming；max-min fuzzy relation inequalities；derived single variable fuzzy inequalities

O 159

A

1007-6883（2016）03-0029-05

责任编辑朱本华

2015-12-31

林海涛（1982-），男，广东揭阳人，韩山师范学院数学与统计学院讲师.