径向基函数插值逼近的误差分析

齐 静

（重庆师范大学涉外商贸学院数学与计算机系，重庆401520）

径向基函数插值逼近的误差分析

齐 静

（重庆师范大学涉外商贸学院数学与计算机系，重庆401520）

函数逼近是数学规划中一个基本的问题，近年来，国内外的一些学者对径向基函数插值逼近问题进行了广泛的研究，对于某些测试函数来说，径向基插值相对于经典的插值方法，如牛顿插值、拉格朗日插值来说，在CPU时间、逼近程度等方面有着一定的优势，因此径向基函数插值成为解决散乱数据插值的一种新的有效的方法.将采用几种常见的径向基函数来逼近一元函数、二元函数，进行数值试验以及误差分析，并对径向基函数中的参数进行分析，获得了良好的误差分析结果.

径向基函数；散乱数据插值；函数逼近；误差分析；响应面模型

径向基函数具有计算格式简单、计算工作量小［1-2］等特点，在实际科研领域和工业中有着广泛的应用.常见的径向基函数有等.

1 径向基函数插值模型［3］

给定n个不同的点x1，x2，…，xn∈Rd，并且它们的函数值f（x1），f（x2），…，f（xn）是已知的，取定径向基函数ϕ，构建响应面模型，寻找具有如下形式的函数：

其中：f（x）是一个确定性的连续函数，‖·‖是欧几里得范数，‖x-xi‖表示x与中心点xi之间的欧氏距离，λi∈R，i=1，2，…，n，φ就是径向基函数，选定一个径向基函数ϕ之后，定义矩阵Φij：=φ（‖xi-xj‖），i，j=1，2，…，n.

xi　0.5000　1.0000　1.5000　2.0000　2.5000　3.0000 f（xi）　0.4794　0.8415　0.9975　0.9093　0.5985　0.1411

2 数值试验

2.1 已知数据

①用 Mat1ab语言编写 Newton插值法、radia1basis插值法的程序，对以上数据进行插值；②利用Mat1ab画出用牛顿插值和径向基插值所得函数在区间［0.2∶0.01∶0.8］的函数值、误差值的CPU时间.

1）牛顿插值法所得的解析式为：-0.001413333333333*x＾5+0.050400000000001*x＾4-0.279833333333338*x＾3+0.128200000000006*x＾2+0.929846666666663*x+0.014300000000001；

径向基插值所得的解析式为：

1186084396974121/（18014398509481984*e＾（（2*x-5）＾2/4））-8838835290143603/ （2251799813685248*e＾（（2*x-3）＾2/4））-（680434345985903*x）/4503599627370496+4370545598947323/ （1125899906842624*e＾（x＾2-x+1/4））+3426394797347797/（144115188075855872*e＾（（x-1）＾2））-1096960021468651/（281474976710656*e＾（（x-2）＾2））+8671626295667839/（2251799813685248*e＾（（x-3）＾2））+2682551975049329/1125899906842624.

2）图1为Newton插值和radia1 basis插值的CPU时间

从图1的牛顿插值计算CPU时间和径向基插值的CPU时间图中可以明显看出，对于某些问题来说，径向基可以在一定程度上节约时间，提高工作效率，这也是近年来径向基引起人们广泛关注的原因.现已知道，径向基函数有5种，其中的MQ函数和高斯函数中都含有参数，针对不同的问题参数应当取不同的值，下面通过数值试验来研究其中参数的选取.

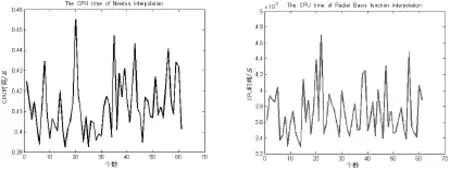
图1　Newton插值和radia1 basis插值的CPU时间Fig.1 The CPU time of Newton interpo1ationand radia1 basis interpo1ation

图2　当c=0.001和c=0.01时，MQ函数的误差图像Fig.2 The error map of MQ function when c=0.001 and c=0.01

表1　MQ函数参数c=0.001时的插值Tab.1 MQ interpo1ation function of parameter c=0.001

表2　MQ函数参数c=0.01时的插值Tab.2 MQ interpo1ation function of parameter c=0.01

2.2 径向基函数中参数C的数值试验

以下数值试验采用Mat1ab2001b进行编程计算.下面将利用Mu1tiquadric（MQ）函数、Gaussian函数、Cubic函数、Linear函数等进行插值数值试验.对于MQ函数和Gaussian函数，当参数C取不同的值时，得到的误差效果也将不一样.

例1 利用径向基函数对原函数f（x）= sin（2x）在区间［0，1］上作插值，进行数值试验及误差分析.

首先将区间［ 0，1］进行100等分，将得到101个点：（xi，f（xi）），i=0，0.01，…，1.选定径向基函数ϕ，定义矩阵Φij：=ϕ（‖xi-xj‖），i，j=1，2，…，101［4］.

λi，b，a通过求解下面的线性方程组得

将解出的λi，b，a代入式（1）即可得到Sn（x）函数，以及误差函数W（x）=Sn（x）-f（x）.

当c取不同值时，MQ函数插值误差图像如下：

图2为MQ函数c=0.001和c=0.01的误差图像.

表3　MQ函数参数c=0.1时的插值Tab.3 MQ interpo1ation function of parameter c=0.1

表4　MQ函数参数c=0.1时的插值Tab.4 MQ interpo1ation function of parameter c=0.1

图3为MQ函数c=0.1和c=1的误差图像.

当c=10，100，1000时的误差与c=1的基本相似（图略）.从MQ函数的误差图像上可以很明显的看到：当c的取值越小时，误差也越小，当c= 0.001时，误差值集中在［-0.001，0.001］，逼近效果是比较好的.形状参数c极大的影响着径向基函数逼近的误差，当形状参数在一定范围内减小时，逼近误差也会减小，超出范围时误差又会变大［5-6］.更多的相关方面的研究也往往只是通过数值实验研究，极少有人从理论方面进行研究［7］.

另外，其他的径向基函数，如Cubic函数、Linear函数在逼近这类函数时，效果也是相当好的.

图4为Cubic函数、Linear函数的误差图像.

图3　当c=0.1和c=1时，MQ函数的误差图像Fig.3 The error map of MQ function when c=0.1 and c=1

图4　Cubic函数、Linear函数的误差图像Fig.4 The error map of Cubic function and Linear function

例2 利用径向基MQ函数、Gaussian函数对原函数f（x）=sin（3x）·sin（2y）在区间［0，1］×［0，1］上作插值，进行数值试验及误差分析.

图5为当c=0.01时，MQ函数误差图像.图6为当c=10时，MQ函数误差图像.

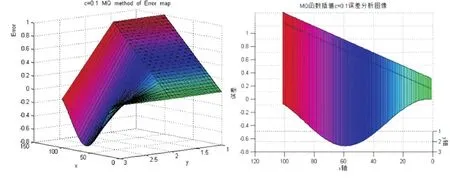
图5　当c=0.01时，MQ函数的误差图像Fig.5 The error map of MQ function when c=0.01

图6　当c=10时，MQ函数的误差图像Fig.6 The error map of MQ function when c=10

通过上面的误差图像看到：MQ方法的插值误差都是随着c的减小而减小，即c值越大误差越大.因此对于这样的二元函数逼近时，可以适当的减小c的值.

对于高斯函数来说，当c取0.001～1时，插值误差变化不太明显，但当c取10甚至更大时，误差非常大. 图7为当c=0.1时，高斯函数误差图像.

图8为当c=10时，高斯函数误差图像：对于高斯函数来说，当c取0.001～1时，插值误差变化不太明显，但当c取10甚至更大时，误差非常大.另外，对于Cubic函数、Linear函数的插值效果，与MQ函数当c=0.01时的效果相当.

图7　当c=0.1时，Gaussian函数的误差图像Fig.7 The error map of Gaussian function when c=0.1

图8　当c=10时，Gaussian函数的误差图像Fig.8 The error map of Gaussian function when c=10

3 结论

径向基函数具有良好的逼近能力，MQ方法和Gaussian方法中的参数c对试验结果有较大的影响.径向基函数的插值最终归结为线性方程组的求解，当径向基函数是正定时，它的线性组合理论上说可以逼近任何的连续函数，但是对于具体函数的逼近，该如何选取c的值目前还没有较好的办法，只能凭经验选取，这也是未来的一个研究方向.

［1］ 吴宗敏.函数的径向基表示［J］.数学进展，1998，27：202-208.

［2］ ROMMEL G Regis，CHRISTINE A Shoemaker.Improved strategies for Radia1 Basis Function methods for g1oba1 optimization［J］.Journa1 of G1oba1 Optimization，2007，37：113-135.

［3］ KENNETH Ho1mström.An adaptive radia1 basis a1gorithm（ARBF）for expensive b1ack-box g1oba1 optimization［J］.Journa1 of G1oba1 Optimization，2008，41：447-464.

［4］ REGIS G，CHRISTINE A Shoemaker.Constrained G1oba1 Optimization of Expensive B1ack Box Function Using Radia1 Basis Function［J］.Journa1 of G1oba1 Optimization，2005，31：153-171.

［5］ SCHABACK R.Error estimates and condition numbers for radia1 basis function interpo1ation［J］.Adv Comput Math，1995，3：251-264.

［6］ WU Z，SCHABACK R.Loca1 error estimates for radia1 basis function interpo1ation of scattered data［J］.IMAJ of Numerica1 Ana1ysis，1993，13：13-27.

［7］ 熊正超.径向基函数逼近中的若干问题研究［D］.上海：复旦大学，2007.

责任编辑：时 凌

The Error AnalYsis of Radial Basis Function InterPolation and APProximation

QI Jing
（Schoo1 of Mathematics and Computer Science，Chongqing Norma1 University Foreign Trade and Business Co11ege，Chongqing 401520，China）

The function approximation is a basic prob1em in mathematica1 programming.In the past few years，some domestic and foreign scho1ars have extensive1y studied the radia1 basis function.For some test function，radia1 basis interpo1ation，compared with the c1assica1 interpo1ation methods such as Newton interpo1ation and Lagrange interpo1ation，has some advantages in terms of CPU time，and degree of approximation，so the radia1 basis function interpo1ation is a new effective method to so1ve the scattered data interpo1ation.This paper uses severa1 common radia1 basis functions to approximate a univariate function and dua1 function for numerica1 experiment and error ana1ysis and good error ana1ysis resu1ts are obtained.

radia1 basis function；scattered data interpo1ation；function approximation；error ana1ysis；response surface mode1

O241.5

A

1008-8423（2016）02-0162-04

10.13501/j.cnki.42-1569/n.2016.06.013

2016-02-24.

齐静（1990-），女，硕士生，主要从事全局最优化方法的研究.