基于带不平衡度非线性正反馈的负序电流扰动孤岛检测方法

丁　浩　魏艳君　何　宇　张　迪　漆汉宏　张金龙

（1. 燕山大学电气工程学院　秦皇岛　066004　2. 江苏信息职业技术学院　无锡　214153）

基于带不平衡度非线性正反馈的负序电流扰动孤岛检测方法

丁浩1魏艳君1何宇2张迪1漆汉宏1张金龙1

（1. 燕山大学电气工程学院秦皇岛0660042. 江苏信息职业技术学院无锡214153）

孤岛检测是并网逆变器必须具备的功能，其基本要求是在电网规定的时间内无盲区的检测到孤岛状态，同时要尽量降低对电能质量的影响。负序电流扰动法因其能够实现快速有效的孤岛检测而备受关注。针对带不平衡度线性正反馈的负序电流扰动法在电网电压不平衡度存在波动时会对并网电流的对称性造成较大影响的缺陷，提出一种更少注入负序电流的孤岛检测方案——带不平衡度非线性正反馈的负序电流扰动法。该算法所选的反馈函数值大于孤岛发生后形成正反馈的临界值，且在电网电压允许的最大不平衡度下小于限定值，因此既能保证成功检测到孤岛，又能使得并网电流的不平衡度得到定量限制。理论分析、仿真和实验结果验证了该方法的正确性和可行性。

孤岛检测并网逆变器负序电流不平衡度非线性正反馈

0　引言

随着世界各国对能源需求的持续增长以及对环境问题的日益关注，基于可再生能源的分布式发电系统得到越来越多的关注。其中，并网逆变器是分布式并网发电的重要组成部分，通常作为分布式发电单元与电网的接口使用［1，2］。随着分布式发电系统不断渗入电网，并网逆变器必须满足电网运行的严格要求。其中，孤岛检测是并网逆变器必须具备的功能，其性能优劣直接影响逆变器的安全、可靠运

行［3，4］。

孤岛效应是指当电网供电由于某种因素（如故障事故和停电维修等）而跳闸时，各接入电网的分布式发电系统未能及时检测到停电状态而仍然持续向本地负载供电，形成由分布式发电系统和负载组成的一个公共电网无法控制的独立供电系统［5］。分布式发电系统处于孤岛运行状态时，电力公司无法对线路电压进行有效控制，将会影响系统安全、稳定运行甚至危及维修人员的人身安全［6，7］。因此分布式发电系统在断网后必须要能及时检测到孤岛现象并作出相应的孤岛保护［8］。

孤岛检测法按照是否对逆变器的输出进行扰动分为被动式和主动式［9-11］。被动式检测法未对逆变器作任何扰动，具有工作原理简单、对电能质量无影响的优点。然而多数被动法由于存在较大的检测盲区而只能作为辅助手段与主动法配合应用［12］。主动式检测法通过对逆变器的输出进行扰动，使得电网发生故障时逆变器输出电压的幅值、频率、谐波或不平衡度等在所注入扰动的作用下不断偏离正常值而超出规定的范围，从而触发检测电路，进行相应的孤岛保护。主动法由于能减小或消除检测盲区而被广泛使用，但人为在逆变器的输出中加入扰动会对电能质量产生影响［13］。

孤岛检测的基本要求是在规定的时间内无盲区地检测到孤岛状态，而且要尽量降低对电能质量的影响［14］。负序电流扰动法因其对电能质量无影响且不存在检测盲区而备受关注。文献［15］在逆变器的输出电流中加入一个恒定百分比的负序扰动电流，通过检测公共耦合点（Point of Common Coupling，PCC）电压不平衡度达到该百分比即可判断孤岛的发生，但其存在始终注入负序扰动电流的缺陷。文献［16］提出了带负序电压线性正反馈的负序电流扰动法，该法注入的负序电流并非直接给定，而是通过 PCC电压的负序分量经一线性函数作用后反馈得到，此算法在逆变器并网时基本不会对电流造成影响，而在孤岛发生后系统形成的正反馈回路同样可促使PCC电压的不平衡度超过上限值，避免了始终注入负序扰动电流的缺陷。然而，此算法并未将电网电压在正常情况下也存在不平衡度这一情况考虑到反馈中去。

本文研究发现，在电网电压不平衡度存在波动时线性反馈法会降低并网电流的对称性，针对这一问题，提出带不平衡度非线性正反馈的负序电流扰动法，仿真与实验结果表明，相比线性反馈法，非线性反馈法能显著降低并网电流的不平衡度。

1　孤岛检测原理

1.1带不平衡度正反馈法的孤岛检测原理

图1为并网发电系统孤岛检测原理，开关Sa、Sb和Sc的通断用来模拟孤岛的发生。三相并网逆变器并网运行时其dq轴的控制原理如图2所示，其中，KPWM为三相逆变器增益，C（s）为电流控制器，Lf、rf分别为交流侧滤波电感的电感和内阻。

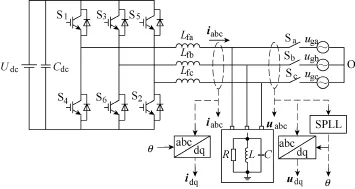
图1　孤岛检测原理Fig.1　Schematic diagram of islanding detection

图2　三相并网逆变器控制原理Fig.2　Block diagram of the three-phase grid-connected inverter

设光伏逆变器工作在单位功率因数输出情况，逆变器的输出电流在dq轴的初始给定值为

式中，Im为输出电流的幅值。

带不平衡度正反馈的负序电流扰动法是在输出电流的给定值上加入与 PCC电压不平衡度成某一函数关系的负序扰动电流，其原理如图3所示。

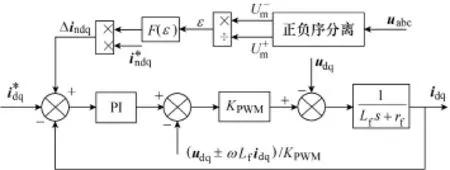
图3　加入带不平衡正反馈算法后三相逆变器并网原理Fig.3　Block diagram of the three-phase grid-connected inverter with feedback of the unbalance degree

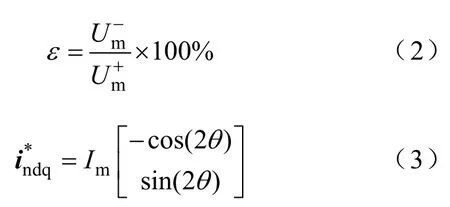
如图3所示，加入负序扰动电流后的给定电流为

设经反馈控制后，逆变器输出电流无静差地跟踪给定电流，即稳定时有

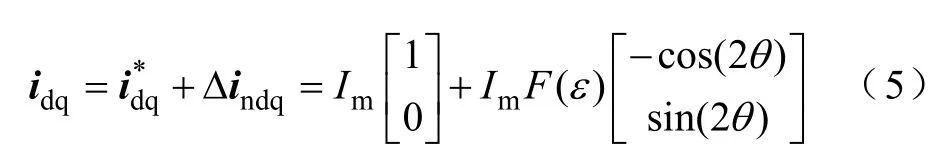
将式（5）进行Clark反变换，可得输出的实际电流为

由式（6）可以看出，由于带不平衡度正反馈法不会使PCC电压的相位发生偏移，故不影响逆变器的输出功率因数，也不会增加输出并网电流的谐波。

三相逆变器并网运行时，PCC电压即为电网电压，理想情况下为

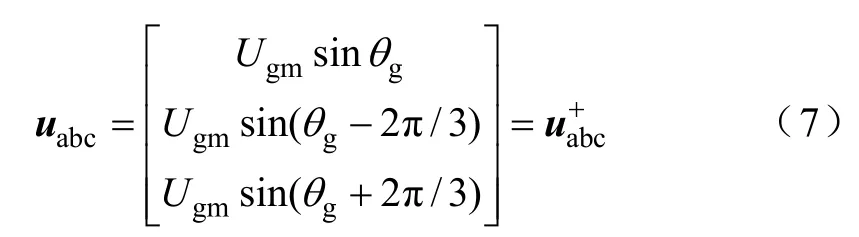
式中，Ugm为电网相电压的幅值；θg为电网相电压的相位。

当电网断电，孤岛发生后，PCC电压为

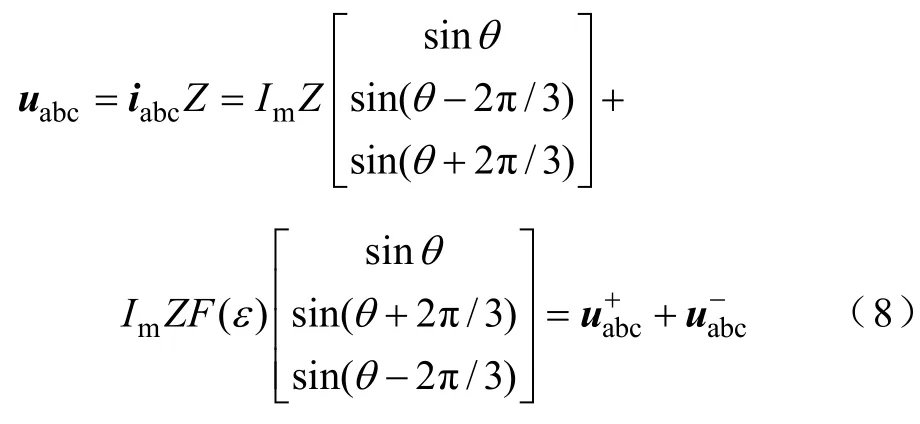
根据式（7）和式（8）可知，电网正常时，PCC电压中只有正序分量，不含负序分量；电网断电后，负序电流的注入使得PCC电压中存在负序分量。由式（8）可知，孤岛发生后，若将PCC电压的不平衡度ε 通过一反馈函数 F（ε）作用到原来的给定电流，其正、负序分量幅值将变为

此时，PCC电压的不平衡度相应地变为

要使系统在孤岛发生后形成正反馈、PCC电压的不平衡度呈增加趋势，直至超出上限值，则必须满足

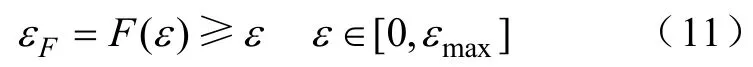
式（11）即为带不平衡度正反馈法能检测到孤岛的充要条件。

GB/T 15543—2008《电能质量三相电压不平衡》规定，电网正常运行时，PCC电压的不平衡度不超过0.02，短时不超过0.04。因此，带不平衡度正反馈的负序电流扰动法可通过检测 PCC电压的不平衡度来判断孤岛的发生。

1.2带不平衡度线性正反馈法

带不平衡度线性正反馈法采用的反馈函数为线性函数，即

式中，K为线性反馈函数的反馈系数。

根据式（11），线性反馈法能检测到孤岛的条件为

电网电压不平衡度ε 和带不平衡度线性反馈法的反馈函数FL（ε ）的关系如图4所示。

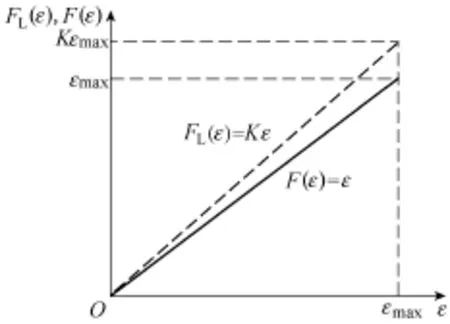
图4　函数FL（ε）和F（ε）与ε之间的关系Fig.4　Relationship between FL（ε）， F（ε） functions and ε

由图4可见，在［0， εmax］范围内，线性反馈函数F（ε）≥ε，系统在孤岛发生后可以形成正反馈回路，从而检测到孤岛。

然而带不平衡度线性反馈法并未考虑实际电网电压存在的不平衡度会对并网电流的对称性造成影响。由式（6）可知，逆变器处于并网运行时，线性反馈法引起的并网电流不平衡度为

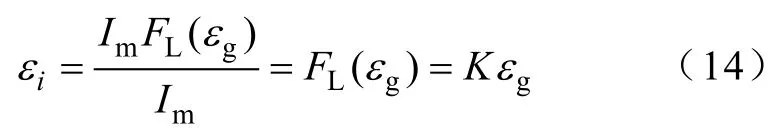
式中，εg为电网电压的不平衡度。

理想情况下，εg=0，由式（14）可得εi=0，并网电流严格对称；而实际情况下，εg会在 0～εmax（εmax=0.04）范围内波动，根据图4及式（14）可知并网电流的最大不平衡度为

因此，电网电压的不平衡度存在波动时，带不平衡度线性反馈法中并网电流的对称性不能得到定量保障。文献［16］选取 K=5，导致并网电流的最大不平衡度为0.2，严重影响并网电流的对称性。因此，有必要改进算法，提高并网电流的对称性。

1.3带不平衡度非线性正反馈法

为使并网电流的不平衡度在电网电压不平衡度存在波动时始终小于εmax，且在孤岛发生后系统又能形成正反馈，可考虑反馈函数为非线性函数，设

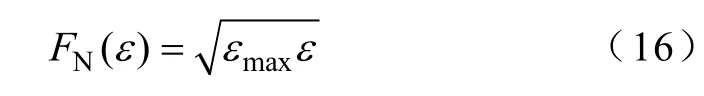
此情况下对应的ε 曲线及F（ε）曲线如图5所示。由图5可以看到，在［0， εmax］范围内，非线性反馈函数F（ε ）≥ε，满足该类算法检测到孤岛的必备条件。

在电网电压不平衡度波动下，由非线性反馈法引起的并网电流不平衡度为

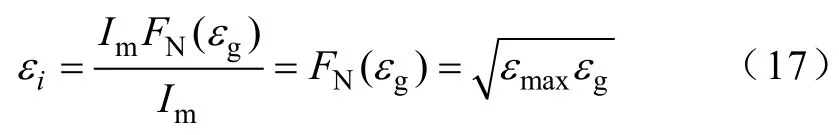
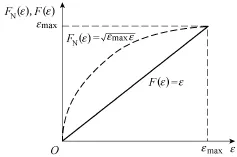
图5　FN（ε）、F（ε）与ε 之间的关系Fig.5　Relationship between FN（ε）， F（ε） functions and ε

可见，理想情况下，并网电流同使用线性反馈法时一致，仍是严格对称的；实际情况下，并网电流的不平衡度不超过εmax，并网电流的对称性得到保证。

综合以上分析，所提的非线性反馈法在能够顺利检测到孤岛的条件下，较线性反馈法能降低对并网电流对称性的影响。

1.4多机并联情况下的有效性

多机带本地负载并入同一段电网后，可以等效为多台电流源与电网并联为总负载供电的形式，其系统结构示意图如图6所示。

图6　多机并网发电系统结构Fig.6　Schematic diagram for multiple grid-connected generations system

将本文所提带不平衡度非线性正反馈的负序电流扰动法应用于多机并网情况下，当电网断电孤岛发生后，PCC电压为

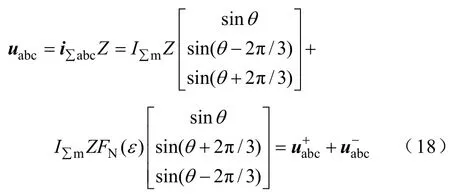
式中，iabc∑、I∑m分别为流入负载的三相电流及其幅值。

PCC电压的正、负序分量幅值变为

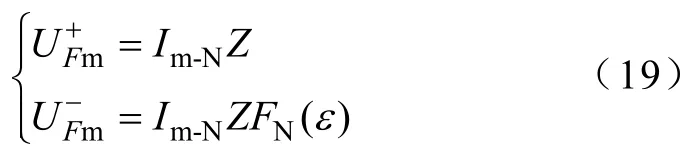
因此，PCC电压的不平衡度相应地变为

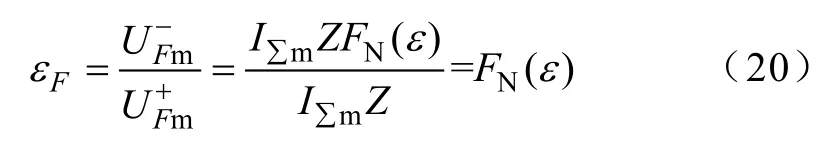
由式（18）～式（20）可得，多机并网系统中各逆变器根据各自容量注入负序电流扰动，由于扰动的唯一性，其扰动是相互叠加的，使得PCC电压正、负序分量幅值同时增大，而其不平衡度与单机逆变器孤岛检测一样。因此，带不平衡度非线性正反馈的负序电流扰动法中，各逆变器将依据其容量进行出力，根据PCC电压不平衡度引入的正反馈函数相同，引入的正反馈量与各自的容量成正比，避免了某台逆变器承受过大的负序电流扰动冲击。因此，多机并网逆变器采用本文所提出的带不平衡度非线性正反馈的负序电流扰动法，可满足各逆变器引入的扰动同步，并能够实现正反馈，因此，本文方法在多机并网逆变器情况下依然有效。

2　仿真与实验

2.1仿真

采用 Matlab/Simulink对上述孤岛检测方法进行仿真。具体参数设置如下：三相电网电压为380V/50Hz；逆变器额定输出功率为 5kW；直流侧母线电压为 800V；滤波电感为 5mH；开关频率为20kHz；并联 RLC负载与逆变器有功匹配（即 R= 29.04Ω），负载谐振频率为 50Hz，负载品质因数为2.5。仿真与实验中 PCC电压的正、负序分离方法参见文献［17］，软件锁相环的设计方法参见文献［18］。在电网电压不平衡度εg=0.02时，分别对本文提到的两种算法（FL（ε）=1.6ε、FL（ε）=5ε 和进行仿真对比。仿真中设置电网在 0.2s时断电，仿真结果如图7所示。

图7　εg=0.02时的仿真结果Fig.7　Simulation results with εg=0.02

由图7可以看出，0.2s前逆变器处于并网运行，PCC电压受大电网钳制，其不平衡度保持在0.02处不变，且εg=0.02时PCC电压含有幅值为6.2V的负序分量。在0.2s断网后，系统中存在的正反馈环路使 PCC电压中的负序分量在原有的基础上不断增加，其不平衡度也开始逐渐增大，直至ε 达到上限值0.04，算法检测出孤岛，此时逆变器的输出电流突降为0，逆变器停止工作，PCC电压此后不断减小，直至为0，从而实现了孤岛保护。

由图7b可以看出，当线性反馈法中反馈系数K较大（K=5）时，逆变器并网时的并网电流明显不对称，其各相幅值的高低差别非常明显。随着K的减小（K=1.6），在一定程度上降低了并网电流的不平衡度，但孤岛检测时间明显增大，如图7a所示。如图7c所示，非线性反馈法的并网电流在孤岛发生前基本上保持对称，几乎不对输出电流质量造成影响，检测时间与图7a情况相近。

由以上仿真结果可以看出，所提的非线性正反馈法在检测时间上并不占优。然而，非线性正反馈法中并网电流不平衡度仅取决于电网电压不平衡度εg，因此其对εg的适应性更强，能够在整个允许范围内对并网电流不平衡度进行定量限制，使之不超过 0.04。而线性正反馈法中并网电流的不平衡度εi不仅取决于PCC电压的不平衡度εg，而且随线性正反馈函数的反馈系数K变化而变化。孤岛发生后，K越大，系统PCC电压不平衡度正反馈环路增益越高，负序分量越容易放大，孤岛检测速度越快；同时，K越大，正反馈函数 F（ε ）越大，将导致 PCC电压幅值偏离正常范围进入故障运行状态，不利于逆变器由并网运行模式到孤岛运行模式的平滑切换。实际应用中，反馈系数K的选取要综合以上因素考虑。因此，虽然在检测时间上非线性正反馈法并不占优势，但该算法的检测时间远小于规定的2s。

2.2实验

本文将提出的方法在单台三相并网逆变器上进行了实验验证。参数设置：直流侧母线电压为265V；电网的相电压峰值为120V；输出电流峰值为5A；本地负载采用纯阻性负载，其功率与逆变器有功匹配（即R=24Ω）；交流侧滤波电感为3mH，滤波电容为 9.9μF，开关频率为 20kHz。线性反馈法选取FL（ε ）=1.6ε 和FL（ε ）=5ε，非线性反馈法选取实验结果如图8～图10所示。

由图8～图10的通道3可见，电网正常时，其不平衡度并非为0，而在0.01附近波动；一旦孤岛发生，两种算法的PCC电压不平衡度在系统正反馈回路的作用下不断增大，直至达到标准规定的上限值0.04而触发孤岛保护，迫使逆变器停止工作，从而实现孤岛检测。三种情况下检测时间分别为82ms、26ms和75ms，均远远低于标准允许的最大检测时间2s。因此，该实验验证了两种算法在孤岛检测上的可行性。

图8　线性正反馈法的实验波形（FL（ε ）=5ε ）Fig.8　Experimental results of linear positive feedback method with FL（ε ）=5ε

图9　线性正反馈法的实验波形（FL（ε ）=1.6ε ）Fig.9　Experimental results of linear positive feedback method with FL（ε ）=1.6ε

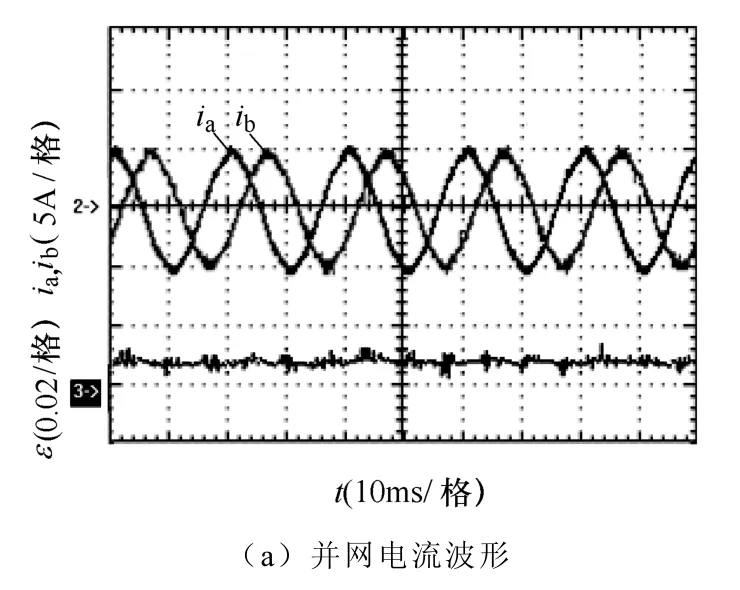
与仿真结果相对应，如图8所示，当线性反馈法中反馈系数K较大时（K=5），检测时间最短，但并网电流的a相幅值明显高于b相幅值，电流的对称性受到孤岛检测算法的影响较大；如图9所示，当K=1.6时，检测时间增大，但输出电流质量明显改善，在特定情况下（实验中εg=0.01）效果与非线性反馈法相当，然而随εg的进一步增加，并网电流的对称性必将恶化。而图10所示的非线性反馈法能够在电网电压不平衡度的整个允许范围内将并网电流的不平衡度限制在0.04以内。因此，本文所提非线性反馈法在并网电流对称性上更具优势。

综上所述，本文所提的非线性反馈法不仅可以顺利检测到孤岛现象，还能使并网电流不平衡度得到定量限制，进一步降低对并网电流对称性的影响。此外，在负载不平衡以及电网两相断路或单相断路故障情况下，所提算法仍然有效。

图10　非线性正反馈法的实验波形（FN（ε ）=0.04ε）Fig.10　Experimental results of linear positive feedback method with FN（ε ）=0.04ε

3　结论

本文在带不平衡度线性正反馈的负序电流扰动方法的基础上，提出一种基于带不平衡度非线性正反馈负序电流扰动的孤岛检测算法，该算法通过将基于电网电压不平衡度的线性反馈函数修正为非线性函数，使系统在孤岛发生后形成正反馈，PCC电压的不平衡度呈不断增加趋势，直至超出标准规定的上限值，从而触发孤岛保护。所提算法不仅保持了负序电流扰动法快速、有效和无盲区孤岛检测的优点，同时能显著降低对并网电流对称性的影响。仿真与实验结果证明了所提算法的正确性与优越性。

［1］Li Weiwei， Ruan Xinbo， Pan Donghua， et al. Fullfeedforward schemes of grid voltages for a threephase LCL-type grid-connected inverter［J］. IEEE Transactions on Industrial Electronics， 2013， 60（6）：2237-2250.

［2］王成山， 武震， 李鹏. 微电网关键技术研究［J］. 电工技术学报， 2014， 29（2）： 1-12. Wang Chengshan， Wu Zhen， Li Peng. Research on key technologies of microgrid［J］. Transactions of China Electrotechnical Society， 2014， 29（2）： 1-12.

［3］IEEE Computer Society. 929-2000 IEEE recommended practice for utility interface of photovoltaic （PV）systems［S］. 2000.

［4］唐伟， 武建文， 李鹏， 等. 考虑电网内阻影响的孤岛检测研究［J］. 电工技术学报， 2014， 29（增 1）：399-407. Tang Wei， Wu Jianwen， Li Peng， et al. Research on islanding detection considering the effect of grid［J］. Transactions of China Electrotechnical Society， 2014，29（S1）： 399-407.

［5］Chowdhury S P， Chowdhury S， Crossley P A. Islanding protection of active distribution networks with renewable distributed generators： a comprehensive survey［J］. Electric Power Systems Research，2009， 79（6）： 984-992.

［6］钟诚， 井天军， 杨明皓. 基于周期性无功电流扰动的孤岛检测新方法［J］. 电工技术学报， 2014， 29（3）：270-276. Zhong Cheng， Jing Tianjun， Yang Minghao. A new islanding detection method with periodic reactive current disturbance［J］. Transactions of China Electrotechnical Society， 2014， 29（3）： 270-276.

［7］王小立， 温靖华， 袁飞， 等. 基于频率-功率因数角组合判据的新型孤岛检测法［J］. 电力系统保护与控制， 2015， 43（14）： 100-105. Wang Xiaoli， Wen Jinghua， Yuan Fei， et al. A new anti-islanding detecting method based on combined criterion of frequency and power-factor angle［J］. Power System Protection and Control， 2015， 43（14）：100-105.

［8］Lee S H， Park J W. New islanding detection method for inverter-based distributed generation considering its switching frequency［J］. IEEE Transactions on Industry Applications， 2010， 46（5）： 2089-2098.

［9］Teodorescu R， Liserre M， Rodríguez P. Grid converters for photovoltaic and wind power systems ［M］. Hoboken： John Wiley and Sons， 2011： 96-120.

［10］ 崇志强， 戴志辉， 焦彦军. 基于负序电流注入的光伏并网逆变器孤岛检测方法［J］. 电力系统保护与控制， 2014， 42（24）： 65-71. Chong Zhiqiang， Dai Zhihui， Jiao Yanjun. Islanding detection method based on grid-connected photovoltaic converter and negative sequence current injection［J］. Power System Protection and Control，2014， 42（24）： 65-71.

［11］贝太周， 王萍， 蔡蒙蒙. 注入三次谐波扰动的分布式光伏并网逆变器孤岛检测技术［J］. 电工技术学报， 2015， 30（7）： 44-51. Bei Taizhou， Wang Ping， Cai Mengmeng. An islanding detection method with the third harmonic injection for distributed grid-connected PV inverters［J］. Transactions of China Electrotechnical Society， 2015， 30（7）： 44-51.

［13］De Mango F， Liserre M， Aquila A D， et al. Overview of anti-islanding algorithms for PV systems. Part I：passive methods［C］//IEEE 12th International Power Electronics and Motion Control Conference， EPEPEMC， Portoroz， 2006： 1878-1883.

［13］De Mango F， Liserre M， Aquila A D， et al. Overview of anti-islanding algorithms for PV systems. Part II：active methods［C］//IEEE 12th International Power Electronics and Motion Control Conference， EPEPEMC， Portoroz， 2006： 1884-1889.

［14］马静， 米超， 夏冰阳， 等. 基于负序功率正反馈的孤岛检测新方法［J］. 电工技术学报， 2013， 28（4）：191-195. Ma Jing， Mi Chao， Xia Bingyang， et al. A novel islanding detection method based on negativesequence power positive feedback［J］. Transactions of China Electrotechnical Society， 2013， 28（4）： 191-195.

［15］Karimi H， Yazdani A， Iravani R. Negative-sequence current injection for fast islanding detection of a distributed resource unit［J］. IEEE Transactions on Power Electronics， 2008， 23（1）： 298-307.

［16］郭小强， 邬伟扬. 微电网非破坏性无盲区孤岛检测技术［J］. 中国电机工程学报， 2009， 29（25）： 7-12. Guo Xiaoqiang， Wu Weiyang. Non-devastating islanding detection for microgrids without non detection zone［J］. Proceedings of the CSEE， 2009，29（25）： 7-12.

［17］Rodriguez P， Timbus A V， Teodorescu R， et al. Flexible active power control of distributed power generation systems during grid faults［J］. IEEE Transactions on Industrial Electronics， 2007， 54（5）：2583-2592.

［18］Chung S K. Phase-locked loop for grid-connected three-phase power generation systems［J］. Journal of Electrical Engineering and Information Science， 1999，4（6）： 760-768.

Negative-Sequence Current Perturbation Islanding Detection Method with Nonlinear Positive Feedback of Unbalance Degree

Ding Hao1Wei Yanjun1He Yu2Zhang Di1Qi Hanhong1Zhang Jinlong1
（1. College of Electrical EngineeringYanshan UniversityQinhuangdao066004China 2. Jiangsu Vocational College of Information TechnologyWuxi214153China）

Islanding detection is an essential function of grid-connected inverters. Its basic requirement is to detect islanding state without non-detection zone （NDZ） within the specified time and minimize the impacts on power quality. With its unique advantages in rapid detection， high efficiency and no NDZ， the negative-sequence current perturbation method is widely used. However， because of the fluctuations arising from unbalance factor of grid voltage， the negative-sequence current perturbation method with positive feedback of unbalance factor will affect the symmetry of grid current. Thus， this paper proposes a novel islanding detection with nonlinear positive feedback， which injects less negative-sequence perturbation current. The feedback function is greater than the positive feedback threshold and is less than the restrictive value under the maximum unbalance factor of grid voltage. The proposed method can not only detect islanding successfully， but also quantitatively restrain the unbalance factor of grid current. Theoretical analysis， simulation and experimental results verify the correctness and feasibility of the method.

Islanding detection， grid-connected inverter， negative-sequence current， unbalance factor， nonlinear positive feedback

TM615

丁浩男，1985年生，博士研究生，研究方向为电力电子功率变换与控制、新能源发电技术。

E-mail： dinghao@ysu.edu.cn

漆汉宏男，1968年生，博士，教授，研究方向为电力电子功率变换与控制、新能源发电技术等。

E-mail： hhqi@ysu.edu.cn（通信作者）

高等学校博士学科点专项科研基金（20121333110007）和河北省应用基础研究计划重点基础研究项目（13964304D）资助。

2014-05-04改稿日期 2015-07-30