基于模块化多电平变换器的静止同步补偿器桥臂不对称及其控制策略

秦海鸿　赵海伟　马策宇　董耀文　聂　新

（南京航空航天大学自动化学院　南京　210016）

基于模块化多电平变换器的静止同步补偿器桥臂不对称及其控制策略

秦海鸿赵海伟马策宇董耀文聂新

（南京航空航天大学自动化学院南京210016）

在高压大容量无功补偿领域，采用模块化多电平变换器（MMC）作为静止同步补偿器（STATCOM）主电路拓扑，目前已经在工程上得到了应用。在模块化多电平变换器上、下桥臂参数不对称时，基频交流分量在上、下桥臂之间分配不均，同时桥臂电流中的直流分量和二倍频分量也会流入交流侧。建立了桥臂参数不对称MMC-STATCOM的交流侧和直流侧模型，分析了不同频率下等效电路中桥臂不对称对稳态电流的影响，提出了抑制基频共模分量及二倍频共模分量并维持上、下桥臂直流电压稳态平衡的控制策略。仿真和实验结果验证了理论分析的正确性和控制策略的有效性。

模块化多电平变换器不对称基频电流二倍频电流模型

0　引言

为了减小器件电压应力以及避免器件的直接串联，多电平拓扑应运而生，被广泛应用于高电压大功率场合［1-3］。其中，中点钳位型和飞跨电容型拓扑很难扩展到更高的电压等级［4］，级联H桥型多电平拓扑需要额外的直流电源对悬浮电容进行充电，降低了系统的功率密度，成本较高。

2003年德国学者 R. Marquardt提出了一种新型多电平变换器［5］——模块化多电平变换器（Modular Multilevel Converter， MMC）。MMC具有高度模块化、易于扩展、可四象限运行及无体积较大的输入变压器等优点，被认为是高压大功率场合最有竞争力的电压源型变换器［6］。近年来，MMC受到了广泛的关注和重视，被广泛应用于高压直流（High-Voltage Direct Current， HVDC）输电［7］、电机驱动［8］、新矩阵变换器［9］等领域。在2009年底，世界上首个采用MMC技术的静止同步补偿器（Static synchronous Compensator， STATCOM）装置在英格兰塔奈特岛风力发电站投入运行［10］，其输出无功功率为±35Mvar。

与传统电压源型变换器相比，MMC变换器子模块直流侧电容是悬浮的，当桥臂电流流经子模块直流侧电容时会引起较大的电压波动，该电压波动可能引起上、下桥臂电压及三相输出电压的不平衡，进一步导致相间低频环流的出现并持续恶化系统。文献［11］推导了电容电压的瞬时表达式，并给出电容值的选取和计算方法。文献［12］对电容电压波动和相间环流进行了数学分析，提出电容电压主要波动成分为基频分量和二倍频分量，内部环流仅包含以二倍频为主的偶次谐波成分。文献［13］提出了三相解耦2次谐波环流抑制算法，该算法首先通过数学分析获得电容电压参考指令，然后将桥臂调制波除以电容电压参考指令从而得到开关管驱动信号。文献［14］采用二倍频负序旋转坐标变换将内部三相环流分解为两个直流分量，并设计了相应的控制器。

尽管现有文献对MMC的数学模型分析和控制策略做了大量的工作，但这些分析大都是基于系统对称和三相参数对称的情形，且用于STATCOM场合的研究较少。文献［15］对交流系统不对称工况进行了分析，指出了桥臂共模电流不仅包含直流分量和偶次谐波环流分量，而且还包含有2次零序谐波分量，导致直流母线电压和电流中出现2次谐波分量。文献［16］对上、下桥臂电压进行了分析，指出上、下桥臂不平衡电压是由两部分构成，一部分不可通过控制策略消除，另一部分可以通过合适的调制策略消除。文献［17］根据电容电压的变化规律，从时域角度列写了桥臂不对称的MMC环流的二阶微分方程，指出环流主要成分为直流分量、基波分量和二倍频分量，但没有对桥臂不对称情况下的控制策略作进一步研究。

针对这一问题，本文首先建立了基于桥臂不对称MMC-STATCOM的数学模型，并根据等效子电路对桥臂电流进行分析，提出了抑制基频和二倍频共模分量和保证桥臂直流电压平衡的控制策略，最后通过仿真和实验验证了理论分析的正确性和控制策略的有效性。

1　桥臂不对称MMC-STATOCM数学模型

三相MMC-STATCOM主电路拓扑如图1所示，其直流母线无“背靠背”结构。图1中，usj、isj（j=a，b，c）分别为电网侧三相交流电压和电流，Lsj为交流侧并网电感，ipj、inj分别为上、下桥臂电流，p、n分别为正、负直流母线，直流母线电压为 Udc。MMCSTATCOM 每个桥臂由 N个相同的子单元模块（Sub-Modules，SM）和桥臂电感L串联而成。每个 SM 由两个开关器件和一个直流侧储能电容组成，构成半桥逆变单元。本文采用载波移相正弦脉冲宽度调制（Carrier Phase-Shifiting-SPWM， CPSSPWM），上、下桥臂的调制波信号互差 180°。为了维持母线电压稳定，稳态工作时满足每个时刻每相投入主电路的子模块数恒为N。

图1　三相MMC-STATCOM主电路拓扑Fig.1　Topology of a three-phase MMC-STATCOM

由于MMC-STATCOM具有三相对称的特点，本文以A相为例进行分析，其结果适用于其他各相。上、下桥臂看作可控的电压源，则单相等效电路如图2所示。

图2　单相等效电路Fig.2　Single phase equivalent circuit

由现有文献［4］分析可知，桥臂电流由共模电流和差模电流构成，即

式中，icma为 A相桥臂共模电流；idma为 A相桥臂差模电流，idma=isa。

根据基尔霍夫电压定律，对图2上、下桥臂分别列写KVL方程，即

将式（1）代入式（2）并化简得

其中

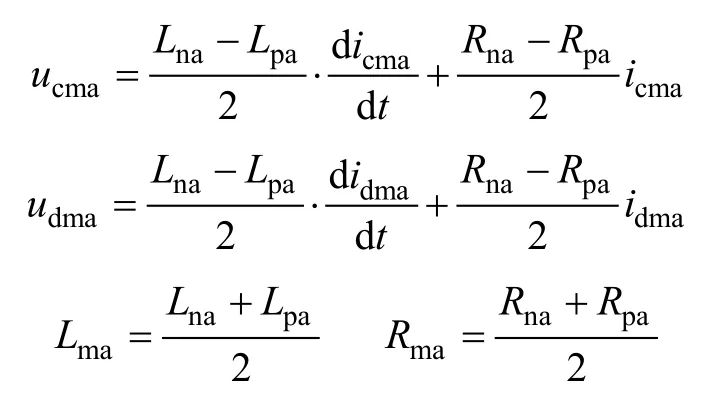
由式（3）和式（4）可得，三相MMC-STATCOM交流侧和直流侧等效模型分别如图3和图4所示。

图3　三相MMC-STATCOM交流侧等效模型Fig.3　Equivalent model of the AC side of a three-phase MMC-STATCOM

图4　三相MMC-STATCOM直流侧等效模型Fig.4　Equivalent model of the DC side of a three-phase MMC-STATCOM

从式（3）和图3可知，当上、下桥臂不对称时共模电压量ucma不为零，共模电流分量会影响到交流侧输出。同样从式（4）和图4可知，当桥臂不对称时差模电压分量不为零，差模电压分量udma也会影响到相间的共模环流分量。同时可以看出，通过控制上、下桥臂输出电压upa和una可以相应调节相输出电压（una-upa）/2以及相间共模环流icma。

在桥臂不对称时，上、下桥臂输出电压的表达式为

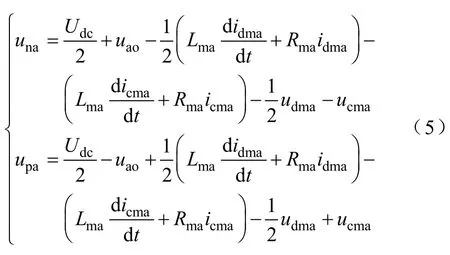
2　桥臂不对称时稳态电流分析

从上述分析可知，桥臂参数不对称会对MMCSTATCOM 的交流输出和桥臂电流产生影响。为了进一步分析桥臂参数带来的影响，将图1变换为图5所示的桥臂不对称时MMC-STATCOM等效电路。图5中和分别代表桥臂电压交流分量和直流分量。由文献［13］可知，当忽略 3次、5次等低次谐波以及与开关频率相关的高次谐波的影响，交流分量u~kj主要包含基频电压分量和二倍频电压谐波分量。此时图5所示电路可以看作线性电路，根据线性电路的叠加定理，图5可以由三个不同频率（基频、二倍频和直流）的子电路叠加构成，其等效电路分别如图6～图8所示。

图5　桥臂不对称时MMC-STATCOM等效电路Fig.5　Equivalent circuit of an asymmetrical MMC-STATCOM

图6　基于基频分量的MMC-STATCOM等效电路Fig.6　Equivalent circuit of at fundamental-frequency

由式（5）可知，上、下桥臂基频电压源幅值相等，符号相反。由于实际桥臂电阻远远小于桥臂电抗，为了简化计算，忽略桥臂电阻，根据戴维南等效电路，将上、下桥臂并联得到图6所示的基于基频分量的MMC-STATCOM等效电路，图6中u~a1、和为三相基频电压源。

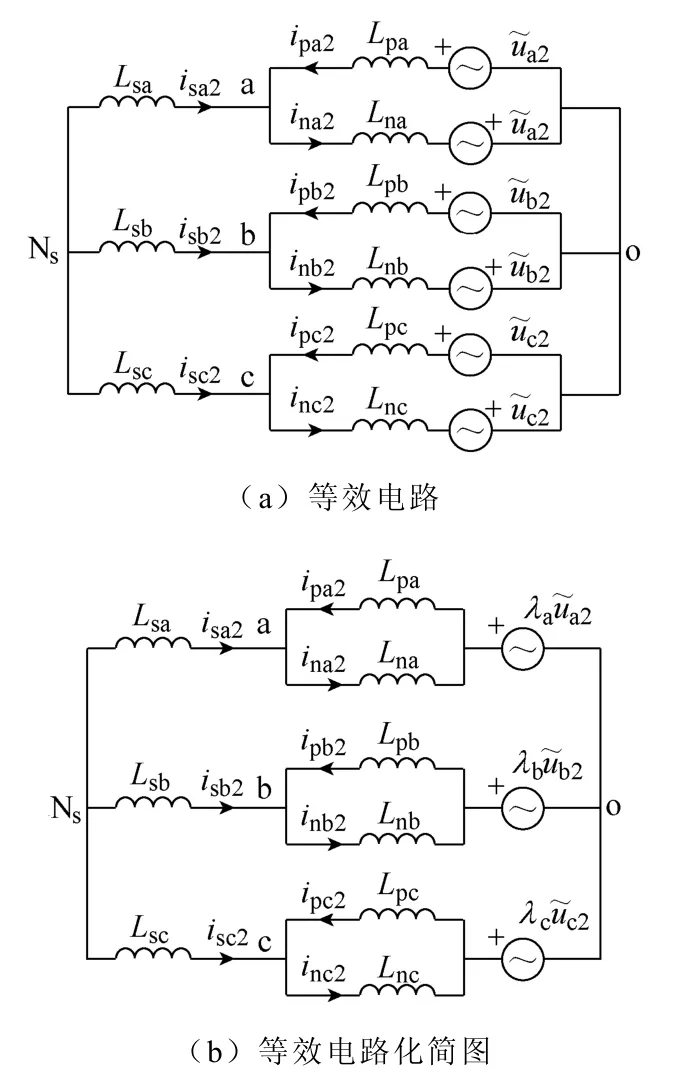
图7　基于二倍频分量的MMC-STATCOM等效电路Fig.7　Equivalent circuit of MMC-STATCOM at double-frequency

图8　基于直流分量的MMC-STATCOM等效电路Fig.8　Equivalent circuit of MMC-STATCOM based on the DC component

从图6可知，稳态时三相MMC-STATCOM上、下桥臂电流分别为

从式（6）可知，当上、下桥臂电感不相等时，交流侧基频电流在上、下桥臂之间不能平均分配，从而导致上、下桥臂电容电压波动幅值不一致以及桥臂承担无功功率容量不均衡。以A相为例，当上、下桥臂不对称时，上、下桥臂基频共模电流为

图7a为MMC-STATOCM二倍频分量等效电路，图7b为进一步化简图，图7中和为二倍频共模电压源，上、下桥臂二倍频电压源幅值相等，符号相同。

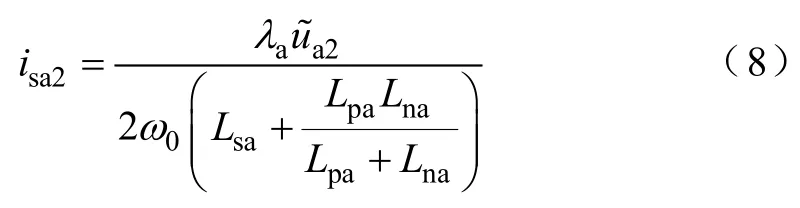
式中，ω0为基波角频率。

图8为基于直流分量的MMC-STATOCM等效电路，图 8中为直流电压源由于MMC-STATCOM直流母线无外接负载，理论上直流母线电流为零，实际上由于子模块直流侧电容放电电阻等并联型损耗的存在，每相存在共模直流电流。在对称情况下，上、下桥臂直流电流分量相等，交流侧输出直流电流为零。当MMC上、下桥臂电阻不相等时，上、下桥臂直流电流分量不相等，其差值将流入交流侧。

3　控制策略

从图6和式（6）可知，当上、下桥臂参数不对称时，交流侧电流将不能在上、下桥臂平均分配，且上、下桥臂电容电压波动幅值不同，严重时可导致开关器件因过电流或过电压而损坏，影响系统的正常运行。由图7、图8和式（7）可知，当上、下桥臂不对称时，偶次的环流分量会流入交流侧，使MMC-STATCOM 输出电流总谐波畸变（Total Harmonic Distortion， THD）增加，影响装置的性能。因此需要采用合适的控制策略，从而保证桥臂参数不对称情况下MMC-STATCOM的稳态正常运行。

从上述分析可知，通过消除基频共模电流可以保证交流侧输出电流在上、下桥臂平均分配。另外，通过抑制二倍频共模电流谐波，可以消除其对交流侧电流的影响，减小子模块直流侧电容电压脉动。通过调节直流电流，可以改善上、下桥臂直流电压的不平衡。由式（5）可知，通过调节桥臂电压分量可以相应地调节桥臂电流分量，基于此，本文分别提出了以抑制基频和二倍频共模分量控制及保证桥臂电压直流分量控制策略，其控制框图分别如图 9和图10所示。

图9　基频和二倍频共模分量控制Fig.9　Control diagram of the common-current at both fundamental and double frequency

图9中G1（s）和G2（s）为抑制基频共模电流和二倍频共模电流分量的 PR控制器分别为加入基频的二倍频共模分量控制后的上、下桥臂参考电压，其中G1（s）和G2（s）理想传递函数分别为

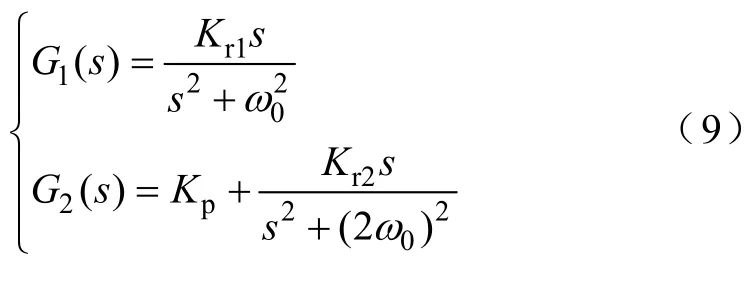
式中，Kp为比例系数；Kr1、Kr2为谐振系数。G（s）在谐振频率处具有无限大的增益，而在其他频率处大幅衰减。对于闭环系统，在谐振频率处 PR控制器输出能在相位和幅值上很好地跟踪给定值。但理想 PR控制器的带宽窄、稳定性差，当输入量频率发生波动时，PR控制器输出幅值大幅衰减，相位偏移接近±90°。为了增加系统的稳定性，可通过加入截止频率ωc适当增加PR控制器的带宽，则改进后的PR控制器传递函数为实际中的取值范围通常为5～15rad/s。

图9中，高通滤波器（High-Pass Filter， HPF）用于滤除环流中的直流分量，其截止频率可以尽可能设置的低一些（例如5Hz等）分别为A相交流共模环流分量和交流共模环流分量参考值，为了消除共模环流可设置交流共模环流分量参考值分别为基频和二倍频PR控制器的输出，通过在桥臂参考电压上叠加该分量，可以滤除相应的共模环流分量分别为上、下桥臂的基频 PR控制器输出量的比例调节系数，根据桥臂不对称度λa的大小，通过调节该比例系数可使上、下桥臂的基波电流快速达到均衡。

图10　桥臂电压直流分量控制框图Fig.10　Control diagram of the DC voltage component

图10中sign函数用来判断上、下桥臂电容的充放电状态，当电流时，上桥臂电容处于放电状态而下桥臂电容处于充电状态；反之，同理。

图11为MMC-STATCOM整体控制框图，上、下桥臂参考电压和由功率外环和电流内环而生成，通过在该桥臂参考电压上分别叠加信号和可抑制桥臂基频共模电流和二倍频共模电流，通过叠加直流信号可以消除上、下桥臂直流电压的不平衡。

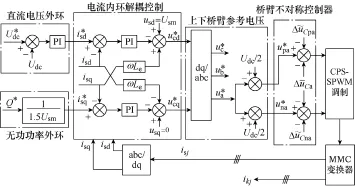
图11　MMC-STATCOM整体控制框图Fig.11　Control diagram of overall MMC-STATCOM

4　仿真和实验

为验证理论分析的正确性，在Matlab/Simulink中搭建了三相MMC-STATCOM系统，其参数见表1。

表1　MMC-STATCOM系统参数Tab.1　Parameters of the MMC-STATCOM system

4.1桥臂参数对系统稳态运行影响的仿真

为了分析桥臂不对称对MMC-STATCOM稳态运行的影响，在仿真模型中分别设置了桥臂参数一致和不一致两组情况，桥臂参数见表 2。为了便于分析，以A相为研究对象，设置桥臂参数不对称度λa为9.1%，B、C两相参数取值和A相一致。

表2　A相桥臂参数Tab.2　Parameters of A-phase bridge arm

图 12～图14分别为桥臂参数对称和不对称情况下的仿真波形对比。

图12是电流isa波形及其FFT分析，从图12中可以看出，在桥臂对称时，输出电流只含有基波分量、3次谐波分量及2n+1（n=1，2，3，6，…）次奇次谐波分量。而在桥臂参数不对称时输出电流出现了直流分量、2次谐波分量及 2n次偶次谐波分量，有效地证明了理论分析的正确性。

图12　电流isa波形及其FFT分析Fig.12　Current waveforms and FFT analysis of isa

图13　上、下桥臂电流波形Fig.13　Current waveforms of the arm current ipaand ina

图14　上、下桥臂电容电压波形Fig.14　Waveforms of the capacitor voltages in upper and lower arms

图13为上、下桥臂电流波形，表3为上、下桥臂电流谐波含量。从图13和表3可以看出，在桥臂参数不对称的情况下，上、下桥臂电流基波含量和二倍频电流含量偏差较大，导致下桥臂电流幅值大而上桥臂电流幅值较小。

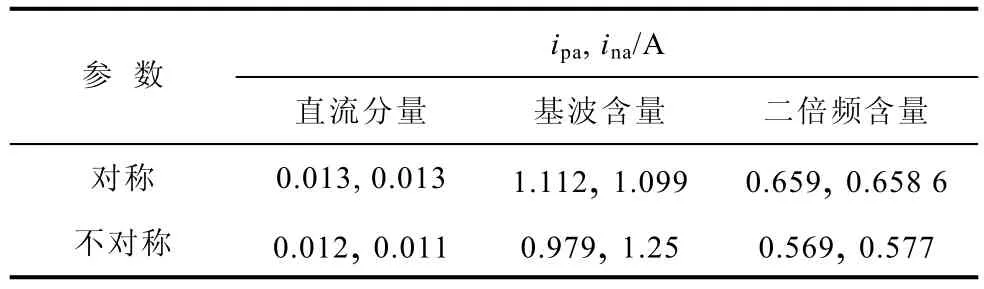
表3　上、下桥臂电流谐波含量Tab.3　The FFT analysis results of arm current

图14为上、下桥臂电容电压波形，当桥臂参数一致时，上、下桥臂电压直流分量相等，交流分量幅值相等而相位相差180°。当桥臂参数不一致时，A相上、下桥臂电容电压和直流量不再相等，可见桥臂参数的不一致，将导致上、下桥臂电压的不平衡。

4.2控制策略的仿真和实验

图 15为本文所提出的加入控制器前后的仿真波形，在t=0.3s时投入该控制策略。由图15可见，加入所述控制策略后 A相环流幅值由 1A降低至0.3A，降低了70%。同时，由于在 PR控制器中引入了上、下桥臂比例调节系数Kpa和Kna，从而能快速地解决上、下桥臂电流分配不均衡的问题，下桥臂电流峰峰值由4.5A降低至3.2A，降低了29%，使上、下桥臂电流的正弦度更高。

图15　加入控制器前后的仿真波形Fig.15　Simulation waveforms of the control strategy effect

图 16为不同输出电流下桥臂电流谐波含量曲线。从图16可见，在加入控制策略前后，桥臂电流THD明显降低，降幅最高达到了77.7%。在加入控制策略前，由于桥臂不对称上、下桥臂电流基频分量不相等，致使上、下桥臂电流THD有较大的区别，而在加入控制策略后，上、下桥臂电流基频分量基本相等，THD含量一致。

图16　不同输出电流下桥臂电流谐波含量曲线Fig.16　THD curves of bridge current under different output current

基于以上分析，在实验室搭建了一台与仿真参数一致的MMC-STATCOM实验样机，外观如图17所示，其中图17a为样机主电路实物，图17b为样机控制系统。表4为MMC-STATCOM桥臂电感。

图17　MMC-STATCOM实验样机外观Fig.17　Experimental prototype of MMC-STATCOM

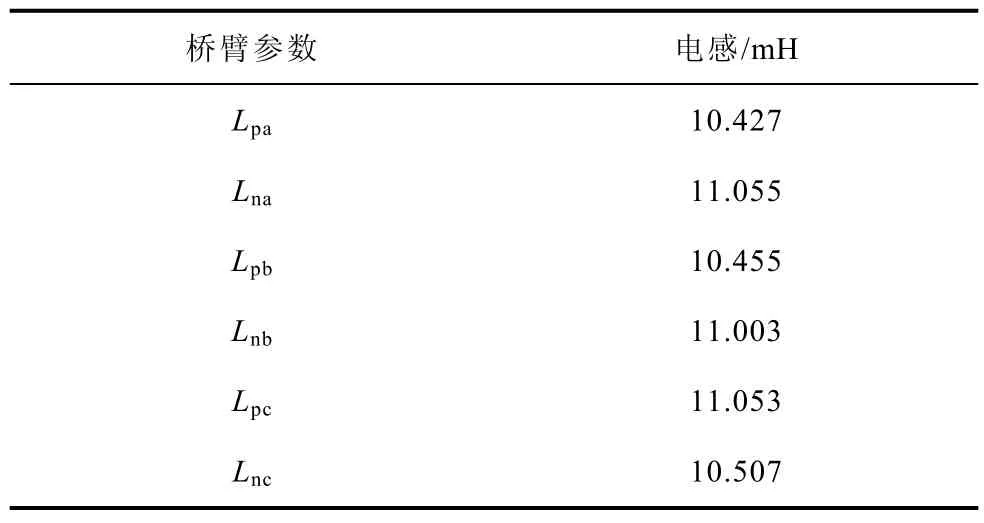
表4　MMC-STATCOM桥臂电感Tab.4　Parameters of three-phase bridge-arm inductor

图 18a～图 18c分别为加入控制策略前后的整体实验波形以及加入前后局部波形放大图。其中，通道M为A相环流分量的2倍。从图18可见，加入本文控制策略后，环流幅值在 0.4s内由 5.1A迅速减小到1.5A，降低了71%，同时上、下桥臂电流正弦度变得更高，从而减小环流带来的附加损耗。

图18　桥臂电流及环流实验波形Fig.18　Experimental waveforms of bridge arm current and circulation

图19为上、下桥臂电容电压波形，可见加入控制策略后，电容电压波动幅值由20V减小至15V，有效减小了电容电压的波动幅值，且电容电压直流分量相等。

图19　上、下桥臂电容电压波形Fig.19　Capacitor voltages waveforms of upper and lower arms

5　结论

本文对桥臂不对称MMC-STATCOM进行了研究，首先建立了桥臂不对称情况下的数学模型，然后根据等效电路详细分析了桥臂不对称对桥臂电流以及输出电流的影响，最后根据理论分析提出了相应的控制策略。

仿真和实验结果表明，桥臂参数在不对称情况下，直流和偶次环流分量会流入交流侧，且上、下桥臂电流分布不均，导致电容电压波动幅值及直流分量不一致。通过加入本文所提的基于比例谐振控制器及陷波滤波器的控制策略，有效地抑制了环流分量的大小，使上、下桥臂电流分布均匀且桥臂电流正弦度更高，降低了电容电压波动。

本文所述的控制策略其目的是实现相电流在上、下桥臂平均分配，与网侧电压、电流无关，因此在三相交流系统不对称或者三相交流瞬时功率不等情况下，本文所述的控制策略同样适用。

［1］王奎， 郑泽东， 李永东. 五电平有源中点钳位型逆变器母线中点电压平衡问题［J］. 中国电机工程学报， 2012， 32（3）： 30-36. Wang Kui， Zheng Zedong， Li Yongdong. Neutralpoint potential balancing problem of five-level active neutral-point-clamped inverter［J］. Proceedings of the CSEE， 2012， 32（3）： 30-36.

［2］刘云峰， 何英杰， 陈娟， 等. 二极管钳位多电平空间矢量与载波调制策略统一理论研究［J］. 中国电机工程学报， 2015， 35（5）： 1203-1210. Liu Yunfeng， He Yingjie， Chen Juan， et al. Research of the unity theory between space vector and carrier-based PWM modulation strategy in diode clamped multilevel inverters［J］. Proceedings of the CSEE， 2015， 35（5）： 1203-1210.

［3］刘苗， 洪峰， 尹培培， 等. 复合型级联双Buck飞跨电容五电平逆变器［J］. 电工技术学报， 2015， 30（18）：35-42. Liu Miao， Hong Feng， Yin Peipei， et al. A hybrid cascaded dual buck flying-capacitor five-level inverter［J］. Transactions of China Electrotechnical Society，2015， 30（18）： 35-42.

［4］杨晓峰. 模块化多电平变换器（MMC）研究［D］. 北京： 北京交通大学， 2011.

［5］Marquardt R， Lesnicar A. An innovative modular multilevel converter topology suitable for a wide power range［C］//IEEE Bologna Power Tech Conference， 2003， 3： 23-26.

［6］楚遵方， 李耀华， 王平， 等. 柔性直流输电系统中模块化多电平变流器的直流侧充电策略分析［J］.电工技术学报， 2015， 30（12）： 136-142. Chu Zunfang， Li Yaohua， Wang Ping， at al. Analysis of charging strategy by DC grid of modular multilevel converter in high voltage direct current transmission system［J］. Transactions of China Electrotechnical Society， 2015， 30（12）： 136-142.

［7］梁营玉， 杨奇逊， 刘建政， 等. 电网电压不平衡时MMC-HVDC的无差拍直接功率控制［J］. 电工技术学报， 2015， 30（15）： 15-25. Liang Yingyu， Yang Qixun， Liu Jianzheng， et al. Deadbeat direct power control for MMC-HVDC under unbalanced grid voltages［J］. Transactions of China Electrotechnical Society， 2015， 30（15）： 15-25.

［8］刘国伟， 姜齐荣， 魏应冬. 低频率工况下模块化多电平变流器电容电压平衡控制策略［J］. 电工技术学报， 2014， 29（8）： 166-172. Liu Guowei， Jiang Qirong， Wei Yingdong. Study on capacitor voltage balancing control of modular multilevel converters at low frequency［J］. Transactions of China Electrotechnical Society， 2014， 29（8）：166-172.

［9］曾萍. 多电平矩阵变换器在风力发电中的仿真研究［D］. 湘潭： 湘潭大学， 2011.

［10］ Pereira M， Retzmann D， Lottes J， et al. SVC PLUS：an MMC STATCOM for network and grid access applications［C］//IEEE Power Tech， Trondheim，Norway， 2011： 6.

［11］丁冠军， 丁明， 汤广福， 等. 新型多电平 VSC子模块电容参数与均压策略［J］. 中国电机工程学报，2009， 29（30）： 1-6. Ding Guanjun， Ding Ming， Tang Guangfu， et al. Sub-module capacitance parameter and voltage balancing scheme of a new multilevel VSC modular［J］. Proceedings of the CSEE， 2009， 29（30）：1-6.

［12］周月宾， 江道灼， 郭捷， 等. 模块化多电平换流器子模块电容电压波动与内部环流分析［J］. 中国电机工程学报， 2012， 32（24）： 8-14. Zhou Yuebin， Jiang Daozhuo， Guo Jie， et al. Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters［J］. Proceedings of the CSEE， 2012， 32（24）： 8-14.

［13］王鹏伍， 崔翔. MMC-HVDC三相解耦二次谐波环流抑制算法［J］. 电力系统自动化， 2013， 37（15）： 47-52. Wang Pengwu， Cui Xiang. Three phases decoupled second harmonic circulation current suppression algorithm for MMC-HVDC［J］. Automation of Electric Power Systems， 2013， 37（15）： 47-52.

［14］屠卿瑞， 徐政， 管敏渊， 等. 模块化多电平换流器环流抑制控制器设计［J］. 电力系统自动化， 2010，34（18）： 57-61. Tu Qingrui， Xu Zheng， Guan Minyuan， et al. Design of circulating current suppressing controllers for modular multilevel converter［J］. Automation of Electric Power Systems， 2010， 34（18）： 57-61.

［15］周月宾， 江道灼， 郭捷， 等. 交流系统不对称时模块化多电平换流器的控制［J］. 电网技术， 2013，37（3）： 622-628. Zhou Yuebin， Jiang Daozhuo， Guo Jie， et al. Control of modular multilevel converter under imbalance of AC power system［J］. Power System Technology，2013， 37（3）： 622-628.

［16］周月宾. 模块化多电平换流器型直流输电系统的稳态运行解析和控制技术研究［D］. 杭州： 浙江大学，2014.

［17］韩少华， 梅军， 郑建勇， 等. 模块化多电平换流器不对称桥臂的环流稳态分析［J］. 电力自动化设备，2014， 34（7）： 38-42. Han Shaohua， Mei Jun， Zheng Jianyong， et al. Steady-state analysis of unsymmetrical MMC bridgearm circulating current［J］. Electric Power Automation Equipment， 2014， 34（7）： 38-42.

［18］陈耀军， 陈柏超， 袁佳歆， 等. 模块化多电平逆变器电容电压及环流控制［J］. 电工技术学报， 2014，29（10）： 166-174. Chen Yaojun， Chen Baichao， Yuan Jiaxin， et al. The control of capacitor voltages and circulating currents of the modular multilevel inverter［J］. Transactions of China Electrotechnical Society， 2014， 29（10）：166-174.

Asymmetric Bridge Arm of Static Synchronous Compensator Based on Modular Multilevel Converter and Its Control Strategy

Qin HaihongZhao HaiweiMa CeyuDong YaowenNie Xin
（College of AutomationNanjing University of Aeronautics and Astronautics Nanjing210016China）

The modular multilevel converter （MMC） is a suitable topology for high-voltage high-capacity voltage source converter （VSC）. The MMC topology has been used in some static synchronous compensator （STATCOM） projects. Under asymmetric bridge-arm parameters， the fundamental-frequency AC currents distribute unequally between the upper and lower arms. Meanwhile，the DC and double-frequency components also flow into the AC side. In the paper， the equivalent models of the AC side and DC side of a three-phase MMC-STATCOM are established under asymmetric bridge-arm parameters. Based on the equivalent sub-circuits at different frequencies， the effects of asymmetric conditions on MMC-STATCOM operation are analyzed in detail. A novel control strategy is further proposed to suppress the common-current of fundamental-frequency and double-frequency while keeping the voltage balance between the upper and lower arms. Both simulation and experimental results validate the feasibility of the proposed method.

Modular multilevel converter， asymmetry， fundamental-frequency current， doublefrequency current， model

TM464

秦海鸿男，1977年生，博士，副教授，研究方向为功率变换技术和电机控制。

E-mail： qinhaihong@nuaa.edu.cn

赵海伟男，1990年生，硕士，研究方向为电能质量治理。

E-mail： zhaohaiwei27@163.com（通信作者）

国家自然科学基金面上项目（51277095），教育部博士点基金（20123218120017）和南京航空航天大学青年科技创新基金（理工类）（NS2015039）资助。

2015-11-27改稿日期 2016-01-31