不同刚度植物杆群对规则波传播及紊动特性影响研究

谭 超，黄本胜，刘 达，邱 静，王 珍，吉红香

(1. 广东省水利水电科学研究院 广东省水动力学应用研究重点实验室，广东 广州 510610; 2. 河口水利技术国家地方联合工程实验室，广东 广州 510610)

不同刚度植物杆群对规则波传播及紊动特性影响研究

谭 超1,2，黄本胜1,2，刘 达1,2，邱 静1,2，王 珍1,2，吉红香1,2

(1. 广东省水利水电科学研究院 广东省水动力学应用研究重点实验室，广东 广州 510610; 2. 河口水利技术国家地方联合工程实验室，广东 广州 510610)

以不同刚度硅胶圆杆群为概化植物模型，测定其抗弯弹性模量，通过波浪水槽实验，研究规则波在不同刚度植物杆群内的流速分布、紊动特征及不同刚度杆群的消浪效果。实验结果表明，当波浪通过柔性杆群时，受其摆动的影响，流速周期变化从单峰型逐渐转变成双峰型，杆群刚度越小形成的二次波峰越明显；不同刚度杆群内水体紊动强度变化显示，杆群刚度越大，造成杆群内水体的紊动强度越大；随着杆群抗弯弹性模量的增大，其消浪系数也增大，消浪系数的增长与材料的抗弯弹性模量值非线性关系，而是在某一弹性模量范围内，对消浪系数的影响较为敏感。

不同刚度植物杆群；抗弯弹性模量；流速分布；紊动强度；消浪效果

Abstract: The bending elastic modulus is measured by the conceptual plant model which is built of silica gel rod groups of different stiffness. The regular wave velocity distribution, turbulence characteristics and wave dissipation effect of different groups are studied in the laboratory experiment. Experimental result shows that when wave runs through the flexible rod groups, the velocity period changes gradually from unimodal to bimodal, and the smaller the rod stiffness is, the more obvious the secondary wave peak will be. The change of turbulence intensity in the different rod groups shows that the bigger the rod stiffness is, the bigger the turbulence intensity will be. With the increase of bending elastic modulus of rod group, the wave dissipation coefficient increases. The increase of wave dissipation coefficient is not linear with the bending elastic modulus; however, it is sensitive within a certain range of elastic modulus.

Keywords: rod groups of different stiffness; bending elastic modulus; velocity distribution; turbulence intensity; wave dissipation effect

波浪是海岸环境中最重要的动力因子，如何减少波浪对海岸的淘蚀是海岸工程研究的重要课题。植物在海岸防护中可以扮演重要角色，在海堤外滩种植物防浪林，能够使波浪到达堤前得到最大程度的消减，降低波浪的冲击力，提高大堤的安全性[1]。尽管目前人们对植物消浪的效果已有了较为充分的认识，但是对于海岸植物的消浪机理，不同波浪条件及不同植物属性(如密度、刚度、柔性、排列方式、淹没度等)下消浪效果、波浪爬高的变化，以及植物影响下波流场内动量传递、物质输运、紊流结构的特性等基础问题目前尚未有足够的研究成果及深入的理解[2]。其中基于不同刚度植物与波浪相互作用研究是海岸动力学研究的前沿问题，引起了众多国内外学者的广泛关注。在刚性植物消浪效果研究方面，Möller等[3]研究都发现波高在植物区内是指数级衰减的，最快的消减发生在植物带的前几米到十几米。Quartel等[4]对越南红河三角洲的研究发现，海岸红树林的消波能力比单纯的底摩擦高5～7.5倍。Muslesh等[5]采用刚性杆模拟刚性未淹没植物，研究植物杆径与横纵排列对水深及流速的影响。White等[6]也采用刚性杆通过试验及实地观测详细研究了植物拖曳、水流的紊动及扩散；Tschirky等[7]和 Lima等[8]的试验都表明增加植物密度可以增大波浪的消减。Mazda等[9]却发现红树林当水深超过其呼吸根高度后，水深增加波浪消减变弱，但当水深增加到红树林枝叶高度后，消减开始转而变大；在柔性植物消浪效果研究方面，Bradley等[10]定量分析了柔性海草叶片在往复流中的相对运动对波高消减的影响。Fonseca等[11]和Augustin等[12]针对海草进行的试验表明，当植物高度大于或接近水深时，消浪效果更明显，当植物处于淹没状态后，水深增加则消浪效果变弱；黄本胜等[13]设计了刚性树干和带有柔性枝叶的模型树概化物理模型，系统分析了波浪在有植物的滩地上传播变形规律以及植物的枝叶、树干和滩地宽度、滩地上水深、来波要素等对波浪传播变形的影响；蒋昌波等[14]通过波浪水槽物理模型实验，研究了孤立波在柔性植物模型前后波高、波形的变化、入射波波高、植物分布密度以及分布方式对孤立波反射、透射系数和波能衰减系数的影响。目前国内外相关研究主要集中在单一柔性或刚性植物的消浪效果的定性影响研究，对于不同刚度杆群作用下的波浪运动机理研究，特别是定量表达不同刚度杆群作用的波浪传播及紊动特性的研究较少见诸文献。

以不同刚度的硅胶圆杆群为概化植物模型，测定其抗弯弹性模量，通过波浪水槽实验，研究规则波在不同刚度植物杆群内的流速分布、紊动特征，初步探讨不同刚度杆群的消浪效果，以期加深对植物消浪机理的认识，同时也可为海岸防护工程规划设计提供科学参考。

1 实验方案设计

1.1 试验设计

本实验在波浪水槽内进行，水槽尺寸为66 m×1.0 m×1.6 m(长×宽×高)。波浪水槽首端安装有二维电机式不规则波造波系统，系统可产生周期变化范围为0.5～5.0 s、波高变化范围3～50 cm，最大水深1.2 m的各种规则波和不规则波。为消除波浪反射，在波浪槽末端设置了消波带。实验中的波高测量采用WG-50型号浪高仪，该仪器最小测量周期为1.5 s,仪器测量误差为0.4，能满足该实验的要求。不同刚度杆群内的水体三维波动流速由三维声学多普勒测速仪(Sontek 16MHz MicroADV)测量，ADV脉冲频率为16 MHz，最高采样频率为100 Hz。

在波浪水槽平坡上设置由不同刚度硅胶圆棒组成的概化植物带，在植物带前、后分别设置波高仪，定量研究波浪通过不同刚度概化植物带的衰减情况；利用ADV测量植物带内中层及底层的三维流速，以研究植物带内部水流的三维流场结构及紊动特征，中层及底层ADV测量高度分别为距底10 cm及2 cm。试验布置如图1所示。

概化植物带的圆棒直径1 cm，高度为20 cm，以横向株距5 cm、排距5 cm的方式排列成195 cm(40排)宽度(圆棒排列图见图2)，其中浅色实心圆点为圆棒位置，深色实心圆点为ADV测点位置。

波浪、水流条件设计原则为保证波浪在传播过程中不破碎、不淹没概化植物带。因此设计的滩地水深为15 cm，相应地造波板前水深为45 cm。规则波波高为5 cm、波周期为1.34 s。

图1 模型布置示意Fig. 1 Model configuration

图2 植物区圆棒排列示意Fig. 2 Rods arrangement (from left to right)

1.2 试验材料选取

选取四种不同刚度的圆柱形硅胶棒(M1～M4)，每种刚度的圆棒外形一致，圆棒直径为1.0 cm，高度为20 cm。采用悬臂梁计算公式计算了弹性模量参数，定量测定了不同材料杆群的刚度。

悬臂梁计算公式：

式中：E为弹性模量，Pa；u为偏移距离，m；F为施加的横向拉力荷载，N；I为惯性矩，对于圆形，I=πd4/64；L为圆棒长度，m。

经测量计算，得到不同材料硅胶杆弹性模量如表1所示，其中M1硅胶杆的抗弯弹性模量远大于其他材料，且在整个试验过程中的任何时刻都不会发生摆动，可视为完全刚性杆。

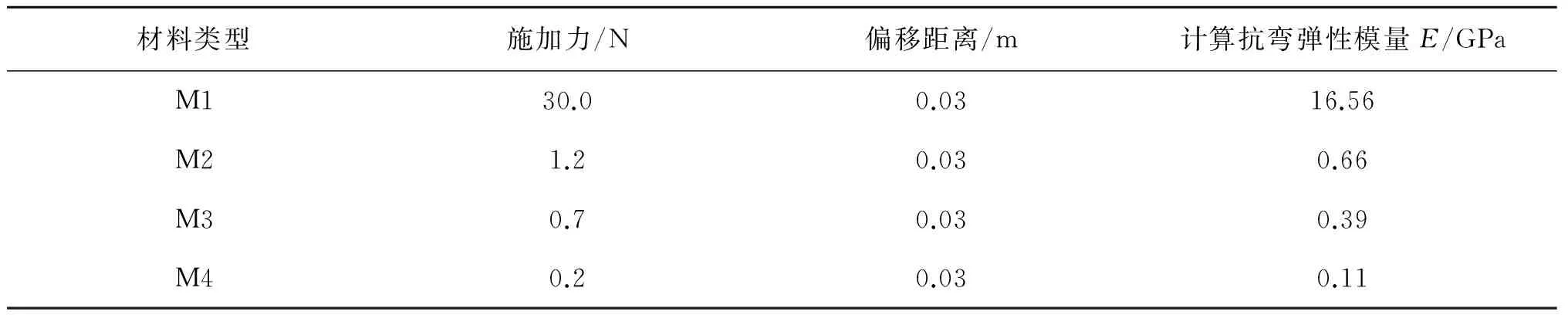
表1 不同材料硅胶杆抗弯弹性模量计算结果Tab. 1 Bending elastic modulus of different materials

2 试验结果与讨论

2.1 不同刚度杆群内的流速变化规律

2.1.1 流速峰值

波浪经过不同材料植物杆群，其流速峰值的变化尤为显著，其中杆群柔性越大，其峰值流速越小。表2统计了不同材料杆群流速峰值，试验结果表明，就同一测点而言，随着杆群柔度的增加，其中层及底层峰值流速均逐渐减小，其中，5#测点位置，M4杆群相对M1杆群，中层及底层峰值流速分别减小31%和32%。刚性杆由于不发生摆动变形，其两杆之间的波峰流速会有所增大，而柔性杆发生明显摆动，两侧杆摆动并不同步，束流作用较小，波流速的峰值反而小，这与桥墩束流流速加大的原理类似。

表2 不同刚度杆群流速峰值统计Tab. 2 The statistic of flow velocity peak value

2.1.2 相位平均流速

根据Cox等[15]闸述的原理将原始数据进行相位平均：

(2)

根据ADV测得的瞬时流速，图3给出了不同材料杆群工况下的u方向相位平均流速，图中流速曲线由50个周期的u方向瞬时流速相位平均所得，为了便于比较，将流速移至相同的相位，从图中可以看出，相位平均流速变化特征主要表现为材料柔性越大，波峰流速越小。而流速较小时，不同材料的流速值差异不明显。

图3 不同材料杆群u方向相位平均流速历时曲线(5#测点位置)Fig. 3 Phase average velocity of u direction in different rod groups (measuring point 5#)

2.1.3 波浪在柔性杆群中传播的二次波峰效应

通过试验观测及流速图发现，当波浪通过柔性杆群时(较明显的如M3杆群、M4杆群)，受柔性杆群摆动的影响，流速波峰从单峰型逐渐变成双峰型，杆群柔性越大，形成的二次波峰越明显。图4是M4杆群内的5#采样点位置的波流速过程线，从图中可以发现，无论是中层还是底层每个流速周期内都存在双峰结构。其中中层流速次峰与主峰的峰值比例为0.49∶1，底层流速次峰与主峰的峰值比例为0.31∶1，从中也可看出越靠近水面，杆摆动的幅度越大，对波速次峰的影响也越大。

图4 M4群杆内流速周期中的双峰结构示意(5#测点位置)Fig. 4 Wave velocity curve of the material 4 rod group (measuring point 5#)

2.2 不同刚度杆群内水体的紊动特征

2.2.1 紊动强度

紊动强度即为脉动流速的均方根：

图5反映了M1和M4群杆中层u方向紊动强度分布，图6表示不同材料中层和底层紊动强度分布。紊动强度沿程变化显示，杆群内紊动强度沿程表现为两个紊动高值区——进入杆群处的高值区和杆群中部的高值区，这主要是由于进入杆群处相当于两个不同介质的界面处，水流从一种介质进入另一介质而产生强烈紊动；在杆群中心区的绕流作用产生的紊动亦较为剧烈。

不同材料紊动强度变化显示，材料杆群刚度越大，杆群区流速紊动越大，其紊动强度也越大。M2～M4相对M1，杆群中部5#测点位置的u方向中层紊动强度分别减小5.1%、5.4%和4.4%。

不同方向紊动强度显示，u方向紊动强度最大，v方向次之，w方向紊动强度最小，从垂向分布看，底层的紊动强度要小于表层。这反映出经过不同刚度杆群时波浪水流具有明显的各向异性的紊流特性。

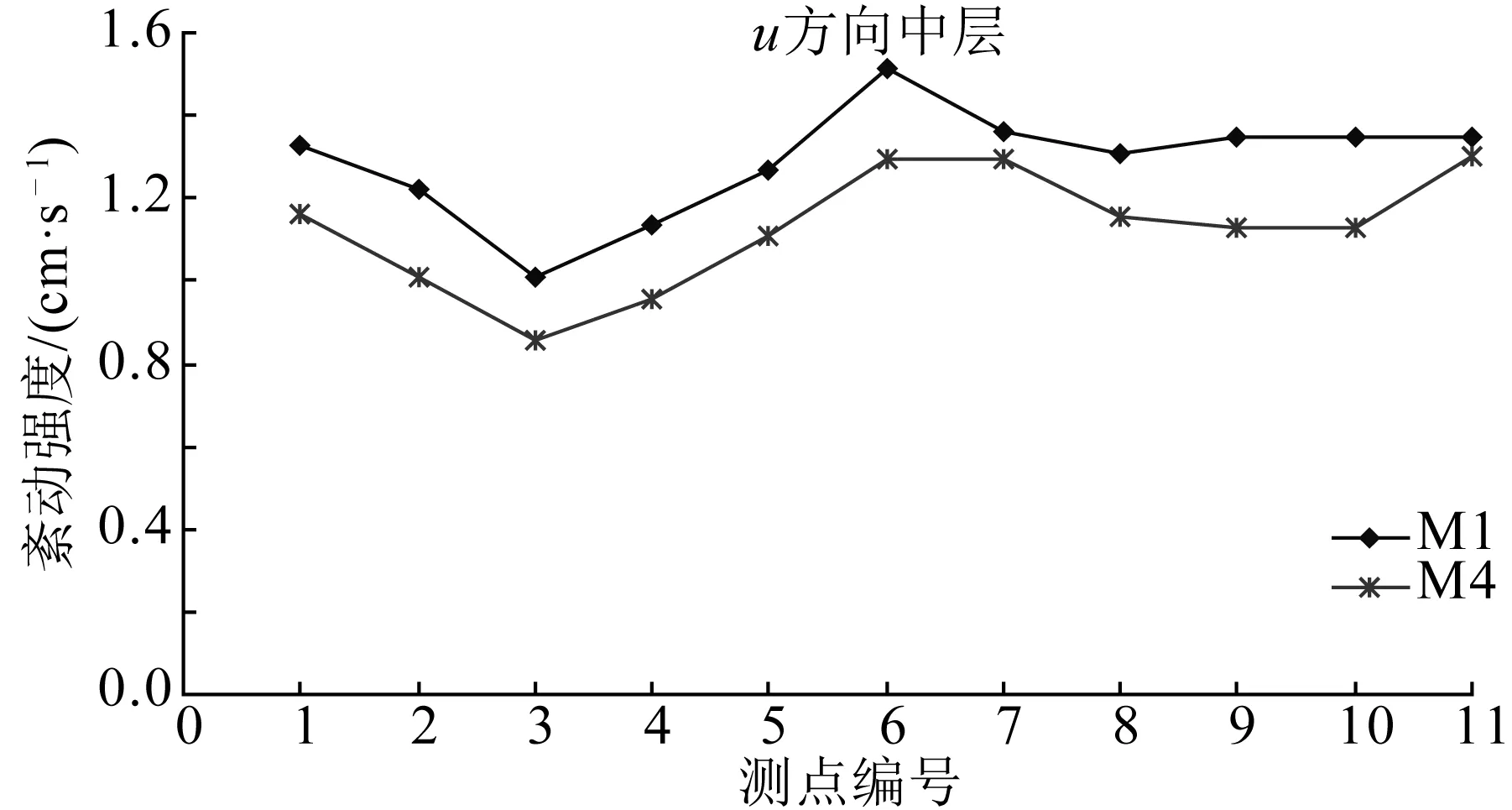
图5 不同材料u方向中层紊动强度沿程变化Fig. 5 Turbulence intensity in the u direction of material 1 and 4 rod groups

图6 不同材料中层和底层紊动强度分布(5#测点位置)Fig. 6 Middle and bottom layer turbulence distribution of different materials (measuring point 5#)

2.2.2 脉动流速概率密度

随机数据的概率密度函数，表示瞬时数据值落在指定范围内的概率。对于紊动流速过程u(t)，其值落在(u0,u0+Δu)范围内的概率定义为：

如果该随机过程满足正态分布，则其概率密度分布函数可以用式(7)表示：

图7 不同材料杆群u、v、w方向脉动流速概率密度(5#测点位置)Fig. 7 Probability density distribution of fluctuating velocity in u, v, w direction (measuring point 5#)

2.2.3 雷诺应力

雷诺应力是通过单位面积的单位流体动量交换引起的切力，其表达式为：

此外，杆群内水体中层的雷诺应力要大于底层，这与马德山[17]关于波浪紊动的研究有类似的规律，刚性杆群(M1)的中层u方向雷诺应力的值约为底层的1.14倍，较柔的杆群(M4)的中层u方向雷诺应力的值约为底层的1.52倍。

图8 不同刚度材料杆群内的雷诺应力对比(5#测点位置)Fig. 8 Reynolds stress in different rod groups (measuring point 5#)

2.2.4 能量谱密度

紊动流速过程可以看成不同频率的简谐波的叠加，即

流速过程由时域向频域的傅里叶变换称为流速过程的谱分析，紊动速度的能量谱密度[18]记为E(n)，满足

式中:T0为采样时间；E(n)为在单位频率范围内的紊动能量。能量谱密度曲线则表示时间平稳态中能量谱表示紊动动能在频带(w,w+dw)上的分布。频率的倒数是时间，能量谱中的高频成分表示快变的紊动成份，或时间尺度小的紊动[19]。

不同材料杆群内5#测点位置的u方向流速过程能量谱密度分布如图9所示。从图中可以看出，波浪在杆群中传播，均存在二个流速过程能量谱峰值，其中主峰能量值较大，次峰能量值较小，随着杆群材料刚性的降低、柔度的增加，波浪能量主峰峰值有所减小，这从另一个侧面说明了杆群材料的刚度越小、柔度越大，波浪的紊动强度就逐渐减弱这一特点。此外，值得注意的是，M4杆群次峰较M1杆群大，这与较柔性杆群的摆动引起的水流振荡有关。

图9 不同材料杆群内部5#测点位置u方向中层流速过程能量谱密度分布Fig. 9 Energy spectral density distributions in u direction of different material rod groups at measuring point 5#

2.3 不同刚度杆群的消浪效果对比

概化植物杆群前、后的波高变化可表征波能在整个概化植物带内的衰减大小。试验结果如表3所示。由表可见，杆群的抗弯弹性模量值由0.11 GPa增大到0.39 GPa，其消浪系数相应的由25.17%提高到39.79%；而当抗弯弹性模量值由0.39 GPa增大到16.56 GPa时，其消浪系数由39.79%变为40.45%，仅提高了1.66%。M2杆群与M3杆群可能恰好处于刚度不敏感区，造成消浪系数出现波动。

总体而言，随着杆群抗弯弹性模量的增大，其消浪系数是增大的，也就是说刚度越大的杆群其消能效果越明显。同时也发现，消浪系数的增长与材料的抗弯弹性模量值并不是线性关系，而是在某一弹性模量范围内，其对消浪系数的影响较为敏感，存在一个急剧变化的阶段。在该阶段内消浪系数随弹性模量增加而升高较快，但是随着弹性模量值增大到0.39 GPa以后，消浪系数增长变得极为缓慢。

对于表3的规律从试验中物理现象的观察上也可得到一定程度的解释。M3杆群和M4杆群的在波浪作用下摆动较为明显，M2杆群仅在波峰传过时做小幅摆动，而M1杆群属于完全刚性的、不摆动的，这说明M3杆群的抗弯弹性模量值与M4杆群的抗弯弹性模量值恰好在该组次的波浪水流条件下处于对摆动响应最敏感的取值范围内，也就是对消浪系数变化最敏感的范围内。

表3 不同刚度杆群前、后波高值及消浪系数统计结果Tab. 3 Wave height and wave dissipation coefficient before and after the rod groups

3 结 语

1)以不同刚度的硅胶圆杆群为概化植物模型，测定其抗弯弹性模量，通过波浪水槽实验，研究了规则波在不同刚度植物杆群内的流速分布、紊动特征及初步探讨不同刚度杆群的消浪效果。由于植物杆群的柔性作用的加强，导致植物杆起到二次造波作用，使得流速产生了明显的二次波峰，并同时削弱了主峰的强度，这表明植物的柔性效果改变了水质点的水动力学特性，形成了不同的紊流特征，并且不同的柔性(材质弹性模量)所造成的紊动特性也有所不同。

2)杆群内紊动强度的高值区存在于进入杆群处区域及杆群中部区域，这主要是由于进入杆群处相当于两个不同介质的界面处，产生强烈紊动；在杆群中心区的绕流作用产生的紊动亦较为剧烈。杆群刚度越大，造成杆群内水体流速值的紊动越大，其紊动强度值也越大；随着杆群柔性增加，其雷诺应力也随着减小，杆群中中层的雷诺应力要大于底层。

[1] 章家昌.防波林的消波性能[J].水利学报,1966,4(2):49-52.(ZHANG Jiachang. Wave dissipation effect of breakwater forest[J]. Journal of Hydraulic Engineering, 1966, 4(2):49-52.(in Chinese))

[2] 白玉川，杨建民，胡嵋，等.植物消浪护岸模型试验研究[J]. 海洋工程, 2005, 23(3): 65-69. (BAI Yuchuan, YANG Jianmin, HU Mei, et al. Model test of vegetation on the bank to attenuate waves and protect embankments[J].The Ocean Engieering, 2005, 23(3):65-69. (in Chinese))

[3] MOLLER I, SPENCER T. Wave dissipation over macro-tidal saltmarshes: Effects of marsh edge typology and vegetation change[J]. Journal of Coastal Research, 2002, S136: 506-521.

[4] QUARTEL S, KROON A, AUGUSTINUS P G E F, et al. Wave attenuation in coastal mangroves in the Red River Delta, Vietnam[J]. Journal of Asian Earth Sciences, 2007, 29(4): 576-584.

[5] MUSLESH F A, CRUISE J F. Functional relationshipsof resistance in wide flood plains with rigid unsubmergedvegetation[J]. Journal of Hydraulic Engineering, 2006, 132(2): 163-171.

[6] WHITE B L, NEPF H M. A vortex-based model ofvelocity and shear stress in a partially vegetated shallowchannel [J]. Water Resources Research, 2008, 44(1): W01412.

[7] TSCHIRKY P, HALL K, TURCKE D. Wave attenuation by emergent wetland vegetation[C]//Proceedings of the 27th International Conference on Coastal Engineering, ASCE. 2000: 865-877.

[8] LIMA S F, NEVES C F, ROSAURO N M L. Dampingof gravity waves by fields of flexible vegetation[C]//Proceeding of the 30thInt. Coast. Eng. Conf. 2006: 491-503.

[9] MAZDA Y, MAGI M, LKEDA Y, et al. Wave reduction in a mangrove forest dominated by Sonneratia sp[J]. Wetlands Ecology and Management, 2006, 14(4): 365-378.

[10] BRADLEY K, HOUSER C. Relative velocity of seagrass blades: Implications for wave attenuation in low energy environments[J]. Journal of Geophysical Research, 2009, 114: F01004.

[11] FONSECA M S, CAHALAN J A. A preliminary evaluation of wave attenuation by four species of seagrass[J].Estuarine, Coastal, and Shelf Science, 1992, 35(6): 565-576.

[12] AUGUSITIN L N, IRISH J L, LYNETT P. Laboratory and numerical studies of wave damping by emergent and near emergent wetland vegetation[J]. Coastal Eng., 2009, 56(3):332-340.

[13] HUANG Bensheng, LAI Guanwen, QIU Jing,et al. Hydraulice of compound channel with vegetated flood plains[J]. Journal of Hydrodynamics, Ser.B, 2002: 23-28.

[14] 蒋昌波，王瑞雪，陈杰，等.非淹没刚性植物对孤立波传播变形影响试验[J].长沙理工大学学报：自然科学版,2012,9(2):50-55. (JIANG Changbo, WANG Ruixue, CHEN Jie, et al. Laboratory investigation on solitary wave transformation through the emergent rigid vegetation[J]. Journal of Changsha University of Science and Technology,2012,9(2):50-56. (in Chinese))

[15] COX D T, KOBAYASHI N, OKAYASU A. Experimental and numerical modeling of surf zone hydrodynamics[R]. Delaware: Univercity of Delware, 1995:32-50.

[16] 杨克君,刘兴年,曹叔尤,等.植被作用下的复式河槽漫滩水流紊动特性[J]. 水利学报,2005,36(10)：1263-1267.(YANG Kejun, LIU Xingnian, CAO Shuyou, et al. Turbulence characteristics of overbank flow in compound river channel with vegetated floodplain[J]. Journal of Hydraulic Engineering, 2005, 36(10)：1263-1267. (in Chinese))

[17] 马德山.波浪紊动及紊动要素的计算[J].天津大学学报,1964,4(14)：16-19.(MA Deshan. Wave turbulence and calculation[J]. Journal of Tianjin University,1964,4(14)：16-19.(in Chinese))

[18] 槐文信,韩杰,曾玉红,等.淹没柔性植被明渠恒定水流水利特性的试验研究[J].水利学报,2009,40(7)：791-798.(HUAI Wenxin, HAN Jie, ZENG Yuhong, et al. Experimental study on hydraulic behaviors of steady uniform flow in open channel with submerged flexible vegetation[J]. Journal of Hydraulic Engineering, 2009,40(7)：791-798. (in Chinese))

[19] 崔成 张宁川，郭川胜,等.变水深对畸形波及其时频能量谱的影响[J]. 海洋学报,2011,33(6)：174-179.(CUI Cheng, ZHANG Ningchuan, GUO Chuansheng, et al. Impact of water depth variation on simulated freak waves and their time-frequency energy spectrum[J]. Acta Oceanologica Sinica,2011,33(6)：174-179. (in Chinese))

Preliminary study on effect of rod groups of different stiffness on regular wave propagation and turbulence characteristics

TAN Chao1, 2, HUANG Bensheng1, 2, LIU Da1, 2, QIU Jing1, 2,WANG Zhen1, 2, JI Hongxiang1, 2

(1. Guangdong Research Institute of Water Resources and Hydropower, Guangdong Provincial Key Laboratory of Hydrodynamics, Guangzhou 510630, China; 2. National Engineering Laboratory of Estuary Hydropower Technology, Guangzhou 510630, China)

TV139.2

A

10.16483/j.issn.1005-9865.2016.06.005

1005-9865(2016)06-0038-08

2016-01-17

国家自然科学基金(41476073)；广东省水利科技创新基金(2011-08，2012-03，2015-48)

谭 超(1985-)，男，湖南长沙人，高级工程师，博士生，主要从事河口海岸动力学研究。E-mail: gdsky_tanchao@foxmail.com