一维全非线性Green-Naghdi水波方程数值模型

焦子峰，尹 晶,2，房克照，孙家文,2

(1. 大连理工大学 海岸和近海工程国家重点实验室 DUT-UWA海洋工程联合研究中心，辽宁 大连 116024; 2. 国家海洋环境监测中心，辽宁 大连 116023)

一维全非线性Green-Naghdi水波方程数值模型

焦子峰1，尹 晶1,2，房克照1，孙家文1,2

(1. 大连理工大学 海岸和近海工程国家重点实验室 DUT-UWA海洋工程联合研究中心，辽宁 大连 116024; 2. 国家海洋环境监测中心，辽宁 大连 116023)

建立了求解一维全非线性Green-Naghdi水波方程的中心有限体积/有限差分混合数值格式。采用结构化网格对守恒形式的控制方程进行离散和积分，界面数值通量采用有限体积法计算，剩余项则采用中心有限差分格式求解。其中，采用中心迎风有限体积格式计算控制体界面数值通量，并结合界面变量的线性重构方法，使其在空间上具有四阶精度，通过引入静压重构技术和波浪破碎指标使模型具备处理海岸水-陆动边界及波浪破碎的能力。时间积分则采用具有总时间变差减小(Total Variation Diminishing, TVD)性质的三阶龙格-库塔法进行。应用该模型对孤立波在常水深和斜坡海岸上的传播过程及规则波跨越潜堤传播的实验进行了数值模型研究，数值计算同解析解及实验数据吻合良好。

Green-Naghdi水波方程；混合格式；中心迎风格式；水-陆动边界；波浪破碎

Abstract: A 1D Green-Naghdi model based on hybrid central finite-volume/finite-difference method is presented in this paper. The convective flux in the conservative governing equations is estimated using finite-volume method while the remaining terms are discretized using finite-difference method. Central upwind finite-volume scheme, in conjunction with fourth-order MUSCL method for variables reconstruction, is used to compute the interface flux. By introducing the hydrostatic reconstruction technique and wave breaking index, the model has the ability to deal with the coastal moving shoreline and wave breaking. The third-order Runge-Kutta method with TVD property is adopted to perform time marching. The propagation of solitary wave on plane and sloping beach and the experiment of regular propagating over a submerged sill are computed with this model. The numerical results are in good agreement with analytical and experimental data.

Keywords: Green-Naghdi wave equations; hybrid scheme; central upwind scheme; moving shoreline; wave breaking

准确模拟波浪地传播变形对海岸工程和海洋工程研究具有重要的意义。尽管直接求解水波欧拉方程的数值方法在近几年有较快地发展[1]，Boussinesq模型仍然是研究工程尺度范围内波浪传播变形问题最为广泛的手段之一(如开源模型FUNWAVE[2]和COULWAVE[3]及丹麦DHI公司开发的MIKE21商业软件波浪模块等)。早期的Boussinesq方程通常仅具有弱非线性特征，只适用于小波幅波浪地模拟，经过几十年的研究，目前Boussinesq类水波方程的相关理论已达到了一个较高的水平，为强非线性波浪的数值计算奠定了基础[4-5]。Green-Naghdi水波方程[6]是较为经典的、具有全非线性特征的Boussinesq类水波方程，可用于研究非线性强和水深相对较深条件下波浪传播问题(仅具有弱色散性)，因此，近几年基于Green-Naghdi水波方程展开的数值计算层出不穷[7-8]。由于Boussinesq类方程通常含有高阶导数项(包括色散项和非线性项)，不便于采用诸如有限元和有限体积方法求解，一般采用有限差分方法进行求解[9]。虽然有限差分方法简单明了、易于编程，但采用有限差分方法的数学模型易产生高频数值震荡，当非线性较强或者海床地形变化较大时尤为突出，经常导致计算失败，即便采用光滑器稳定计算仍然不能从根本上解决上述问题[10]。且Boussinesq类模型在处理海岸水-陆动边界和波浪破碎时通常采用近似方法，引入过多可调参数，这不但给实际应用带来不便，某种程度上也加剧了模型的不稳定。完全非线性浅水方程和Boussinesq水波方程同属浅水方程范畴，忽略高阶非线性和色散项后，Boussinesq水波方程可退化为完全非线性浅水方程。完全非线性浅水方程属于典型双曲守恒律方程，这类方程有许多基于高分辨率有限体积格式的高精度解法[10]，且多以黎曼间断解问题为理论基础。而海岸水-陆动边界问题本质上属于黎曼问题，正适合采用完全非线性浅水方程进行描述。此外，由于波浪破碎时Boussinesq方程中高阶非线性项和色散项可以忽略不计[10]，破碎波仍可利用完全非线性浅水方程能够捕捉间断这一特点进行计算，因此采用高分辨率有限体积格式求解Boussinesq类水波方程具有重要的意义。鉴于Boussinesq类水波方程的表达式较为复杂，目前以发展有限体积/有限差分混合格式为主，这类数值格式具备稳定性强、处理波浪破碎和海岸水-陆动边界简单的特点[11-13]。

有限体积法的数值实现重点体现在网格界面处数值通量的计算，通常采用迎风格式和中心格式。高阶迎风格式精度高，但需要精确或者近似求解黎曼问题，构造过程相对繁琐，计算量大，对于实际应用而言，较准地求解黎曼解不是一件易事[10]；中心格式构造简单，但容易出现数值震荡。近几年出现的中心迎风格式兼具迎风格式精确性和中心格式简单性优点。中心迎风格式无需求解复杂的黎曼问题，程序实现简单，目前采用中心迎风格式求解Green-Naghdi水波方程中数值通量的研究并未见诸刊物，其精度和稳定性等尚需进一步考察。

文中将中心迎风有限体积格式应用于Green-Naghdi水波方程数值通量的求解，同时为了处理近岸波浪计算常遇到的水-陆动边界现象，采用静压重构技术保证计算的稳定性和水深h的非负性。该混合格式充分利用有限体积方法弥补有限差分方法在数值计算稳定性和处理波浪破碎及水-陆动边界问题的不足。通过模拟孤立波在常水深和斜坡海岸上的传播及规则波跨越潜堤传播实验对所建模型验证，数值计算结果与解析解和实验数据及其他模型计算所得结果进行对比，结果表明，中心迎风格式在程序编制难易程度、计算精度和计算效率等方面具有一定的优势。

1 数学模型

1.1 控制方程

一维全非线性弱色散性Green-Naghdi方程表达式[6,15]：

其中，d=η+h为总水深，η为波面，h为静水水深，u为水深平均速度，zb为水底高程，g为重力加速度。下标t和x分别表示变量对时间t和空间x的偏导数。式中，Φ和Ψ分别为：

对于平底海床，水底高程zb为常数，即zb对空间变量x的导数为0，因此方程(1)可以改写为：

本文所建的一维Green-Naghdi水波方程模型将采用方程(1)作为控制方程。当Φ=Ψ=0时，方程(1)和(3)分别与非平底海床和平底海床的浅水方程相一致。

为便于使用有限体积格式，将上述控制方程改写为守恒形式：

其中，U为变量矢量，F为通量矢量，定义为：

式中：

为利用具有和谐性质的高精度有限体积格式处理海岸水-陆动边界问题引入水位ζ(=zb+d)。式(4)中S为源项，方便起见，将其分成三个组成部分，分别为水底坡度项Sh、水底摩擦项Sf和色散项Sd，即：

其中，水底摩擦项由常用的二次律公式给出τ=-fu|u|，其中，f为水底摩擦系数，通常取值范围是0.000 1～0.01。式(7)中的色散项由下式给出：

1.2 方程空间离散与时间积分

将式(4)在整个控制体单元格上积分，得到下式：

式中：Ω为单元区域；Γ为单元边界；nx为外法向量。

采用矩形网格单元，将计算域在空间、时间上均匀划分单元网格，做如下离散xi=iΔx(i=1,…,I)，tn=nΔt(n=1,…,N)，其中Δx，Δt分别为空间、时间步长。波面η和速度u均定义在控制体中心。在有限体积[xi-1/2,xi+1/2]×[tn,tn+1]内应用方程(9)，采用对时间的差分近似为对时间的微分，并用差分代替导数，可得：

式中，Uin为n时刻解U在单元Ii∈[xi-1/2,xi+1/2]内的空间平均值，Fi+1/2为单元边界xi+1/2处的数值通量，Fi-1/2为单元边界xi-1/2处的数值通量，Si为单元Ii对应的数值源项。

基于Kurganov和Petrova提出的中心迎风格式[16]，式(10)中的单元界面数值通量可以通过下式计算：

显然，中心迎风格式的有限体积法构造相对简洁并且不需要求解复杂的黎曼问题，因此中心迎风格式的程序编制更为简单，二维情况下，这一优势将更加明显。

上述中心迎风格式仅为一阶精度，为了提高空间精度，采用四阶高精度状态差值方法(MUSCL)[17]对界面左右变量进行重构，重构后的界面变量再按照上述步骤进行。模型的时间积分采用具有TVD性质的三阶龙格-库塔方法[10]：

为保证计算收敛，时间计算步长由Courant-Friedrichs-Lewy(CFL)稳定性限制条件确定：

其中，ν为常数，对于本文计算，取ν=0.2。

1.3 边界条件与波浪破碎的处理

模型中涉及的边界条件包括固壁边界、造波边界和水-陆动边界。固壁边界条件通过在计算域两端分别设置3个虚拟网格实现，虚拟网格的变量通过固壁处法向速度为零，切向速度导数为零赋值。计算中涉及孤立波和规则波的生成，前者通过在计算域内给定初始波面和流速作为入射波浪，后者采用在连续方程中增加源项的方法生成所需波浪，且根据需要在计算域两端设置海绵层避免波浪二次反射的问题[14]。水-陆动边界条件是波浪计算的难点，本文也是充分利用有限体积法求解完全非线性浅水方程的优势，将水-陆动边界处理为间断。具体方法是通过在状态重构过程中(MUSCL)采用静压重构技术实施[18]，该技术的特点就是将水-陆动边界附近的海床视为随时间做微小变动的，通过在计算过程中对海床的调整达到较准确地捕捉水-陆动边界的目的。与常用的薄层水体法相比，该方法具有更高的精度，且保证了重构水深非负和水-陆动边界处的和谐性，这对计算的稳定性和精度非常重要。具体执行步骤如下：

第一步：利用已知变量(p,ζ,d)采用MUSCL方法重构网格界面左右状态变量：

在此过程中，引入一极小水深作为判断网格干、湿状态的阙值(d<10-4m)，如某网格水深小于此值认定为干网格，界面流速直接赋值为零。同理，可得到界面右侧的速度值。需要注意的是，当某一个网格的相邻网格有干网格出现时，该网格以及干网格内的变量分布认为常数。

第二步：确定界面处水底高程值并进行非负水深重构，如下：

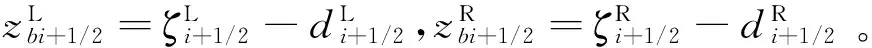
同理将上述过程用于右侧界面，可得到右侧界面状态变量取值。

第三步：对水-陆边界附近的网格进行调整，即定义：

然后对zb进行修正如下：

将通过式(16)-(20)进行的变量重构过程用于数值通量的计算。为了获得和谐解，对于方程中的底坡源项要做如下相应处理[10]：

处理波浪破碎问题时采用文献[10]给出的方法，即当波高与水深之比达到0.8时，认为波浪发生破碎，Green-Naghdi水波方程退化为完全非线性浅水方程，将破碎波浪处理为间断。

2 数值验证

针对上文所建立的混合格式模型，本节将通过几个典型算例的数值模拟分别对其进行验证。其中，算例一为常水深孤立波的长距离传播问题，用于验证模型的精度；算例二为破碎和非破碎孤立波在斜坡海岸上的传播问题，用于检验模型捕捉水-陆动边界和模拟破碎波浪的能力；算例三为规则波跨越潜堤传播，用于检验模型对强非线性波浪模拟的能力。需要指出，所有计算均未使用人工光滑器。

2.1 孤立波在常水深水槽中的传播

孤立波是波浪色散性和非线性平衡制约的典型代表，其在常水深水槽中长距离传播的数值模拟是检验数值模型的有力工具。而且，对于一维Green-Naghdi水波方程，孤立波存在精确解[19]，可以用来验证模型数值格式的精确性。

在本算例中，计算域长度450 m，静水水深h0为1.0 m，在计算域内给出孤立波解析解作为初始条件，波高H=0.6 m，孤立波从计算域的左侧向右侧传播，初始时刻波峰位于x0=50 m处，网格尺寸Δx=0.10 m，忽略底摩擦的影响，且计算域两端采用固壁边界条件。图1(a)给出了采用中心迎风格式模拟的孤立波在t=0 s, 20 s, 40 s, 60 s和80 s时的波面状态。从图中可见，经过长距离的传播，孤立波的波形和波高值均保持稳定，几乎未发生变化，表明所建立的数值格式没有引入伪色散和数值耗散。图1(b)为在时间t=80 s时，模型计算结果与解析解的比较，可以看出两者高度吻合，说明本模型具有较好的精确性。

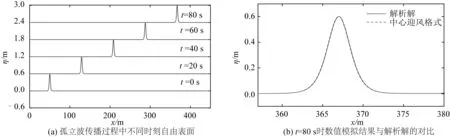
图1 孤立波的长距离传播Fig. 1 The propagation of a solitary wave over a long distance

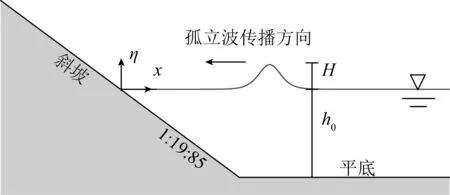
图2 孤立波爬坡实验海床Fig. 2 The sketch of experimental setup of solitary wave runup

2.2 孤立波在斜坡海岸上的爬坡

本节将用所建立的Green-Naghdi模型模拟孤立波在斜坡上的爬高实验[20]，这些实验结果被广泛的用于检验波浪爬高模型，实验海床如图2所示，是一个坡度为1∶19.85的斜坡海岸。

首先进行非破碎孤立波的爬坡模拟，孤立波的波高与水深之比H/h0=0.018 5，静水水深h0=0.39 m。计算域的长度为90 m，网格长度Δx= 0.05 m，底摩擦系数取cf= 0.001。对计算结果进行以下无因次处理：

图3中绘出了H/h0=0.018 5时，无量纲时间t*= 30, 40, 50, 60, 70时波形空间分布图，x*=0对应初始岸线。将数值计算结果与实验结果进行对比，如图3(a)和图3(b)所示，数值计算结果稍超前于实验结果，图3(c)和图3(d)较好地复演了孤立波爬坡及回落过程，而图3(e)中水面与斜坡交界处较明显的差别，这可能是因为黏性影响的结果[7]。对于该组物理模型实验，Li等[7]采用基于有限元方法的Green-Naghdi方程模型进行过数值模拟，计算结果也一并在图3中给出，可见其与本文计算结果基本一致。该算例说明模型能够有效地模拟非破碎孤立波在海岸上的传播、爬坡和回落过程中波浪的运动状态。

其次模拟破碎波孤立波在斜坡海床上的爬高。设置孤立波波高与水深之比H/h0=0.3，其他条件不变。如图4，取无量纲时间t*= 15, 20, 25, 30时数值模拟结果与实验结果以及Li等[7]的数值计算结果进行对比，波面同样采用无量纲形式。从图4(b)中可以看到，数值计算结果由于孤立波的提前破碎，造成波面的计算结果小于实验结果，且波前近乎垂直，但这并未影响波浪爬坡和回落的演化过程。数值计算结果与实验结果吻合程度高，而偏小于Li等的数值计算结果，但各时刻的运动特征模拟均吻合较好。这说明本文所建立的Green-Naghdi模型能充分描述破碎孤立波传播、爬坡及回落过程中典型的运动特征，有效验证了模型的精度，同时说明了本模型具有较好的处理水-陆动边界及波浪破碎的能力。

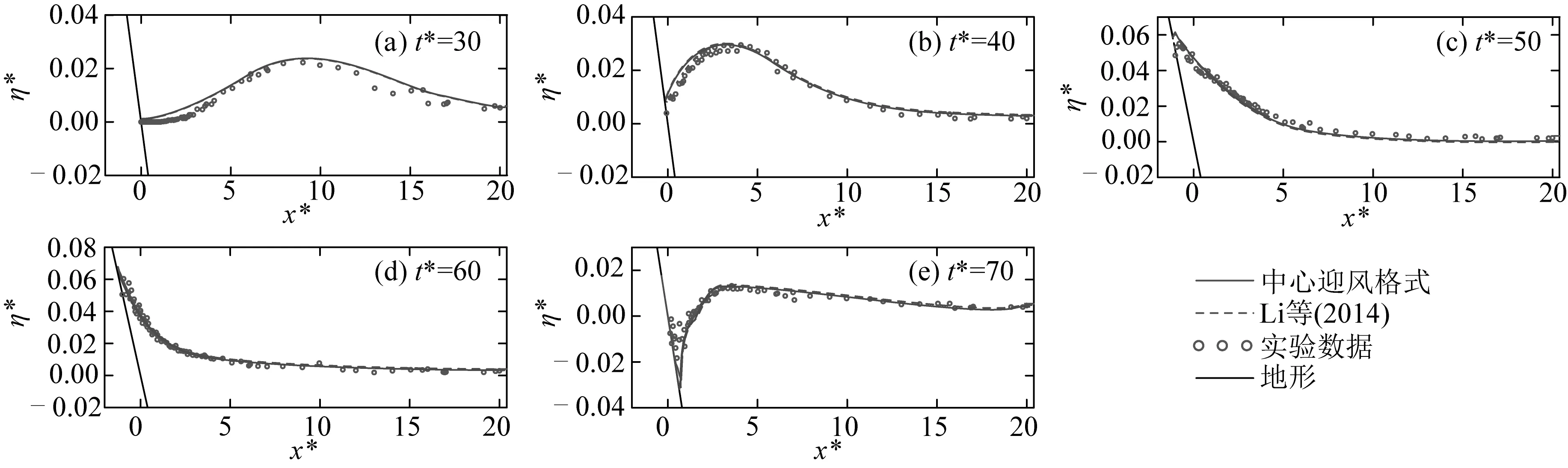
图3 H/h0=0.018 5时孤立波波面数值计算结果和实验数据对比Fig. 3 Comparison of simulated and experimental surfaces of a solitary wave with H/h0=0.018 5

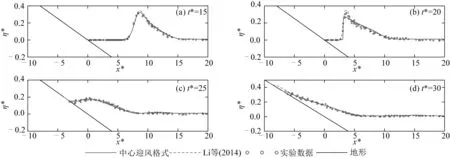
图4 H/h0=0.3时孤立波波面数值计算结果和实验数据对比Fig. 4 Comparison of simulated and experimental surfaces of a solitary wave with H/h0=0.3

2.3 规则波在潜堤海床上的传播

规则波跨越潜堤传播是非常复杂的波浪演化过程，涉及波浪的变浅、高次谐波产生释放等，是检验模型色散性和非线性综合性能的有力工具。采用Dingemans[21]的规则波跨越潜堤传播的实验来对数值模型检验，实验海床设置在图5中给出，海床两端设置1.5倍波长海绵层吸收波浪，造波机在x=0 m处，平底处静水水深为0.4 m，梯形坝的坡脚位于x=6.0 m处，梯形坝顶端长为2.0 m，距离静水面0.1 m，梯形潜堤前坡坡度为1∶20，后坡坡度为1∶10，根据Dingemans[21]的实验，在计算域内设置10个浪高仪，位置分别为x=2 m, 4 m, 10.5 m, 12.5 m, 13.5 m, 14.5 m, 15.7 m, 17.3 m, 19 m和21 m。入射波波高H=0.02 m，周期T=2.02 s，计算网格长度为Δx=0.025 m。

图5 规则波跨越潜堤传播实验布置示意Fig. 5 The sketch of experimental setup of regular waves propagation over submerged bar

图6给出了10个浪高仪位置上数值模拟结果与实验数据的对比。如图6所示，规则波跨越堤顶传播过程中，波浪受到潜堤的影响，波形发生明显变化，潜堤前以及堤顶位置处波面的数值计算结果与实验数据吻合程度高，说明模型能够准确模拟规则波的传播及跨越潜堤时的波浪状态。但是，在堤后浪高仪(例如x≥15.7 m)波面时间序列图中可以看到，数值计算结果与实验结果在波幅和相位上均有较明显地差别，这是因为规则波跨越潜堤后的波浪中包含了具有强色散性的高频自由波，而本文所使用的Green-Naghdi方程仅具有弱色散性，对强色散性波浪的模拟效果较差。使用高级别Green-Naghdi方程，例如GN-5方程，可得到更为精确的数值结果[22](本文采用方程为GN-1型方程)。

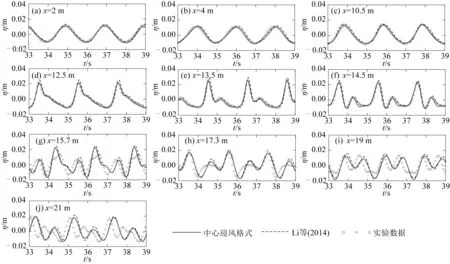
图6 规则波跨越潜堤传播各浪高仪处的波面时间序列Fig. 6 Time series of surface elevations for regular waves passing over a submerged bar

图6中同时给出Li等[7]的对该物理模型实验的数值计算结果，可见其与本文计算结果基本一致，但存在一些细节差别。在图6(a)-(f)测点处，本文模型计算结果与Li等的计算结果吻合程度较高，而在图6(g)-(j)测点处Li等波面幅值计算结果均偏高于本模型计算结果，尽管如此，两者差异较小，而且相位吻合程度高，这进一步证明了数值模型的精度与正确性。

3 结 语

将中心迎风格式应用于建立求解一维全非线性Green-Naghdi水波方程的混合数值格式。对守恒形式控制方程中的通量项，采用有限体积方法离散和积分，应用中心迎风格式求解界面处数值通量，界面左右变量则通过四阶状态插值方法重构，同时结合静压重构技术保证计算域内的和谐性和重构水深非负性。方程中剩余项采用有限差分方法进行求解。应用具有TVD性质的三阶龙格-库塔方法进行时间积分。针对典型算例进行了数值模拟，结果表明所建立的数值模式具有稳定性强、间断捕捉、处理海岸水-陆动边界及波浪破碎方便等优点。应用典型算例对所建模型进行了验证，数值计算结果与解析解、实验数据及其他模型计算结果吻合良好，综合考虑程序编制难易程度、计算精度和计算效率等方面，中心迎风格式值得在Green-Naghdi水波方程的求解方面进行推广和应用。

[1] CHOI D Y, WU C H, YOUNG C C. An efficient curvilinear non-hydrostatic model for simulating surface water waves [J]. International Journal for Numerical Methods in Fluids, 2011, 66(9): 1093-1115.

[2] KIRBY J T, WEI G, CHEN Q, et al. FUNWAVE 1.0: fully nonlinear Boussinesq wave model-Documentation and user's manual [R]. University of Delaware, 1998.

[3] LYNETT P J． Nearshore wave modeling with high-order Boussinesq-type equations [J]． Journal of Waterway, Port, Coastal and Ocean Engineering, 2006, 132(1): 348-357．

[4] 李孟国, 王正林, 蒋德才. 近岸波浪传播变形数学模型的研究与进展 [J]. 海洋工程, 2002, 20(4): 43-57. (LI Mengguo, WANG Zhenglin, JIANG Decai. A review on the mathematical models of wave transformation in the nearshore region [J]. The Ocean Engineering, 2002, 20(4): 43-57. (in Chinese))

[5] 周俊陶, 林建国, 谢志华. 高阶Boussinesq类方程数值求解及试验验证 [J]. 海洋工程, 2007, 25(1): 88-92. (ZHOU Juntao, LIN Jianguo, XIE Zhihua. Numerical simulation for higher-order Boussinesq type equations and experimental verifications [J]. The Ocean Engineering, 2007, 25(1): 88-92. (in Chinese))

[6] GREEN A E, NAGHDI P M. A derivation of equations for wave propagation in water of variable depth [J]. Journal of Fluid Mechanics, 1976, 78(02): 237-246.

[7] LI M, GUYENNE P, LI F, et al. High order well-balanced CDG-FE methods for shallow water waves by a Green-Naghdi model [J]. Journal of Computational Physics, 2014, 257: 169-192.

[8] 赵彬彬, 段文洋. 全非线性深水波的Green-Naghdi理论研究 [J]. 哈尔滨工程大学学报, 2009,8: 860-866. (ZHAO Binbin, DUAN Wenyang. Research on the Green-Naghdi theory for fully nonlinear deep water wave [J]. Journal of Harbin Engineering University, 2009,8: 860-866. (in Chinese))

[9] 朱良生, 洪广文. 任意水深变化Boussinesq型方程非线性波数值计算 [J]. 海洋工程, 2000,18(2): 29-37. (ZHU Liangsheng, HONG Guangwen. Numerical calculation of no nlinear wave using Boussinesq equation in water of arbitrarily varying depths [J]. The Ocean Engineering, 2000,18(2): 29-37. (in Chinese))

[10] SHI F, KIRBY J T, HARRIS J C, et al. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation [J]. Ocean Modelling, 2012(2): 36-51.

[11] 岳良毅, 汪学锋, 尤云祥. 扩展型Boussinesq水波方程的一种改进有限体积/有限差分混合算法[J]. 水动力学研究与进展：A辑, 2015,5:477-484. (YUE Liangyi, WANG Xuefeng, YOU Yunxiang. A modified hybrid finite-volume/finite-difference scheme for extended Boussinesq-type model [J]. Chinese Journal of Hydrodynamics, 2015,5: 477-484. (in Chinese))

[12] 房克照, 孙家文, 刘忠波, 等. Boussinesq水波方程新型数值解法 [J]. 海洋工程, 2014, 32(2): 97-103. (FANG Kezhao, SUN Jiawen, LIU Zhongbo, et al. Novel numerical solution to Boussinesq wave equations [J]. The Ocean Engineering, 2014, 32(2): 97-103. (in Chinese))

[13] ERDURAN K S, ILIC S, KUTIJA V. Hybrid finite-volume finite-difference scheme for the solution of Boussinesq equations [J]. International Journal for Numerical Methods in Fluids, 2005,49(11): 1213-1232.

[14] 房克照, 王磊, 刘忠波, 等. 基于MUSTA格式的全非线性Boussinesq波浪传播数值模型 [J]. 力学学报, 2014,5: 647-654. (FANG Kezhao, WANG Lei, LIU Zhongbo, et al. A fully nonlinear Boussinesq model for wave propagation based on MUSTA scheme [J]. Chinese Journal of Theoretical and Applied Mechanics, 2014,5: 647-654. (in Chinese))

[15] LE MÉTAYER O, GAVRILYUK S, HANK S. A numerical scheme for the Green-Naghdi model [J]. Journal of Computational Physics, 2010, 229(6): 2034-2045.

[16] KURGANOV A, PETROVA G. A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system [J]. Communications in Mathematical Sciences, 2007, 5(1): 133-160.

[17] YAMAMOTO S, KANO S, DAIGUJI H. An efficient CFD approach for simulating unsteady hypersonic shock-shock interference flows [J]. Computers & Fluids, 1998, 27(5): 571-580.

[18] WANG Y, LIANG Q, KESSERWANI G, et al. A 2D shallow flow model for practical dam-break simulations [J]. Journal of Hydraulic Research, 2011, 49(3): 307-316.

[19] LANNES D, MARCHE F. A new class of fully nonlinear and weakly dispersive Green-Naghdi models for efficient 2D simulations [J]. Journal of Computational Physics, 2015, 282: 238-268.

[20] SYNOLAKIS C E. The runup of long waves [D]. California Institute of Technology, 1986.

[21] DINGEMANS M W. Comparison of computations with Boussinesq-like models and laboratory measurements[R]. Deltares (WL), 1994.

[22] ZHAO B B, DUAN W Y, ERTEKIN R C. Application of higher-level GN theory to some wave transformation problems [J]. Coastal Engineering, 2014, 83: 177-189.

A numerical scheme for one-dimensional and fully nonlinear Green-Naghdi wave equations

JIAO Zifeng1, YIN Jing1, 2, FANG Kezhao1, SUN Jiawen1, 2

(1. The State Key Laboratory of Coastal and Offshore Engineering, Ocean Engineering Joint Research Center of DUT-UWA, Dalian University of Technology, Dalian 116024, China; 2. National Marine Environmental Monitoring Center, State Oceanic Administration, Dalian 116023, China)

O353.2

A

10.16483/j.issn.1005-9865.2016.06.004

1005-9865(2016)06-0030-08

2016-02-01

国家自然科学基金资助项目 (51579034)；中国科学院海洋环流与波动重点实验室开放基金课题资助(KLOCW1502);辽宁省教育厅重点实验室基础研究项目资助(LZ2015013)

焦子峰(1989-)，男，山东日照人，硕士研究生，从事海岸动力学方面研究。E-mail：zfjiao@mail.dlut.edu.cn