雷诺数为3 900时三维圆柱绕流的大涡模拟

2016-10-12端木玉万德成

海洋工程 2016年6期

端木玉，万德成

( 1. 上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心，上海 200240; 2. 江苏海事职业技术学院，江苏南京 212003)

端木玉1,2，万德成1

自从人们对层流的圆柱绕流现象有了系列研究及清楚的认识后，人们逐渐把目光投向湍流的圆柱绕流，但相关研究主要关注于模拟湍流方法的数值格式和精度问题，而忽略了对高雷诺下圆柱绕流流场本身的认识及规律的总结。基于开源代码OpenFOAM的大涡模拟方法以连续方程和Navier-Stokes方程为控制方程，选用Smargorinsky模式为亚格子应力模型，采用有限体积法和一次预测两次修正的PISO算法，对Re=3 900时三维圆柱绕流问题进行了数值模拟研究，并着重分析了其尾流特征和性质。数值计算结果表明：大涡模拟方法可以模拟出细致的流场结构，该雷诺数下的圆柱绕流具有很强的三维及湍流效应，在圆柱后方约一倍直径的范围内存在回流区域，在靠近圆柱壁面的尾流区域的速度剖面呈“U”型，远离壁面的速度剖面呈“V”型。瞬时速度剖面始终围绕着时均速度的周围脉动，且距离圆柱越远瞬时速度场的脉动范围越大。

大涡模拟;圆柱绕流;OpenFOAM;尾流分析

Abstract: After a series of studies of laminar flow around circular cylinders, clear understanding was gained. People then set their sights on turbulent flow problems. However, relevant research mainly focused on the scheme and precision of numerical simulation methods at high Reynolds numbers; less attention was paid to the understanding of turbulent flow around circular cylinders itself. The simulations were carried out using large eddy simulation (LES) solver within the open source code OpenFOAM. The Navier-Stokes equations were discretized by the Finite Volume Method; the Smargorinsky model was chosen as Sub-grid stress model; the PISO algorithm with two prediction steps and one correction step were used to deal with the coupling between velocity and pressure. This paper emphatically analyzes the wake features of the three-dimensional flow around a circular cylinder atRe=3 900. The numerical results show that LES can simulate the detailed flow structures, which exhibit strong three dimensional effects and turbulence effects at the current Reynolds number. The main conclusions of this study are that there exists a recirculation region about one diameter after the cylinder. The mean velocity profile in the region close to the cylindrical wall shows “U” shape, while the velocity profile far from the wall exhibits “V” shape. The instantaneous velocity, which fluctuates around the mean velocity, has a larger amplitude of fluctuation as the distance from the cylinder gets farther.

Keywords: large-eddy simulation; flow past a cylinder; OpenFOAM; wake analysis

圆柱绕流问题一直是流体力学领域非常经典的算例，它能很好地揭示分离流、涡流及脱落过程等复杂流动现象。同时圆柱绕流问题也有很高的工程应用价值，航行中的飞机、水中行驶的船舶、海上的石油平台以及桥墩等，都存在绕流。

在影响圆柱绕流问题的若干影响参数中，雷诺数起着决定性作用。因为湍流具有不规则性、多尺度性及复杂的非线性，所以一直以来有效地描述湍流的性质是流体力学中的一个重大难题。自从人们对低雷诺数下圆柱绕流现象有了系列研究及清楚的认识后，便逐渐把目光投向高雷诺数下的圆柱绕流，如何可以精确描述高雷诺数下圆柱绕流的湍流尾流特征是今后研究工作的重点。湍流状态下的圆柱绕流的尾流表现为高度复杂的三维非稳态、带旋转的不规则的随机流动，圆柱绕流的尾流是由不同尺度漩涡叠合而成的，大尺度的漩涡破裂后形成小尺度的漩涡，小尺度的漩涡也不断溃灭，同时新的漩涡也源源不断产生，这使得研究高雷诺数下的圆柱绕流变得非常困难。

对湍流的模拟常用直接模拟(DNS)、大涡模拟(LES)和雷诺时均(RANS)三种方法。DNS是最精确的方法，但对计算机要求很高，网格必须等于或小于最小漩涡尺寸；LES可选用较大的网格，对超出网格尺寸以上的大尺度湍流进行直接数值模拟，而小于网格尺寸的湍流采用网格内模型来模拟，LES在复杂流动中可以得到RANS无法获得的湍流运动的细微结构和流动现象；RANS抹平了湍流中的微小细节，对复杂精细的湍流结构的模拟会遇到困难。综上所述，LES似乎是目前再现圆柱尾流复杂结构的最佳方法。Breuer[1]采用大涡模拟方法对孤立圆柱绕流问题(Re=140 000)进行了三维的数值模拟，研究了大涡模拟方法对于处理高雷诺数下流动问题的适应性并分析了不同亚格子应力模式及网格质量对结果的影响。Xu等[2]用大涡模拟方法对变截面半径圆柱的可压缩流场进行了数值模拟，分析了波状圆柱绕流与柱状圆柱绕流问题的区别。Lourenco等[3]、Ong等[4]分别对流动条件为Re=3 900的圆柱绕流做过模型试验，并提供了尾涡x/D≤3和3≤x/D≤10处的时均速度场的试验结果，实验只能给出一些时均后的流场参数信息。Breuer[5]用大涡模拟方法计算了Re=3 900下的圆柱绕流，但其目的并不在于研究流场物理现象的细节，而是为分析影响LES精度的数值及模型方面。Kravchenko等[6]也研究了Re=3 900时的圆柱绕流，论证了B样条法是相比于迎风格式和中心差分格式的一种精度更高的数值格式。赵伟文等[7]用大涡模拟方法模拟了高雷诺数三维圆柱Spar的涡激运动问题。王吉飞等[8-9]用大涡模拟方法模拟了高雷诺数三维方腔驱动流问题。

从目前的研究进展来看，虽然已有不少学者对高雷诺数下的圆柱绕流问题做过一些试验及数值研究，但试验的研究很难给出我们所关注的瞬时涡量场、速度场、压力场等信息。而数值研究方面，大多是侧重于分析不同湍流模型或数值格式对计算结果的影响。而针对高雷诺数下圆柱绕流问题这一物理现象展开深入研究的并不多见。鉴于前人对Re=3 900下在试验和数值方面有过诸多贡献，因此本文选取Re=3 900的三维圆柱绕流进行数值研究，不同的是本文侧重于分析该雷诺数下的流场细节，以便了解湍流圆柱绕流问题的尾流特征，并将数值结果与实验结果进行对比，验证并分析数值计算结果的有效性。文中给出了瞬时的涡量场、速度场，分析了流场中特征位置处的流场信息，更进一步分析了瞬时场与速度场之间的关系，使得能深入地理解高雷诺数下圆柱绕流这一物理现象。

数值计算过程采用基于开源程序代码库OpenFOAM平台上的大涡模拟方法，采用有限体积法和一次预测两次修正的PISO算法，以三维不可压缩N-S方程为控制方程。文中选用的OpenFOAM平台，其全称是Open Field Operation and Manipulation，采用C++语言编写的面向对象的计算流体力学开源代码程序库。其支持的流动模型有层流、基于雷诺时均的湍流模型、LES及DNS等；支持多种软件生成的复杂网格及动态网格技术；支持SIMPLE、PISO及PIMPLE求解器。

1 数学模型

1.1 大涡模拟的控制方程

大涡模拟的控制方程是将不可压缩的N-S方程做过滤，得到：

为亚格子尺度雷诺应力(SGS Renolds stress)，则式(1)可写作

建立亚格子应力模式使方程(4)封闭，选用最基本的Smagorinsky模式，其表达形式：

1.2 初始条件和边界条件

本文定义的流场的初始条件和边界条件：

1) 入口，速度入口；

2) 出口，出流边界；

3) 上下面及前后面，对称边界；

4) 圆柱表面，无滑移固壁边界。

2 数值计算与结果讨论

图1 圆柱绕流的几何计算域Fig. 1 Geometry details of flow around a cylinder

采用的计算模型如图1所示，计算域以圆柱底部的中心为坐标原点，圆柱直径D=0.01 m。计算域长度(x轴的方向)为15D，上游断面距离圆柱中心为5D，下游断面距离圆柱中心为15D，方向与来流方向一致；计算域宽度(z轴方向)为πD，方向沿着圆柱方向；计算域高度(y轴方向)为10D，上下面距离圆柱为5D，方向平行于圆柱横截面。入口处为定常来流，流速U0=0.394 m/s，ν=1.01×10-6m2/s，雷诺数Re=U0D/ν≈3 900。首先从网格收敛性方面进行考察，这里选用2套网格，第一套网格总数为792 320，计算域xoy平面网格划分如图2所示，z向均匀划分32层网格，圆柱周围的网格如图3所示。将第一套网格各个区域进行加密后得到第二套网格，第二套网格总数为2 827 500，计算域xoy平面网格划分如图4所示，z向均匀划分50层网格，圆柱周围的网格如图5所示。

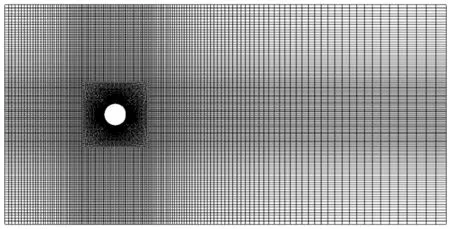
图2 第一套网格计算域xoy平面网格的划分Fig. 2 The first case mesh generation in the xoy plane

图3 第一套网格圆柱周围的网格划分Fig. 3 Mesh in the vicinity of cylinder for the first case

图4 第二套网格计算域xoy平面网格的划分Fig. 4 The second case mesh generation in the xoy plane

图5 第二套网格圆柱周围的网格划分Fig. 5 Mesh in the vicinity of cylinder for the second case

表1 两套网格的数值计算结果Tab. 1 Flow parameters computed by the meshes of the two cases

图6 阻力系数、升力系数的时间历程曲线(Re=3 900) Fig. 6 Time history of the lift coefficient Cl and the drag coefficient Cd

图6给出了Re=3 900时升力和阻力系数的时间历程曲线，可以看出升力系数虽围绕0值上下振荡，但幅值是变化的，与层流情况下的周期性振荡且幅值不变有着显著区别。随着时间的推移，阻力系数没有像层流情况下一样趋于稳定值，而是存在脉动变化，以上都是湍流的显著特征。

图7、8、9分别是圆柱绕流尾流区x、y、z方向上的瞬时速度等值线图。并与贾晓荷[10]的数值模拟结果进行对比，该图中虚线表示u<0，实线表示u>0。由于这里的上下图并非描述的是同一时刻，且速度等值线的划分也不相同，但从上下图的对比可见计算结果的流场特征能够很好地吻合。

在这三幅图中既能看到小尺度的湍流也能看到大尺度的湍流，随着流向距离的增大，流动的结构在尺度上也趋于增大。图7在靠近圆柱的区域存在明显的速度为负值的区域，即回流区，回流区后x向的速度等值线均为正。图8可以看出y方向的瞬时速度有规律的正负交替，且在靠近圆柱的瞬时速度正负交替明显，到远处就逐渐削弱了，说明在圆柱的尾部形成了一系列的卡门涡街，这些漩涡在圆柱附近形成后脱落，漩涡在运动的过程中逐渐扩散开。图9中可以看出z向的速度等值线在圆柱后无规律的正负交错存在，且距离圆柱越远等值线的正负差异越小，说明圆柱后形成的涡随着往后运动而逐渐扩散开来。

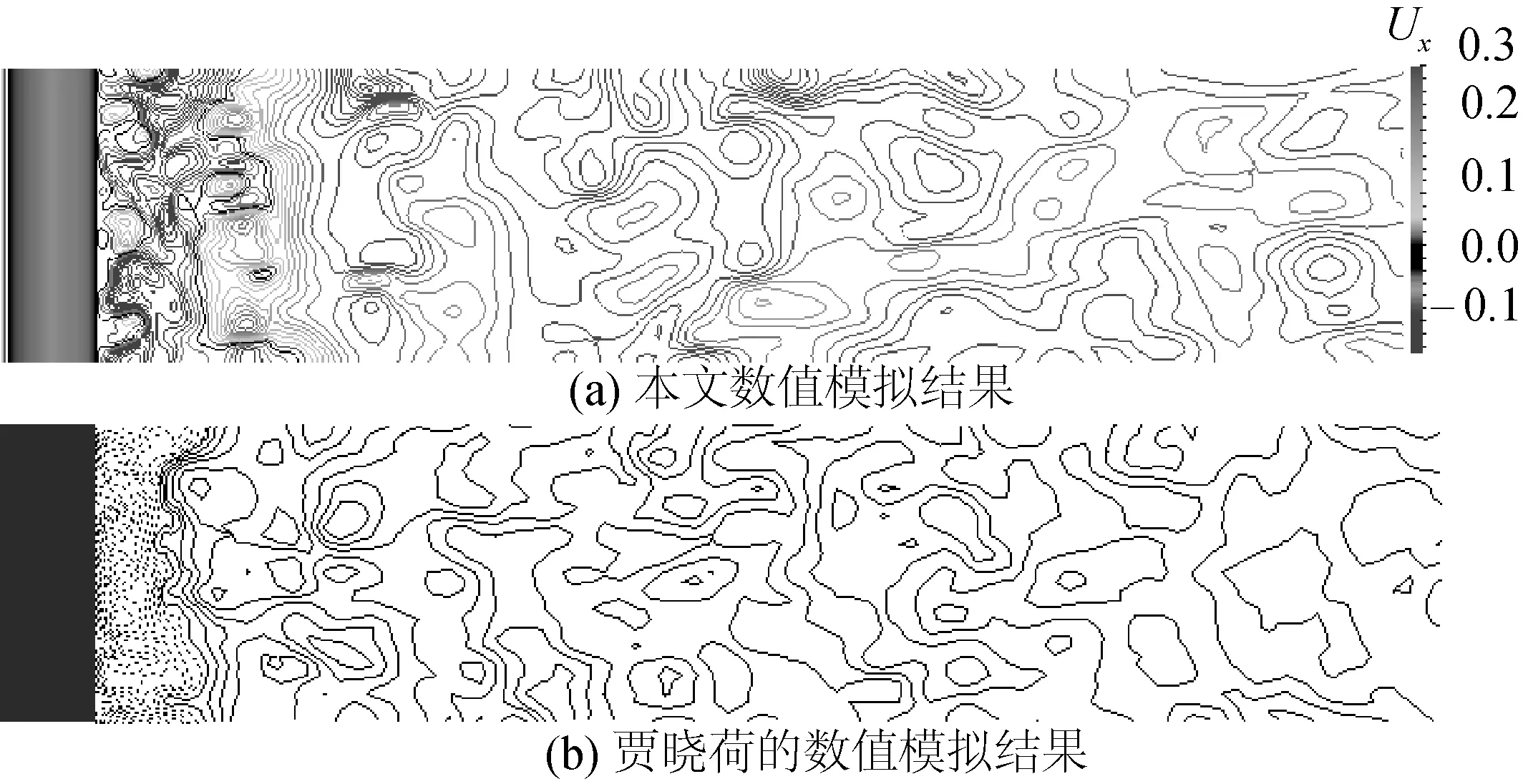
图7 Re=3 900圆柱绕流尾流区x方向的瞬时速度等值线图(x-z平面，y=0)Fig. 7 Instantaneous streamwise velocity in the (x-z, y=0) plane of the presented simulation

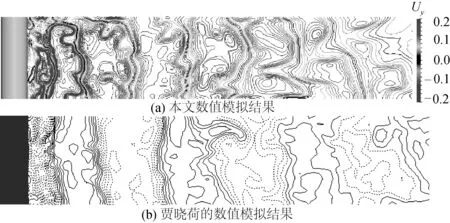
图8 Re=3 900圆柱绕流尾流区y方向的瞬时速度等值线(x-z平面，y=0)Fig. 8 Instantaneous cross-flow velocity in the (x-z, y=0) plane of the presented simulation

图9 Re=3 900圆柱绕流尾流区z方向瞬时速度等值线(x-z平面，y=0)Fig. 9 Instantaneous spanwise velocity in the (x-z, y=0) plane of the presented simulation

图10给出了xoy(z=πD/2)平面处圆柱绕流的涡量等值线图；图11给出了圆柱尾部的瞬时流场涡量，图中的涡量等势面用Hunt等人[15]建议的Q准则(Q-criterion)表示。Q的定义如下：

图10与图8的叙述也是吻合的，可以更加直观的看出漩涡在圆柱附近形成后脱落，并且漩涡在运动的过程中逐渐扩散开。但是Re=3 900时形成的涡街与低雷诺数的情况存在明显的差异，低雷诺数时通常观察到物体尾流左右两侧产生成对的、交替排列的、旋转方向相反的反对称涡旋，漩涡的脱落过程具有非常的规律性，循环往复。Re=3 900的工况下，每个瞬时在圆柱尾部的一侧会有不同大小的多个漩涡脱落，随后向中心线移动，移动的过程中漩涡的尺度逐渐增大并直至脱落，虽然整个过程都是在圆柱两侧交替生成漩涡并逐渐脱落的过程，但每一次漩涡生成及脱落的过程都不是完全相同的，存在一定的随机性。图11展示了Re=3 900下圆柱绕流的尾流呈现明显的湍流及三维特性，涡面上的深色及浅色分布代表了相反的旋涡旋转方向。

图10 xoy (z=πD/2)平面处涡量等值线图Fig. 10 Contours of instantaneous vorticity magnitude in the (x-y,z=πD/2) cross-sectional plane

图11 瞬时的三维涡量等值面图(Q=100) Fig. 11 Isosurface of instantaneous vorticity magnitude (Q-criterion, Q=100)

表2不同长细比圆柱绕流的流场参数与前人工作的对比

Tab.2Theparametersoftheflowaroundthecylinderwithdifferent-aspectratioandcomparedtoexistingresultsintheliterature

算例长细比St数基础吸力系数平均阻力系数回流区长度-umin/U¥CaseA112π0.21510.84991.14761.7540.243CaseA2π0.21540.92631.13561.4170.325CaseA32π0.21910.93761.11491.3600.355Lysenko[12]:LESwithSMAGπ0.190.81.180.90.26Lysenko[12]:LESwithTKEπ0.2090.910.971.670.27Norberg[13]150-0.875---Norberg[13]26-0.78---LourencoandShih[3]20.50.22-0.991.220.247KravchenkoandMoin[6]2π0.210.941.04-0.35

图12分别给出了同一时刻，相同涡量等势面的瞬时三维涡量图(俯视图)。从图中可见，展向的长度越长，圆柱尾流处的漩涡相对越加紊乱，漩涡尺度也相对较小一些，但这种差别并不是十分明显。另外一个特征是对于展向长度较长的圆柱，漩涡要早于展向长度短的圆柱脱落。

(b) 圆柱展向长度为πD

(c) 圆柱展向长度为πD图12 不同圆柱展向长度下的瞬时三维涡量等值面图(Q=100)Fig. 12 Isosurface of instantaneous vorticity magnitude in the wake of a cylinder with axial length (Q-criterion, Q=100)

为便于与实验结果进行对比以显示圆柱周围近尾流区及远尾流区的流场特征，现将圆柱附近的特征位置描述如图13所示。所取的截面是xoy(z=πD/2)处的平面，y/D=0是该平面上从圆柱中心沿x轴正方向到x=15D处的直线，x/D=0.58,1.06,1.54,2.02是该平面上与y轴平行的直线，直线的范围是-3.0D～3.0D。

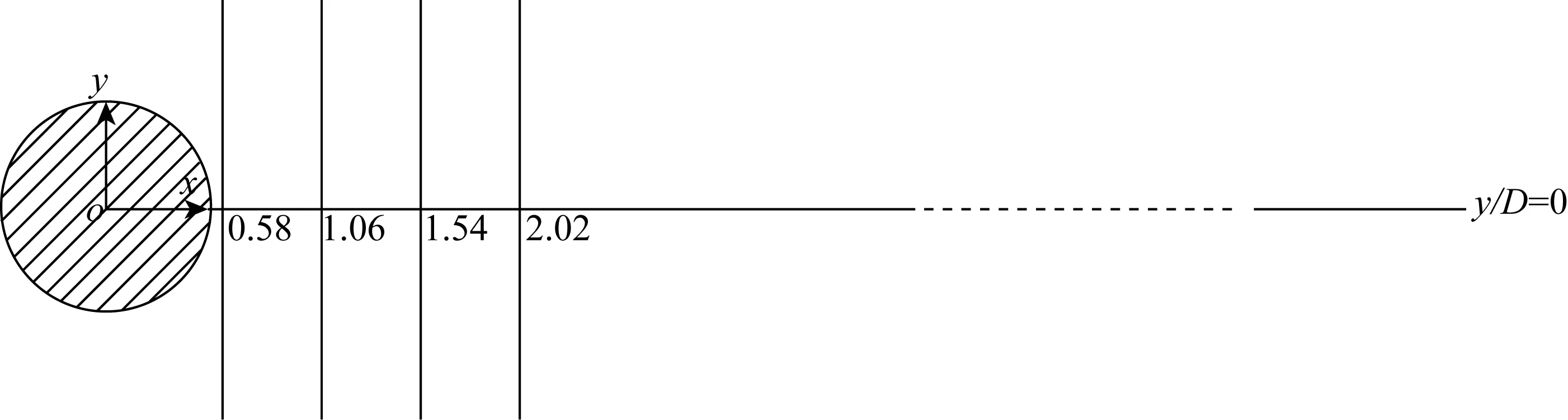
图13 圆柱周围的特征位置Fig. 13 The characteristic locations near the cylinder

图14是圆柱中心线y/D=0上x方向的平均流速分布。将数值计算结果与Lourenco等[3]及Ong等[4]的实验结果及Kravchenko等[6]的数值结果进行对比，模拟出的趋势和实验结果完全吻合，数值模拟的精度也较Kravchenko等[6]更接近于实验值。从图中发现在圆柱后面约1个直径的范围内平均速度为负值，该范围是回流区域，这与前面图7的描述是一致的。回流区的范围与实验值很接近，但是平均速度值较实验值偏大一些，这可能是由于实验存在外界扰动，从而导致近圆柱处尾流速度的提前过渡。

图14 圆柱中心线y/D=0上x方向的时均流速分布Fig. 14 Streamwise mean velocity on the center line in the wake of a cylinder

图15分别给出了x/D=0.58,1.06,1.54,2.02处x方向一系列瞬时的速度剖面及时均速度。这里共列出了37个瞬时的x速度剖面，时间间隔ΔT=0.02s，用浅色的线表示，深色的线是这37个速度剖面的平均值。从图中可见瞬时速度剖面始终围绕着时均速度的周围脉动，且距离圆柱越远脉动的范围越大，因为距离圆柱越远的地方物体对流体的控制越弱。时均速度剖面在所取的四个特征位置处的形状也有其特征，平均速度的谷值一定在y/D=0的中心线上，但是各瞬时的谷值围绕中心线振荡。x/D=0.58处的时均速度呈“U”型，其余呈“V”型，随着距离的增大，“V”的形状也趋于平缓。在x/D=0.58处及x/D=1.54处的时均速度的谷值都接近于0，在x/D=1.06处的时均速度谷值在负值最大处，而在x/D=2.02处的时均速度谷值为正，以上这些特征都和图14相符。

(a) x/D=0.58

(b) x/D=1.06

(d) x/D=2.02

图16 圆柱尾流在4个特征位置处x方向的时均速度分布 Fig. 16 Profiles of streamline mean velocity at four locations downstream of a cylinder

将上述四个特征位置处x方向的时均速度值与实验值进行对比，如图16所示。数值计算结果的趋势与Lourenco & Shih[3]的实验结果完全吻合，距离圆柱越近的位置与实验结果越相近，距离圆柱越远的地方则有较大误差。

图17分别给出了x/D=1.06,1.54,2.02处y方向一系列瞬时的速度剖面及时均速度。同上一样共列出了37个瞬时的x速度剖面，时间间隔ΔT=0.02s，用浅色的线表示，深色的线是这37个速度剖面的平均值。

图17 不同x/D条件下y方向的瞬时速度和时均速度Fig. 17 Profiles of cross-flow velocity at different x/D position

将上述三个特征位置处y方向的时均速度值与实验值进行对比，如图18所示。从图中可见所有y向平均速度剖面的形状均关于y/D=0反对称，与实验的趋势基本吻合，数值上存在一定误差。

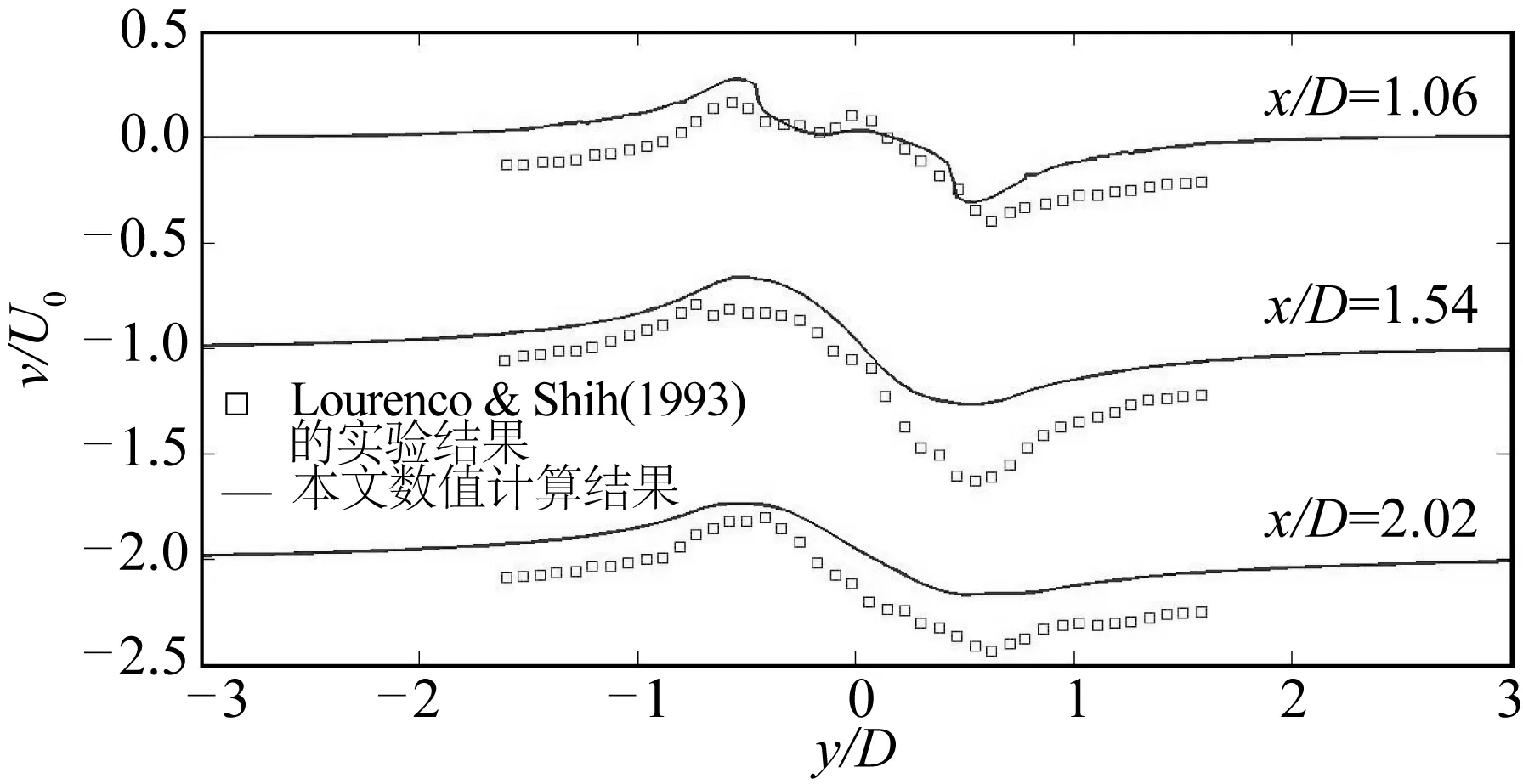
图18 圆柱尾流在3个特征位置处y方向的时均速度分布Fig. 18 Profiles of cross-flow mean velocity at three locations downstream of a cylinder

3 结语

基于OpenFOAM的大涡模拟方法研究了Re=3 900时圆柱绕流问题，并对数值模拟结果进行了分析，得到以下结论：

1) 在雷诺数较高的情况下必须采用三维的计算模型，二维简化模型会对计算结果产生较大误差，且在较高雷诺数下，圆柱绕流的漩涡脱落已经具有了三维效应；

2) 从升力系数和阻力系数的时历曲线中可以明显看出存在明显的脉动，无特征规律可循，说明在Re=3 900时已经存在明显的湍流效应，另漩涡脱落的过程也说明了湍流效应；

3)Re=3 900的工况下，每个瞬时在圆柱尾部的一侧会有尺度不同的多个漩涡脱落，随后向中心线移动，移动的过程中漩涡的尺度逐渐增大并直至脱落，且每一次漩涡生成及脱落的过程都不是完全相同的，存在随机性；

4) 数值模拟出的St=0.222，换算得漩涡脱落的频率fst=8.75 Hz；

5) 在靠近圆柱尾部约1D的范围内是回流区，之后沿x方向速度逐渐增大，并趋于平衡；

6) 对圆柱后x/D=0.58,1.06,1.54,2.02的四个特征位置处的流场进行了分析，所有x向时均速度剖面的形状均关于y/D=0对称，x/D=0.58处的时均速度呈“U”型，其余呈“V”型，且随着距离的增大，“V”的形状也趋于平缓。瞬时速度剖面始终围绕着时均速度的周围脉动，且距离圆柱越远瞬时速度场的脉动范围越大，这是因为距离圆柱越远的地方物体对流体的控制越弱。

[1] BREUER M. A challenging test case for large eddy simulation: high Reynolds number circular cylinder flow [J]. Heat and Fluids Flow, 2000, 21: 648-654.

[2] XU Changyue, CHEN Liwei, LU Xiyun. Large-eddy simulation of the compressible flow past a wavy cylinder[J]. Journal of Fluid Mechanics, 2010, 665: 238-273.

[3] LOURENCO L M, SHIH C. Characteristics of the plan turbulent near wake of a circular cylinder: A partical image velocimetry study[R]. Private Communication, 1993.

[4] ONG L, WALLACE J. The velocity field of the turbulent very near wake of a circular cylinder[J]. Experiments in Fluids, 1996, 20: 441-453.

[5] BREUER M. Large eddy simulation of the subcritical flow past a circular cylinder: numerical and modeling aspects[J]. International Journal For Numerical Methods in Fluids, 1998, 28: 1281-1302.

[6] KRAVCHENKO A G, MOIN P. Numerical studies of flow over a circular cylinder atReD=3 900[J]. Physics of Fluids, 2000, 12(2):403-417.

[7] 赵伟文，万德成. 用大涡模拟方法数值模拟Spar平台涡激运动问题[J]. 水动力学研究与进展，2015, 30(1): 40-46. (ZHAO Weiwen, WAN Decheng. Numerical investigation of vortex-induced motions of Spar platform based on large eddy simulation [J]. Chinese Journal of Hydrodynamics, 2015, 30(1): 40-46. (in Chinese))

[8] 王吉飞，万德成.三维顶板斜向驱动方腔流的有限元并行计算[J]. 海洋工程，2015, 33(2): 1-12. (WANG Jifei, WAN Decheng. Parallel simulation of 3D lid-driven cubic cavity flows at yaw by finite element method [J]. The Ocean Engineering, 2015, 33(2): 1-12. (in Chinese))

[9] WANG Jifei, WAN Decheng. Parallel finite element method for 3D lid-driven cubic cavity flows[J]. International Journal of Offshore and Polar Engineering, 2014, 24(2): 106-113.

[10] 贾晓荷,单圆柱及双圆柱绕流的大涡模拟[D]. 上海：上海交通大学，2008. (JIA Xiaohe. Large eddy simulation of flow around one and two circular cylinders [D]. Shanghai: Shanghai Jiao Tong University, 2008. (in Chinese))

[11] WELLER H G, TABOR G, JASAK H, et al. A tensorial approach to computational continuum mechanics using object-oriented techniques [J]. Computers in Physics, 1998, 12(6): 620-631.

[12] LYSENKO D A, ERTESVåG I S, RIAN K E. Large-eddy simulation of the flow over a circular cylinder at reynolds number 3 900 using the OpenFOAM toolbox [J]. Flow, Turbulence and Combustion, 2012, 89(4): 491-518.

[13] NORBERG C. Effects of Reynolds number and low-intensity free stream turbulence on the flow around a circular[R]. Gothenburg: Chalmer University of Technolgy, 1987.

[14] WORNOM S, OUVRARD H, SALVTTI M V, et al. Variational multiscale largeeddy simulations of the flow past a circular cylinder: Reynolds number effects [J]. Comput. Fluids, 2011, 47(1), 44-50.

[15] HUNT J C R, WRAY A A, MOIN P. Eddies, streams and convergence zones in turbulent flows [R]. Center for Turbulence Research Report CTR-S88, 1988: 193-208.

Large-eddy simulation of the flow past a cylinder with Re=3 900

DUAN Muyu1, 2, WAN Decheng1

(1. State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China; 2. Jiangsu Maritime Institute, Nanjing 212003, China)

O351.2

10.16483/j.issn.1005-9865.2016.06.002

1005-9865(2016)06-0011-10

2015-10-28

国家自然科学基金项目(51379125，51490675，11432009，51411130131)；长江学者奖励计划(2014099)；上海高校特聘教授(东方学者)岗位跟踪计划(2013022)；工信部高技术船舶数值水池创新专项课题(2016-23/09)

端木玉(1981-),博士研究生，主要从事海洋工程水动力学方面研究。

万德成。E-mail：dcwan@sjtu.edu.cn