动力扰动对充填体稳定性影响的数值模拟研究

吕富强，罗黎明，李爽

（1.湖南新龙矿业有限责任公司六三零工区，湖南邵阳422000；2.中南大学资源与安全工程学院，湖南长沙410083）

动力扰动对充填体稳定性影响的数值模拟研究

吕富强*1，罗黎明2，李爽2

（1.湖南新龙矿业有限责任公司六三零工区，湖南邵阳422000；2.中南大学资源与安全工程学院，湖南长沙410083）

充填体的稳定性分析对二步骤矿房回采具有重要的意义。数值模拟方法是岩体动力响应研究的有效方法之一。根据云南某矿山工程实际，利用Midas/GTS与FLAC3D软件建立了三维数值模型，采用FLAC3D软件对充填体的动力稳定性进行了数值分析，并对不同扰动强度下充填体的动力响应规律进行了研究。得到动力扰动作用下充填体的破坏方式与破坏区域发展过程及不同扰动强度下充填体的力学响应。

充填体；稳定性分析；数值模拟；动力响应

1　概述

随着中国工业化进程及浅地表矿产资源的开发深井开采已经成为矿山开采的必然趋势［1-2］。充填采矿法能够有效控制深井岩爆提高深部资源回收率30%～40%，已广泛应用于深井矿山开采。稳定的充填体是二步骤矿房回采的安全保障，然而目前对于充填体的稳定性分析主要集中在静力分析，而实际上，不管是采空区围岩还是充填体，在承受静压的同时还会受到爆破产生的动力扰动，因此在采矿动力作用下实现充填体的稳定性预测具有重要的意义。

国内外许多学者对动力扰动作用下矿柱、采空区围岩以及巷道等的力学响应和稳定性进行了深入研究，如李夕兵［3］等采用FLAC3D软件对深井高应力矿柱在动力扰动下的三维动态力学行为进行了研究，认为外界较小强度的扰动都可能诱发深部承受极高初始静载的矿柱产生塑性破坏；朱万成［4］等对深部巷道工程围岩在动态应力作用下发生的破裂过程利用数值软件系统RFPA进行了分析，认为动态扰动导致巷道破坏与其所处的地应力状态息息相关；闫长斌［5］等同对爆破载荷作用下采空区的围岩状况运用FLAC3D进行了数值模拟分析，认为爆破震动波形对围岩位移分布有极大地影响。但对充填体的动态响应及其动力稳定性分析研究较少。本文以云南某矿为背景，利用FLAC3D软件对充填体的动力稳定性进行数值模拟分析，旨在揭示动力扰动下充填体的力学响应及扰动强度对充填体失稳破坏的影响效果，为深部二步骤矿房回采提供安全保障。

2　三维数值模型与参数选取

2.1三维数值计算模型

某矿山分段空场嗣后充填采矿方法试验矿段，采用隔一采一的开采方式，一步骤采场开采完毕后，随即进行胶结充填，之后开采二步骤采场，二步骤采场开采时两侧均为充填体。典型采场长度为20m，高度为20m，宽度为矿体总宽度约10～30m。采用Midas/GTS与FLAC3D构建三维数值模型，计算模型如图1所示：采场尺寸长、宽、高分别为20m×20m×20m，矿体倾角取45°。

2.2岩体物理力学参数的选取

数值计算中，材料模型采用理想弹塑性模型，屈服准则采用Mohr-Coulomb强度准则，岩体物理力学参数如表1所示。

2.3动力荷载的施加

岩体开挖时爆破动力、地震波等类似动力扰动在数值计算时可取载荷波形中为谐波的一段，数学表达式为式（1）［6］。

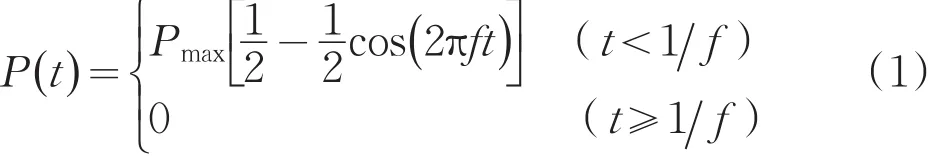
式中：Pmax——扰动应力峰值；

f——动力作用频率。

冲击波、应力波和地震波在传播时具有不同的应力幅值，这也是它们具有不同的衰减速率和作用范围的原因［7-8］。应力波的衰减规律与冲击波的衰减规律相同，由此可以得出出炮孔内的初始径向峰值压力等效到弹性震动圈上的等效压力为：

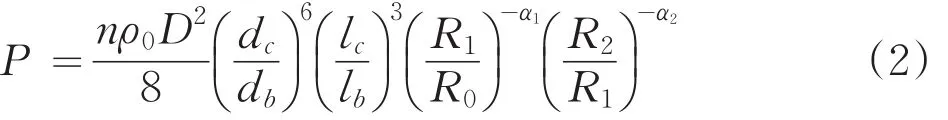
式中：P——弹性震动圈上的等效压力；

R0——炮孔半径；

R1——距炮孔中心的距离；

R2——裂隙区半径；

α1、α2——冲击波和应力波衰减指数；

ρ0——炸药密度；

D——爆速；

dc——炮孔直径；

db——装药直径；

lc——炮孔长度；

lb——装药长度；

n——压力膨胀系数。

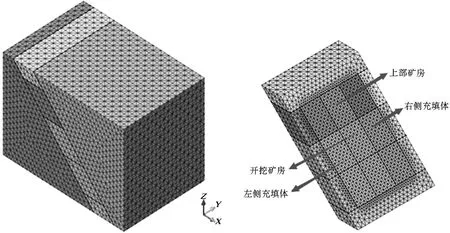
图1　充填体动力响应三维数值分析模型

表1　岩体物理力学参数

根据式（2）以及表2中参数计算得到动力扰动幅值为5.46～15.9MPa。

表2　炸药及爆破参数

为了分析不同扰动强度下充填体的动力响应规律，取振动频率f=25Hz，动载荷持续作用时间40ms，计算求解时间取0.3s（计算表明0.3s后充填体力学响应基本完成）。扰动应力Pmax分别为6MPa、8MPa、10MPa、12MPa、14MPa、16MPa，加载波形如图2所示。

在充填体暴露面及内部关键部位设置特征监测点，旨在揭示开挖过程中和动荷载作用下充填体的振动特性规律，从而更有效地表征关键部位岩体的稳定程度。监测点布置如图3所示。

2.4动力阻尼的确定

在对岩体进行动力响应分析时，通常引入阻尼来模拟真实岩石节理体系受动荷载作用时的能量衰减过程［9］。本次模拟选用瑞利阻尼进行计算，模拟中临界阻尼比通过试算确定为0.05，中心频率通过对模型进行无阻尼条件下的自振反应分析确定为12.6Hz。

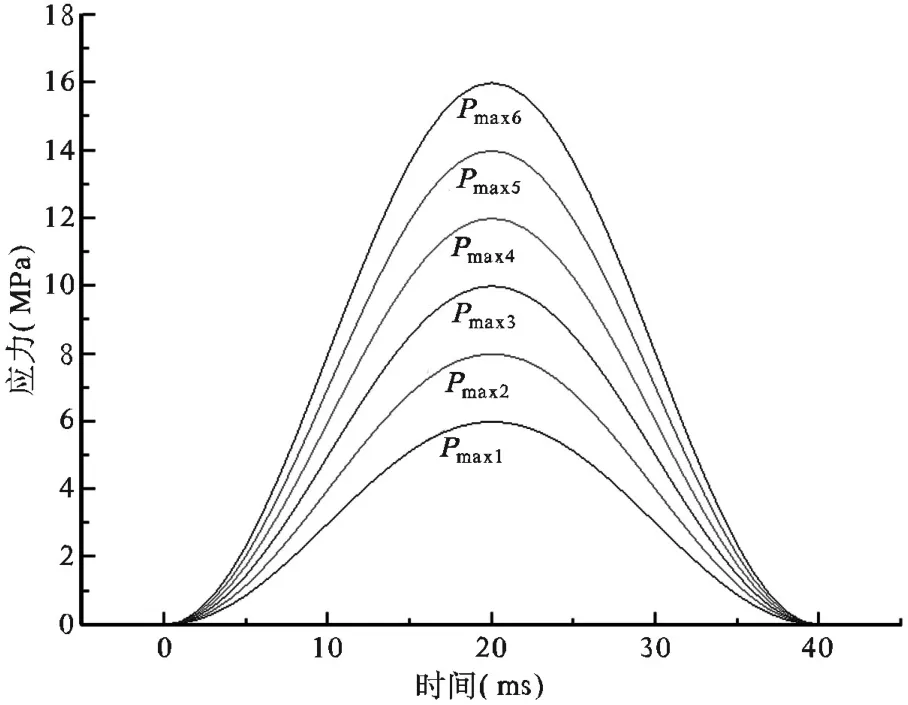
图2　不同扰动强度加载曲线

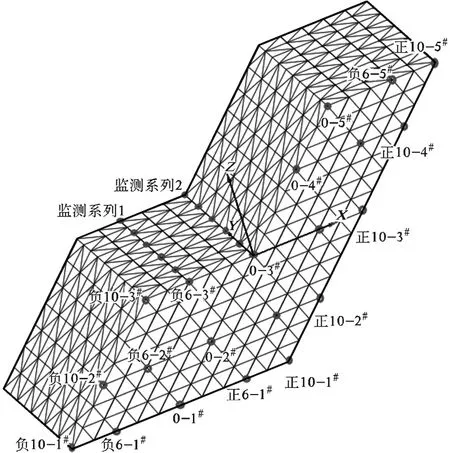
图3　左侧充填体上监测点布置示意图

3　数值模拟结果与分析

3.1最大最小主应力分析

通过分析岩体最大、最小主应力，研究岩体在不同动力幅值扰动下的应力变化规律及破坏形式。

充填体与上中段矿体最大主应力主要以压应力形式呈现，仅有小部分区域承受极小的拉应力。压应力较大的区域主要出现在：充填体暴露面四周。由于矿体抗压强度远大于其所承受的压应力，因此，重点分析充填体压应力较大区域的应力状态。

在6MPa扰动幅值时暴露面四周压应力值已达到3～4.2MPa，在充填体暴露面下部会出现压破坏，但是影响范围较小；在12MPa扰动幅值时，暴露面四周压应力值已达到4～6.9MPa，即在充填体暴露面一侧大部分区域会出现压破坏，且在距充填体暴露面1m左右范围内，压应力达到3～4MPa，部分充填体会塌落；在16MPa扰动幅值时，暴露面大部分区域压应力值在4～9.7MPa范围内，而在距充填体暴露面2m左右范围内，压应力达到3～6MPa，破坏范围加大。即随着扰动幅值的增加最大主应力也逐渐增加，刚开始破坏主要出现在充填体暴露面下部，但是随着动力扰动峰值的增加，充填体暴露面大部分区域均会出现破坏，而且破坏区域逐渐扩大到距充填体暴露面2m左右。

充填体与上中段矿体第三主应力出现拉应力与压应力共存，在充填体暴露面上除中心区域之外均处于压应力状态，在充填体上下端面靠近充填体暴露面处也处于压应力状态，但是压应力值较小。由于充填体抗拉强度较小，故重点分析充填体是否会产生拉破坏。

在动力扰动幅值为6MPa时，在充填体暴露面上下部会出现拉应力集中现象，其它地方拉应力较小只有0～0.75MPa，小于充填体动态抗拉强度1.4MPa。在动力扰动幅值为12MPa时，充填体大部分区域承受0～1MPa拉应力，整体上不会失稳；但是在充填体暴露面四周以及充填体与下盘围岩交界处两侧会产生1～2.4MPa拉应力，部分区域会产生破坏，破坏范围可达到距充填体两侧1m左右。在动力扰动幅值为16MPa时，在充填体暴露面与下盘围岩交界面两侧拉应力达到1.25～2.6MPa，交界面两侧大部分区域会产生拉伸破坏。也就是说当扰动峰值较小时只在充填体暴露面上下部产生局部破坏；当应力峰值逐渐增加时在充填体暴露面四周以及充填体与下盘围岩交界处两侧会产生拉伸破坏；当扰动幅值增加到16MPa时，在充填体暴露面与下盘围岩交界面两侧大部分区域会产生拉伸破坏。

3.2应力时程曲线分析

由于主应力云图只能显示岩体在某一时刻的应力状态，无法表征岩体的应力变化过程，为了揭示充填体在动力扰动下的应力变化规律，在充填体暴露面上选取正6-1#至正6-5#共5个监测点，记录得到最大、最小主应力随时间的监测曲线，如图4、图5所示。

由图4、图5可知：正6-2#、正6-3#、正6-4#监测点所在单元最大、最小主应力均为压应力，随着动力扰动幅值从6MPa增加到16MPa，单元最大、最小主应力增大到峰值后，在系统阻尼作用下开始衰减，最终都能恢复到初始静载平衡状态，且并未超过充填体的极限承载能力，这说明这些单元在动力扰动影响下均处于弹性状态，并未发生塑性破坏。同时通过对比各图可知：上述监测单元的最大、最小主应力的峰值均随着动力扰动幅值的增加出现相应的增大。

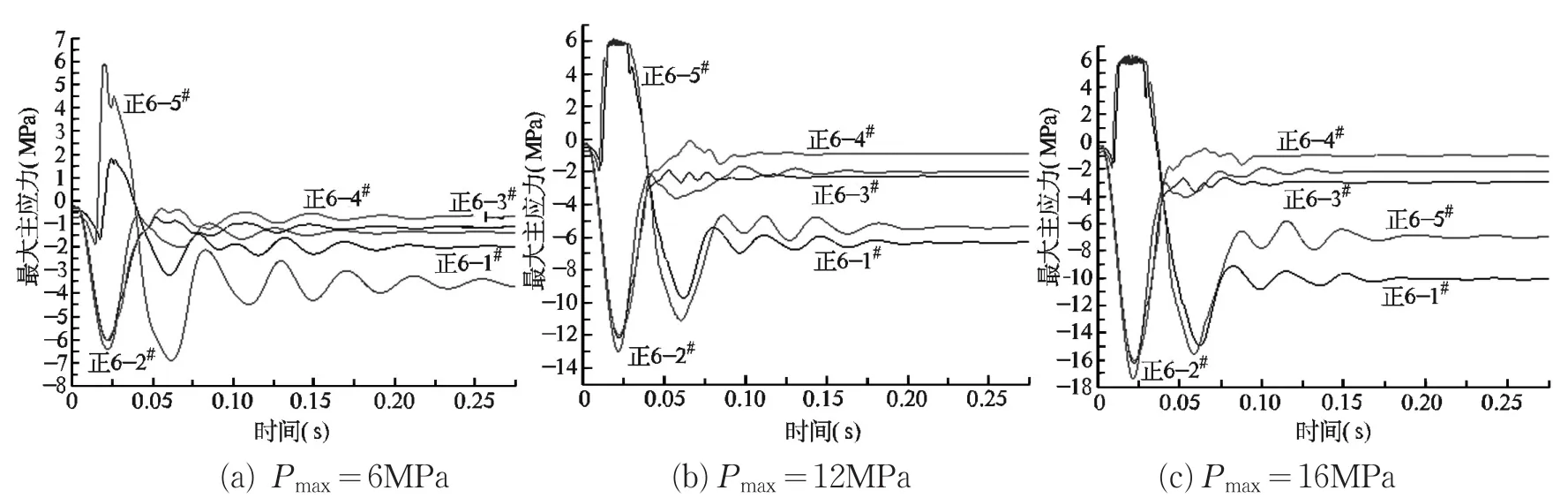
图4　充填体暴露面监测单元最大主应力变化曲线

图5　充填体暴露面监测单元最小主应力变化曲线

充填体暴露面上正6-1#、正6-5#监测点所在单元最大主应力为压应力，最小主应力为拉应力。在6MPa、8MPa峰值扰动强度时，最大主应力时程曲线波形完整，且最终状态下最大主应力均小于4MPa，因此不会发生压破坏；但从其最小主应力时程曲线可知，单元所受拉应力已超过其承载强度，会产生拉伸破坏。随着动力扰动幅值的增加，正6-1#、正6-5#监测单元的最大最小主应力峰值已不再增加，应力时程曲线呈现出一种波动状态。从单元最终所承受的应力值大小即可确定上述单元已经发生破坏，主要为压剪破坏。此结论与之前分析在充填体暴露面上下部会出现较大的压应力、拉应力集中现象相吻合。

4　结论

（1）利用Midas/GTS与FLAC3D软件建立了三维数值模型，采用FLAC3D软件对充填体的动力稳定性进行了数值分析，并对不同扰动幅值下充填体的动力响应规律进行了研究。

（2）不同扰动幅值下应力分布规律基本相似，压应力较大的区域主要出现在采空区暴露面四周，最大压应力随着扰动幅值的增加从4.19MPa增加到10MPa左右。充填体的破坏主要从暴露面四周开始破坏，然后逐渐向内部扩展。随着扰动幅值的增加，破坏范围可逐渐扩大到距充填体暴露面2m左右。这也说明：在矿房回采时应尽可能使用小药量微差爆破，减小动力扰动的幅值，可以降低对两侧充填体的影响。

［1］李夕兵，刘志祥，彭康，等.金属矿滨海基岩开采岩石力学理论与实践［J］.岩石力学与工程学报，2010，29（10）：1945-1953.

［2］魏明尧，王恩元，刘晓斐，等.动力扰动诱发顶板断裂的数值模拟分析［J］.采矿与安全工程学报，2010，27（4）：533-536.

［3］李夕兵，李地元，郭雷，等.动力扰动下深部高应力矿柱力学响应研究［J］.岩石力学与工程学报，2007，26（5）：922-928.

［4］闫长斌，徐国元，李夕兵.爆破震动对采空区稳定性影响的FLAC3D分析［J］.岩石力学与工程学报，2005，24（16）：2894-2899.

［5］温颖远，牟宗龙，易恩兵，等.动力扰动下不同硬度煤层巷道围岩响应特征研究［J］.采矿与安全工程学报，2013，30（4）：555-559.

［6］林国洪.基于ANSYS和GeoStudio耦合的充填体底板稳定性分级［J］.有色金属科学与工程，2014（3）：91-95.

［7］胡建华，雷涛，周科平，等.充填环境下预裂缝的爆破动力响应分析［J］.中南大学学报：自然科学版，2011（6）：1704-1709.

［8］曹安业.采动煤岩冲击破裂的震动效应及其应用研究［D］.中国矿业大学矿业工程学院，2009.

［9］张玉成，杨光华，刘鹏，等.爆破荷载在数值计算中的等效施加方法研究［J］.地下空间与工程学报，2012，8（1）：56-64.

TD853.34

A

1004-5716（2016）10-0133-04

2015-11-23

2015-11-25

吕富强（1983-），男（汉族），湖南株洲人，助理工程师，现从事中小型矿体开采方法的工作。