一种振动信号的EMD去噪方法及其仿真分析
2016-10-12李永军崔心瀚
李永军 崔心瀚 李 珂
(军械工程学院导弹工程系,河北 石家庄 050003)
一种振动信号的EMD去噪方法及其仿真分析
李永军崔心瀚李珂
(军械工程学院导弹工程系,河北 石家庄050003)
针对在集合经验模态分解(EEMD)降噪应用过程中出现的模态混叠问题,采用排列熵与经验模态分解(EMD)相结合的方法,对振动信号进行降噪。引入排列熵概念,利用排列熵对EEMD分解得到的固有模态函数(IMF)进行随机性检验,形成新的EEMD降噪处理方法。仿真试验结果表明,该方法能有效提高信噪比,运算效率也得到了较大程度的提升。
经验模态分解(EMD)集合经验模态分解(EEMD)辅助噪声降噪模态混叠IMF排列熵仿真
0 引言
非平稳、非线性信号的降噪处理,是信号处理中的一个难题。研究人员曾尝试采用经验模态分解(empirical mode decomposition,EMD)方法,对含噪信号进行降噪。由于模态混叠等问题,导致EMD对包含间断信号以及脉冲干扰的含噪信号降噪效果不甚理想[1-3]。集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法的出现,为解决EMD降噪问题提供了新的解决思路。
本文在分析EEMD方法降噪基本原理的基础上,采用了一种基于改进EEMD的振动信号降噪处理方法。该方法结合EEMD在处理模态混叠问题上的突出表现,引入排列熵作为信号异常事件检测标准,判断辅助噪声添加截止条件,从而完成非平稳、非线性振动信号的降噪处理。
1 EEMD分解
为了有效抑制模态混叠影响,有学者结合白噪声频谱均匀分布的特性,借助白噪声有效调节不同时间尺度信号分布[4],在EMD研究的基础上,提出了EEMD方法。通过向信号添加白噪声的方式,平滑间断信号和脉冲干扰,并利用白噪声零均值特性,经过多次平均计算抵消噪声余量,进而达到抑制模态混叠、还原信号特征信息的目的[3]。EEMD本质上是一种叠加高斯白噪声的多次经验模态分解,其算法具体步骤如下。
①向待分析信号x(t)中分别加入n(n>1)次均值为零、幅值标准差为常量的高斯白噪声ni(t),得到新的待分析信号xi(t):
xi(t)=x(t)+ni(t)
(1)
②对xi(t)进行EMD分解,将得到的固有模态函数(intrinsic mode function,IMF)分量记为cij(t),cij(t)表示第i次添加高斯白噪声进行EMD分解得到的第j个IMF分量。
③利用不相关随机序列统计值为零的原理,对得到的IMF分量进行总体平均计算,抵消多次加入高斯白噪声对IMF分量真实性的影响,最终得到EEMD分解后的IMF分量:
(2)
2 改进EEMD的降噪方法
当原信号去除异常信号后,如果继续添加白噪声信号,将产生两个问题[5-6]:一是人为增加了EEMD分解及计算的工作量;二是会产生更多的虚假分量。为了更加高效地完成EEMD分解,引入排列熵(permutation entropy,PE)的概念,利用排列熵对EEMD分解得到的IMF随机性进行检验。
改进算法的基本思想为:在EEMD分解过程中,产生的高频分量和异常分量的随机性相对较大,因此对应的排列熵值较大,并且会被率先分解;低频分量分布规则且随机性较小,多为平稳信号,其对应排列熵较小,分解出现位置靠后。利用这种随机性大小的差异,通过对不同分解排列熵阈值的有效设置,能够减小或避免EEMD方法中不必要高斯白噪声的添加。
首先引入排列熵概念,并在此基础上引入EEMD降噪方法。
(1)排列熵。
排列熵由Bandt等人[7]提出,作为近些年兴起的一种衡量一维时间序列随机性和检测动力学突变的方法。在一维时间序列随机性处理的性能上,排列熵与传统手段Lyapunov指数以及分形维数等相比,效果相近并且计算效率更高[8],因此,选择排列熵对EEMD分解得到的IMF分量进行随机性检验。其计算步骤如下。
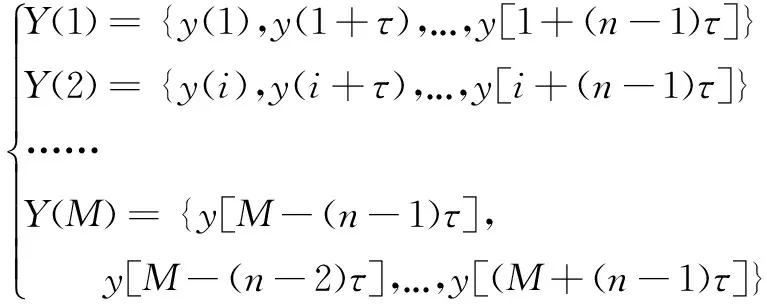
(3)
式中:n为时间序列嵌入维数;τ为时间延时量。
对时间序列Y(i)的n个向量按照升序重新排列,具体操作如下:
Y(i)={y[i+(w1-1)τ]≤y[i+(w2-
1)τ]≤……≤y[i+(wn-1)τ]}
(4)
在对时间序列进行重新排列的过程中,经常会出现y[i+(wi1-1)λ]=y[i+(wi2-1)λ]的情况。对于这种情况的处理,通过比较i1和i2的大小进行排序,简单而言就是当i1 y[i+(wi1-1)λ]≤y[i+(wi2-1)λ] (5) 这样,对于任一时间序列,都能得到一组符号序列: H(q)=[i1,i2,…,im] (6) 式中:q=1,2,…,l,l满足条件l≤m!。 序列符号H(q),是相空间通过映射得到m!个符号序列中的一个,每一个符号序列的概率和为1。 时间序列排列熵的计算,可借用Shannon熵的形式: (7) Sp=Sp(m)/ln(m!) (8) 经过标准化处理的排列熵值Sp被严格控制在[0,1]之间,排列熵值Sp的大小反映时间序列的随机程度。Sp越大,则对应的时间序列随机性越强;Sp越小,则对应的时间序列周期性越强[9]。 在排列熵计算过程中,相关参数选择合适与否将直接影响到最终信号的随机性判断,因此必须选择合适的时间序列长度L、嵌入序列维数m和时间延迟[10]。 为了选择最佳的时间序列长度L,选择长度为128、256、512、1 024、2 048和4 096点的随机信号,分别计算对应的排列熵,结果如图1所示。从图1可以看出,当信号长度大于1 024点时,排列熵值随序列长度变化就不再明显。因此,序列长度选择1 024点比较合适。 对于嵌入序列维数m,Bandt等认为最佳范围在3~7之间。若m取值过小,序列包含状态过少不足以支撑算法的有效性;若m取值过大,序列空间的重构会产生均匀化处理的现象,无法检测序列的微小变化;同时,排列熵的计算量也将大幅度增加[5]。 与时间序列L和嵌入维数m对参数变化范围的特殊要求相比,时间延迟τ对信号排列熵值的影响相对较小。考虑到计算效率,一般情况下,时间延迟τ取1即可。 (2)引入排列熵的EEMD降噪方法。 将排列熵引入EEMD的目的,是根据排列熵判断异常信息的去除情况。该方法的具体操作步骤如下。 ①向含噪信号x(t)添加等长度均值为零、幅值标准差为常数的高斯白噪声ni(t)。 ②引入排列熵判断分解得到IMF的随机性大小,并设定阈值θ1;如果IMF分量的排列熵值大于阈值θ1,则认为IMF分量随机性较强,信号仍包含异常信息干扰,需要继续进行EEMD分解;如果小于阈值θ1,则认为IMF分量较规则,异常信息基本被去除,分解停止添加高斯白噪声,并将分解得到的前k个IMF分量从原始信号中分离,如式(9)所示: (9) ③对剩余信号r(t)进行EMD分解,完成IMF的全部分离。 ④计算所有分解分量与原始信号x(t)之间的相关系数,并设定阈值θ2;利用相关系数的大小,区分噪声分量与真实分量。 ⑤去除噪声分量,重构保留下来的真实分量,最终实现降噪。 为了测试方法的有效性,选择具有典型调频调幅特性的仿真信号进行验证,其表达式为: x(t)=(t2+1/10)cos(2π×8t2+π) (10) 仿真过程中,采样时间为1 s,采样间隔为0.000 5 s。 针对振动信号常混入噪声干扰和脉冲影响的实际情况,向仿真信号中添加标准差为0.3的高斯白噪声n(t)和幅值为1的正、负脉冲干扰s(t),组成含噪信号x′(t),其表达式如下: x′(t)=x(t)+n(t)+s(t) (11) 含噪信号x′(t)的时域波形及时频谱分析如图2所示。 图2 x′(t)时域波形及时频谱分析图 图2中,HHT为希尔伯特黄变换(Hibert-Huang transform)。从图2(a)能够清晰地观察到:在0.35 s、0.89 s处出现幅值为1的正脉冲干扰,在0.51 s处出现幅值为1的负脉冲干扰。 为了更好地对比本节提出的降噪方法的具体效果,分别应用小波降噪、EMD降噪、EEMD降噪以及改进的EEMD降噪方法,对含噪信号x′(t)进行降噪处理,并对以上方法的降噪效果进行对比分析。图3~图5分别对应小波降噪、EMD降噪、EEMD降噪的降噪结果以及对应信号时频谱。 图3 含噪信号小波降噪处理示意图 图4 含噪信号EMD处理示意图 图5 含噪信号EEMD处理示意图 比较图2(a)、图3(a)、图4(a)、图5(a)在信号0.35 s、0.51 s和0.89 s处正、负脉冲的分离效果可知,小波分解和EMD处理效果相对较差,EEMD处理效果有所改善,改进EEMD处理效果最优,进而证实了EEMD在处理模态混叠问题上的优势。 对比图2(b)、图3 (b)、图4(b)、图5(b)各种方法的降噪结果发现,小波降噪对高斯噪声和脉冲干扰起到一定的抑制作用,但以信号失真作为代价;EMD降噪在一定程度上能够有效地反映信号特征,但是由于端点效应以及模态混叠等方面的影响,导致EMD方法在处理脉冲干扰和还原边界信息方面效果不佳;传统EEMD降噪与本节提出改进EEMD降噪方法在整体处理效果上明显优于小波降噪和EMD降噪,不仅能够有效去除脉冲干扰、分离噪声成分,而且还能最大程度地保留信号原始特征,这可以通过降噪信号时频谱得到验证。相比于传统EEMD降噪,改进方法处理后得到的降噪信号更为平滑。 为了更好地说明不同方法之间的降噪效果,引入信噪比(signal noise ratio,SNR)作为定量对比指标。原始加噪、小波降噪、EMD降噪、EEMD降噪和改进EEMD降噪方法的SNR分别为8.251 4、18.619 2、21.741、30.104 8和35.379 2。 与传统方法相比,本文提出的方法降噪效果更明显,能够更加有效地去除噪声干扰。然而仅仅通过信噪比的对比,并不能有效反映改进方法在降噪过程中计算效率方面的提高。通过比较传统EEMD降噪和本节所提改进方法处理含噪信号过程的时间,验证了改进方法在降低运算耗时方面的突出表现。 传统EEMD降噪方法与本文方法的耗时对比如表1所示。 表1 耗时对比 表1表明,改进方法在很大程度上减少了EEMD迭代的次数,计算效率明显提高。 将排列熵引入EEMD降噪,可以对EEMD分解得到的IMF随机性进行检验。在EEMD分解过程中,高频分量和异常分量的随机性相对较大,相应排列熵值也较大,并且会被率先分解;低频分量分布规则随机性较小,多为平稳信号,对应排列熵较小,分解出现位置靠后。利用这种随机性大小的差异以及分解过程中对应高频到低频的次序关系,通过排列熵阈值的有效设置,能够有效地减小或避免不必要噪声的添加,从而提高了降噪效果和计算效率。 [1] 苑宇,李宝良,姚世选.基于吸引子SVD降噪的改进EMD方法[J].振动、测试与诊断,2010,30(3):325-329. [2] WU Z H,HUANG N E.Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009(1):1-41. [3] BANDT C,POMPE B.Permutation entropy: a natural complexity measure for time series[J].Physical Review Letters,American Physiological Society,2002,88(17):174102. [4] 安怀志.希尔伯特-黄变换理论和应用的研究[D].哈尔滨:哈尔滨工业大学,2008. [5] 任龙诗.EMD时频分析的理论与应用研究[D].哈尔滨:哈尔滨工业大学,2009. [6] 刘慧婷.EMD方法的研究与应用[D].合肥:安徽大学,2004. [7] 冯辅周,饶国强,司爱威,等.排列熵算法研究及其在振动信号突变检测中的应用[J].振动工程学报,2012,25(2):221-224. [8] 王余奎,李洪儒,叶鹏.基于多尺度排列熵的液压泵故障识别[J].中国机械工程,2015,26(4):518-523. [9] 程军圣,马兴伟,杨宇.基于排列熵和VPMCD的轴承故障诊断方法研究[J].振动与冲击,2014,33(11):119-123. [10]王磊,纪国宜.基于EMD模糊熵和SVM的转子系统故障诊断[J].噪声与振动控制,2012,26(3):171-176. An EMD De-noising Method for Vibration Signal and Its Simulation Analysis Aiming at the modal aliasing problem appears in emsemble empirical mode decomposition(EEMD) de-noising application,the method combing permutation entropy and empirical mode decomposition(EMD) is proposed to de-noise the vibration signal.The concept of permutation entropy is introduced and used in randomness test of intrinsic mode function(IMF) decomposed by EEMD,thus the new EEMD de-noising method is formed.The simulation results show that the method can effectively improve the signal-noise ratio; and greatly raise the operation efficiency. Empirical mode decomposition (EMD)Ensemble EMD (EEMD)Auxiliary noiseDe-noisingModal aliasingIntrinsic mode function(IMF)Permutation entropySimulation 李永军(1972—),男,2012年毕业于军械工程学院兵器发射理论与技术专业,获博士学位,副教授;主要从事结构损伤识别方向的研究。 TH-39;TP391 A 10.16086/j.cnki.issn 1000-0380.201609004 修改稿收到日期:2016-02-15。
3 仿真验证



4 结束语
