基于T-S模糊决策的PMSG风电系统广义预测控制

安爱民　杨国强　张浩琛　王　静　吕　斌　杨志强

(兰州理工大学电气工程与信息工程学院1，甘肃 兰州　730050;国网甘肃省电力公司经济技术研究院2，甘肃 兰州　730050;国网甘肃省电力公司兰州供电公司3，甘肃 兰州　730070;国网甘肃省电力公司电力科学研究院4，甘肃 兰州　730050;国网甘肃省电力公司武威供电公司5，甘肃 武威　733000)



基于T-S模糊决策的PMSG风电系统广义预测控制

安爱民1杨国强2张浩琛1王静3吕斌4杨志强5

(兰州理工大学电气工程与信息工程学院1，甘肃 兰州730050;国网甘肃省电力公司经济技术研究院2，甘肃 兰州730050;国网甘肃省电力公司兰州供电公司3，甘肃 兰州730070;国网甘肃省电力公司电力科学研究院4，甘肃 兰州730050;国网甘肃省电力公司武威供电公司5，甘肃 武威733000)

为提高风力发电系统在额定风速下的最大风能追踪性能，以永磁同步风力发电机(PMSG)为研究对象，采用局部等效建模方法，获得 PMSG 多工况运行的T-S模糊模型。以模糊规则后件作为受控自回归增量滑动平均(CARIMA)模型，采用广义预测控制(GPC)算法，对各模糊规则设计独立的GPC控制器，预测PMSG转速输出。仿真结果表明，在阶跃风速和组合风速的扰动下，基于T-S模糊决策的PMSG转速输出(如调节时间和超调量)较PI方法有明显下降，转速响应速度有大幅提高，最佳叶尖速比稳定在最优值，风能利用率显著提升。

风电系统永磁同步风力发电机T-S模糊模型控制器额定风速最大风能追踪广义预测控制风能利用率

0　引言

针对风力发电系统在额定风速以下的最大风能追踪问题，大多数文献给出的控制方法均是采用基于工作点线性化的经典线性控制策略进行控制器设计[1-5]。但这类控制器无法精准控制工作点以外的工况区间，难以应对风速变化的大范围和强频率问题。

Takagi-Sugeno(T-S)模糊模型是通过局部线性建模和加权组合实现全局线性化的方法，其本质依然是非线性系统[6]，在风力发电系统的建模和控制问题上具有独特的优势[7-8]。本文综合考虑风电系统的模型非线性特性和对控制性能的要求，提出通过局部建模推导出永磁同步风力发电机(permanent magnet synchronous wind power generator，PMSG)的T-S模糊模型。以T-S模糊模型后件部分作为预测模型，利用广义预测控制(generalized predictive control,GPC)算法预测发电机转速输出，形成PMSG风力发电机的T-S模糊广义预测控制算法(fuzzy generalized predictive control,FGPC)，并在阶跃风速和组合风速的扰动下进行仿真分析。

1　永磁同步风力发电机组建模

1.1风力机空气动力学

由贝茨理论可知，风力机获得的功率为：

(1)

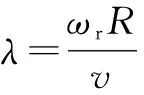
风力机输出转矩为：

(2)

风力矩系数CT(λ,β)的表达式为：

(3)

当风力机处于额定风速以下时，风力机将保持在最佳叶尖速比(λ=λopt)状态。此时，β=0，Cp(λ,β)达到最大，获得最大风能利用率。

风力矩系数又可表示为:CT(λ,β)={0.479-0.016 7β×sin[π(λ-3)/(15-0.3β)]-

0.001 8(λ-3)β}/λ

(4)

1.2PMSG系统动态模型

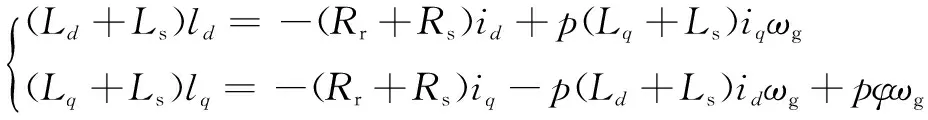
(5)

式中：Rr为定子电阻；p为极对数；Ld和Lq分别为定子d轴和q轴电感；id和iq分别为定子d轴和q轴电流；φ为永磁同步电机磁通。

发电机电磁转矩为：

Tg=p[φiq+(Ld-Lq)idiq]

(6)

2　PMSG 的T-S模糊模型

本节基于T-S模糊规则，通过动态方程建立PMSG的T-S模糊模型。

一般动态方程为：

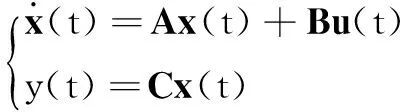
(7)

式中：x为状态向量；A为系统矩阵；B为输入矩阵。

为了将PMSG表示成上述形式，令式(7)中的x=[iqidωg]、控制输入u=Rs、控制输出y=wg,则有：

(8)

(9)

C=[100]T

(10)

则PMSG可以表示成式(7)。

根据T-S模糊模型的结构形式，定义前提变量z1(t)=id、z2(t)=iq、z3(t)=ωg，则PMSG的T-S模糊规则可以写为：

(11)

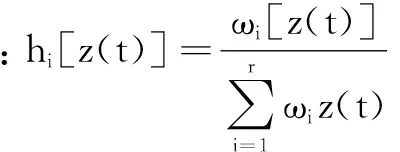
式(11)是PMSG通过T-S模糊方法线性化后，由加权组合得到的全局模型。

3　GPC 控制设计

3.1PMSG系统预测模型

广义预测作为一种先进控制方法，具有预测模型、滚动优化和反馈校正的基本特征，控制性能和鲁棒性[9-10]较好，被广泛用于工业过程控制。与传统控制方法相比，广义预测具有更加优越的控制性能。文献[11]～[13]将预测控制算法用于风力发电系统的控制过程，取得了不错的效果。

广义预测控制通常采用受控自回归增量滑动平均(controlled auto regressive incremental moving average,CARIMA)模型：

(12)式中：A(z-1)、B(z-1)和C(z-1)为后移算子z-1的多项式，一般取C(z-1)=1；u( )和y( )分别为被控对象的输入与输出；Δ=1-z-1为差分算子；ζ(k)为白噪声。

(13)

上文给出的式(11)表示整个PMSG动态系统，其包含多个模糊规则，每一条模糊规则后件参数均不相同，代表不同工况下的输入/输出关系，为线性时变模型。而每条规则的后件部分均是简单的线性函数，为线性时不变模型(linear time invariant,LTI)。本文以每条规则所决定的子线性模型作为预测模型，预测发电机的未来输出转速。

3.2滚动优化

广义预测控制(generalized predictive control,GPC)采用最小方差优化控制，其性能指标函数如下[14-15]:

(14)

式中：y(t+j)为y(t)的向前j步预测；Δu(t+j)=0,j=Nu,…,N1；N0和N1分别为最小和最大预测时域；Nu为控制时域；λ(j)为控制加权序列；ω(t+j)为输出参考值。

(15)

式中：α为柔化因子，0<α<1。

预测控制的目的是使下一时刻的输出尽可能地接近输出参考值ω(t+j)。

为了使用k时刻的输出数据以及过去和未来控制量的输入/输出数据，预测第(k+j)步的输出y(k+j)，引入丢潘图(Diophantine)方程：

1=Ej(z-1)A(z-1)+z-jFj(z-1)

(16)

为了获得第(k+j)步预测输出，丢潘图方程可以写为：

1=Ej(z-1)A(z-1)+z-(j+1)Fj(z-1)

(17)

丢潘图方程解为：

(18)

则预测输出为：

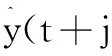
Gjp(z-1)Δu(t-1)+Hj(z-1)×

Δv(t+1)Hjp(z-1)Δv(t)

(19)

上式可以写为:

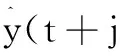
(20)

fj=Fj(z-1)y(t)+Gjp(z-1)Δu(t-1)+

Hj(z-1)Δv(t+j)+Hjp(z-1)Δv(t)

(21)

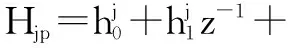
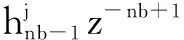
由∂J/∂Δu=0，可得最优控制率为：

Δu=(GTG+λI)-1GT[yr-Fy-HΔu(t-1)]

(22)

3.3FGPC预测控制

采用与式(12)相同的前提变量和模糊集合，则第i条子线性模型控制规则为:

thenui(k)=si[yr-HiΔu(k-1)-Fiy(k)]

基于并行分布补偿策略(parallel distributed compensation,PDC)，即每一条控制模糊规则的前件与相应模糊系统规则前件相同，全局控制率由各子规则的控制率通过各变量隶属函数加权求得，那么：

(23)

上式即为基于 T-S模糊决策的GPC全局状态方程。

4　仿真分析

本文以5 kW永磁同步风力发电机为研究对象，选取7个工况点建立T-S模糊规则，各前提变量分别如下：

id=[0.23,0.34,0.71,0.76,0.80,1.49,1.75]

iq=[5.25,6.37,7.41,8.58,9.26,10.71,11.82]

wg=[265,280,342,383,396,558,620]

选取三角形隶属函数，仿真参数如表1所示。

表1　仿真参数

设预测时域为5、控制时域为6、柔化系数为0.7，采用Matlab(R2008a)软件进行仿真。

FGPC预测转速与PMSG实际输出转速对比曲线如图1所示。

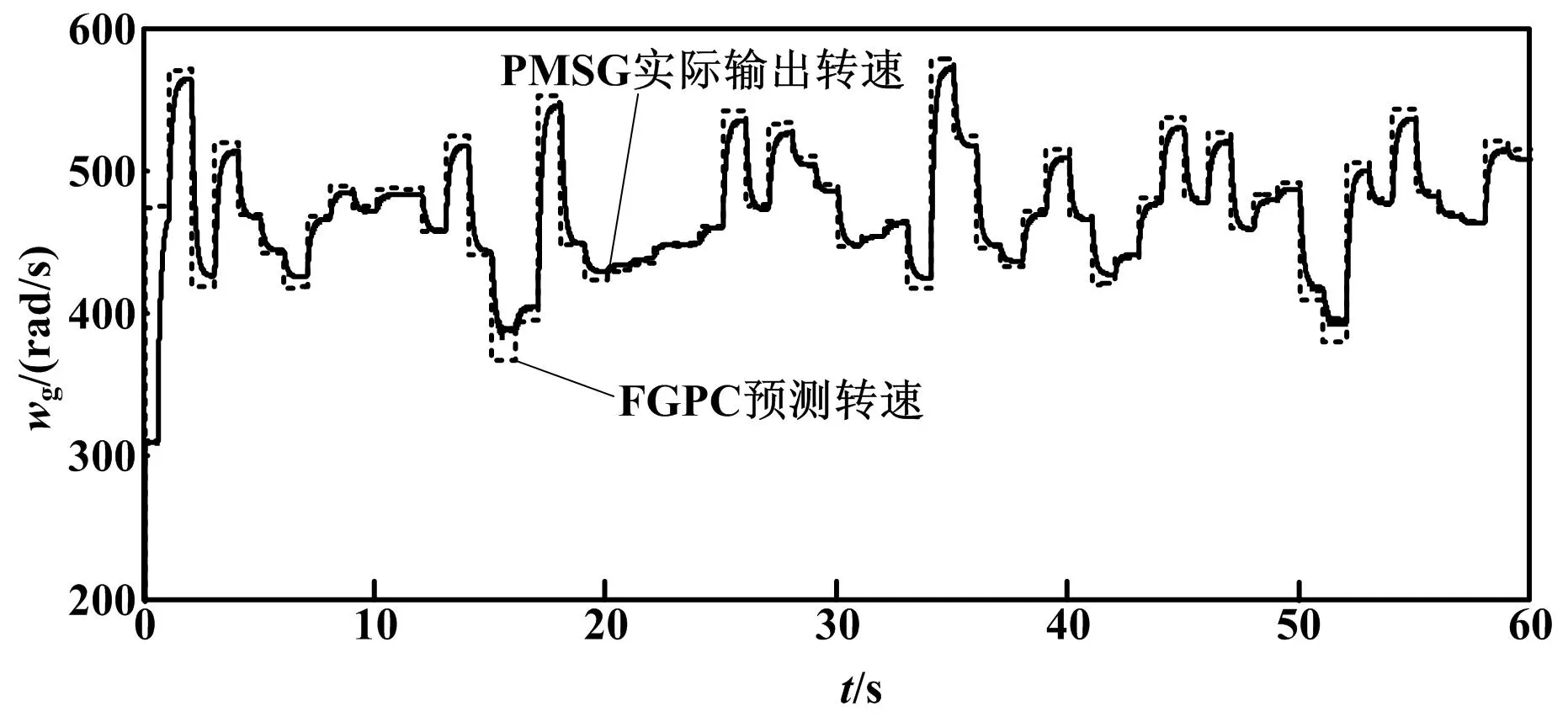
图1　转速对比曲线图

图1中，虚线表示FGPC预测转速，实线表示PMSG实际输出转速。由图1可以看出，实、虚曲线吻合度较高。通过计算可知，两者最大误差转速为19 rad/s，误差百分数为3.33%，说明FGPC预测精度良好。

PI和FGPC控制转速曲线如图2所示。

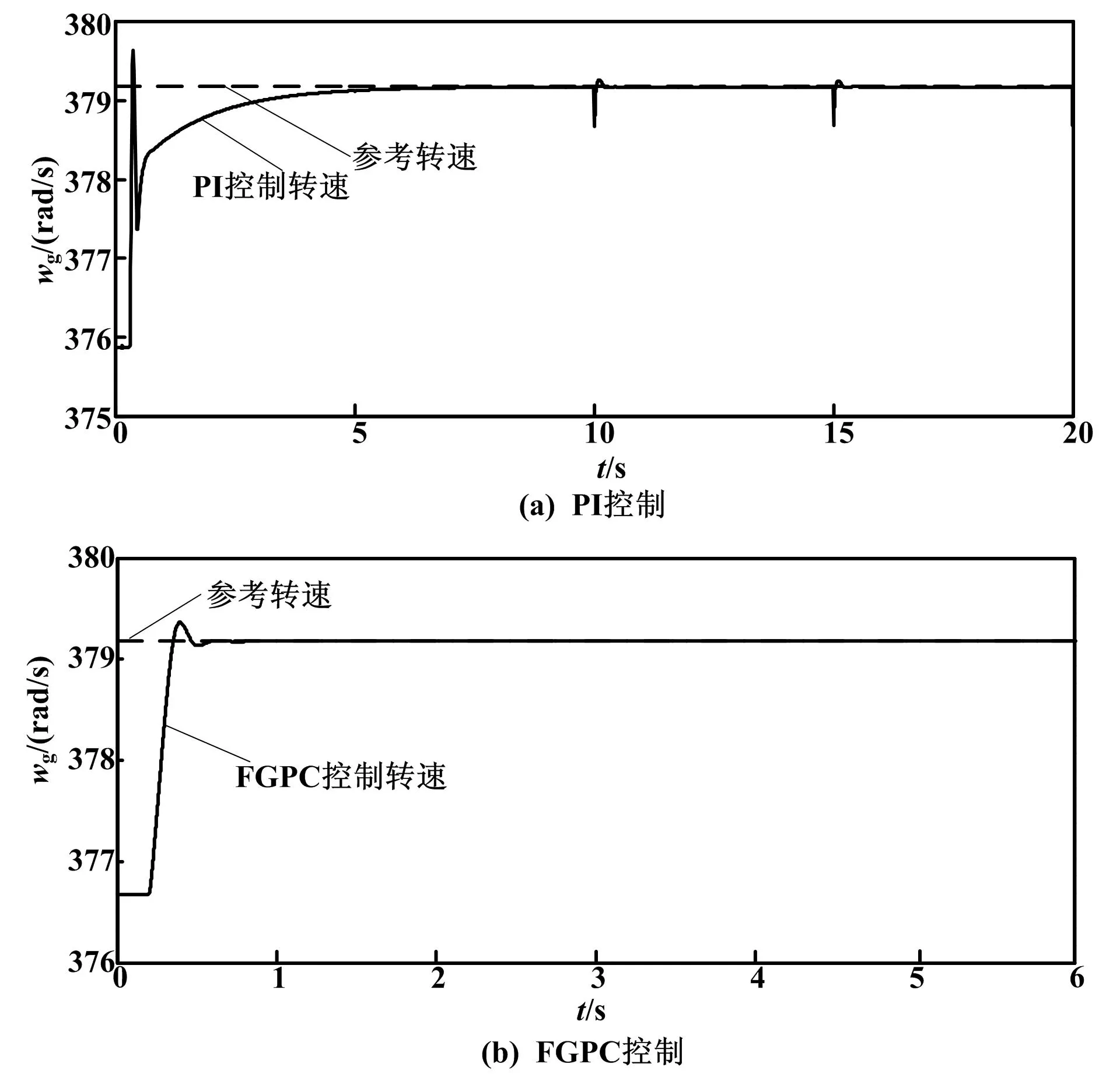
图2　PI和FGPC控制转速曲线

图2(a)为突加风速8 m/s扰动时，PI控制下的PMSG转速响应。PI控制器比例环节增益和积分环节增益分别为KP=1.818、KI=2.20。经计算，其超调为0.131 9%，震荡调节时间约为5.2 s，此刻达到转速稳态值379.2 rad/s，并保持不变。PI控制下，有部分超调量的调节时间过长，严重制约了PMSG快速跟踪风速变化的响应速度，而且在第10 s和15 s时，波形分别出现了毛刺，影响了转速输出质量。

图2(b)为突加风速8 m/s扰动时，FGPC控制下的PMSG转速响应，其超调量为0.026 4%，转速在0.65 s左右即可达到稳态值379.2 rad/s，并保持不变。和PI控制效果相比，超调效应和调节时间大大降低，有效地提高了转速输出质量。

图3为组合风速扰动下FGPC控制转速曲线，实线表示FGPC控制转速，虚线表示参考转速。组合风速模型由基本风、渐变风、阵风和随机风组合而成。基本风速为8.5 m/s，渐变风和阵风的最大风速值均为3 m/s，随机风由白噪声产生，采样时间为0.5 s。由图3可以看出，实际转速能够快速稳定地跟踪参考转速，跟踪性能比较理想。

图3　组合风速扰动下FGPC控制转速曲线

转速参考曲线可以由式(24) 和式(25)计算得到[15]：

(24)

(25)

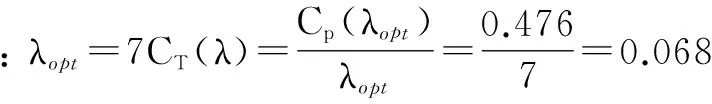
FGPC和PI两种控制方法下，PMSG风电机输出的叶尖速比曲线如图4所示。

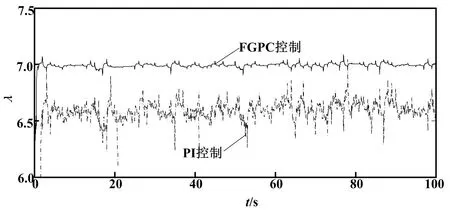
图4　叶尖速比曲线

由图4可以看出，FGPC控制下的叶尖速比输出更加稳定，更接近最佳叶尖速比，叶尖速比能够稳定在最优值7的位置。

5　结束语

利用T-S模糊推导法建立风力PMSG的T-S模糊模型，并以此模型作为预测模型，采用GPC算法，通过模糊决策形成全局控制器，对发电机进行转速追踪控制。仿真结果表明，T-S模糊模型具有很高的逼近精度，能准确地反映系统的动态行为。基于FGPC的PMSG风电系统具有很好的动态性能，能快速跟踪风速变化，将叶尖速比稳定在最佳值7，明显优于PI控制，有效实现了风能最大追踪利用。

[1]GUPTARA,SINGHB,JAINBB.WindenergyconversionsystemusingPMSG[C]//2015InternationalConferenceonRecentDevelopmentsinControl,AutomationandPowerEngineering,2015: 199-203.

[2]MAGRIE，GIRIF，ELFADILIA，etal.WindsensorlesscontrolofwindenergyconversionsystemwithPMSgenerator[C]//AmericanControlConference，Montreal，IEEE，2012:2238-2243.

[3]NGUYENHM，NAIDUDS，MOUSAVINEZHADSH.H∞optimalfilteringandcontrolofwindenergyconversionsystems[C]//IEEEInternationalConferenceonElectro-InformationTechnology， 2013:1-6.

[4]WUDH,LIYY,JIZC,etal.Self-adaptivePIDoptimalcontrolofwindenergyconversionsystem[C]//The26thChineseControlandDecisionConference,2014: 13-17.

[5]VINODA，SINHAAK.Astudyonintelligentalgorithmsformaximumpowerpointtrackinginfieldofwindenergyconversionsystem[C]//2014InternationalConferenceonElectronicsandCommunicationSystems，2014:1-4.

[6]TAKAGIT，SUGENOM.Fuzzyidentificationofsystemsanditsapplicationstomodelingandcontrol[C]//TransactionsonSystems，ManandCybernetics，1985，15(1):116-132

[7]OUYANGYL，LIANK.SensorlessT-Sfuzzycontrollerforwindpowergeneratingsystems[C]//SICEAnnualConference2010，ProceedingsofIEEE，2010:3395-3400.

[8]OUYESSAADH，CHAFOUKH，LEFEBVRED.FaultsensordiagnosiswithTakagi-SugenoapproachdesignappliedforDFIGwindenergysystems[C]// 3rdInternationalConferenceonSystemsandControl，2013:55-60.

[9] 王利兵，毛承雄，陆继明，等. 基于反馈线性化原理的直驱风力发电机组控制系统设计[J]. 电工技术学报，2011，26(7):1-6.

[10]胡耀华，贾欣乐. 广义预测控制综述[J].信息与控制，2000，29(3):248-256.

[11]ZHANGJH,WANGH,HOUGL,etal.Generalizedpredictivecontrolforwindturbinesystems[C]// 2010the5thIEEEConferenceonIndustrialElectronicsandApplications,IEEE,2010: 679-683.

[12]DIASSV，ASSUNCAODASILVAW，DOSREISLN，etal.RobustgeneralizedpredictivecontrolappliedtotherotorsideconverterofawindpowergeneratorsystembasedonDFIG[C]//2014 11thIEEE/IASInternationalConferenceonIndustryApplications，2014:1-6.

[13]BOUOUDENS，CHADLIM，FILALIS，etal.Fuzzymodelbasedmultivariablepredictivecontrolofavariablespeedwindturbine:LMIapproach[J].RenewableEnergy，2012，37(1):434-439.

[14]庞中华,崔红.系统辨识与自适应控制MATLAB仿真[M].北京：北京航空航天大学出版社,2009.

[15]ANA,YANGGQ,ZHANGHC,etal.T-SfuzzycontrolforPMSGmaximumwindpowerstabletracking[C]//The27thChineseControlandDecisionConference,2015:2844-2849.

Generalized Predictive Control Based on T-S Fuzzy Decision for PMSG Wind Power System

In order to improve and enhance the tracking performance for the maximum wind energy under the rated wind speed in wind power generation system,with the permanent magnet synchronous wind power generator (PMSG) as the research object,by the method of local equivalent modeling,the T-S fuzzy model of PMSG working under multiple operating conditions is obtained.Considering the consequent of fuzzy rules as CARIMA prediction model,generalized predictive control algorithm is used to design the independent GPC controller of each fuzzy rule,to forecast output of rotating speed of PMSG.The results of simulation show that under step wind speed or combined wind speed disturbance,comparing with PI method,the regulation time and overshoot of the output of rotating speed of the T-S fuzzy decision based PMSG are obviously decreased,while the response speed is greatly increased; the optimal tip speed ratio is stabilized around the optimum value,and the utilization of wind energy is enhanced.

Wind power systemPermanent magnet synchronous wind power generator(PMSG)Takagi-Sugeno(T-S) fuzzy modelControllerRated wind velocityMaximum wind energy trackingGeneralized predictive control(GPC)Utilization of wind energy

安爱民(1972—)，男，2010年毕业于兰州理工大学控制理论与控制工程专业，获博士学位，教授；主要从事新能源发电控制系统的研究。

TH7;TP27

A

10.16086/j.cnki.issn 1000-0380.201609001

国家自然科学基金资助项目(编号：61563032)；

甘肃省自然科学基金资助项目(编号：145RJZ024)。

修改稿收到日期：2016-01-16。