基于弹性地基板理论的桩网复合地基桩土应力比及沉降计算
2016-10-12赵明华刘猛马缤辉龙军
赵明华,刘猛,马缤辉,龙军
基于弹性地基板理论的桩网复合地基桩土应力比及沉降计算
赵明华1,刘猛1,马缤辉2,龙军1
(1. 湖南大学土木工程学院,湖南长沙,410082;2. 湖南科技大学土木工程学院,湖南湘潭,411201)
将桩网复合地基中的水平加筋垫层视为弹性薄板,垫层下的竖向桩体及桩间土体视为不同刚度的弹簧体系,基于Filonenko−Borodich双参数弹性地基模型,考虑加筋垫层的抗弯、拉作用,根据静力平衡建立薄板挠曲变形控制微分方程,并利用Bessel复变函数推导出相应的挠度函数。在此基础上,考虑桩土变形协调,推导桩网复合地基桩土应力比及沉降的计算公式。为验证本文方法的可行性,对某工程算例进行计算分析。最后,基于本文方法,探讨分析加筋垫层复合弹性模量、筋材拉力、桩土刚度比等因素对桩网复合地基桩土应力比和沉降的影响。研究结果表明:计算与实测结果吻合良好。桩土应力比随桩土刚度比、加筋垫层复合弹性模量及格栅拉力的增大而增大。
桩网复合地基;圆形薄板;双参数地基模型;桩土应力比;沉降
近年来,随着我国高速公路、铁路建设的兴起,软土地基问题日益突出,地基承载力不足、沉降过大、不均匀沉降等问题尤为严重。桩网复合地基作为由竖向桩体和水平加筋体构成的新型软基处理形式,对上述地基问题的处置具有良好的效果,且该地基处理方法施工简单、进度较快,在铁路软基处理中得到广泛的应用[1]。关于桩网复合地基的工作机理的研究,目前已取得了不少成果[2−4],其中桩土应力比与沉降作为反映桩网复合地基工作性状的重要参数,其计算方法的研究也一直是该领域的热点。其中,杨宇[5]利用螺旋线模拟垫层变形形状,考虑了垫层的“网兜效应”;陈昌富等[6]考虑加筋垫层抗拉作用,假设垫层变形后形状为旋转抛物面,基于Winkler地基推导了桩土应力比计算式;ABUSHARAR等[7]假设桩间土应力均布,利用垫层变形的圆弧假定,提出了一种桩土应力比的简易计算方法。对于相当一部分工程,单层格栅并不能满足工程需要,垫层中需设置土工格室或多层格栅,同时,HAN等[2]指出此类结构不同于单层格栅的情况,加筋材料与所包含的散体填料可形成一“柔性筏板”,具有较强抗弯作用,显然,上述基于薄膜理论所导出的方法因不能考虑抗弯作用并不适合于土工格室或多层格栅的情况。因此,饶为国等[8]为考虑“柔性筏板效应”将加筋垫层假设为薄板,假定薄板变形后形状为抛物线,推导了桩土应力比计算式;郑俊杰[9]则认为此类垫层不仅具有“柔性筏板效应”,同时也具有“拉膜效应”,于是假定加筋垫层变形为重三角函数形式,并考虑其变形过程中的几何非线性,从而获得了兼顾垫层“柔性筏板效应”与“拉膜效应”的桩土应力比及沉降计算方法。此外,由上述文献可知,加筋体变形形状是计算桩土应力比以及沉降的前提和关键,不同的变形形状所求得的桩土应力比与沉降也不相同,所以越接近于加筋垫层实际变形所求得的桩土应力比与沉降也就越准确,而上述文献均事先假定了加筋体的变形,不能真实反映加筋体的受力状态,这导致计算结果与实测结果的误差较大。为此,谭慧明等[10]基于Winkler弹性地基矩形板理论推导出了三维情况下水平加筋体的挠曲函数,但受限于矩形板边界条件的复杂性,难以考虑桩体沉降对于加筋垫层的影响;之后,赵明华等[11−12]以单桩影响范围内复合地基为研究对象,将桩土分别离散成不同刚度的弹簧系列,借助于弹性地基圆板理论与桩土界面处垫层的变形协调,导出了考虑桩土共同变形的加筋垫层的挠曲函数,在此基础上提出了桩土应力比的计算方法。而上述2种分析方法,依然只考虑了加筋垫层的“柔性筏板作用”,并未考虑筋材的“拉膜效应”。由上述分析可知:在未假定加筋垫层变形情况下,综合考虑垫层的“柔性筏板效应”、“网兜效应”与桩土共同变形,是准确求解桩网复合地基桩土应力比及沉降的关键,为此,本文作者基于Filonenko−Borodich双参数地基模型,综合考虑加筋垫层的“柔性筏板效应”与“网兜效应”,同时考虑桩土变形,根据Bessel复变函数推导出加筋垫层的挠曲变形的解析函数,进而得出桩网复合地基桩土应力比和沉降的计算表达式,以期进一步完善桩网复合地基桩土应力比与沉降的计算方法。
1 计算模型及基本假设
取如图1所示的单桩影响范围内的典型单元体进行分析,桩体直径为,中心距为d,单桩加固范围直径为e,正方形布桩时,e=1.13d,梅花形布桩时,e=1.05d。

图1 桩网复合地基示意图
为进一步简化计算进行如下假定。
1) 桩网复合地基计算模型如图2所示,将单桩加固范围内的加筋垫层视为置于Filonenko−Borodich双参数地基模型[13]上的弹性圆薄板,其中筋材拉力可用下式求得:
其中:g为筋材平均应变;g为加筋体的抗拉刚度。
2) 桩体对薄板的竖向支撑力p为均布力,根据文献[6],[10]及[11],桩与桩间土变形均符合Winkler地基模型;
3) 不考虑差异沉降所引起的路堤荷载重分布的情况,即路堤荷载为均布荷载[7−8, 11]。
2 桩顶加筋体变形分析
令1()表示桩顶加筋体的挠曲函数,根据Filonenko−Borodich双参数地基模型,在路堤荷载与桩顶反力p共同作用下,桩顶加筋体的控制微分方程为
式(2)所对应的齐次方程通解为
式中:J,Y分别为第一类和第二类阶Bessel函数;1,2,3和4为待定常数。
均布荷载及支持力p作用下,式(2)的特解为,结合式(4),因此桩顶薄板挠曲变形函数为

3 桩间土顶部薄板变形分析
令2()表示桩顶薄板的挠曲函数,在均布荷载与地基土支撑作用下,桩间土顶部薄板的控制微分方程为
式中:s为桩间土基床系数。
为简化计算,令
式(6)所对应的齐次方程可转化为如下形式:
由式(7)可知:21与22根据2−4s的正负分为实数与虚数2种情况,而2种情况下方程(8)的解不同。下面就这2种情况进行讨论。
1) 当2≥4s时,令
式(8)的通解为
式中:N为第二类阶虚变量Bessel函数;5,6,7和8为待定常数。
均布荷载作用下,式(6)的特解为2*=/s,结合式(10),可得2≥4s时,桩间土顶部薄板挠曲变形函数:
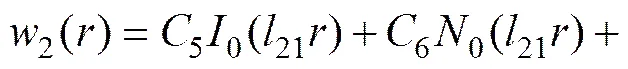
(11)
2) 当2<4s时,式(6)的通解可构造[13]为
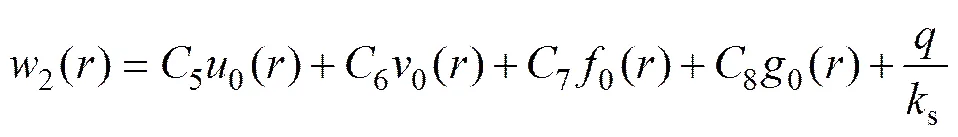
式中:u和v分别为阶第一类Bessel函数的实数部分与Hankel函数的实数部分;f和g分别为阶Bessel函数的虚数部分与Hankel函数的虚数部分。
4 待定系数求解
要最终确定薄板的挠曲函数,还要对式(5),(11)和(12)中的未知参数1,2,…,8及p通过边界及连续条件进行求解。
由于圆板中心处(=0)的薄板转角为0,可得2=3=0。
在桩土交界处,薄板挠度、转角、径向弯矩以及剪力的连续条件如下:
此外,根据假设(2),桩土交界处圆板的挠度1(/2)为
桩顶反力p为上部路堤荷载与垫层向桩体转移荷载之和,即
根据文献[2],单元体=e/2处转角与剪力边界条件如下:
同时,根据薄板挠曲函数式(5),(11)及(12),可得薄板转角、径向弯矩、剪力表达式如下。
1) 在桩顶范围内,即0≤≤/2时,
2) 在桩间土范围内,即e/2≤≤/2时,分2种情况考虑。
①当2≥4s时,
②当2≥4s时,为简化表达,令,,根据欧拉公式可得
结合式(20),可得
(21)
式中:Z()(其中=1,2,3,4)分别表示u(),v(),f(),g()。
根据上述分析,联立方程(14)~(17)可求出1,4,…,8及p,从而得到板的挠度表达式。
5 桩土应力比及沉降计算
由上述分析可知:如计算前已知筋材应变,可直接利用式(1)计算筋材拉力,进行待定系数求解。然而,多数工程中并未事先对筋材变形进行测量,针对此类情况,曹新文等[4]通过现场试验研究发现,路堤荷载下筋材平均应变与沉降近似成如下关系:
式中:和为相关拟合参数,可根据沉降计算位置,按文献[4]中所列表格选取,试验中所采用的格栅抗拉刚度为50 kN/m。
根据上述研究成果,选取加筋体最大挠度2(e/2)作为式(22)中沉降,筋材拉力未知情况下,待定系数的求解步骤如下:
1) 假定初始拉力0(0可以取很小的值),将其代入式(2)与式(6)中求解加筋垫层的挠曲函数,得到1(/2)与2(e/2);
2) 将前一次得到2(e/2)作为,代入式(22),并结合式(1)求得拉力,而后重新将代入式(2)与式(6),求解加筋垫层的挠曲函数,得到1(/2)与2(e/2);
3) 选定误差,将所得到1(/2)和2(e/2)并与前一次的结果进行比较,若比较结果均小于误差,则停止计算,否则继续按照步骤2)和3)进行迭代计算。
上述步骤流程如图3所示。
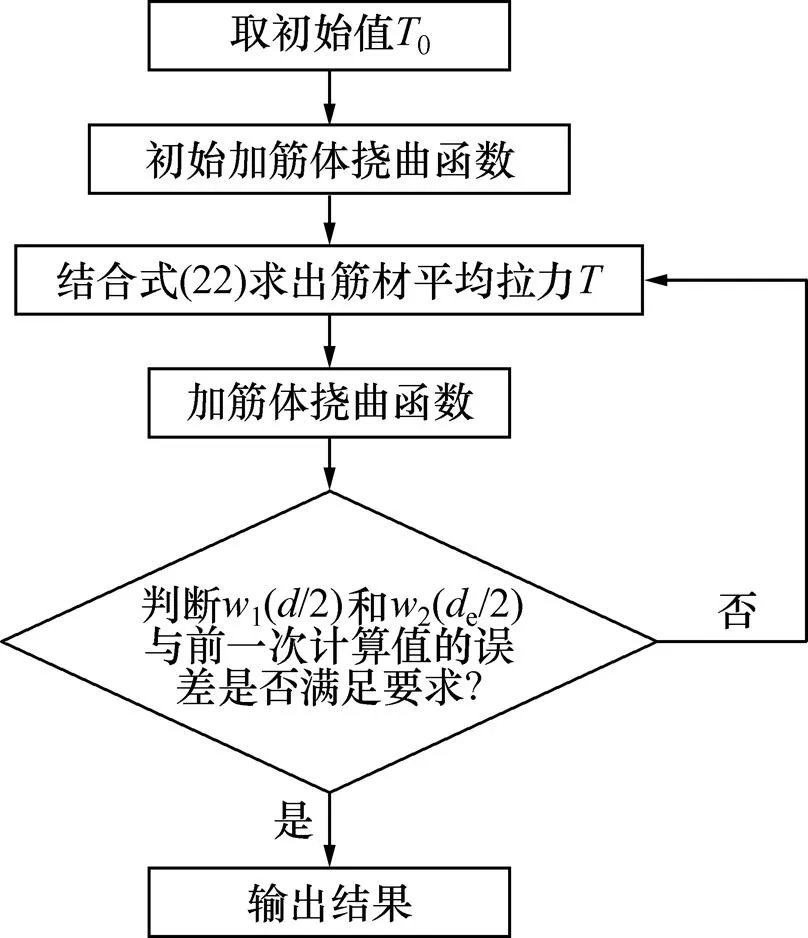
图3 计算流程示意图
得到加筋垫层的挠曲函数以及p后,由图2所示的计算模型可见,根据方向受力平衡,可得桩间土顶部平均竖向应力s为
则桩土应力比可按下式计算[14]:
文献[8]认为:在大面积堆载情况下,桩顶沉降较小,可将桩间土沉降作为地基沉降,则
6 相关参数确定方法
6.1 桩体变形刚度p
为综合考虑桩体变形过程中的非线性,桩体变形刚度取桩基载荷试验−曲线上割线斜率。
6.2 桩间土基床系数s
同样为综合考虑桩间土体变形过程中的非线性,桩间土基床系数s取载荷试验−曲线上割线斜率,如无实测资料,也可遵照地区经验取值,或按照下式确定:
式中:s为土体变形模量,多层土体按深度加权平均;s为土层厚度。
6.3 垫层计算厚度
从加筋材料与散体材料桩共同作用的角度出发,取加筋材料及其所包裹的填料所形成的复合结构的厚度,若为多层格栅,即为顶层与底层格栅之间的距离作为薄板厚度;若为土工格室,则可直接取土工格室的厚度。
6.4 垫层复合弹性模量
对于格栅垫层,郑俊杰等[9]给出了其复合弹性模量的确定方法,即取格栅弹性模量与垫层填料的变形模量的加权平均值;对于土工格室,杨明辉等[15]通过叠梁试验给出了不同型号土工格室配合各种常用填料所构成的多种格室垫层的平均弹性模量。
7 算例及参数分析
7.1 算例1
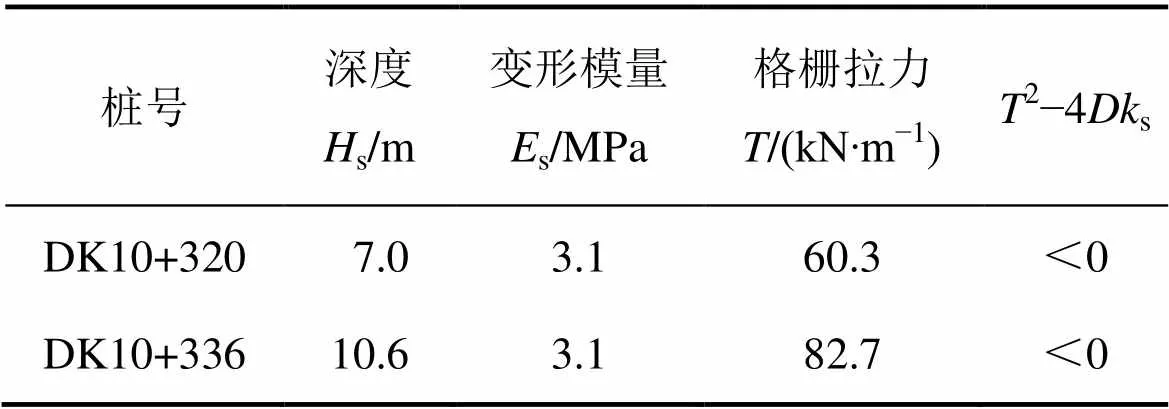
遂渝铁路DK10+320和DK10+336试验路段软土地基按桩网复合地基技术处理[4],桩体为粉喷桩,直径=0.50 m,桩中心距d=1.0 m,梅花形布桩e= 1.05 m,粉喷桩桩顶铺设双层双向抗拉刚度为50 kN/m的土工格栅,间距为30 cm。地基为第四纪洪积松软土,基岩为泥岩,上部填土荷载重度s=20 kN/m3,路基填筑高度=10m,碎石垫层c=25 kN/m3。根据静载试验,桩体变形刚度系数为p为2 000 kN/m。薄板厚度取0.3 m,复合弹性模量为52 MPa,泊松比为0.3,其他计算参数如表1所示。
表1 试验路段软土地基部分计算参数
Table 1 Partial calculation parameters for soft foundation
路堤中心沉降及土工格栅加筋垫层下方桩土应力比的计算值与实测值的比较见表2。
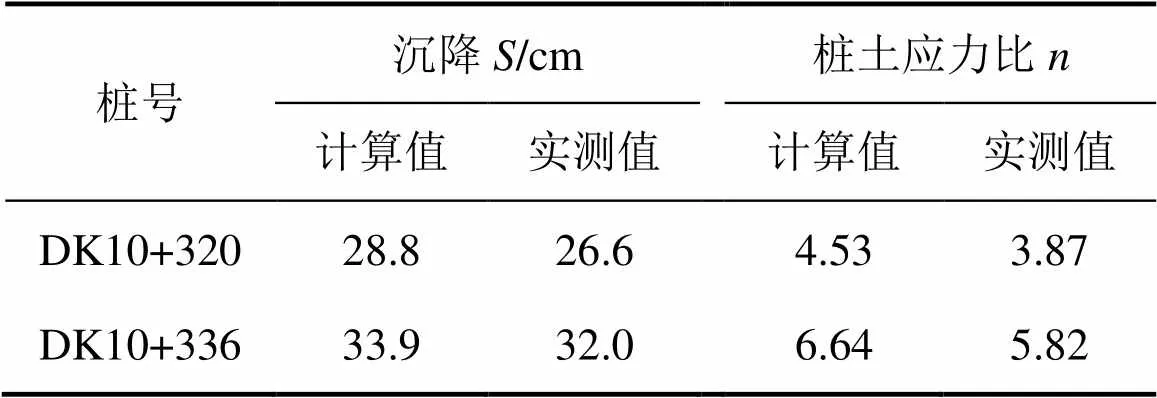
表2 算例1沉降与桩土应力比计算结果
DK10+336试验段地基沉降随路堤填土高度的变化如图4所示。由表2及图4可见:本文方法得出的双层土工格栅桩网复合地基桩土应力比及沉降均与实测值较接近。
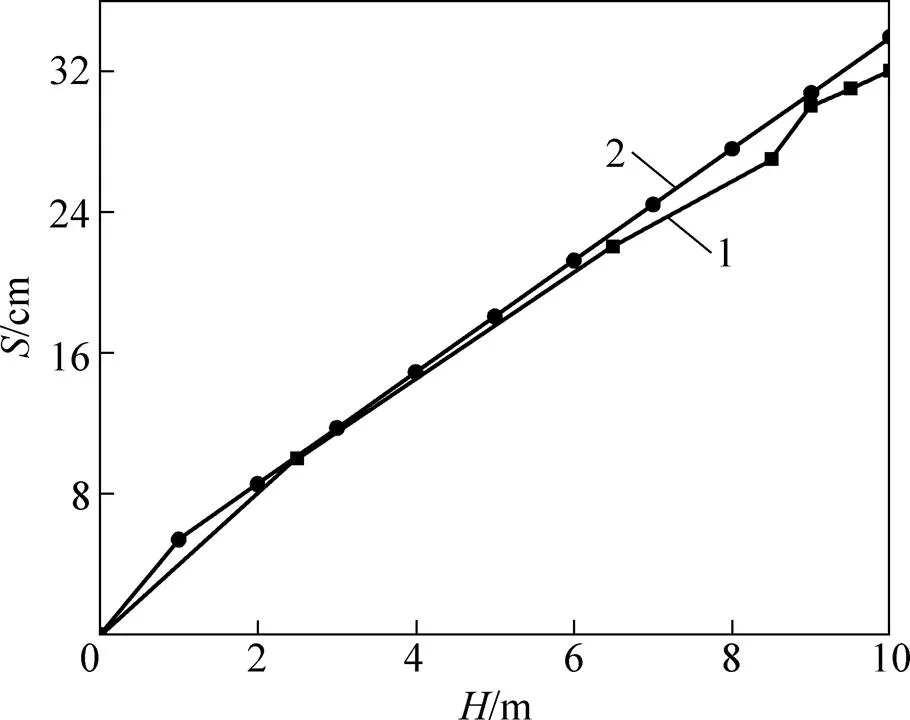
1—实测值;2—计算值。
7.2 算例2
湖南某高速公路软土地基试验路段采用土工格室+搅拌桩复合地基进行处理,搅拌桩直径为0.50 m,桩间距d=1.2 m,梅花形布桩,桩顶填筑1层厚30 cm砂垫层,中心设置1层厚度为10 cm的土工格室。地基为淤泥质黏土,上部填土荷载重度s= 20 kN/m3,试验路段路基填筑高度4 m。实测沉降为5.3 cm,桩土应力比为。桩体变形刚度系数p为2 355 kN/m,处理后桩间土基床系数s为1 024 kN/m3,薄板厚度为0.10 m,复合弹性模量为40 MPa,复合泊松比取0.3。
经计算桩土应力比与沉降如表3所示。
表3 算例2沉降与桩土应力比计算结果
Table 3 Results of settlement and pile-soil stress ratio for example 2

由表3可知:本文计算所得桩土应力比较文献[11]方法更为接近实测值,此外,沉降与实测值也较为接近。这是由于本文较文献[11]方法,考虑了格室体的抗拉作用。
7.3 参数分析
为进一步探讨分析加筋垫层复合弹性模量、格栅拉力、桩土刚度比等对桩网复合地基沉降及桩土应力比的影响,以算例2中参数为基础,针对上述因素进行相应的参数分析。
7.3.1 桩土刚度比对沉降及桩土应力比的影响
不考虑筋材拉力的影响,引入p=4p/(π2),表征桩体变形刚度及置换率的综合影响,其他参数不变。
沉降与桩土刚度比的关系如图5所示。可见:桩土刚度比对沉降的影响随着弹性模量的增大而增大。而且同一弹性模量时,复合地基的沉降随桩土刚度比增大而减小。但当桩土刚度比超过一定值时,继续增大桩土刚度比,对沉降的减小作用不大。

E/MPa:1—40;2—80;3—120;4—160。
桩土应力比与桩土刚度比的关系如图6所示。由图6可见:不同弹性模量时,桩土刚度比与桩土应力比两者关系呈非线性,且弹性模量越小,非线性现象越明显。此外,弹性模量越大,桩土刚度比对桩土应力比影响就越明显。
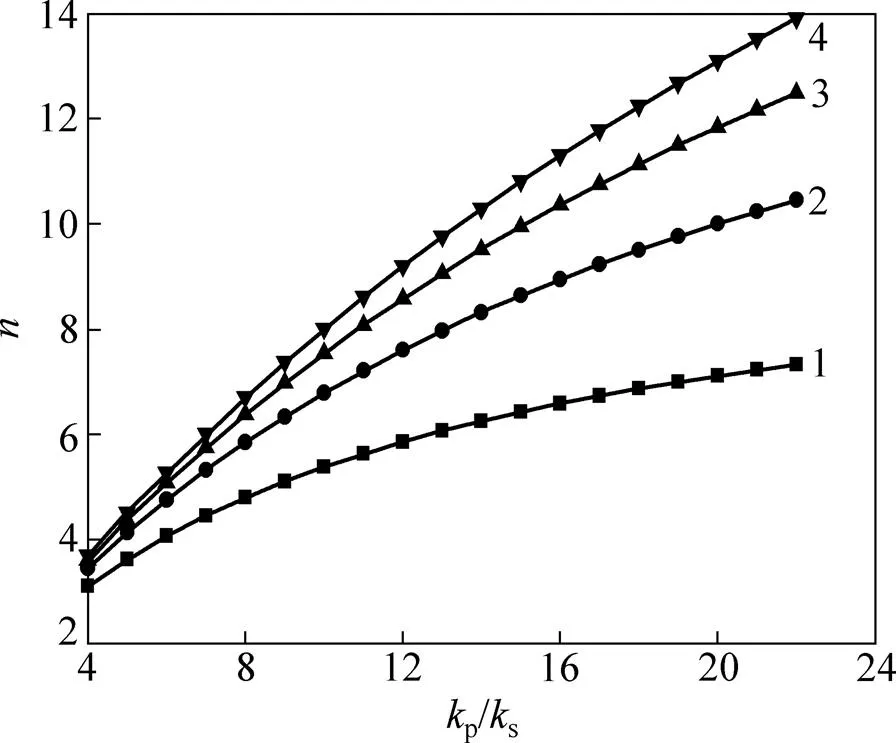
E/MPa:1—40;2—80;3—120;4—160。
7.3.2 筋材拉力对沉降及桩土应力比的影响
沉降和桩土应力比与筋材拉力的关系分别如图7和图8所示。由图7和8可见:对于同一弹性模量,沉降随筋材拉力增大而减小,而桩土应力比随拉力增大而增大。此外,对两者的影响随的增大而逐渐减弱。由此可见,当垫层材料的弹性模量较小时,采用级配材料,适当增大界面摩阻力可有效增大桩土应力比,减小沉降。
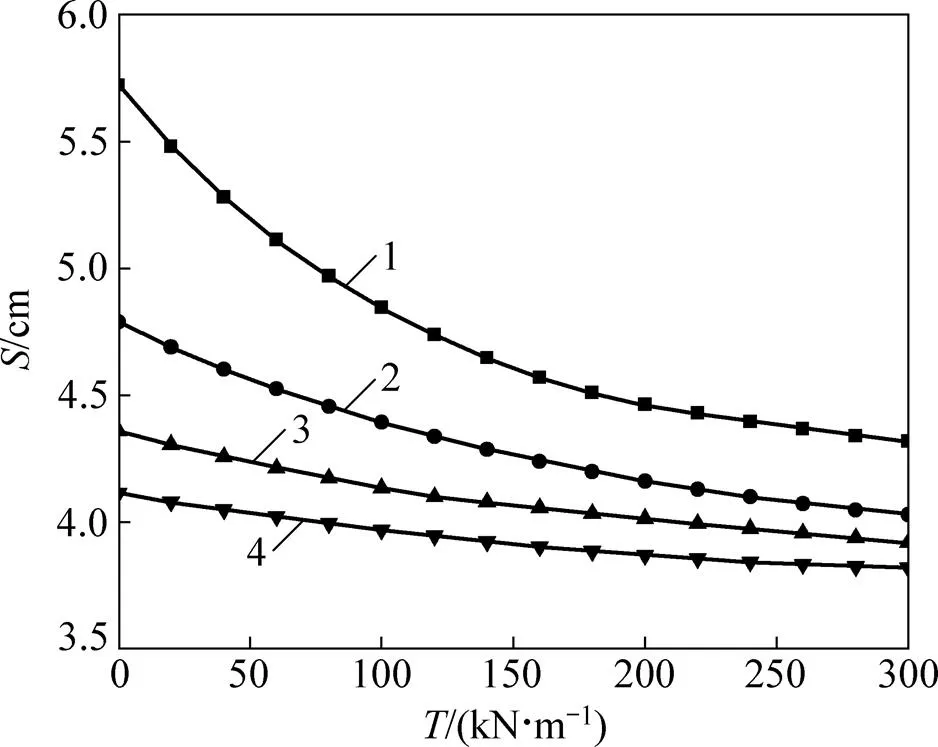
E/MPa:1—40;2—80;3—120;4—160。

E/MPa:1—40;2—80;3—120;4—160。
8 结论
1) 桩网复合地基沉降随桩土刚度比、格栅拉力及加筋垫层复合弹性模量的增大而减小。桩网复合地基桩土应力比随桩土刚度比、加筋垫层复合弹性模量及格栅拉力的增大而增大。当加筋垫层抗弯刚度较小时,筋材抗拉作用对桩土应力比、沉降的影响不能忽略。
2) 准确测定垫层复合弹性模量、格栅应变以及桩、土变形刚度是采用本文方法计算的关键。
[1] 王炳龙. 高速铁路路基工程[M]. 北京: 中国铁道出版社, 2007: 1−5. WANG Binglong. Sub grade engineering of high speed railway[M]. Beijing: China Railway Press, 2007: 1−5.
[2] HAN J, GABR M A. Numerical analysis of geosynthetic- reinforced and pile supported earth platforms over soft soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE 2002, 128(1): 44−55.
[3] ABDULLAH C H, EDIL T B. Behaviour of geogrid-reinforced load transfer platforms for embankment on rammed aggregate piers[J]. Geosynthetics International 2007, 14(3): 141−153.
[4] 曹新文, 卿三惠, 周立新. 桩网复合地基土工格栅加筋效应试验研究[J]. 岩石力学与工程学报, 2006, 25(Suppl 1): 3162−3167. CAO Xinwen, QING Sanhui, ZHOU Lixin. Experimental study on reinforcement effect of geogrid on composite foundation with dry jet mixing piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl 1): 3162−3167.
[5] 杨宇. 双向增强体复合地基承载特性研究[D]. 长沙: 湖南大学土木工程学院, 2006: 74−77. YANG Yu. Research on work mechanism of double direction reinforced composite foundation[D]. Changsha: Hunan University. School of Civil Engineering, 2006: 74−77.
[6] 陈昌富, 周志军. 双向增强体复合地基桩土应力比计算分析[J]. 岩土力学, 2009, 30(9): 2660−2666. CHEN Changfu, ZHOU Zhijun. Analysis of pile-soil stress ratio for double reinforced composite ground[J]. Rock and Soil Mechanics, 2009, 30(9): 2660−2666.
[7] ABUSHARAR S W, ZHENG Junjie, CHEN Baoguo, et al. A simplified method for analysis of a piled embankment reinforced with geosythetics[J]. Geotextiles and Geomemberanes, 2009, 27: 39−52.
[8] 饶为国, 赵成刚. 桩−网复合地基应力比分析与计算[J]. 土木工程学报, 2002, 35(2): 74−80. RAO Weiguo, ZHAO Chenggang. The behavior of pile-soil composite foundation[J]. China Civil Engineering Journal, 2002, 35(2): 74−80.
[9] 郑俊杰, 张军, 马强, 等. 双向增强体复合地基桩土应力比三维分析[J]. 华中科技大学学报(自然科学版), 2010, 38(2): 83−86. ZHENG Junjie, ZHANG Jun, MA Qiang, et al. Three dementional analysis of pile-earth ratio of biaxial reinforcement composite foundation[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2010, 38(2): 83−86.
[10] 谭慧明, 刘汉龙. 桩承式加筋路堤中路堤与褥垫层共同作用理论分析[J]. 岩土力学, 2008, 29(8): 2271−2276. TAN Huiming, LIU Hanlong. Theoretical analysis of cushion and embankment fills in pile-supported embankment[J]. Rock and Soil Mechanics, 2008, 29(8): 2271−2276.
[11] 赵明华, 刘敦平, 张玲. 双向增强体复合地基桩土应力比计算[J]. 工程力学, 2009, 26(2): 176−181. ZHAO Minghua, LIU Dunping, ZHANG Ling. Calculation for pile-soil stress ratio of two-direction reinforced composite foundation[J]. Engineering Mechanics, 2009, 26(2): 176−181.
[12] 赵明华, 刘猛, 龙军, 等. 双向增强体复合地基土工格室加筋体变形分析[J]. 中国公路学报, 2014, 27(5): 97−104. ZHAO Minghua, LIU Meng, LONG Jun, et al. Deformation calculation of geocell-reinforcement in bidirectional reinforced composite foundation[J]. China Journal of Highway and Transport, 2014, 27(5): 97−104.
[13] SELVADURAI A P S. 土与基础相互作用的弹性分析[M]. 范文田, 译. 北京: 中国铁道出版社, 1984: 157−163.SELVADURAI A P S. Elastic analysis of soil-foundation interaction[M]. FAN Wentian, trans. Beijing: China Railway Press, 1984: 157−163.
[14] 龚晓楠. 复合地基理论及工程应用[M]. 北京: 中国建筑工业出版社, 2002: 19−55.GONG Xiaonan. Theory and application of composite foundation[M]. Beijing: China Architecture and Building Press, 2002: 19−55.
[15] 杨明辉, 邓岳宝, 赵明华. 基于叠梁试验的土工格室垫层刚度确定方法研究[J]. 土木工程学报, 2011, 44(11): 87−92. YANG Minghui, DENG Yuebao, ZHAO Minghua. Study of stiffness test method of geocell cushion based on the superposed beam theory[J]. China Civil Engineering Journal, 2011, 44(11): 87−92.
(编辑 赵俊)
Calculation of pile-soil stress ratio and settlement of pile-net composite foundation based on elastic foundation plate
ZHAO Minghua1, LIU Meng1, MA Binhui2, LONG Jun1
(1. College of Civil Engineering, Hunan University, Changsha 410082, China;2. College of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)
The horizontal reinforced mattress was regarded as a thin plate based on the Filonenko−Borodich double-parameter foundation model. Piles and the surrounding soils were simplified as springs with different rigidities. According to static equilibrium of the model, the governing differential equation was established with consideration of the bending and tension of the reinforced mattress and the deformation of the pile and the soil. Using Bessel complex-variables functions, a deformation function of horizontal reinforced mattress was deduced. Then according to the deformation compatibility conditions, the formulas of the pile-soil stress ratio and settlement of the composite foundation were deduced relatively. Finally, two existing cases were employed for calculation and analysis. The influences of the tension force and the pile-soil stiffness ratio on the behavior of the composite foundation were also discussed respectively based on the current solution. The results show that the analysis results of the current solutions has a good agreement with the test results. The pile-soil ratio increases with the increase of the pile-soil rigidity ratio, composite modulus of reinforced mattress and tensile force of geosynthetic.
pile-net composite foundation; post-buckling; double-parameter foundation model; pile-soil stress ratio; settlement
10.11817/j.issn.1672-7207.2016.06.026
TU 470
A
1672−7207(2016)06−2007−08
2015−06−15;
2015−09−04
国家自然科学基金资助项目(51078138,51308208)(Projects(51078138, 51308208) supported by the National Natural Science Foundation of China)
赵明华,博士,教授,博士生导师,从事桩基础、软土地基处理研究;E-mail:mhzhaohd@21cn.com
