单轴拉伸下PVDF/POSS纳米复合材料的损伤模拟

赵连红，刘成臣，罗贤斌，王浩伟（中国特种飞行器研究所结构腐蚀防护与控制航空科技重点实验室，湖北荆门448035）

环境适应性设计与分析

单轴拉伸下PVDF/POSS纳米复合材料的损伤模拟

赵连红，刘成臣，罗贤斌，王浩伟
（中国特种飞行器研究所结构腐蚀防护与控制航空科技重点实验室，湖北荆门448035）

目的 研究PVDF及其氟化POSS纳米复合材料在单轴拉伸载荷下的损伤行为。方法 首先依据实验结果和细观力学均匀化方法，建立纯PVDF和三种不同POSS含量PVDF/POSS纳米复合材料的颗粒掺杂有限元模型，并通过在实体单元之间嵌入可破坏的内聚力单元来模拟损伤。结果 模拟得到的应力-应变关系与实验结果相吻合，证明了模拟结果的可靠性。损伤破坏的初始时间表明在破坏的初期阶段，POSS对于损伤有抑制作用，并且其效果随着POSS含量的增加而增强。损伤速度和最终的损伤面积和则表明质量分数在5%以下的POSS掺杂对于PVDF的损伤有抑制作用，并且随着POSS质量分数的增加其效果不断增强。当质量分数达到8%时，POSS的掺杂反而加速了PVDF的损伤。结论 POSS掺杂影响PVDF的损伤破坏，掺杂量对PVDF损伤破坏有抑制/促进作用，这一结果有助于理解实验所得到的力学参数的变化规律。

单轴拉伸；损伤；PVDF/POSS材料；内聚力单元；模拟

聚偏二氟乙烯（Poly Vinyli Dene Fluoride，PVDF）是最常用的压电聚合物，它有许多超越其他压电材料的优异性能，具有高化学稳定性、轻质量、高压电性、高延展性等优异特性，适合于制备各种传感器与作动器。在航天系统中有着十分广阔的应用前景和非常重要的战略价值，有望成为航天器各种智能系统的基本压电聚合物材料[1—2]。在实际应用过程中，PVDF材料却因为近地轨道原子氧的侵蚀和紫外线的辐射等因素而受到很大限制[3—4]。NASA与SANDIA公司合作在MISSE-6试验平台上测试的结果显示，在高能原子氧和紫外线环境工作3年后，PVDF薄膜的质量减轻到原来的40%左右[5]，并且在材料表面和内部均产生了非常明显的损伤。实验结果表明，普通的PVDF材料难以胜任太空的恶劣环境，高能原子氧、紫外线、高真空、剧烈的低温和高温等因素将不可避免地使得材料在较短的时间内（小于3年）失效。为了改进PVDF的性能，一种比较典型的方法是在PVDF表面镀上一层Al2O3（陶瓷）或SiO2保护层[6]。这种方法的问题在于陶瓷或氧化硅保护层会极大地降低PVDF的韧性，使其丧失柔韧性，并且工艺上偶然出现的缺陷会带来严重的基蚀现象。因此人们提出一种新颖的POSS杂化抗辐射加固PVDF材料（PVDF/POSS）的设计方案[7]。POSS是多面体低聚倍半硅氧烷（Polyhedral Oligomeric Silsesquioxane）的英文简称，是一类结构简式为（RSiO1.5）n（n≥4且为偶数，R为H、烷基、芳基或有机官能基团）的纳米尺度有机无机化合物（分子直径约为1.5 nm），它具有无机的硅氧（Si—O）笼型结构和有机官能团（R基团）[8]，因此既具有良好的力学、热力学和抗氧化性能，又具有很强的化学活性，非常容易与有机高分子材料、金属材料等通过化学反应相结合，能够大幅度地提高这类材料的性能[9]。因此，将POSS引入PVDF材料中有望提高PVDF的力学和抗氧化性能，从而解决众多在实际应用时所面临的问题。

在此前的工作中已经研究了不同的POSS化合物与PVDF之间的相互作用[10]，成功制备出了一种基于氟化POSS（FPPOSS）的PVDF/POSS纳米复合材料[11—12]，并得到了不同含量的POSS对PVDF力学性能的影响[13—14]。不管对于纯PVDF还是POSS增强的PVDF材料来说，了解外载荷作用下其内部的损伤行为是比较困难的。从实验角度来讲，很难在微观尺度下动态观察材料内部结构的演化过程；从计算的角度来看，分子（动力学）模拟方法囿于模型规模的大小，难以与实际情况相吻合，而传统的有限元模拟因为采用均匀化的模型很难模拟出损伤的产生和演化。在这样的背景下[15]，文中采用内聚力单元模型，结合实验数据来标定模型参数，并引入内聚力单元破坏法则，尝试采用有限元方法来模拟PVDF和PVDF/POSS纳米复合材料在单轴拉伸载荷下的损伤行为并分析POSS含量对于PVDF材料损伤行为的影响。考虑到柔性PVDF在空间环境下的服役状态大多数为张力作用下的展开形式，认为采用单轴拉伸载荷是具有现实意义的。

1　模拟模型

1.1颗粒掺杂模型

PVDF/POSS纳米复合材料中的氟化POSS随机分布在PVDF基体中，计算和实验结果均表明二者具有很好的相容性[10—13]，材料呈球晶形貌，未出现明显的相同分子团聚集、结块或团簇等现象[11—13]。从实验表征的结果来看[11—13]，四种材料（纯PVDF，POSS质量分数分别为3%，5%和8%的3种PVDF/POSS。以下简称这四种材料为纯PVDF，3%PVDF/POSS，5%PVDF/POSS和8%PVDF/POSS）的基本组成单元均为球晶颗粒，其颗粒典型直径分别约为90，120，150，180 nm。常温下氟化POSS的密度约为1.8 g/cm3，PVDF的密度取1.3 g/ cm3。依据实验结果，假设POSS在PVDF中均匀分布，根据四种材料POSS的质量分数和密度可求解出POSS的体积分数c1。根据纯PVDF和POSS单体的杨氏模量和体积模量，采用细观力学的均匀化方法可得到四种材料对应的等效力学参数。各种参数及结果见表1，此处POSS单体的力学参数采用了分子动力学模拟计算的结果[16]，等效杨氏模量采用E=9KG/（3K+G）来计算（假设材料为各向同性）。

表1　四种材料的等效模量及材料中POSS的体积分数Table 1 The equivalent moduli of the four kinds of materials and the volume fractions of POSS in the materials

模拟在ABAQUS软件下进行，采用的是二维模型。在建立颗粒掺杂模型的实体单元时用到表1中的等效力学常数。在定义颗粒掺杂模型时需要按照一定的顺序才能完成。首先要建立几何模型，即定义基体和POSS颗粒的几何位置，颗粒以圆形随机分布在基体中；然后对于颗粒和基体赋予不同的力学参数，并划分三角形网格，设定边界条件和外载；最后通过MATLAB软件在实体单元之间插入内聚力单元，完成内聚力单元的定义，从而能够描述二者之间的损伤和破坏过程。

1.2PVDF的粘弹性

PVDF是一种高聚物，具有粘弹性质[17]，并且这种性质在表征材料的损伤破坏中十分重要。针对PVDF的本构关系的特点，采用多个Maxwell单元并联的模型来描述其粘弹性，拉压松弛模量的形式可以表示为[18]：

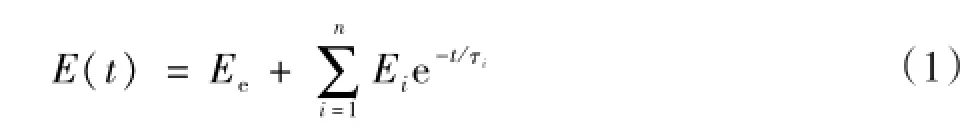
式中：Ee为平衡模量，亦即t→∞时模量E（t）的稳态值；Ei，τi是第i个Maxwell模型的松弛模量和松弛时间。根据Vinogradov[19]的方法得到储能模量E′（ω）、损耗模量E″（ω）和频率ω的关系，复模量E（*ω）为[18]：

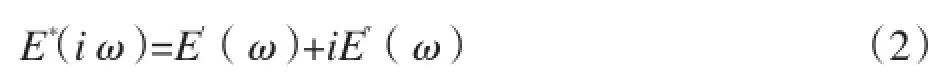
由松弛模E（ω）与复模量E（*iω）的关系[18]E（*iω）=iωE（ω），既而可以得到：

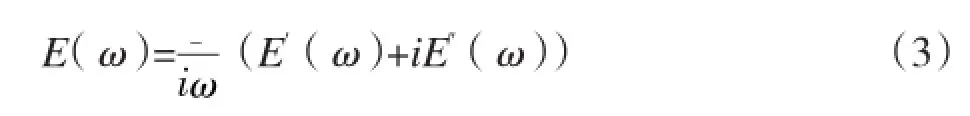
分别将四种材料的E′，E″[14]代入，经过傅立叶逆变换得到松弛模量时间函数：

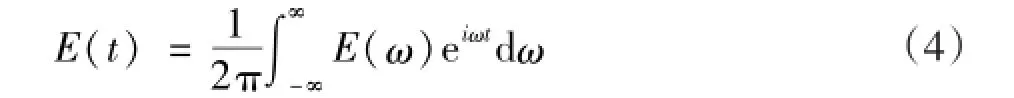
求出E（t）的表达式并用Prony级数表示，用式（1）的形式拟合曲线得到Ei，τi的值。由于可得到相对模量将运用到材料的粘弹性定义中。经过计算得到瞬态松弛模量E0的值为4.526 GPa，泊松比v=0.31。具体的Prony级数所对应的参数见表2。

表2　Prony级数中的参数Table 2 Parameters in the Prony series

1.3内聚力单元模型

在模拟中，损伤和破坏通过实体单元之间的内聚力单元来描述，因此需要定义内聚力单元破坏法则。图1描述了内聚力单元的张开量与所受内聚力的关系，从中可以了解内聚力单元开裂的特点。

图1表示，确定的内聚力破坏的参数有内聚力单元的破坏位移δn、最大的拉应力σmax以及其对应的张开位移δn、最大的切应力τmax，此外还涉及初始刚度 Kc。破坏位移δn、最大的拉应力σmax和初始刚度K可以通过单轴拉伸下的实验结果[14]来计算，而损伤变量D的演化则通过线性损伤演化模型来求解：

式中：δmax为加载过程中有效位移的最大值；损伤变量D的范围为0～1。D=0意味着材料没有任何损伤，而D=1则对应着材料完全破坏，无任何承载能力。模拟中首先以三角形实体单元类型来划分网格，然后在实体单元中插入厚度为零的二维四节点内聚力单元。具体形成过程如图2所示[20]。

图1　内聚力-张开量关系Fig.1　The relationship between the cohesive force and the traction-separation for cohesive elements

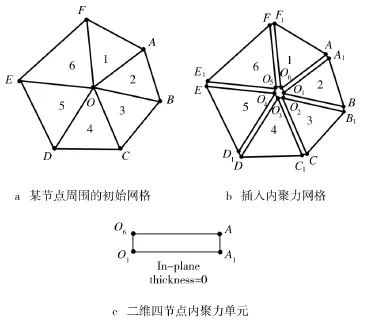
图2　插入内聚力单元到初始网格的过程Fig.2　The procedure of inserting cohesive elements into the initial meshes

文中模拟所构建的四种材料的模型如图3a所示，模型尺寸为2.85 mm×0.68 mm，其中圆孔代表随机分布的POSS颗粒，其含量按表1中的POSS体积分数c1来设定，加载时采用位移荷载的形式，加载的最大位移为0.56 mm（对应名义应变为20%），加载的时间为0.35 s，而模型的左端采用固定边界条件。图3b显示的是对应的初始结构网格划分，然后依据内聚力单元的生成方式，在实体单元中加入内聚力单元。文中涉及到3种不同形式的内聚力单元，分别为PVDF基体内聚力单元、POSS颗粒内部的内聚力单元以及PVDF基体与POSS颗粒边界上的内聚力单元。各内聚力单元的对应参数由实验结果[13]计算得到，见表3。每种材料模拟采用的边界条件及外部位移荷载都是相同的，具体损伤情况通过计算损伤面积、损伤发生的初始时间以及损伤发展的速度三方面来描述。其中损伤面积定义为破坏的内聚力单元的面积（内聚力单元发生张开位移后面积大于零），而具体损伤程度则由单元损伤参数SDEG（scalar stiffness degradation）来描述。SDEG与损伤变量D相对应，其值在0～1之间，该值的大小表明损伤的程度，当SDEG=1时单元完全破坏。

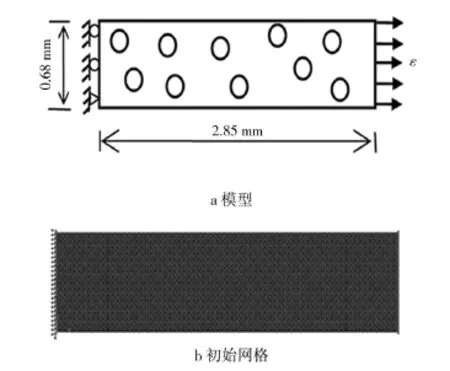
图3　模型及初始网格Fig.3 The sketch map of the model and its initial grids

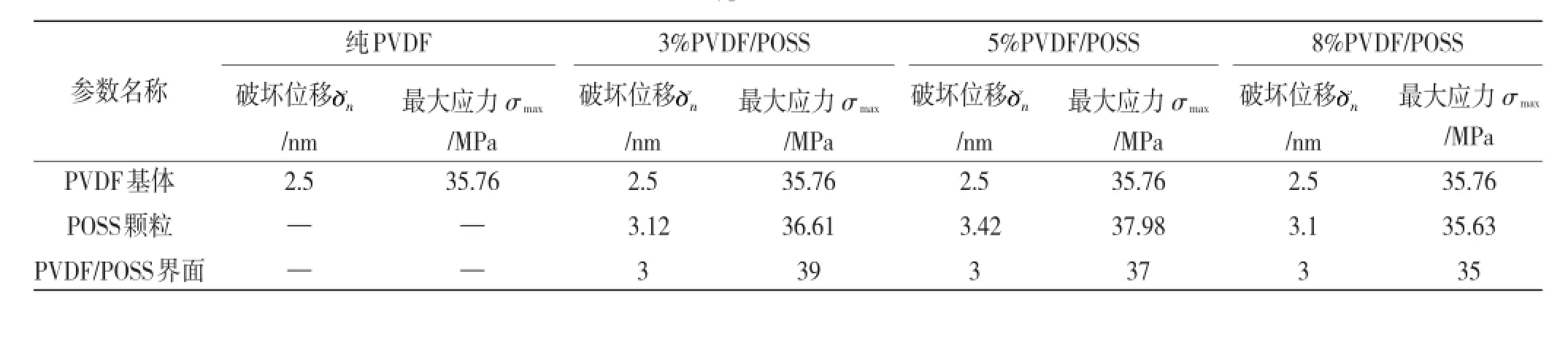
表3　不同材料中三种类型的内聚力单元参数Table 3 Parameters of the three types of cohesive elements in different materials

2　结果与讨论

首先计算了四种材料在单轴拉伸作用下的应力-应变关系。一方面，应力-应变关系是较容易获得的数据之一；另一方面，模拟的结果可以和实验数据进行直接比较以检验模拟结果是否可靠，并继而判断模型和模拟参数是否设置正确。图4显示了实验和模拟分别得到的四种材料的应力-应变曲线，其中实验结果来自文献[13]，模拟结果只显示到实验中试样发生断裂的最小应变处。从图4的结果可以看到，模拟结果与实验结果吻合得非常好。这种结果是可以预料的，因为模拟所用的模型参数大部分来源于实验数据。这一结果也表明文中的模拟在技术上是可信的。

文中的主要目的是研究实验中难以观察的发生在材料内部的损伤现象，因此需要对其他有关损伤的变量进行考察。图5显示了四种材料在完成加载后整个模型中SDEG>0.7的损伤云图。从图5中可清晰地看出，从纯PVDF到5%PVDF/POSS，损伤范围的分布是逐渐缩小的，但是8%PVDF/POSS的损伤范围又开始急剧增加，甚至高于纯PVDF模型中的损伤范围。图5中损伤面积的数值可计算，计算结果表明，四种材料的损伤面积分别为1517S，1457S，1205S和1608S（S为单个内聚力单元的面积），损伤面积的数值其实就是模型中损伤的内聚力单元数目。计算的结果也印证了基于图像的判断，即损伤范围的大小顺序为：5% PVDF/POSS<3%PVDF/POSS<纯PVDF<8%PVDF/ POSS。

图4　实验与与模拟所得到的四种材料的应力-应变关系Fig.4 The stress-strain relations of four materials obtained from the experiments and the simulations

通过比较四种模型在同一加载条件下达到某一相同损伤量（取损伤累积值为100）的时间来判定初始损伤时间，损伤速度则可以由累积SEDG值-时间曲线来得到。图6显示了加载过程中累积损伤随时间的变化关系。按照前面关于初始损伤时间的定义，由图6中放大的部分可清晰地看出初始损伤时间是随着POSS含量的增加而延迟的。这表明加入POSS有延缓PVDF损伤发生的效果，亦即在破坏的初期阶段，POSS对于损伤是有抑制作用的，并且抑制效果随着POSS含量的增加而增强。当加载时间到达0.19 s时，3% PVDF/POSS的损伤速度突然增加，大于其他三种材料的损伤速度；当加载时间到达0.28 s时，8%PVDF/POSS的损伤速度迅速增加，并使得其累积损伤量大于其他三种材料，最终产生了最大的损伤面积。四种材料最终的累积SEDG值分别为2429.13，2279.18，2096.91和2668.45（图5显示了分布情况）。

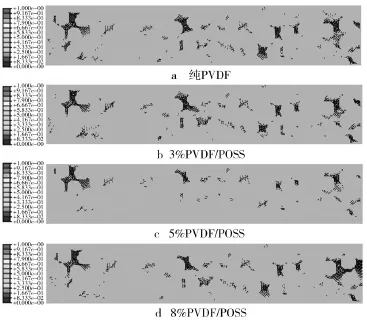
图5　四种材料的损伤分布（SDEG>0.7）(a)纯PVDF(b)3%PVDF/ POSS(c)5%PVDF/POSS(d)8%PVDF/POSSFig.5　The damage of four materials(SDEG>0.7)(a)neat PVDF(b) 3%PVDF/POSS(c)5%PVDF/POSS and(d)8%PVDF/POSS

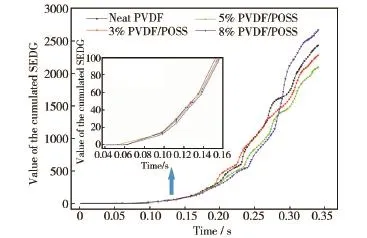
图6　四种材料的累积SEDG值随时间的变化关系Fig.6 The curves of the cumulated SEDG of four materials vs.time

结果表明，质量分数为0%～5%的POSS掺杂有助于抑制PVDF在单轴拉伸载荷下的损伤行为，而含量为8%的POSS掺杂则不利于PVDF对损伤的抑制作用，降低了PVDF的抗拉强度。这些趋势与实验和模拟所得到的四种材料的力学参数变化趋势类似。产生这一结果的原因在于POSS所体现出来的有机无机特性。一方面POSS相比PVDF基体具有更高的强度，但另一方面POSS单体与PVDF基体有很好的相容性，体现出较好的形变协调性。少量的POSS掺杂会在PVDF基体中产生均匀的增强相，并且不会给体系的韧性带来太大的影响，因此当POSS的含量小于5%时，体系的累积损伤是随着POSS含量的增加而降低的。当POSS的含量过高时，虽然POSS作为增强相会增加体系的强度，并且POSS与基体之间仍然很好地相容，但是过高含量的POSS也意味着二相POSS粒子之间的基体含量越来越少，使得粒子和基体之间的应力和应变变得难以协调，反而促进了损伤的发生。

3　结论

文中依据实验结果和细观力学均匀化方法，建立了氟化POSS与PVDF结合后形成的颗粒掺杂的有限元模型，并采用内聚力单元的形式来模拟单轴拉伸载荷下的损伤行为。模拟的结果与四种材料的实验结果相吻合，证明了模拟结果的可靠性。结合模拟的结果以内聚力单元损伤面积、损伤起始时间、损伤速度三个方面表征了四种材料的损伤特性。

结果表明，在破坏的初期阶段，POSS对于损伤有抑制作用，并且其效果随着POSS含量的增加而增强。最终的损伤结果表明，质量分数在5%以下的POSS掺杂对于PVDF在单轴拉伸下的损伤有抑制作用，并且随着POSS质量分数的增加，其抑制作用增强。当质量分数达到8%时，POSS的掺杂反而加速了PVDF的损伤，表明过高比例的POSS不利于增强PVDF的抗拉强度。氟化POSS单体本身所体现出来的有机无机特性以及与PVDF基体之间的相容性有助于解释这些现象。文中的结果也表明采用内聚力单元模型的有限元方法能够有效地应用于研究材料的损伤行为。

[1]TUZZOLINO A J，ECONOMOU T E，CLARK B C，et al.Dust Measurements in the Coma of Comet 81P/Wild 2 by the Dust Flux Monitor Instrument[J].Science，2004，304（5678）：1776—1780.

[2]MCDONNELL J A M，BURCHELL M J，GREEN S F，et al. The Stardust Dust Flux Monitor[J].Advances in Space Research，2000（25）：335—338

[3]翟睿琼，姜利祥，田东波，等.国外热塑性树脂复合材料低轨道原子氧环境效应进展[J].装备环境工程2015，12（3）；64—69.

ZHAI Rui-qiong，JIANG Li-xiang，TIAN Dong-bo，et al.Review on Research Progress of AO Effects on Thermoplastic Composites at Abroad[J].Equipment Environmental Engineering，2015，12（3）；64—69.

[4]CELINA M C，DARAGAVILLE T R，et al.Piezoelectric PVDF Materials Performance and Operation Limits in SpaceEnvironments[J].Materials for Space Applications，2005，851：449—460

[5]DARGAVILLE T R，CELINA M，MARTIN J W，et al.Evaluation of Piezoelectric Pvdf Polymers for Use in Space Environments.II.Effects of Atomic Oxygen and Vacuum Uv Exposure [J].Journal of Polymer Science Part B：Polymer Physics，2005 （43）：2503—2513

[6]MINTON T K，WU B H，ZHANG J M，et al.Protecting Polymers in Space with Atomic Layer Deposition Coatings[J].Acs Applied Materials&Interfaces，2010，2（9）：2515—2520

[7]CHINCARINI Andrea，et al.On the Preparation and Application of Novel PVDF-POSS Systems[J].J Mater Sci，2009，44：1764—1771.

[8]SCKWAB J J，LICHTENHAN J D.Polyhedral Oligomeric Silsesquioxane（POSS）-Based Polymers[J].Applied Organometallic Chemistry，1998;12：707—713.

[9]BROOWN A S.New Possibilities for High-Temperature Polymers[J].Aerospace America，1999，37（1）：30—33.

[10]ZENG Fan-lin，SUN Yi，ZHOU Yu，et al.Molecular Simulations of the Miscibility in Binary Mixtures of PVDF and POSS Compounds[J].Modelling and Simulation in Materials Science and Engineering，2009，17，075002.

[11]LIU Yi-zhi，SUN Yi，ZENG Fan-lin，et al.Morphology，Crystallization，Thermal and Mechanical Properties of Poly（Vinylidene Fluoride）Films Filled with Different Concentrations of Polyhedral Oligomeric Silsesquioxane[J].Polymer Engineering&Science，2013，53（7）;1364—1373.

[12]LIU Yi-zhi，SUN Yi，ZENG Fan-lin，et al.Effect of POSS Nanofiller on Structure，Thermal and Mechanical Properties of PVDF Matrix[J].Journal of Nanoparticle Research，2013，15：2116.

[13]ZENG Fan-lin，LIU Yi-zhi，SUN Yi，et al.Nanoindentation，Nanoscratch and Nanotensile Testing of Poly（vinylidene fluoride）-Polyhedral Oligomeric Silsesquioxane Nanocomposites [J].Journal of Polymer Science Part B：Polymer Physics，2012，50（23）：1597—1611.

[14]ZENG Fan-lin，SUN Yi，ZHOU Yu，et al.A Molecular Dynamics Simulation Study to Investigate the Elastic Properties of PVDF and POSS Nanocomposites[J].Modelling and Simulation in Materials Science and Engineering，2011，19：025005.

[15]赵保平，孙建亮，蔡俊文，等.航天动力学环境的最新进展与技术展望[J].装备环境工程，2015，12（3）；8—14.

ZHAO Bao-ping，SUN Jian-liang，CAI Jun-wen，et al.Recent Development and Prospect of Astrodynamic Environmental Technology[J].Equipment Environmental Engineering，2015，12（3）；8—14.

[16]李君.POSS纳米杂化材料的分子动力学模拟方法与力学性能研究[D].哈尔滨：哈尔滨工业大学，2011.

LI Jun.Molecular Dynamics Simulation and Mechanical Properties of POSS Nano Hybrid Materials[D].Harbin：Harbin Institute of Technology，2011.

[17]VINOGRADOV A M，SCHMIDT V H，TUTHILL G F，et al. Damping and Electromechanical Energy Losses in the Piezoelectric Polymer PVDF[J].Mechanics of Materials，2004，36：1007—1016.

[18]杨挺青，罗文波.粘弹性理论与应用[M].北京：科学出版社，2004.

YANG Ting-qing，LUO Wen-bo.Viscoelastic Theory and Applications[M].Beijing：Science Press，2004.

[19]VINOGRADOY A M，HOLLOWAY F.Dynamic Mechanical Testing of the Creep and Relaxation Properties of Polyvinylidene Fluoride[J].Polymer Testing，2000，19：131—142.

[20]YANG Z J，SU X T，CHEN J F，et al.Monte Carlo Simulation of Complex Cohesive Fracture in Random Heterogeneous Quasi-brittle Materials[J].International Journal of Solids and Structures，2009，46（17）：3222—3234.

Finite Element Simulations of Damage Behaviors of PVDF/POSS Nanocomposites under Uniaxial Tensile Loads

ZHAO Lian-hong，LIU Cheng-chen，LUO Xian-bin，WANG Hao-wei
（Structure Corrosion Protection and Control of Aviation Science and Technology Key Laboratory，China Special Vehicle Reach Institute，Jingmen 448035，China）

Objective To study the damage behaviors of PVDF and its fluorinated POSS nanocomposites under uniaxial tensile loads.Methods The particle-mixed finite element models of neat PVDF and three kinds of PVDF/ POSS nanocomposites with different POSS contents were firstly built according to the experimental results and the homogenization method in the mesoscopic mechanics.Then the damage behaviors were simulated after inserting the destructible cohesive elements into the solid elements.Results The simulated stress-strain relationships were in good agreement with the experimental results,which proved that the simulations in this article were reliable.The starting time of the damage revealed that at the initial stage the POSS was able to restrain the damage and the effect became obvious when the POSS content increased.And the final damage areas and the damage speed showed that the POSS would restrain the damage when its content was below 5%.In this case,the restraining effect was even stronger when the POSS content was increasing.However,the addition of POSS would accelerate the damage speed when the POSS content reached to 8%.Conclusion Doped POSS influences the damage of PVDF,the doping amount has the inhibition/ promotion effect on damage and failure of PVDF.These results are very helpful to understand the variation rules of the mechanical properties observed in the experiments.

uniaxial tensile;damage；PVDF/POSS nanocomposites；cohesive elements；finite element simulation

2015-09－07；Revised：2015-09－16

10.7643/issn.1672-9242.2016.01.015

TJ04；O345

A

1672－9242（2016）01－0079-07

2015-09－07；

2015-09－16

国家自然科学基金资助项目（11102053）；哈尔滨市科技创新人才研究专项资金资助项目（2012RFQXG001）

Fund：Supported by the National Natural Science Foundation of China（11102053）and Special Funds for Scientific and Technological Innovation Talents in Harbin（2012RFQXG001）

赵连红（1988—），男，湖北荆门人，工程师，主要研究方向腐蚀环境航空航天材料损伤行为研究。

Biography：ZHAO Lian-hong（1988—），Male，From Jingmen，Hubei，Engineer，Research focus：damage behavioral of aerospace material in corrosive environment.