多进制GMSK频谱分析及解调算法
2016-10-11李春腾张曙霞李崇远
李春腾,张曙霞,李崇远
(海军工程大学 电子工程学院,湖北 武汉 430033)
多进制GMSK频谱分析及解调算法
李春腾,张曙霞,李崇远
(海军工程大学 电子工程学院,湖北 武汉 430033)
多进制GMSK具有较大的频谱效率优势,对提高通信的效能有十分重要的意义。首先在二进制GMSK信号频谱的基础上,对多进制GMSK信号的频谱进行简要介绍,并对其进行比较,其次借鉴二进制GMSK信号的产生和解调思路,研究了多进制GMSK的产生算法及解调方式,并提出了对多进制GMSK信号的准最佳最大似然比解调算法,并对该算法进行仿真,结果发现该算法能够取得较好的误码性能。
多进制;GMSK;频谱;解调算法
0 引言
由于GMSK的窄带宽和恒包络特性,它获取的频谱效率与MSK[1]相比要高很多,因此人们针对GMSK的调制解调展开了深入的研究,采用非相干解调与相干解调[2]在GMSK的信号中均有应用[3-4]。美国的Bruce提出了多进制GMSK调制的算法[5],在衰减信道条件下将网格编码调制和多进制GMSK调制结合在一起,对补偿网络进行了引进,这样系统性能就不会受码间串扰更多的影响,误码率显著降低,但Bruce并未给出解调方法,这也是本文研究的重点。
在数字通信技术不断发展的过程中,随着不断提高的通信需求,传输的信号会受到信道带限与信道非线性的影响。在研究和分析这些技术的过程中,人们重点关注节省频谱的方式以及如何高效应用频谱。对基带码元信号进行多进制的调制,属于一种非常有效的办法,多进制GMSK作为恒包络技术的一种可应用于非线性的信道条件下,能够保证频带范围比较小[6-7]。
1 多进制GMSK信号的调制
假设数字基带信号表示为:
(1)
式中,T代表的是码元维持时间的长短,In则为包含信息的序列,用二进制表示,g(t)表示的是高斯最小频移键控(GMSK)脉冲,其中包含带宽参数值B,用公式表达如下:

(2)
(3)
在实际应用中,式(2)可以当作是由经过高斯低通滤波器的矩形脉冲rect(t)所生成的,如式(4):
g(t)=h(t)*rect(t);
(4)
h(t)为滤波器的冲激响应为:
(5)
可以通过傅里叶变换来获取滤波器的频率特征:
H(f)=exp[-(ln2/2)(f/B)2]。
(6)
2 多进制GMSK频谱比较与分析
首先对二进制GMSK信号的频谱进行分析。首先是读入分析参数,包括符号的总长度N,对信号的采样频率fs,码元的传输速率Rb和一个码元周期的采样点数,即过采样比OSR;然后产生伯努利分布的01二进制序列,序列需进行极性转换,变为双极性的非归零二进制序列NRZ;接着对该序列进行差分编码的预编码;对预编码后的比特序列要进行串并转换,展宽后变成I路和Q路两路比特流;接下来的工作是高斯滤波器的设计,首先是高斯滤波器的3 dB带宽参数BT值设定为0.3,然后根据高斯脉冲的阶数确定高斯成形脉冲的延时,最后由滤波器函数确定出滤波器系数;接着是将I路和Q路信号组成复信号I+jQ,同设计好的高斯滤波器系数卷积,并去除滤波器带来的延时,得到高斯脉冲积分后的值;取积分后的实部和虚部对应和正弦型加权函数相乘,分别得到基带信号的I路和分量,最终合成复基带GMSK信号;然后是对合成的复基带信号进行分段,对每段分别作傅里叶变换,对每段的结果取平均;最后根据采用频率fs和每段的数据长度,控制画出其基带信号的频谱[11]。
对频谱分析主要从数据分段数和每段数据长度进行着手。具体来说,分段数和每段数据长度成制约关系,由图1可以看出,当分段数越少时,每段数据长度越长,频谱的能量泄漏越少,频率分辨率也就提高了,但各个频率成分的“毛刺”会有所增加,这是因为分段数较小时样本数少,分段取平均不能很好地反映各个频率分量实际大小,所以在频谱分析中要对数据分段数和每段数据长度的取值作一定折中,以便更好地进行频谱分析。

图1 不同分段数对频谱分析的影响
多进制GMSK信号频谱的分析区别于二进制主要体现在信号产生这一方面。对于四进制,可将符号比特作电平映射,得到四进制的电平值,即sym的NRZ序列;另外调制指数通过改变I路和Q路的正弦型加权函数的相关参数,指导多进制复基带GMSK信号的产生。
研究和分析不同调制阶数M对信号频谱的影响程度,分别从二进制GMSK(BGMSK)、四进制GMSK(4GMSK)和八进制GMSK(8GMSK)的功率谱密度着手分析,对于频率均作归一化处理,且对于高阶的调制也均折算为1 bit的功率谱密度。首先整体上由于是复数基带,几个功率谱的正负频率略有不对称。对比特归一化后,对比不同阶数的功率谱密度,可以发现阶数越高,功率谱带外衰减更快,主瓣宽度更窄,以主瓣衰减10 dB为参考线,可得出不同阶数GMSK信号的主瓣宽度之比l2GMSK:l4GMSK:l8GMSK约为1:0.708 0:0.598 5,这说明多进制GMSK调制的1 bit带宽更窄,频率效率越高。这和调制指数h存在一定关系,当调制阶数越高,h越小,相位越连续,带外功率谱越低,带外功率谱下降越快,但随着阶数提高获得的1 bit带宽相对增益会减少。
3 多进制GMSK信号的解调
由于多进制GMSK信号调制[12-13]涉及的较高阶数带来的计算和系统设计的复杂程度,所以对其解调算法的探究除需借鉴二进制GMSK的相关解调方式,还要充分考虑多进制调制系统的自身特点,找到最优的解调方式。本节提出一种基于准最佳最大似然算法的软判决检测,这种软判决算法是所研究和推广的多进制GMSK解调算法的重点。
以最佳接收机的二进制GMSK解调理论为基础,向多进制解调理论进行推广,对在几个信号传输间隔中,利用互相关的办法,通过GMSK信号记忆的特征,可有如下解调思路的分析。可把接收信号进行如下表示:
r(t)=s(t,d1,Dk)+n(t)。
(7)
这里,可以把首个待检测码元计为d1,把观察序列的n-1个码元计为Dk={d2,…,dn}。从相干检测的角度来说,可以把初始相位φ设置为零,通过最佳接收机能够得到最大似然比:

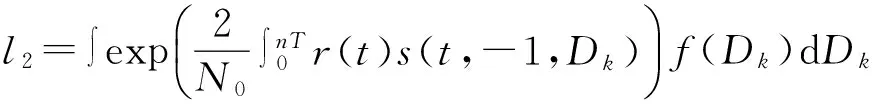
⋮
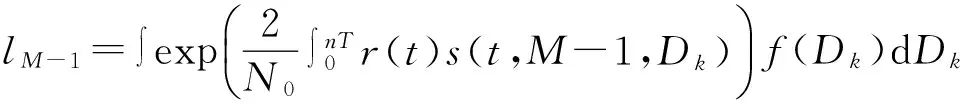
(8)
f(Dk)用来表示被观察序列Dk的离散的概率密度函数(PDF),∫f(Dk)dDk则用来表示n-1重积分∫∫…∫f(d2)f(d3)…f(dn)dd2dd3…ddn,其中每个离散PDFf(dμ)是一系列冲激函数δ的组合:
(9)
Dk序列所有可能数量为Mn-1=m种,所以对D的积分可等价于:
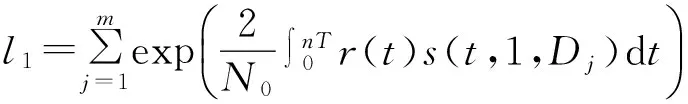

⋮
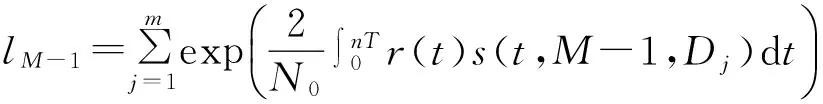
(10)
由上面的l值,可以做出相关的判决,最终得到d1。采取准最佳解调的思路:假如所观测序列可以设定出一个长度为n,在进行检测时,每一次检测都对各个组的码元长度为n的所接收的波形进行相关性计算。在去除指数运算和累加运算基础上,取出Mn路的相关输出最大的那一路的序列,则当前这一组码元的值判为当前这一路输入的参考信号s对应的码元序列。
通过以上分析,可得4GMSK误码率的程序分析框图,如图2所示。其中BT为高斯滤波器的3 dB带宽参数,Tb为码元时间,N为码元序列长度,OSR为过采样比,T为每次观测序列的长度,K=4T表遍历个数,SNRpBit为归一化1比特信噪比参数。首先根据给定观测序列长度遍历所有K个序列的波形,接着在不同信噪比条件下,生成N×T序列长度对应的波形,加噪声,然后利用准最佳最大似然比算法,进行波形检测,最后输出其误码率。
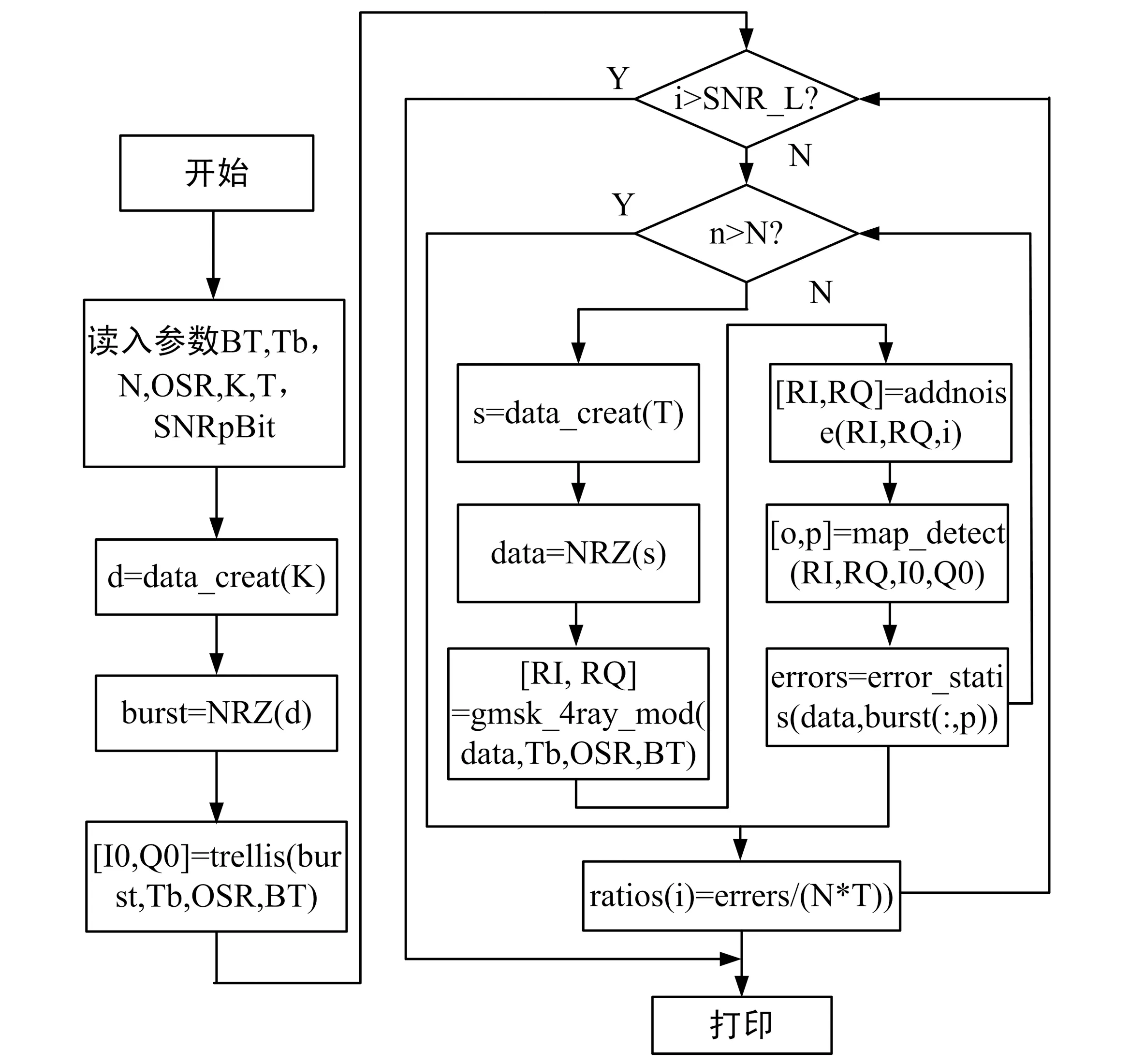
图2 4进制GMSK误码率分析流程
对于多进制调制,其最佳误码率性能表达式为[5]:
(11)
把不同进制的误码率均折算为1 bit码元的误码率进行比较。并通过MATLAB对其进行仿真[14],结果如图3所示。通过图3可知,调制阶数M在不断地增加,传输1 bit码元所需的信噪比也随之增加。这和调制指数h存在一定关系,当M增大时,h越小,相位越连续,而且载波的终值相位状态增加,从相位星座图上来看,当信噪比小于一定门限值时,噪声容限减小,模糊了相位终值状态点之间的差别,接收机很难准确判定调制时的相位终值状态及其转移路径,故性能有所下降。通过上节分析可知,为使频带的利用率得到进一步提升,且1 bit带宽随着阶数提高而减小,可以利用多进制GMSK进行调制来获取误码率和频谱效率的折中效益。
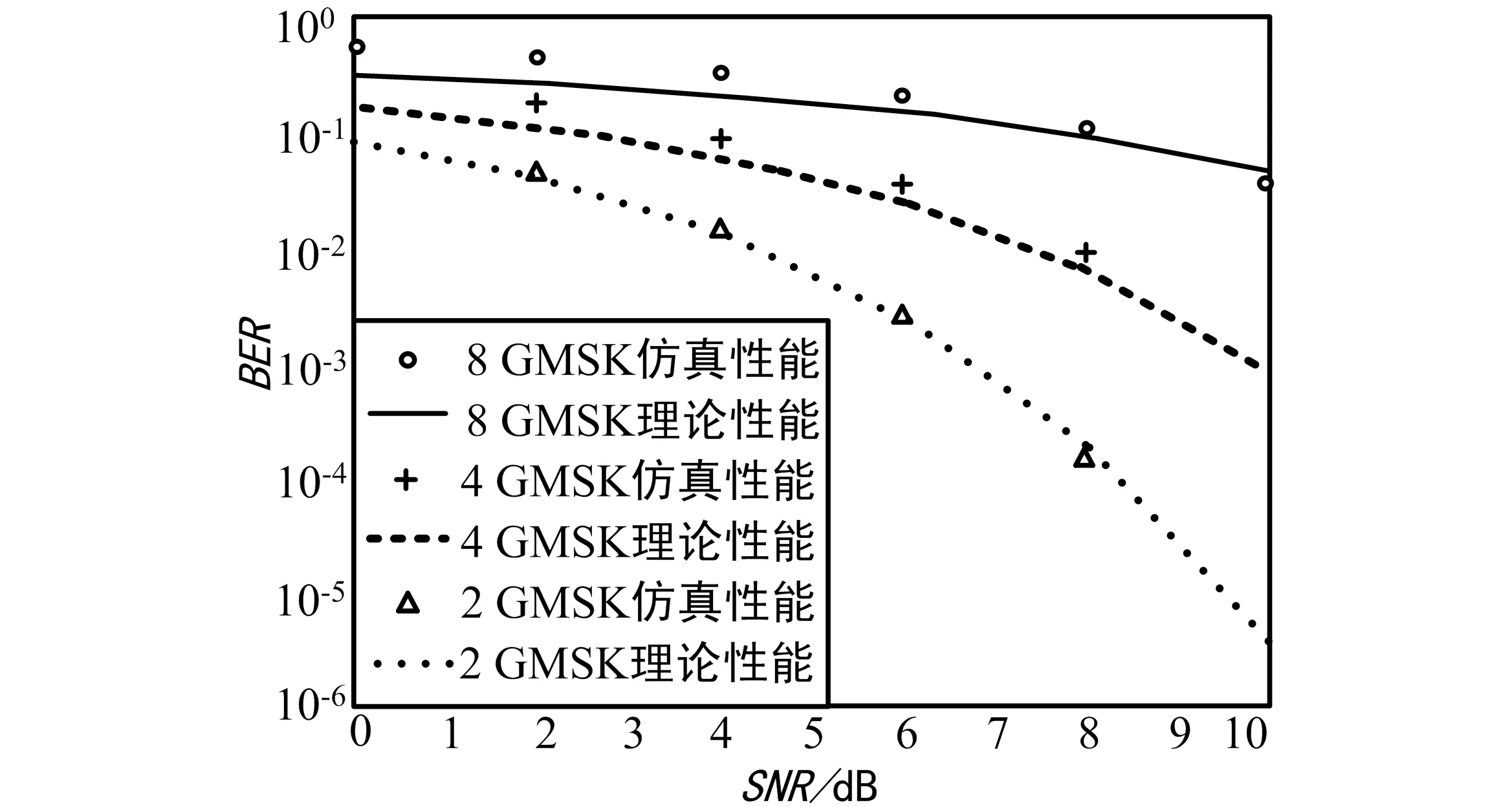
图3 不同进制的GMSK误码性能
4 结束语
本文提出了多进制GMSK信号的产生及解调算法,比较和分析了不同阶数的GMSK频谱,结果显示不同阶数GMSK信号的主瓣宽度之比l2GMSK:l4GMSK:l8GMSK约为1:0.708 0:0.598 5,这说明多进制GMSK调制的1 bit带宽更窄,频率效率更高。还对多进制GMSK信号如何解调进行了研究和分析,主要是基于最佳接收机的准最佳最大似然算法的检测。
GMSK因其良好的频谱特性受到广泛关注,除了进行多进制方面的研究,还可考虑结合其他恒包络调制方式[15],如SOQPSK、TFM等,实现联合调制,可使系统性能进一步优化。
[1]Bims H V,Cioffi J M.Trellis Coding with M-ary MSK Constraints[J].IEEE Global Telecommunications,1989,18(21):1546-1550.
[2]Gee L L.Threshold Detection Performance Of GMSK Signal With BT=0.5[J].IEEE Transactions on Communication,1998,2(23):515-519.
[3]熊于菽.GMSK调制解调技术研究[D].重庆:重庆大学,2007:24-32.
[4]丁兴文.基于维特比算法的GMSK信号非相干解调技术研究[J].遥测遥控,2011,32(1):18-21.
[5]Cochran B.Development and Application of M-ary Gaussian Minimum Phase Shift Keying modulation[J].IEEE International Conference on Communications,1995,21(3):1805-1810.
[6]Bims H V,Cioffi J M.Trellis Coding with M-ary MSK constraints[J].IEEE Global Telecommunications,1989,18(21):1546-1550.
[7]樊昌信,曹丽娜.通信原理(第6版)[M].北京:国防工业出版社,2010:241-251.
[8]Murota K,Hirade K.GMSK Modulation for Digital Mobile Radio Telephony[J].IEEE Transactions on Communications,1981,29(7):1044-1050.
[9]丁阳,韦志棉.高斯最小频移键控的实现方法研究和仿真[J].无线电工程,2006,36(3):32-34.
[10]U S Patent and Trademark Office.SICOM,INC.Data Communication Modulation with Managed Intersymbol Interference[S].
[11]马雯.连续相位调制信号的功率谱及带宽特性研究[J].现代电子技术,2010(5):39-41.
[12]赵彦惠.基于相位累加实现GMSK调制的技术分析[J].无线电工程,2013,43(3):20-23.
[13]郑海荣.多调制指数连续相位调制解调算法的研究[D].哈尔滨:哈尔滨工业大学,2012:16-45.
[14]杨允军,武传华.用MATLAB实现GMSK信号的产生与解调[J].无线电工程,2005,35(9):58-60.
[15]陈敬乔.一种新的GMSK调制器的设计与实现方法[J].无线电工程,2014,44(7):79-82.
Spectrum Analysis and Demodulation Algorithm of M-ary GMSK
LI Chun-teng,ZHANG Shu-xia,LI Chong-yuan
(Electronic Engineering College,Naval University of Engineering,Wuhan Hubei 430033,China)
M-ary GMSK has a large advantage in spectrum efficiency,which is very important for improving the communication efficiency.Based on the signal spectrum of binary GMSK,the signal spectrum of M-ary GMSK is introduced and compared with binary GMSK,the generation algorithm of M-ary GMSK and demodulation methods are studied with the help of binary algorithm.A suboptimal maximum likelihood ratio demodulation method for M-ary GMSK is proposed.The simulation results show that the performance of this method has good performance in BER.
multi-ary;GMSK;spectrum;demodulation method
10.3969/j.issn.1003-3114.2016.05.10
引用格式:李春腾,张曙霞,李崇远.多进制GMSK频谱分析及解调算法[J].无线电通信技术,2016,42(5):38-41.
2016-05-20
李春腾(1992—),男,硕士研究生,主要研究方向:通信理论与技术。张曙霞(1968—),女,副教授,主要研究方向:信息网络信号处理。
TP391.4
A
1003-3114(2016)05-38-4
