一种改进的变步长LMS算法及在车内降噪中的应用
2016-10-11崔婷玉陈卫松丁绪星
崔婷玉,陈卫松,丁绪星,武 闯,张 丽
(安徽师范大学 物理与电子信息学院,安徽 芜湖241000)
一种改进的变步长LMS算法及在车内降噪中的应用
崔婷玉,陈卫松,丁绪星,武闯,张丽
(安徽师范大学 物理与电子信息学院,安徽 芜湖241000)
为了提高传统最小均方(LMS)算法的收敛速度,减小稳态误差,基于Sigmoid函数,提出一种改进步长因子μ的方法。该方法通过建立步长因子μ和误差信号e之间的非线性函数关系,并利用指数函数表示误差信号e和可控参数,实现对步长因子μ进行调整。算法收敛初期步长因子μ相对较大,实现加快算法收敛速度的目的;算法收敛后期适度减小稳态阶段步长因子μ,以达到减小算法稳态误差的目的。将该算法应用于车内噪声的有源控制,并与LMS算法进行仿真比较分析。仿真结果表明,相对于传统LMS算法,该算法有效地加快了收敛速度,同时提高了系统的稳定性。
LMS算法;SVSLMS算法;变步长;车内噪声
0 引言
随着人们生活质量的提高,人们对于乘用车乘坐舒适度的要求也越来越高。对于乘用车来说,车内噪声主要来源于发动机和车身震动辐射到车内的噪声,以400 Hz以下的低频噪声为主。自适应主动噪声控制系统在低频噪声领域已获得广泛的应用,是一种有效的乘用车车内降噪方法。在自适应主动噪声控制系统中,多采用LMS算法。LMS算法的步长μ是固定值,步长μ取值大,收敛速度快,但稳态误差较大,反之,步长μ取值小,稳态误差较小,但收敛速度越慢。所以,LMS算法的收敛速度和稳态误差是一对矛盾。
为解决该问题,研究人员提出很多种改进的变步长LMS算法,文献[1]中提出的基于Sigmoid函数变步长SVSLMS算法是其中具有代表性的变步长LMS算法之一。该算法具有较快的收敛速度,但是Sigmoid函数在误差信号e(n)接近零时变化太大,容易产生较大的稳态误差。文献[2]中针对SVSLMS算法的不足进行改进,通过减小稳态阶段的调整步长μ,有效地减小稳态误差,但是与SVSLMS算法相比,改进后的算法计算复杂度高,收敛速度提高较小。文献[3]中提出一种基于步长和误差信号之间的非线性关系的双曲线正切函数变步长LMS算法,该算法有较小的稳态误差,但是收敛速度提高较小。文献[4]中提出一种步长和误差信号呈正弦函数关系的变步长LMS算法,解决了LMS算法不能同时具有较快收敛速度和较小稳态误差的矛盾,但是参数选取缺乏理论依据,只能通过实验来获得。文献[5-13]中用不同的方法提出步长因子μ和误差信号e之间的非线性函数关系的变步长LMS算法,这些算法在改变步长μ(n)时均遵循基本调整原则:在初始收敛阶段,采用大的步长,加快收敛速度,稳态阶段,采用较小的步长,降低稳态误差。针对这种调整原则,本文在文献[2]算法基础上提出一种新的变步长LMS算法,能够有效地提高初始阶段收敛速度,减小稳态误差。
1 改进的变步长LMS算法
文献[1]提出一种基于Sigmoid函数的变步长LMS算法-SVSLMS算法,其步长μ(n)为:

(1)
式中,e(n)为误差信号,α、β为常数。
SVSLMS算法的收敛范围0<β<2/λmax(λmax是输入信号自相关矩阵的最大特征值),克服了传统LMS算法的收敛速度慢的不足,但是在稳态阶段的步长较大,容易引起稳态失调。
文献[2]在文献[1]基础上提出了一种改进的变步长LMS算法,步长μ(n)为:

(2)
式中,α为控制函数形状的常数,β为控制函数取值范围的常数。
该算法符合变步长算法调整准则,收敛范围0<β<1/λmax,克服了SVSLMS算法的稳态误差较大的不足,但是收敛速度提高较小。

(3)
在初始收敛阶段,为了加快收敛速度,将文献[2]变步长函数中固定值1调整为可控值exp(α),当α>0,exp(α)>1,所以在条件相同的情况下,改进后的算法在初始阶段步长较大,为符合当误差函数e(n)取零时,步长也为零,将文献[2]算法中的固定值2调整为h/exp(α)。因为μ(n)<[β·exp(α)],所以本文算法β·exp(α)的最大值[β·exp(α)]max=1/λmax,本文算法收敛条件为α>0,0<[β·exp(α)]<1/λmax。
图1中图(a)、(b)是3种算法的步长和误差关系比较图。

(a)α=1.5,β=0.000 05,3种算法比较曲线
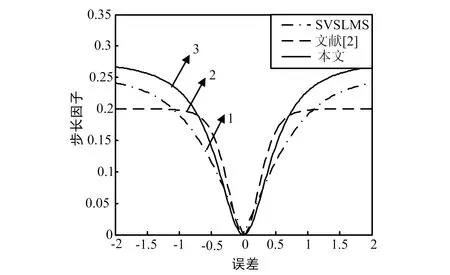
(b)α、β取不同值,3种算法比较曲线图1 3种算法步长与误差关系比较曲线
图中,曲线1代表SVSLMS算法,曲线2代表文献[2]算法,曲线3代表本文算法,为了便于比较,将图1(a)中3种算法的参数α和β取相同值,α=1.5,β=0.000 05.初始阶段误差值e(n)相同时,曲线3的步长最大,使得本文算法收敛速度最快,在稳态阶段,误差值e(n)相同时,曲线3的步长小于曲线1但大于曲线2,稳态误差小于SVSLMS算法但大于文献[2]算法。所以本文算法克服了SVSLMS算法稳态误差大的问题,同时也弥补了文献[2]算法收敛速度提高较小的不足。
为了从数学角度更好地分析本文算法,根据本文参数变化规律α,β均取较大值,有利于加快本文算法初始收敛速度。图1(b)中SVSLMS算法取值为α=2,β=0.5情况下,文献[2]算法最佳取值为α=6,β=0.2,本文算法最佳取值为α=1.7,β=0.05,h=4,图1(b)显示在初始阶段,误差值e(n)相同时,曲线3的步长最大,使得本文算法收敛速度最快,在稳态阶段,误差值e(n)相同时,曲线3的步长最小,获得稳态误差最小,所以本文算法优于另外2种算法。
图2、图3和图4分别是当参数h、α和β取不同值时,变步长μ(n)和误差函数e(n)的关系图。从图2中可以看出,h在初始阶段对步长影响较小,它对步长函数的底部有很大的影响,也就是说,在稳态阶段,它对步长有较大的影响。如果h的值越大,步长在曲线底部改变得就越慢,误差函数e(n)趋于零时,步长μ(n)越小,稳态误差越小。反之,h的值越小,稳态误差越大。所以结合文献[2]和仿真结果取h=4。图3和图4表明,α和β参数的调整对初始阶段步长影响较大,决定了算法的收敛性能,但α和β的调整对步长大小的影响不同,α和β参数均需调整。当α和β取值越大,初始阶段的步长就越大,算法的收敛速度就越快。相反,α和β取值越小,初始阶段的步长就越小,算法的收敛速度就越慢。所以本文算法的步长参数调整规则如下:在满足算法不发散的前提下,选取较大的α、β和较小的h,可使算法具有较快的收敛速度和跟踪速度。反之,选取较小的α、β和较大的h,会使算法具有较小的稳态失调。实际应用中,根据具体的情况,选择适当的h、α和β值,才能达到最佳的效果。

图2 h改变时μ(n)和e(n)的关系图

图3 α改变时μ(n)和e(n)的关系图

图4 β改变时μ(n)和e(n)的关系图
2 仿真研究结果分析
2.1收敛性能和抗噪能力仿真比较分析
为了验证本文算法在不同信噪比条件下的收敛性能和抗噪能力,对本文算法和另外3种算法进行仿真对比实验。仿真条件如下:为说明文中算法对处理信号的选取具有一般性,输入信号选用被噪声信号干扰的随机信号,其中噪声信号r(n)为方差为1、均值为零的高斯白噪声,滤波器阶数为8。为了平衡收敛速度和稳态误差,固定步长LMS算法的步长μ=0.00 001。由于另外3种算法的α和β取值不具有一般性,在满足0<[β·exp(α)]<1/λmax范围内随机取相同值α=1.5,β=0.00 005。α和β取值如图1(a)所示,4种算法在信噪比为10和15时误差函数的MATLAB仿真结果如图5所示。
图5(a)和(b)中曲线1代表LMS算法,曲线2代表SVSLMS算法,曲线3代表文献[2]算法,曲线4代表本文算法,在图5(a)中,曲线4误差e(n)收敛于n=200,稳态误差e(n)<1,另外3条曲线n=200未收敛,稳态误差e(n)>1。图5(b)中,曲线4收敛于n=50,另外3条曲线n=50时未收敛,曲线4稳态误差e(n)最小。仿真结果可以得出,相同条件下,曲线4的收敛速度要最快,稳态误差最小,结果进一步验证了本文算法收敛速度快和抗噪能力强的特点。与固定步长的LMS算法相比,本文算法的计算量增加了四次指数运算、两次除法运算和四次加法运算。


图5 不同信噪比条件下,4种算法收敛曲线对比
2.2车内噪声控制仿真分析
为了分析本文算法在车内降噪中的应用,在车内录取一段噪声信号导入MATLAB程序中,采用LMS算法和本文算法对车内噪声信号进行自适应滤波降噪。
仿真条件如下:读取噪声信号前1 000个采样点,选取输入信号和期望信号中的前100个采样点作为训练点构建自适应滤波器,随机选取未参与训练的采样点进行自适应滤波降噪处理。经过多次实验,LMS算法的固定步长最佳取值为μ=0.1,本文算法参数α,β取值为α=4,β=5。基于LMS算法和本文算法的自适应滤波降噪结果如图6所示,图4中细实线为经过自适应LMS滤波器处理后的误差信号波形,粗虚线为经过本文算法构建的自适应滤波器处理后的误差信号波形。

图6 2种算法的误差信号波形
图6中分别是LMS算法和本文算法在自适应滤波过程中的误差波形曲线,它表明了自适应滤波过程中误差的变化过程。由图6可知自适应LMS滤波中的误差波形(细实线)达到稳态误差的速度明显比本文算法误差曲线(粗虚线)要慢,同时本文算法在迭代过程中的误差值明显小于LMS算法。
通过建立基于LMS算法和本文算法的自适应滤波器,并应用于车内噪声的主动控制的结果比较表明,本文算法抵消原始车内噪声效果较好,对LMS算法在迭代步长取值矛盾问题有所改善,具有更快的算法收敛速度和较小的稳态误差。
3 结束语
提出了一种改进的变步长LMS算法,针对传统LMS和SVSLMS算法在收敛速度和稳态误差方面存在的不足,该算法在SVSLMS算法的基础上,通过调节可变参数值,达到动态选取步长大小的目的,有效提高了算法的收敛速度,降低了算法的稳态误差,同时提高了算法在车内降噪应用中的降噪能力。该算法在后期需要在算法复杂度方面进行研究改进,减小相应计算量。
[1]覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997,12(3):171-174.
[2]陈泳,田金鹏,刘燕平.一种新的变步长LMS自适应滤波算法[J].电子测量技术,2015,38(4):27-31.
[3]Wu X,Gao L,Tan Z.AnImproved Variable Step Size LMS Algorithm[C]//IEEE 2013 International Conference on Measurement,Information and Control (ICMIC),2013:533-536.
[4]余荣平,张心光,王岩松,等.车内噪声主动控制变步长LMS算法[J].噪声与振动控制,2015,35(1):123-126.
[5]朱宏光.一种改进的变步长LMS自适应算法[J].无线电通信技术,2010,36(4):13-15.
[6]LI X B,Fan Y Y,Peng K.A Variable Step-Size LMS Adaptive Filtering Algorithm[C]//IEEE 2009.WiCom '09.5th International Conference on Wireless Communications,Networking and Mobile Computing,2009:1-4.
[7]Yan Y,Zhao J,Wang Z,et al.An Novel Variable Step Size LMS Adaptive Filtering Algorithm Based on Hyperbolic Tangent Function[C]//2010 International Conference on Computer Application and System Modeling (ICCASM),2010,14:V14-233-V14-236.
[8]Kwong R H,Johnston E W.A Variable Step Size LMS Algorithm[J].Signal Processing IEEE Transactions on,1992,40(7):1633-1642.
[9]Majdar R S,Eshghi M.A New Variable Step-size Normalized PBS_LMS Algorithm[C]//IEEE 2011 IEEE International Conference on Computer Applications and Industrial Electronics (ICCAIE),2011:168-171.
[10]李昌利,沈玉利.一种改进的变步长LMS算法[J].无线电通信技术,2009,35(1):53-54.
[11]孙柏昶,秦建存.LMS算法瞬态收敛特性研究[J].无线电通信技术,2006,32(2):26-28.
[12]陈卫东,王长焕,解静.基于自适应滤波的宽带阵列信号处理技术[J].无线电通信技术,2009,35(5):16-18.
[13]曹斌芳,何怡刚,李建奇.改进型最小均方算法的仿真比较及在语音提取中的应用[J].噪声与振动控制,2008,28(2):98-101.
An Improved Variable-step-size LMS Algorithm and Its Application for Reducing Noise in Vehicles
CUI Ting-yu,CHEN Wei-song,DING Xu-xing,WU Chuang,ZHANG Li
(College of Physics and Electronic Information,Anhui Normal University,Wuhu Anhui 241000,China)
In order to improve the convergence speed and reduce the steady-state error of the traditional least mean square (LMS) algorithm,a method is proposed to improve the step factor μ based on the Sigmoid function.In the algorithm,a nonlinear relationship is established between the step factor μ and the error signal e.The error signal e and controllable parameters are expressed in exponential form to adjust the step size factor μ.The step factor μ is relatively large in the initial convergence stage to speed up convergence of the algorithm.In the later convergence stage,the step factor μ is moderately reduced to achieve the purpose of reducing the steady-state error.The proposed algorithm is applied to the active control of vehicle interior noise.The control effect of the algorithm is compared with that of the LMS algorithm.The simulation results show that the proposed algorithm accelerates the convergence rate and improves the stability of the system.
least mean square (LMS) algorithm;sigmoid variable step-size LMS (SVSLMS) algorithm;variable step size;vehicle interior noise
10.3969/j.issn.1003-3114.2016.05.20
引用格式:崔婷玉,陈卫松,丁绪星,等.一种改进的变步长LMS算法及在车内降噪中的应用[J].无线电通信技术,2016,42(5):80-84.
2016-06-06
国家自然科学基金项目(61401004);安徽师范大学研究生科研创新与实践项目(2014yks063)
崔婷玉(1991—),女,硕士研究生,物联网技术专业,主要研究方向:有源噪声控制。陈卫松(1973—),男,副教授,硕士生导师,主要研究方向:音频信号处理及噪声控制。
TN911.23
A
1003-3114(2016)05-80-5
