基于改进SPRT的多重响应序贯分支筛选法

施　文，冷凯君，毕　娅

(1.华中科技大学管理学院，湖北武汉430074；2.湖北经济学院湖北物流发展研究中心，湖北武汉430205)



基于改进SPRT的多重响应序贯分支筛选法

施文1，2，冷凯君2，毕娅2

(1.华中科技大学管理学院，湖北武汉430074；2.湖北经济学院湖北物流发展研究中心，湖北武汉430205)

针对仿真实验中多重响应序贯分支法(MSB)不能验证单个因子对所有响应效应显著性这一不足，在改进Wald序贯概率比检验(SPRT)的基础上提出了一种新的多重响应序贯分支法(简称IMSB).该方法在仅增加少量仿真次数并在保证统计效力的基础上，即可获取单个因子对所有响应的效应显著性信息.蒙特卡洛对比仿真表明IMSB是切实可行的，在完全保证仿真实验效力的同时准确获取了因子对所有响应的效应显著性判断，且较传统的针对单个响应的SB法减少了大量的仿真次数，该方法在大型复杂仿真系统的后仿真分析中具有良好的实际应用价值.

筛选；序贯分支；多重响应；仿真实验

1　引　言

由于仿真技术在解决实际复杂问题时具备的独特优势，越来越多的学者[1，2]采用仿真建立数学模型(计算机代码).目前，针对确定性仿真的计算实验(computer experiments)[35]或针对随机性仿真的(随机)仿真实验(simulation experiments)[6，7]被认为是解决复杂系统设计问题的唯一有效工具[8].相较于真实实验，仿真实验(本文主要研究随机性仿真)经常含有较多的因子或称仿真输入.管理学中帕累托(80/20)原理和实验设计(design of experime nts，DOE)理论中的稀疏效应(sparsity-of-effects)定理[9]都表明，仿真系统中一般只有少量因子对响应[7]有关键影响.筛选就是要识别出对响应起着最重要作用的少部分因子[7].

现有筛选设计方法主要有经典的二水平设计，频域设计，超饱和设计及群组筛选设计，多数方法源于传统DOE而被引入到仿真实验之中，它们都把仿真看成黑箱(black-box)处理[6，7].本文聚焦于序贯分支(sequential bifurcation，SB)筛选法，区别于上述传统的筛选设计，SB是专门针对计算/仿真实验而提出的群组筛选法，能充分利用计算机的序贯特性，在满足一定的假设条件下，该方法最具效率与效力[7，10，11].近年来，许多学者将SB应用于如爱立信供应链设计[11]，半导体生产流程优化[12，13]，汽车零部件供应物流优化[14]等实际的管理科学问题中，解决了大型复杂仿真系统的优化设计问题.SB首先将仿真模型的所有因子聚合到一个组(group)，然后检验该组的聚合效应(一阶主效应和)是否显著，若显著，则将该组分割为两个子组(subgroup)，即分支；否则，判定该组无重要因子，停止SB.重复类似的步骤：重要的(子)组不断细分，去掉不重要的(子)组，直至筛选出重要因子.其中SB针对任一(子)组都重复两个固定的步骤：1)计算群组效应值；2)通过统计推断方法检验该群组效应值的显著性.

SB早期的研究采用传统的t-检验判定群组的显著性.Bettonvil等[15]最早提出SB的理论框架并应用到一个生态环保的确定性仿真模型中.Cheng[16]，Kleijnen等[11]将SB拓展至随机仿真领域，后者解决了一个爱立信供应链设计问题.而后，部分学者引入新的方法来提供统计检验的精度，Wan等[12，17]，在SB的基础上，将效应检验分为两个阶段，每一阶段采用假设检验来控制两类错误(α和β)发生的概率.Shen等[18]提出一个可控的序贯分式设计(controlled sequential factorial design)方法，该方法将传统分式实验设计与序贯假设检验相结合.Shen等[19]通过引入Fold-over设计进一步改进了CSFD的效率与效力.Wan等[13]利用Wald序贯概率比检验(sequential probability ratio test，SPRT)来控制两类误差概率，该方法提高了实验的效率与效力.还有Frazier等[20]研究SB群组筛选过程中最优的分组(group-splitting)策略问题.Shi等[10]首次研究了多重响应的仿真因子筛选问题，提出了多重响应序贯分支(MSB)法并采用SPRT控制两类错误的概率.

由上述文献可以看出，作为一种较新的仿真实验因子筛选法，SB已成为学术界的热点并在理论和应用上取得了一定的成果.许多学者都对SB第二个固定步骤展开了研究，从起初的t-检验，到最新的SPRT检验.尽管Shi等[10]已将SB方法拓展到多重响应领域并提出MSB方法，但MSB方法在SPRT效应检验过程中无法顾及到所有的响应，而仅能笼统地判断该群组或因子对某一响应是否重要.例如，在100个因子、2个响应的仿真筛选设计中，假如MSB方法判定出第1号因子为重要因子.但是该因子具体对某个响应重要或者对两个响应都重要，MSB方法则无法作出判断.实际中，决策者更希望洞察每一因子对所有响应的效应大小，即第1号因子到底是属于哪一个或哪些响应的重要因子，从而更全面系统地把握企业的运营行为，进而制定行而有效的针对性方案.针对这一不足，本文提出一种基于新的SPRT的多重序贯分支方法(简称IMSB方法)，使得能识别出因子对每一响应的作用大小.蒙特卡洛仿真结果表明IMSB方法仅在增加较少仿真次数并保证实验效力的基础上完成因子对所有响应的影响大小的判断，显示所提方法切实可行，具有较好的理论成果与应用价值.

2　基于改进SPRT的IMSB方法

2.1IMSB方法的数学假设

本文所提的IMSB方法采用的符号见表1.

IMSB方法基于以下三个假设，它们也是SB方法和MSB方法的基本假设[10，12，13，15，1719].

假设1对响应l，一个足拟的元模型(meta-model)是具有噪声的二阶多项式，即

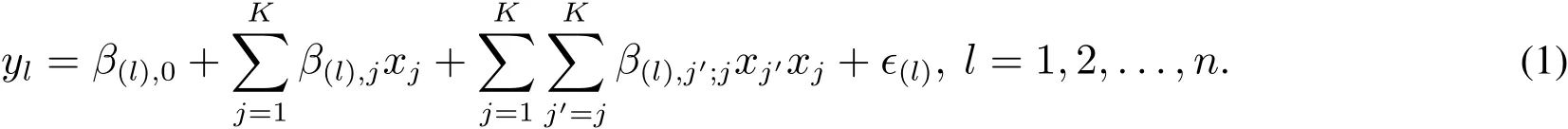
式(1)实际是源于泰勒展开式的经典多项式元模型，xj=(zj-(hj+lj)/2)/((hj-lj)/2)为标准化后的值，即-1≤xj≤1，其中zj为xj的原始值，其上下限分别为hj和lj，j=1，2，...，K，标准化后因子效应与尺度无关从而可以相互比较.响应l的截距为β(l)，0，K个主(一阶)效应为β(l)，j，K(K-1)/2个两因子交互效应为β(l)，j，j′，j＜j′，K个纯二次效应为β(l)，j，j，ϵ(l)为0均值，方差为的噪声.

假设2单个因子对响应l作用的方向(单调性)已知，即β(l)，j≥0或β(l)，j≤0，j=1，2，...K.

假设2是群组筛选设计的基本假设[6，21]，它避免了某组中的不同因子间主效应值的相互抵消.基于此假设可以定义因子的高低水平，使得某因子从低水平(-1)调整到高水平(+1)时响应单调递增，其中β(l)，j=0表示响应也可能保持不变.实际中这一假设确实成立，参见文献[11，13，15]的案例.

假设3如果单个因子无显著主效应，其二阶效应也不显著[23]，即

表1　符号说明Table 1 Major symbols and definitions

2.2IMSB方法的数学描述

IMSB方法首先需要确定群组j′-j对响应l的一阶主效应和，进而才能通过统计推断判定该群组是否具有显著性.以下定义1给出了目前所有序贯分支筛选(SB方法和MSB方法)计算响应l的一阶主效应和的方法，然而，绝大多数学者[6，7，1119]研究的是只存在单个响应(n=1)的仿真系统，即不存在式(2)等号两端的下标“(l)”.当响应数为多个时(n＞1)，如何高效地获得所有响应的一阶主效应和变得尤为重要.一种直观的方式是用SB法把n个响应视为n个单独的因子筛选问题，然后对所有响应依次逐个计算，但这一方式显然非常低效且当n较大时所需仿真次数也随之急剧增加(见第3节数值分析).IMSB方法采用Shi等[10]的方法得到不同响应的一阶主效应和，因为Shi等[10]针对多重响应提出了batch组的概念(定义3)，基于这一概念在不增加额外仿真次数的基础上可同时得到某batch组所有响应的一阶主效应和.为方便起见，以下的定理1和定理2给出了Shi等[10]同时计算响应l和l′的群组效应和的公式，引理1和引理2为同时计算最后阶段响应l和l′的单个因子效应值的公式，其中l/=l′=1，2，...，n.更多的细节和证明参见文献[10].

调整因子j从水平L(l)，j至H(l)，j使得响应l(非严格)单调增加1这一变化可能导致其它响应l′(l/=l′)(非严格)单调减少，因为某一特定因子对不同响应可能具有相反的单调性..

Batch组指当该组内所有因子从L(l)，j改变至H(l)，j时，n个响应(非严格)同时单调增加或减少，即在该batch组内，不同因子间的效应没有相互抵消(某个响应具有同一效应符号，即+或-).

定理1[10]如果因子j′至j在同一batch组且响应l和l′具有相同的单调性，则响应l和l′群组效应估计量分别为

引理1[10]如果因子j从水平L(l)调整至水平H(l)使响应l和l′同时增加或减少，则该因子对响应l和l′效应估计量分别为

定理2[10]如果因子j′至j在同一batch组且响应l和l′具有相反的单调性，则响应l和l′群组效应估计量分别为

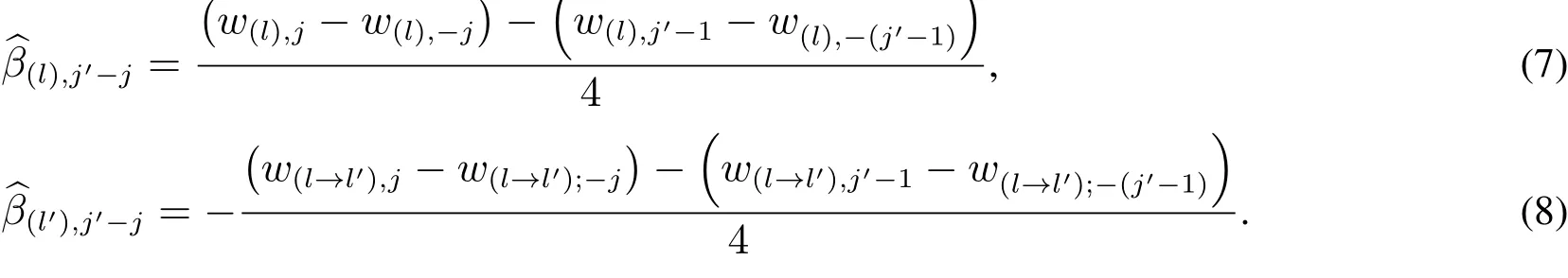
引理2[10]如果因子j从水平L(l)调整至水平H(l)使响应l增加而使响应l′或减少，则该因子对响应l和l′效应估计量分别为

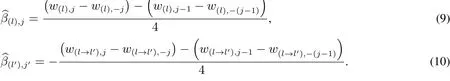
2.3IMSB方法的SPRT

传统的t-检验可用以估计群组或单个因子主效应的显著性，即检验式(2)中β(l)，j′-j或β(l)，j，IMSB法采用改进的Wald序贯概率比检验(SPRT)检验被估群组或单个因子效应的显著性.SPRT用于早期阶段的群组(多个因子)或后期单个因子的效应检验，相比SB法采用的t-检验[11，15，21]，SPRT可控制两类错误的发生概率[10，13]，即

Pr｛群组j′-j为重要群组，Pr｛群组j′-j为重要群组

图1描述了n=2时IMSB法的SPRT流程.该图中实线和虚线所构成的两个三角形分别代表响应1和2的SPRT连续迭代区域，当迭代过程中的迭代点处于所属三角形的内部时，无法判断效应的显著性，需要增加一次仿真抽样(仿真重复)，而只有迭代出上或下任意一条边界时才可判断.

图1　IMSB的SPRT步骤Fig.1 Procedure of IMSB’s SPRT

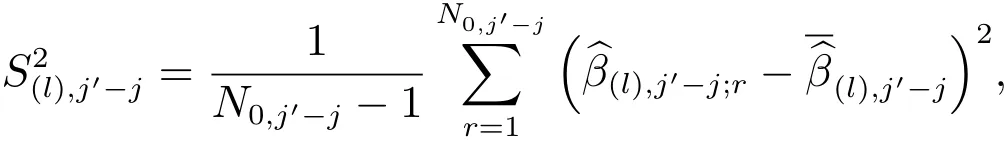
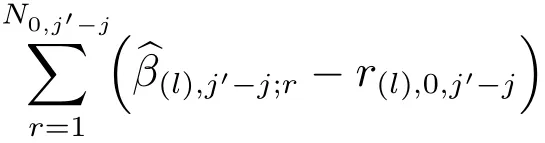
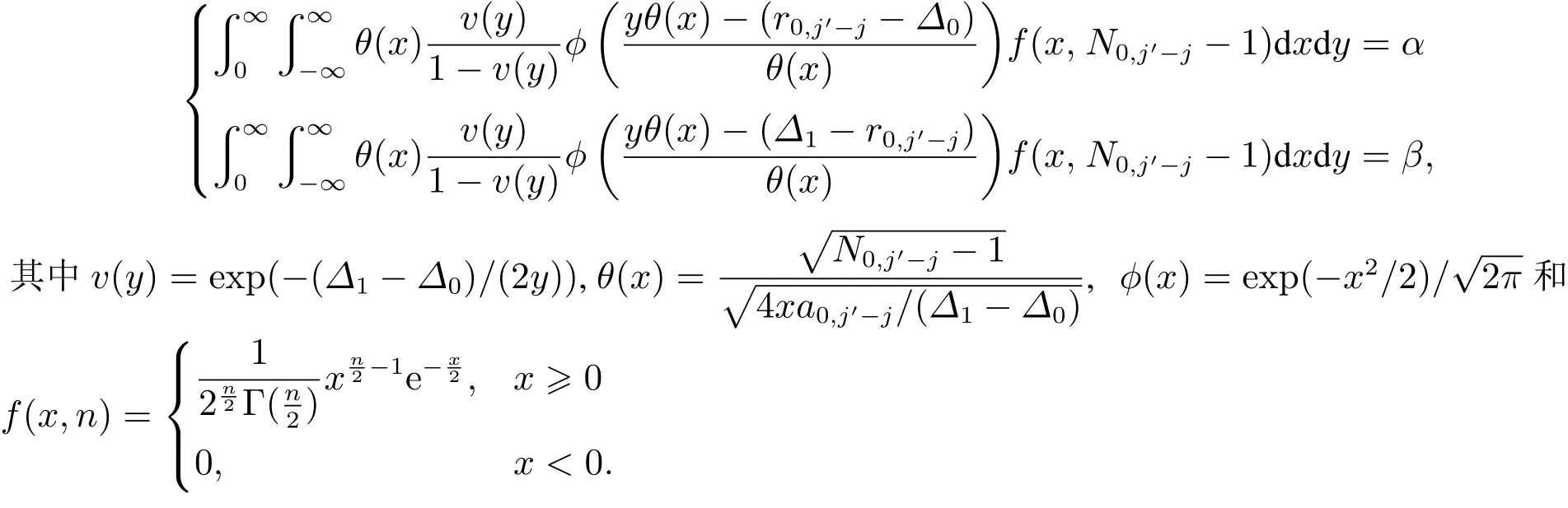
IMSB迭代包含如下的具体步骤.

初始化 r←N0，j.

步骤1如果r≤M(l)，j，l=1，2，

步骤1.2.1与步骤1.1.1相同；

步骤1.2.2与步骤1.1.2相同；否则r←r+1，重复步骤1，直至步骤2；

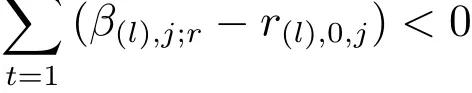
步骤2.1.1与步骤1.1.1相同；

步骤2.1.2与步骤1.1.2相同；否则r←r+1，重复步骤2，直至步骤3；

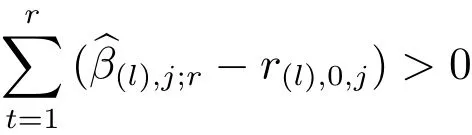
步骤2.2.1与步骤1.1.1相同；

步骤2.2.2与步骤1.1.2相同；否则r←r+1，重复步骤2直至步骤3；

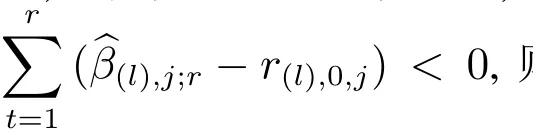
3　蒙特卡洛仿真

本文主要是对现有SB和MSB进行的改进，因而蒙特卡洛仿真的目的在于体现所提的IMSB方法在仿真实验效率和效力的优势.由于不同方法仿真实验效率和效力比较是仿真实验领域常见的做法[7]，因此，蒙特卡洛仿真从这两方面进行.对于随机仿真筛选设计而言，效率越高，表明该方法所用到的仿真重复次数越少；效力越高，表明该方法能更准备地判定出重要因子.3.1节和3.2节正是从“效率”和“效力”两方面展开.为了便于比较，尽可能地参照文献[10]数值实验中的参数设置，即K=100，n=2，q=2，∆0=2，∆1= 4，N0；1-100=5，p=5，α=0.05，γ=0.9，Var(ϵ1)=52或102(见表2第2，3列).

3.1IMSB法，SB法和MSB法实验效率比较

本文比较了3种方法在8个因子组合下的实验结果，每一组合都考虑两个batch组：第3列等式右端“±”表示因子对响应1有正效应，对响应2有负效应，例如，第1个因子组合表示100个因子中，第1，2，99，100号因子|β(l)，j≥0|，即，|β(l)，1|=|β(l)，99|=2，其它因子β(l)，j=0(j=1，2，99，100).其中第1，2号因子对响应1和2同时为正效应，第99，100号因子对响应1有正效应，但对响应2为负效应.

表2列出了IMSB法，传统SB法及MSB法在不同因子组合下完成整个筛选程序所需的仿真次数.

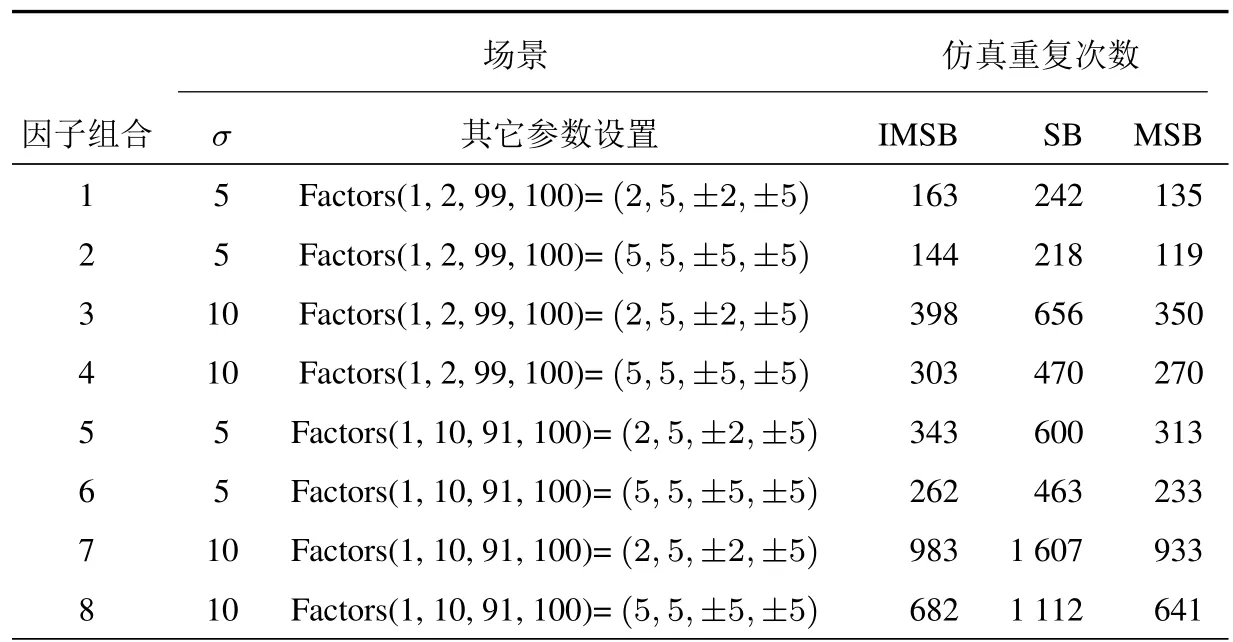
表2　IMSB，MSB及SB仿真次数比较Table 2 Simulation replicates comparisons for IMSB，MSB and SB

由该表可知，1)当σ较小时(σ=5)时，3种方法所需的仿真次数较少，说明筛选实验的效率(仿真次数)与仿真系统的稳定性有关，系统越稳定(σ越小)，筛选实验效率越高；反之σ越大)需要较多的仿真次数；2)重要因子的效应值大小及在所有因子中的分布密集状况也对实验效率有直接影响，|β(l)，j|越大(=5)且分布越集中时(因子组合1～4的重要因子集中分布在两端，因子组合5～8的重要因子分散分布)，所需的仿真次数也较少；3)综合以上3方面属性(σ，|β(l)，j|及重要因子分布密集度)可发现，3种方法最少的仿真次数均出现在第两个因子组合，该组合σ=5，|β(l)，j|=5且集中分布在两端；最多仿真次数出现在第7个组合；4)由表2还可看出，在所有的8个组合中，MSB仿真次数＜IMSB仿真次数≪SB仿真次数.这说明在面对多重响应时，MSB法和IMSB法都大大地提高了传统SB法筛选时仿真实验的效率，减少了仿真次数.另外，尽管MSB法相较于IMSB法次数有所减少，但减少幅度十分有限，仅为且随着所需实验次数的增加，二者有明显相互接近的趋势，如983和933，又如682和641，这主要是因为IMSB法所需的绝大部分实验已与MSB法重叠，而仅需较少的实验次数完成对剩余响应的判断.

3.2IMSB法SB法和MSB法实验效力比较

(R1，R2)，(R1，R2)，(R1，R2)和(R1，R2)分别表示某个因子最终判定可能的4种结果，其中粗体表示对某一响应有显著性影响，非粗体则为非显著性影响.例如，对于第1个因子组合中的第1号因子而言(该表第3列)，(R1，R2)=0.002，即IMSB法在1 000次筛选实验中最终有2次(=1000×0.002)判定因子1对响应1显著，对响应2不显著；(R1，R2)=0.098，即有998次(=1000×0.988)次判定因子1同时对两个响应无显著影响.又如对于第99号因子(该表第5列)，(R1，R2)=0.006，即IMSB法在1 000次筛选实验中最终有6次(=1000×0.006)判定因子99对响应1显著，对响应2不显著；(R1，R2)=0.011，即有11次(=1000×0.011)判定因子99对响应1不显著，对响应2显著；(R1，R2)=0.983，即有983次(= 1000×0.983)判定同时对两个响应不显著.

表3　IMSB，MSB法及SB法筛选结果Pr｛DI｝统计效力比较Table 3 Efficacy comparisons among，MSB and SB

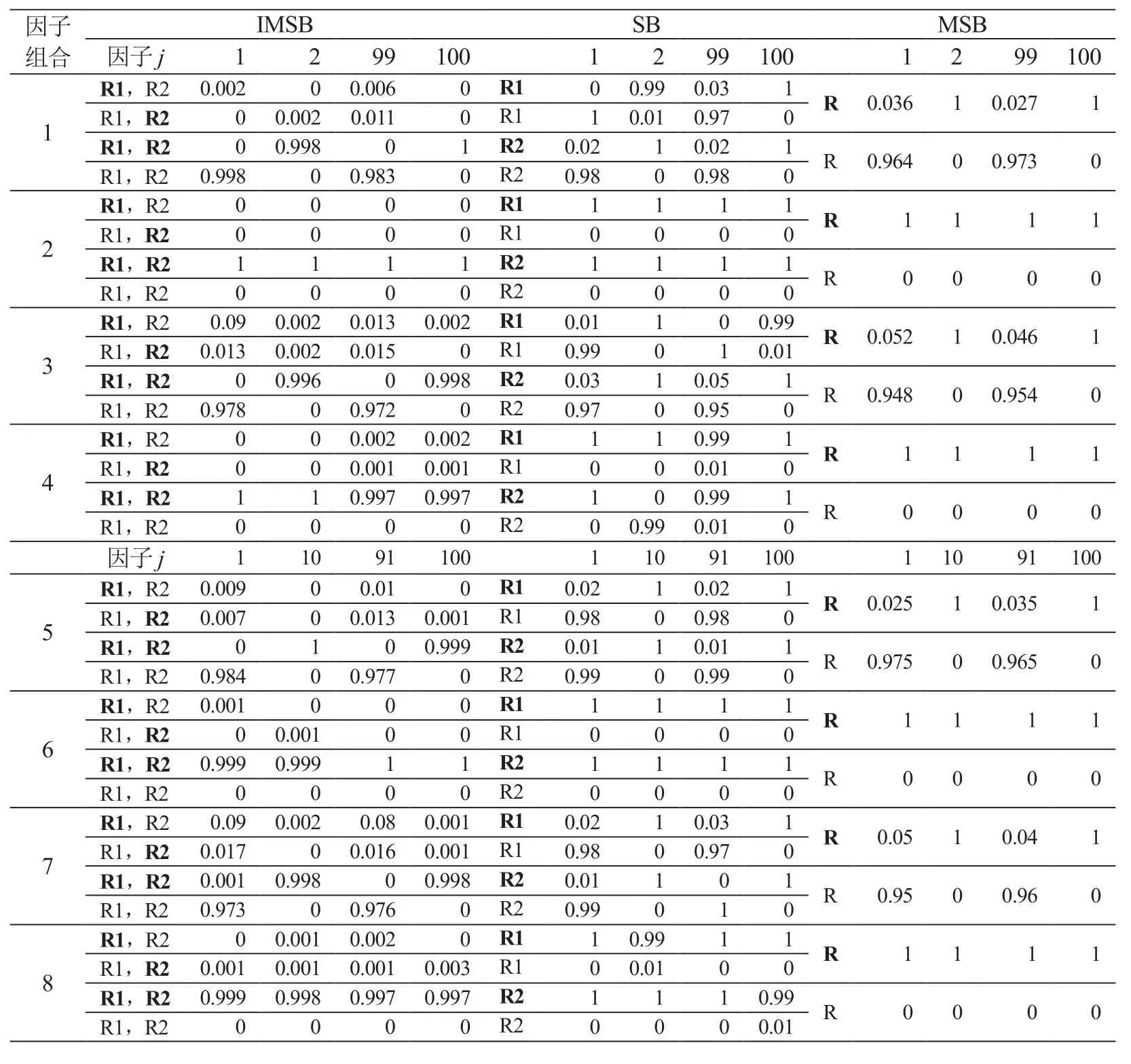
表3　IMSB，MSB法及SB法筛选结果Pr｛DI｝统计效力比较Table 3 Efficacy comparisons among，MSB and SB

因子组合IMSB 　SB 　MSB因子j 　1 　2 　99 　100 　　1 　2 　99 100 　　1 　2 　99 100 R1，R2 　0.002 　0 　0.006 　0 　R1 　0 　0.99 　0.03 　1 　R 　0.036 　1 　0.027 　1 1 R1，R2 　0 　0.002 　0.011 　0 　R1 　1 　0.01 　0.97 　0 R1，R2 　0 　0.998 　0 　1 　R2 　0.02 　1 　0.02 　1 　R 　0.964 　0 　0.973 　0 R1，R2 　0.998 　0 　0.983 　0 　R2 　0.98 　0 　0.98 　0 R1，R2 　0 　0 　0 　0 R1 　1 　1 　1 　1 R 　1 　1 　1 　1 2 R1，R2 　0 　0 　0 　0 R1 　0 　0 　0 　0 R1，R2 　1 　1 　1 　1 R2 　1 　1 　1 　1 R 　0 　0 　0 　0 R1，R2 　0 　0 　0 　0 R2 　0 　0 　0 　0 R1，R2 　0.09 　0.002 　0.013 　0.002 　R1 　0.01 　1 　0 　0.99 　R 　0.052 　1 　0.046 　1 3 R1，R2 　0.013 　0.002 　0.015 　0 　R1 　0.99 　0 　1 　0.01 R1，R2 　0 　0.996 　0 　0.998 　R2 　0.03 　1 　0.05 　1 　R 　0.948 　0 　0.954 　0 R1，R2 　0.978 　0 　0.972 　0 　R2 　0.97 　0 　0.95 　0 R1，R2 　0 　0 　0.002 　0.002 　R1 　1 　1 　0.99 　1 　R 　1 　1 　1 　1 4 R1，R2 　0 　0 　0.001 　0.001 　R1 　0 　0 　0.01 　0 R1，R2 　1 　1 　0.997 　0.997 　R2 　1 　0 　0.99 　1 　R 　0 　0 　0 　0 R1，R2 　0 　0 　0 　0 　R2 　0 　0.99 　0.01 　0因子j 　1 　10 　91 　100 　　1 　10 　91 　100 　　1 　10 　91 　100 R1，R2 　0.009 　0 　0.01 　0 　R1 　0.02 　1 　0.02 　1 　R 　0.025 　1 　0.035 　1 5 R1，R2 　0.007 　0 　0.013 　0.001 　R1 　0.98 　0 　0.98 　0 R1，R2 　0 　1 　0 　0.999 　R2 　0.01 　1 　0.01 　1 　R 　0.975 　0 　0.965 　0 R1，R2 　0.984 　0 　0.977 　0 　R2 　0.99 　0 　0.99 　0 R1，R2 　0.001 　0 　0 　0 R1 　1 　1 　1 　1 　R 　1 　1 　1 　1 6 R1，R2 　0 　0.001 　0 　0 　R1 　0 　0 　0 　0 R1，R2 　0.999 　0.999 　1 　1 　R2 　1 　1 　1 　1 　R 　0 　0 　0 　0 R1，R2 　0 　0 　0 　0 R2 　0 　0 　0 　0 R1，R2 　0.09 　0.002 　0.08 　0.001 　R1 　0.02 　1 　0.03 　1 　R 　0.05 　1 　0.04 　1 7 R1，R2 　0.017 　0 　0.016 　0.001 　R1 　0.98 　0 　0.97 　0 R1，R2 　0.001 　0.998 　0 　0.998 　R2 　0.01 　1 　0 　1 　R 　0.95 　0 　0.96 　0 R1，R2 　0.973 　0 　0.976 　0 　R2 　0.99 　0 　1 　0 R1，R2 　0 　0.001 　0.002 　0 　R1 　1 　0.99 　1 　1 　R 　1 　1 　1 　1 8 R1，R2 　0.001 　0.001 　0.001 　0.003 　R1 　0 　0.01 　0 　0 R1，R2 　0.999 　0.998 　0.997 　0.997 　R2 　1 　1 　1 　0.99 　R 　0 　0 　0 　0 R1，R2 　0 　0 　0 　0 　R2 　0 　0 　0 　0.01

由于SB法无法同时对多个响应的显著性进行判断，故只能逐一对响应1和响应2采用SB法进行分析. R1，R1，R2，R2分别表示因子对响应1显著，不显著，对响应2显著，不显著四种可能的判定结果.例如，对于第1个因子组合中的1号因子而言，R1=1，即SB法最终有1 000次(=1000×1)判定因子1对响应1不显著；R2=0.02，即有20次(=1000×0.02)判定响应2显著；R2=0.98，即有980次(=1000×0.98)判定响应2不显著.

由于MSB法仅能笼统地判定对响应1或响应2是否有显著性效应，故仅用单个字母.例如，对于第1个因子组合中的1号因子而言，R=0.036，即MSB法最终有36次(=1000×0.036)判定1号因子对响应1或2显著；R=0.964，即有964次(=1000×0.964)判定响应1和2都不显著.由该表的值可看出，当Pr｛群组j′-j为重要群组，Pr｛群组j′-j为重要群组 | β(l)，j′-j≥∆1=4｝≥γ=0.90时，三种方法的八个因子组合都保证了筛选实验的统计效力.然而，MSB法无法实现单个因子j对所有响应是否具重要性的判断，而仅能粗略地将两个响应视为一整体做出分析，从而无法获得因子对所有响应影响的重要性信息.相反，IMSB法有效地弥补了这一不足，它能识别出因子对所有响应的效应大小，使决策者可更全面地把握仿真系统运行特征.因此，IMSB深化并拓展了多重响应序贯分支法.

4　结束语

由于仿真系统经常存在较多的实验因子，运用筛选设计识别出少数关键因子显得尤为重要.当所研究系统的响应个数较多时，传统SB法只能通过对不同响应逐个进行筛选设计的方式判定因子对响应的重要性，效率十分低下.本文针对现有多重响应序贯分支(MSB)筛选法无法解决单个因子对所有响应进行显著性检验的不足，对SPRT进行改进并提出多重响应序贯分支法，实现了因子对所有响应的重要性判断.蒙特卡洛仿真显示所提方法在仅增加较少仿真实验次数即可判定因子对所有响应重要性信息，使决策者能更深刻地洞悉系统的动态运作行为.本文虽提出了新的多重序贯分支筛选法，但限于篇幅，蒙特卡洛实验中仅讨论了响应个数为2时的情形，因而研究更多的响应个数是非常值得研究的一个方向.此外，在SPRT过程中，现有方法(SB法，MSB法和IMSB法)仅在每次分支时控制两类错误发生的概率，而并未对一次完整筛选过程的误差概率进行控制，因而今后可参考如De等[24]和Döhler[25]的总体错误推断(familywise error rate)的方法改进SPRT过程.最后，将本文所提方法应用到实际仿真系统也有待研究.

[1]徐超，周宗放.中小企业联保贷款信用行为演化博弈仿真研究.系统工程学报，2014，29(4)：477-486. Xu C，Zhou Z F.The evolutionary game simulation on credit behavior of SMEs’guaranteed loans.Journal of Systems Engineering，2014，29(4)：477-486.(in Chinese)

[2]王潇，王红卫，祁超.基于多Agent强化学习的流水线维护策略.系统工程学报，2013，28(5)：702-708. Wang X，Wnag H W，Qi C.Maintenance policies for flow line based on multi-agent reinforcement learning.Journal of Systems Engineering，2013，28(5)：702-708.(in Chinese)

[3]崔凯楠，郑晓龙，文丁，等.计算实验研究方法及应用.自动化学报，2013，39(8)：1157-1169. Cui K N，Zheng X L，Wen D，et al.Researches and applications of computational experiments.Acta Automatica Sinica，2013，39(8)：1157-1169.(in Chinese)

[4]盛昭瀚，张维.管理科学研究中的计算实验方法.管理科学学报，2011，14(5)：1-10. Sheng Z H，Zhang W.Computational experiments in management science and research.Journal of Management Sciences in China，2011，14(5)：1-10.(in Chinese)

[5]Santner T J，Williams B J，Notz W I.The Design and Analysis of Computer Experiments.New York：Springer Verlag，2003.

[6]Kleijnen J P C.Design and Analysis of Simulation Experiments.New York：Springer US，2008.

[7]Kleijnen J P C，Sanchez S M，Lucas T W，et al.State-of-the-art review：A user’s guide to the brave new world of designing simulation experiments.INFORMS Journal on Computing，2005，17(3)：263-289.

[8]Chen V C P，Tsui K L，Barton R R，et al.A review on design，modeling and applications of computer experiments.IIE Transactions，2006，38(4)：273-291.

[9]Montgomery D C.Design and Analysis of Experiments.6th ed.New York：John Wiley&Sons，2007.

[10]Shi W，Kleijnen J P C，Liu Z X.Factor screening for simulation with multiple responses：Sequential bifurcation.European Journal of Operational Research，2014，237(1)：136-147.

[11]Kleijnen J P C，Bettonvil B W，Persson F.Screening for the Important Factors in Large Discrete-event Simulation Models：Sequential Bifurcation and Its Applications.New York：Springer，2006，287-307.

[12]Wan H，Ankenman B E，Nelson B L.Controlled sequential bifurcation：A new factor-screening method for discrete-event simulation. Operations Research，2006，54(4)：743-755.

[13]Wan H，Ankenman B E，Nelson B L.Improving the efficiency and efficacy of controlled sequential bifurcation for simulation factor screening.INFORMS Journal on Computing，2010，22(3)：482-492.

[14]Shi W，Shang J，Liu Z-X，et al.Optimal design of the auto parts supply chain for JIT operations：Sequential bifurcation factor screening and multi-response surface methodology.European Journal of Operational Research，2014，236(2)：664-676.

[15]Bettonvil B W，Kleijnen J P C.Searching for important factors in simulation models with many factors：Sequential bifurcation. European Journal of Operational Research，1997，96(1)：180-194.

[16]Cheng R C H.Searching for important factors：Sequential bifurcation under uncertainty//Atlanta：Institute of Electrical and Eletronics Engineers，1997：275-280.

[17]Wan H，Ankenman B E.Two-stage controlled fractional factorial screening for simulation experiments.Journal of Quality Technology，2007，39(2)：126-139.

[18]Shen H，Wan H.Controlled sequential factorial design for simulation factor screening.European Journal of Operational Research，2009，198(2)：511-519.

[19]Shen H，Wan H，Sanchez S M.A hybrid method for simulation factor screening.Naval Research Logistics，2010，57(1)：45-57.

[20]Frazier P I，Jedynak B，Chen L.Sequential screening：A Bayesian dynamic programming analysis of optimal group-splitting// Atlanta：Institute of Electrical and Eletronics Engineers，2012：1-12.

[21]Kleijnen J P C.Factor Screening in Simulation Experiments：Review of Sequential Bifurcation.New York：Springer，2009，153-167.

[22]Wu C F J，Hamada M S.Experiments：Planning，Analysis，and Optimization.2th ed.New York：Wiley，2009.

[23]Hartmann M.An improvement on paulson’s procedure for selecting the poprlation with the largest mean from k normal populations with a common unknown variance.Sequential Analysis，1991，10(1)：1-16.

[24]De S K，Baron M.Step-up and step-down methods for testing multiple hypotheses in sequential experiments.Journal of Statistical Planning and Inference，2012，142(7)：2059-2070.

[25]Döhler S.A sufficient criterion for control of some generalized error rates in multiple testing.Statistics&Probability Letters，2014，92(0)：114-120.

IMSB screening method based on improved SPRT

Shi Wen1，2，Leng Kaijun2，Bi Ya2
(1.School of Management，Huazhong University of Science and Technology，Wuhan 430074，China；2.School of Logistics and Engineering Management，Hubei University of Economics，Wuhan 430205，China)

To address the weakness of multi-response sequential bifurcation(MSB)of being incapable of identifying significance of a given factor for all types of response，this paper proposed an improved MSB method，called IMSB for factor screening in discrete-event simulation.This IMSB，by ameliorating Wald’s sequential probability ratio test(SPRT)，can discern any individual factor effect as being important or unimportant for all types of responses with only a small amount of replicates increases and the statistical efficacy is guaranteed.The comparative analysis in Monte Carlo simulation between SB，MSB and IMSB indicates that all these methods give appropriate type-I error rates and powers，and that both MSB and IMSB requires much fewer replicates than SB does.Moreover，unlike MSB，an individual factor effect whether important for a given response is available in IMSB.IMSB can be applied to post-simulation analysis of large-scale simulation，which makes it attractive for a wide variety of simulation applications.

screening；sequential bifurcation；multi-responses；simulation experiments

TP273

A

1000-5781(2016)03-0297-10

10.13383/j.cnki.jse.2016.03.002

施文(1981-)，男，湖北武汉人，博士，副教授，博士，研究方向：仿真优化及物流系统仿真，Email：shi3wen@163.com；

冷凯君(1981-)，男，湖南浏阳人，博士，副教授，研究方向：仿真优化，Email：391627@qq.com；

毕娅(1978-)，女，湖北武汉人，博士，副教授，研究方向：仿真优化，Email：21259537@qq.com.

2014-07-11；

2015-12-29.

国家自然科学基金资助项目(71402048；71372134)；博士后面上基金资助项目项目(2015M582228)；湖北省科技支撑计划软科学研究类资助项目(2014BDF110)；湖北物流发展研究中心资助项目(2015A01).