全支付拍卖的支付规则与期望收益研究

黄　俊，冉茂盛，郑　宇

(1.重庆大学经济与工商管理学院，重庆400030；2.南开大学组合数学中心，天津300071)



全支付拍卖的支付规则与期望收益研究

黄俊1，冉茂盛1，郑宇2

(1.重庆大学经济与工商管理学院，重庆400030；2.南开大学组合数学中心，天津300071)

为探讨全支付拍卖环境下支付规则对拍卖结果的影响，分别基于独立私人价值和关联价值前提，构建了一类广义的全支付拍卖模型，此时赢者支出为最高报价和次高报价的线性凸组合，未获得物品的投标人支付其报价.运用博弈理论，在得出贝叶斯纳什均衡策略及其存在性条件的基础上，分析了支付规则对投标策略及其区间的影响，进一步研究表明：在独立私人价值假设下，收益等价性定理成立，全支付拍卖的期望收益与支付规则无关；在关联价值假设下，收益等价性定理不再成立，拍卖期望收益依赖于支付规则，参数越大期望收益越高.

独立私人价值；关联价值；全支付拍卖；支付规则；期望收益

1　引　言

拍卖的理论研究始于Vickrey[1]，之后Myerson[2]和Riley等[3]基于独立私人价值(IPV)假设得出了著名的收益等价性定理.然而现实中，竞标人对物品的价值并不总是相互独立的.因此，Milgrom等[4]首先引入关联价值(AV)假设，对4种标准拍卖方式的期望收益进行比较，此时收益等价性定理不再成立，进一步得出了“连接原理”(linkage principle)：如果有更多的关联信息被连接到赢者的付价，那么卖者的期望收益会更高.此后，大量文献基于关联价值假设对各种拍卖形式的投标策略、期望收益、拍卖效率等进行讨论和拓展[57].

关于期望收益的比较，早期拍卖理论主要关注具有“有条件承诺”特性的拍卖形式，即只有满足某种条件(赢得拍卖)时投标人才会支付价格，又称为赢者支付拍卖，例如英式、荷式、一级价格和二级价格等拍卖形式.而在经济社会生活中广泛存在着类似于“无条件承诺”特性的拍卖，此时投标人无条件向卖者支付价格，即全支付拍卖，又称竞赛.全支付拍卖最早出现在理论生物学的研究文献中[8]，其典型形式为全支付一级价格和二级价格拍卖(又称消耗战).在此拍卖形式下，乔恒等[9]基于独立私人价值(IPV)假设，对全支付一级价格拍卖和全支付二级价格拍卖的均衡投标策略和期望收益进行比较，得出了收益等价性定理.

为了研究拍卖支付规则对期望收益的影响，有必要引入λ-拍卖.其本质上是一种采用支付规则参数依赖的广义密封拍卖，参数λ为拍卖的支付规则.最早由Güth等[10]提出，在独立私人价值的赢者支付(winner-pay)λ-拍卖中，他们证明了支付规则影响投标人的均衡策略，但不影响拍卖的期望收益，即收益等价性定理依然成立.同样基于独立私人价值和赢者支付前提，Plum[11]研究了两个投标人分布函数非对称的赢者支付λ-拍卖中非对称均衡投标策略的存在性和唯一性.而在全支付λ-拍卖中，赢者支出仍为最高报价和次高报价的线性凸组合，但未获得物品的投标人也要支付其报价给卖者.在这方面的理论研究较少，只有Amann等[12]基于独立私人价值假设，在非对称的全支付λ-拍卖模型中研究了非对称的均衡投标策略的存在性和唯一性.此外，这一方法也被拓展到双方叫价拍卖(double auction)中，此时参数λ被理解为买卖双方议价的能力[1315].

现有文献大多都是基于独立私人价值前提下研究赢者支付的λ-拍卖[10，11]，包括投标人的均衡投标策略和拍卖期望收益及其与拍卖规则的关系，而关于全支付拍卖模型的研究较少.虽然Amann等[12]采用的模型与本文独立私人价值模型部分类似，但其只分析了非对称投标人的均衡策略，未见在全支付拍卖模型中关于支付规则对均衡投标策略及拍卖期望收益影响的系统研究.在现实中，全支付拍卖这种“无条件承诺”的拍卖类型被广泛用于分析包含冲突和竞争的经济社会问题，例如寻租行为[16]，专利和科技竞赛[17]以及军备竞赛[18]等问题，因而对其均衡策略和期望收益进行研究有着现实的经济意义.全支付λ-拍卖作为一类广义的全支付拍卖，将全支付一级价格和全支付二级价格拍卖这两种拍卖形式置于统一的分析框架下.一方面，从机制设计的角度，有助于分析私人信息与最终支出的连接对拍卖收益的影响，并为实践活动提供更好的理论指导.另一方面，该类拍卖又可理解为不完美信息下的全支付拍卖，因此被广泛用于不确定环境中投标人均衡策略的分析[19].

为此本文分别基于独立私人价值前提和关联价值前提，研究了全支付λ-拍卖中的投标人均衡策略及其区间，并分析了支付规则对卖者期望收益的影响.

2　全支付拍卖模型

假定卖者有1个不可分割的物品通过拍卖出售，有n个潜在购买者.用Xi表示投标人i对物品价值拥有的私人信息.用Vi表示投标人i对物品的最终消费价值.

根据Amann等[12]，用如下规则来定义λ-全支付拍卖：n个投标人同时报价，物品由出价最高的投标人获得.投标人i的出价为bi，其支付(payoff)为

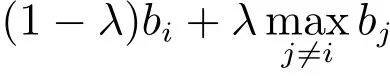
在λ-拍卖中，用β(x，λ)表示具有私人信息x的投标人的对称均衡投标策略.假设具有私人信息x的投标人的出价为b，则当b=β(x，λ)时投标人的期望收益最大，即

3　全支付独立私人价值模型

在IPV模型中，投标人对物品的最终消费价值为其私人信息，即Vi=Xi.假设投标人的私人信息在区间[0，a]上独立同分布，其分布函数F(·)及相应密度函数在(0，a)上连续可微且为正.

根据式(1)，私人信息为x=v的投标人的出价为b，从而有

其中λ0是常数，，相应的为其密度函数.

当b=β(x，λ)时，上式最大，于是有

下面给出拍卖的均衡投标策略.

定理1在独立私人价值模型中，给定边界条件β(0，λ)=0，全支付λ-拍卖的均衡投标策略为

证明先证必要性.由式(2)并结合边界条件β(0，λ)=0，可得均衡投标策略β(x，λ)，即式(3)所示.再证充分性.因为私人信息为x的投标人的出价为β(z，λ)时的期望收益为

其中βy表示β(y，λ)对y的一阶偏导数.

由于对所有x＞y，有(x-y)g(y)＞0，对所有x＜y，有(x-y)g(y)＜0，故E[Wi(β(z，λ)，x)]在z= x时取最大值，即满足激励相容(IC)条件.同时

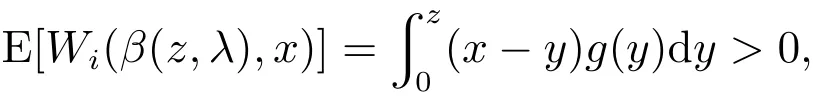
投标者选择参与拍卖，即满足个体理性(IR)条件.

推论1在独立私人价值模型中，支付规则λ越大，投标人的报价越“积极”.即对所有x∈(0，a)，如果λ1＜λ2，则β(x，λ1)＜β(x，λ2)成立.

定理2在独立私人价值模型中，若支付规则λ∈[0，1)，则均衡策略有上界且

证明若支付规则λ=0，可得

若λ∈(0，1)，则有

由定理2可以看出，在λ∈[0，1)时，投标人的均衡投标策略均有界；而当λ=1时，即全支付二级价格拍卖的均衡投标策略无上界.在对投标人的均衡策略及其区间进行分析的基础上，再比较卖者在λ-拍卖中的期望收益.

定理3在独立私人价值模型中，全支付λ-拍卖中的卖者期望收益与支付规则无关，即对所有支付规则λ∈[0，1]，拍卖的卖者期望收益相等.

证明用e(x)表示拥有私人信息x的投标人的期望支出，于是

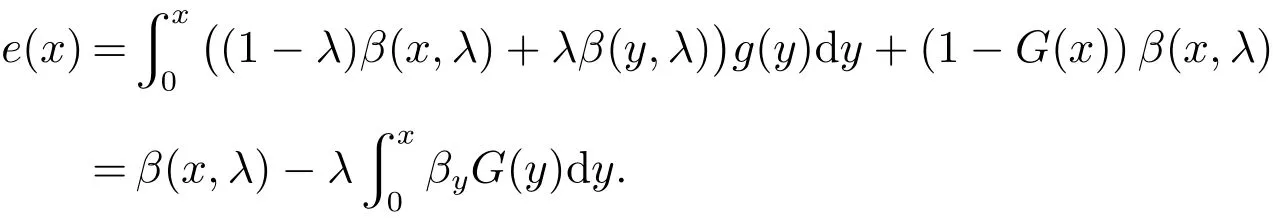
将式(2)和式(3)代入上式，得

也就是说，投标人的期望支出与支付规则无关，从而拍卖产生的期望收益相等. 证毕

从上述定理可以看出，虽然均衡投标策略随着支付规则λ的增大而增大，但一类广义全支付拍卖产生的期望收益依然相等，收益等价性定理在λ∈[0，1]上成立.从信息关联角度解释，尽管λ-拍卖在赢者支出与次高报价之间建立了连接(linkage)，但由于IPV模型中私人信息独立的假设意味着最终支付与次高价的连接不会影响投标人对物品的估价，所以投标人期望支出不变，从而拍卖产生的期望收益不变.因此，结论意味着卖者设置的支付规则不会改变拍卖的结果及其期望收益，进而在IPV环境的拍卖实践中卖者不必过于关心拍卖所采取的形式.如果将此类拍卖理解为不完美信息下的拍卖，那么结论意味着投标人所处拍卖环境的不确定性不会对拍卖的期望收益产生影响.同时，乔恒等[9]证明了全支付一级价格拍卖(λ=0)和全支付二级价格拍卖(λ=1)的收益等价性，定理3是其结论在λ∈[0，1]整个区间上的推广和一般化.实际上，同样可以证得全支付λ-拍卖产生的期望收益也等于赢者支付λ-拍卖的期望收益.

4　全支付关联价值模型

该模型描述了对物品的价值和私人信息分布这两种相关性：1)投标人对物品的最终消费价值不仅取决于自己的私人信息，也取决于其他投标人对物品的私人信息；2)所有竞标者对物品的估价有正相关性，体现在分布函数上，当一个投标人私人信息较高时，其他投标人私人信息也高的概率更大.用X= (X1，X2，...，Xn)表示n个投标人在区间[0，a]上的私人信息(或信号)向量.用S=(S1，S2，...，Sm)表示其他影响物品价值，但不能被投标人所观察到的随机变量，而S中的某些变量可能被卖者所观察到，则物品对投标人的最终价值为

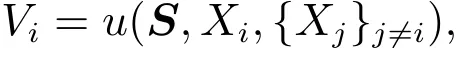
其中u是非负、连续的且关于各变量严格递增，同时满足E[Vi]＜∞.

随机变量S1，S2，...，Sm，X1，X2，...，Xn的联合密度函数f(S，X1，X2，...，Xn)满足所谓的“关联性质”，即对所有z和z′有

其中z∨z′=(max｛z，z′｝)为向量z和z′各分量最大部分组成的向量；z∧z′=(min｛z，z′｝)为向量z 和z′各分量最小部分组成的向量.

根据式(1)，给定Xi=x时，报价为b的投标人期望支付(payoff)为

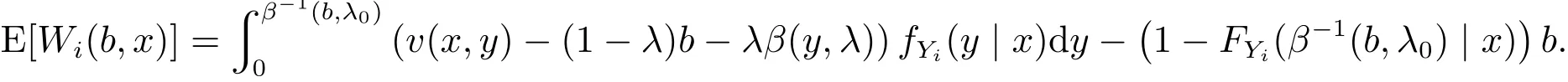
选择合适的b以最大化投标者的期望支付，此时b=β(x，λ)，β(x，λ)对x的一阶偏导数

于是，给出均衡策略β(x，λ).为了验证充分性，为此有必要增加约束条件.

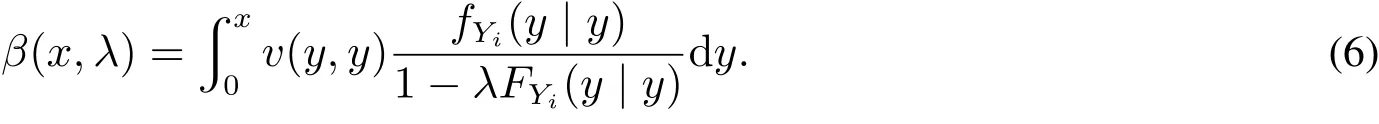
证明先证必要性.由式(5)并结合边界条件β(0，λ)=0，可得均衡投标策略β(x，λ)，即式(6)所示.再证充分性.私人信息为x的投标人的出价为β(z，λ)时的期望收益为

将式(5)和式(6)代入上式，得

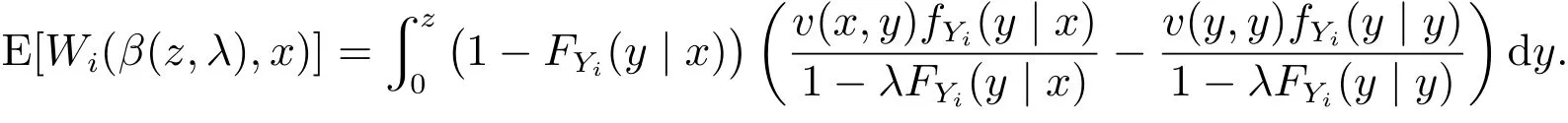
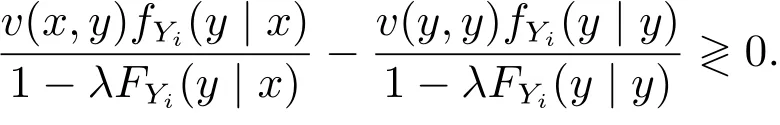
因而E[Wi(β(z，λ)，x)]在z=x时取最大值，即满足激励相容(IC)条件，此时

投标者选择参与拍卖，即满足个体理性(IR)条件.

推论2在关联价值模型中，支付规则λ越大，投标人的报价同样越“积极”，即对所有x∈(0，a)，如果λ1＜λ2，则β(x，λ1)＜β(x，λ2)成立.

以上推论可由式(6)和定理4直接得出，与推论1类似，投标人的均衡策略也取决于拍卖的支付规则.特别的，全支付一级价格拍卖和二级价格拍卖的均衡策略分别为

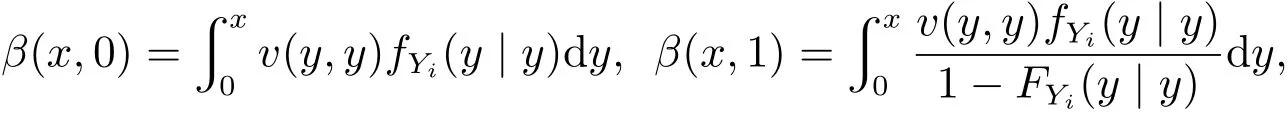
此时全支付二级价格拍卖的投标策略同样比全支付一级价格拍卖更积极，即β(x，0)＜β(x，1).若给定支付规则，此时投标人策略区间上限的性质如下.

进一步，若λ=0，可得

由定理5可知，当投标人的私人信息趋向于上限(x→a)时，即使物品的最终价值v(a，a)是有限的，全支付二级价格拍卖(λ=1)的均衡投标策略依然无上界.在对投标人的均衡策略及其区间进行分析的基础上，再比较卖者在λ-拍卖中的期望收益.

证明用e(x，λ)表示λ-拍卖中拥有私人信息x的投标人的期望支出，于是

将式(5)和式(6)代入上式，得到

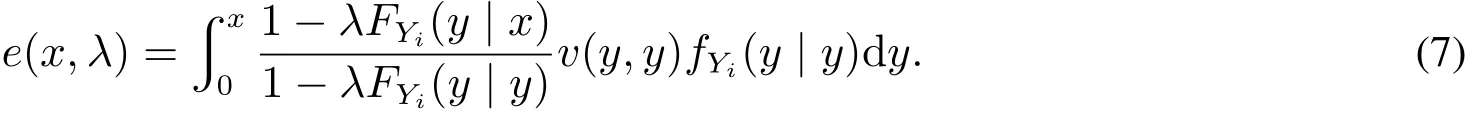
则对所有的λ1，λ2∈[0，1]且λ1＜λ2有

而由于FYi(y|x)关于x单调递减，可知对所有y＜x有FYi(y|y)＞FYi(y|x).再由上式可得

所以，对所有λ1＜λ2，有e(x，λ1)＜e(x，λ2)，从而支付规则λ越大，拍卖的期望收益越高.证毕.

由定理6可以看出，与独立私人价值情形不同，关联价值前提下收益等价性定理不再成立，拍卖产生的期望收益依赖于支付规则.支付规则参数λ越大，拍卖的期望收益越高.从信息关联角度解释，λ-拍卖在投标人支出与次高报价之间建立了连接(linkage)，在关联价值假设下，投标人对物品私人信息较高往往意味着其他投标人的私人信息也较高，从而次高报价就较高，这样投标人对物品的私人信息通过支付规则影响其最终支付.所以，投标人对物品的私人信息传导到次高报价的程度越充分(即λ越大)，投标人的期望支出进而拍卖的期望收益越高.与经典理论中的连接原理(linkage principle)[4]强调新增信息的作用不同，上述定理突出了既有信息前提下的信息向下关联程度对卖方期望收益的影响，从而对连接原理进行了理论扩展，发现既有信息的向下关联程度越高卖方期望收益越高.从不完美信息角度，定理也可理解为在投标人面对的不确定拍卖环境中，拍卖为全支付二级价格拍卖的概率越大，则拍卖的期望收益越高.

特别地，作为全支付λ-拍卖的极端形式，当λ=0和λ=1时定理同样成立，也就是说全支付一级价格拍卖产生的期望收益大于全支付二级价格拍卖(消耗战)所产生的期望收益，即e(x，0)＜e(x，1).

5　数值分析

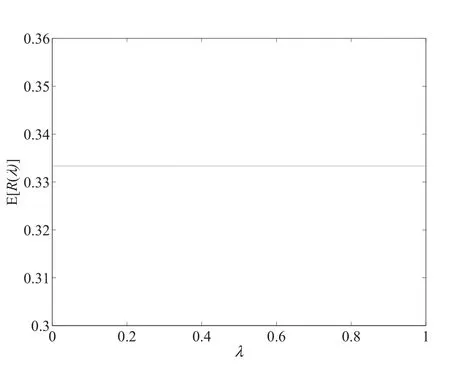
图2　在IPV模型中，支付规则对期望收益的影响Fig.2 The effect of pricing rule λ on seller’s expected revenue in IPV model

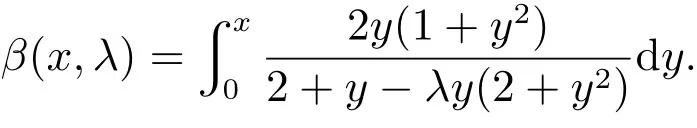
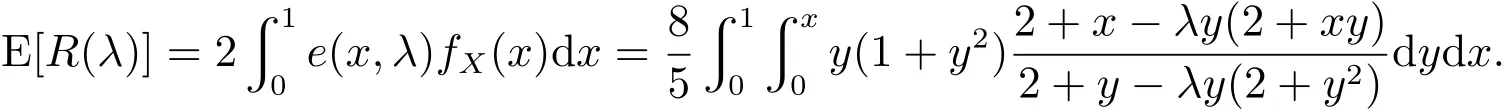
支付规则参数λ对卖方期望收益的影响如图4所示，可以看出AV前提下拍卖的期望收益随参数λ单调递增，即为定理6的结论.

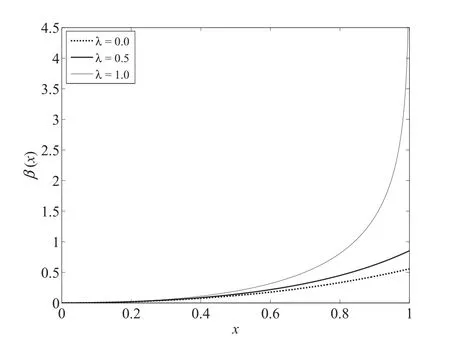
图3　在AV模型中，当λ分别为0，0.5和1时的投标策略Fig.3 The bidding strategies for pricing rule λ equals 0，0.5 and 1 in AV model

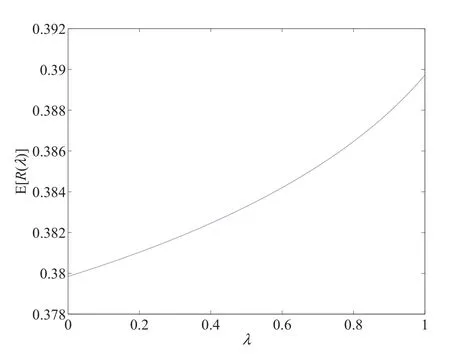
图4　在AV模型中，支付规则对期望收益的影响Fig.4 The effect of pricing rule λ on seller’s expected revenue in AV model

6　结束语

本文分别基于独立私人价值和关联价值的λ-拍卖模型研究了全支付拍卖的支付规则对投标人均衡策略和卖者期望收益的影响.在独立私人价值假设下，根据期望收益最大化目标，推出投标人的贝叶斯纳什均衡投标策略，并发现：虽然投标人的均衡报价随支付规则λ而递增，但支付规则对卖者的期望收益没有影响，收益等价性定理成立.然后，在关联价值假设下，给出对称贝叶斯纳什均衡策略存在的充分条件，并得出均衡策略的解析解.此时，收益等价性定理不再成立，卖者的期望收益依赖于支付规则.支付规则λ越大，拍卖的期望收益越高，当拍卖为全支付二级价格拍卖(消耗战)时，期望收益达到最大.不同于连接原理所强调的新增信息对卖方收益的影响，本文的结论强调既有信息的向下(次高报价)关联程度越高卖方期望收益越高.此外，还对投标人均衡策略的区间进行了分析.本文假设不存在预算约束，未来可以对包含预算约束的模型进行研究，分析预算约束对投标人策略及卖者收益的影响；另外，卖方所拥有信息的披露政策对卖方收益的影响也是一个值得研究的课题[21].

[1]Vickrey W.Counterspeculation，auctions，and competitive sealed tenders.Journal of Finance，1961，16(1)：8-37.

[2]Myerson R.Optimal auction design.Mathematics of Operations Research，1981，6(1)：58-73.

[3]Riley J，Samuelson W.Optimal auction.American Economic Review，1981，71(3)：381-392.

[4]Milgrom P，Weber R.A theory of auctions and competitive bidding.Econometrica，1982，50(4)：1089-1122.

[5]Fang H，Parreiras S.Equilibrium of affiliated value second price auctions with financially constrained bidders：The two-bidder case. Games and Economic Behavior，2002，39(2)：215-236.

[6]Kotowski M，Li F.On the continuous equilibria of affiliated-value，all-pay auctions with private budget constraints.Games and Economic Behavior，2014，85(1)：84-108.

[7]Siegel R.Asymmetric all-pay auctions with interdependent valuations.Journal of Economic Theory，2014，153(1)：684-702.

[8]Maynard S.The theory of games and the evolution of animal conflicts.Journal of Theoretical Biology，1974，47(1)：209-221.

[9]乔恒，邱菀华.两类拍卖的收益等价性和均衡投标价格排序.中国管理科学，2005，13(10)：224-227. Qiao H，Qiu W H.Revenue equivalence and equilibrium bidding rank of two kinds of auctions.Chinese Journal of Management Science，2005，13(10)：224-227.(in Chinese)

[10]Güth W，Damme E.A comparison of pricing rules for auctions and fair division games.Social Choice and Welfare，1986，3(3)：177-198.

[11]Plum M.Characterization and computation of nash-equilibria for auctions with incomplete information.International Journal of Game Theory，1992，20(4)：393-418.

[12]Amann E，Leininger W.Asymmetric all-pay auctions with incomplete information：The two-player case.Games and Economic Behavior，1996，14(1)：1-18.

[13]Satterthwaite M，Williams S.The optimality of a simple market mechanism.Econometrica，2002，70(5)：1841-1863.

[14]李长杰，王先甲，范文涛.水权交易机制及博弈模型研究.系统工程理论与实践，2007，27(5)：90-94，100. Li C J，Wang X J，Fan W T.Design of mechanism and bayesian model of water rights market.Systems Engineering：Theory and Practice，2007，27(5)：90-94.(in Chinese)

[15]Wasser C.Bilateral k+1-price auctions with asymmetric shares and values.Games and Economic Behavior，2013，82(1)：350-368.

[16]Baye M，Kovenock D，Vries C.Rigging the lobbying process：An application of the all-pay auction.American Economic Review，1993，83(1)：289-294.

[17]Leininger W.Patent competition，rent dissipation and the persistence of monopoly.Journal of Economic Theory，1991，53(1)：146-172.

[18]Leininger W.Escalation and cooperation in conflict situations-the dollar auction revisited.Journal of Conflict Resolution，1989，33(1)：231-254.

[19]Straume D.Rent-seeking in a unionised monopoly.Economics of Governance，2002，3(2)：117-134.

[20]Riley J.Asymmetric Rontests.Los Angeles：University of California，1991.

[21]洪宗友，汪定伟.多属性招标拍卖中买卖双方的最优策略研究.系统工程学报，2014，29(4)：458-467. Hong Z Y，Wang D W.Optimal strategies of auctioneer and bidders in multi-attribute procurement auctions.Journal of Systems Engineering，2014，29(4)：458-467.(in Chinese)

Research on pricing rules and expected revenue under all-pay auctions

Huang Jun1，Ran Maosheng1，Zheng Yu2
(1.School of Economics and Business administration，Chongqing University，Chongqing 400030，China；2.Center for Combinatorics，Nankai University，Tianjin 300071，China)

In order to study the influence of pricing rules on auction outcomes，this paper examines a large class of all-pay auctions within the independent private values(IPV)paradigm and the affiliated values(AV) paradigm，respectively.The explicit solutions of symmetric Bayesian-Nash equilibrium bidding strategies in all-pay auctions are determined.From the seller’s perspective，if the bidders’types are independently distributed，the seller is indifferent between the auctions with the whole continuum of pricing rules，thus the revenue-equivalence theorem holds.Given a sufficient condition for the existence of an equilibrium，the seller’s preference is biased from the theorem if bidders’types are affiliated：the seller then prefers auctions with higher parameters of pricing rules.That is，the seller’s expected revenue depends on the pricing rules.

independent private values；affiliated values；all-pay auctions；pricing rules；expected revenue

F016

A

1000-5781(2016)03-0328-10

10.13383/j.cnki.jse.2016.03.005

黄俊(1987-)，男，江苏盐城人，博士生，研究方向：拍卖理论，最优机制设计，Email：huangjun@cqu.edu.cn；

冉茂盛(1963-)，男，重庆云阳人，博士，教授，研究方向：拍卖理论，金融经济，投融资理论，Email：ranmaosheng@cqu.edu.cn；

郑宇(1989-)，男，河南光山人，博士生，研究方向：组合数学，拍卖理论，Email：antid@126.com.

2014-07-20；

2015-12-20.

国家自然科学基金资助项目(71071171).