一类含有随机参数的混沌系统的Hopf分岔研究

殷　俊，张建刚，南　娟，卢加荣，庞　琴

(兰州交通大学数理学院， 甘肃　兰州　730070)



一类含有随机参数的混沌系统的Hopf分岔研究

殷俊，张建刚，南娟，卢加荣，庞琴

(兰州交通大学数理学院， 甘肃兰州730070)

文章选取随机变量为系统的随机变量研究含有随机参数混沌系统的Hopf分岔，利用Chebyshev正交多项式逼近理论将含有随机变量的系统转化为等价的确定性系统，通过Hopf分岔定理和Lyapunov系数讨论了随机参数系统的Hopf分岔及稳定性，发现随机系统的渐进稳定性参数区间大小不仅和确定性参数有关，还与随机参数有非常密切的关系.

随机Hopf分岔；Chebyshev正交多项式逼近；稳定性

混沌广泛存在于自然科学各领域中，如数学、生物学、量子力学等领域. 从第一个混沌吸引子被发现后，新的混沌系统不断被人们发现[1-6].为便于控制混沌系统的敏感性和不可预测性，很多同步和控制方法被提出.如脉冲控制法、OGY方法、被动控制法、主动控制法、非线性反馈法、线性状态反馈控制法等．混沌控制在很多领域有广阔的应用前景.由于此方面的研究还停留在定性阶段，对选取模型的准确性和精度要求较高，所以分析含有随机参数的混沌系统尤为关键.目前，处理含有随机参数的随机系统的方法大致包括3类：Monte Carlo 方法[7]、随机有限元方法[8-9]和正交多项式逼近法[10].其中，正交多项式逼近相对于其他两类方法具有较小的局限性，因此被广泛应用[11-16].本文选取参考文献[17]中改进后的模型，在考虑系统不确定性和外界干扰的情况下，提出一个新的含有随机参数的混沌系统，分析新系统的基本稳定性和分岔.

1　随机函数的正交分解基本理论

选取(服从拱形分布)随机变量为系统随机参数进行分析.服从拱形分布的随机变量概率密度函数可表示为[18]：

(1)

相应的第二类Chebyshev多项式的一般表达式为：

(2)

其循环递推公式为：

(3)

其加权正交性可以表示为：

(4)

2　含有随机参数的混沌系统的正交多项式逼近

(5)

(6)

运用正交多项式逼近，响应如下：

(7)

(8)

将任意两个Chebyshev多项式的乘积都转化为它们的线性组合，则(8)式中的非线性项可以简化，并运用Chebyshev多项式的循环递推公式，方程式可以简化后得到：

通过正交多项式逼近得到与之等价的确定性混沌系统，在系统转化过程中对方程关于ζ求期望，所以得到的新的系统是含有随机参数的混沌系统的加权均值系统.

3　随机Hopf分岔分析

3.1Hopf分岔的存在性

通过MAPLE,我们能够得到特征方程：

f(λ)=a0λ6+a1λ5+a2λ4+a3λ3+a4λ2+

a5λ1+a6

其中：

a0=1

a1=2c+2a-2

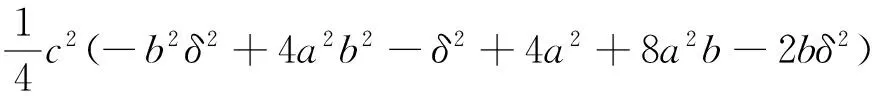
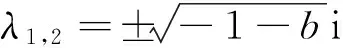
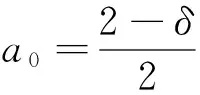
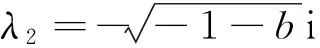
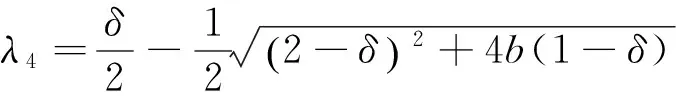
λ5=-c，λ6=-c.

6c2δ+8b2c2-b2c2δ-6b-bδ2+

bδ3+5bδ-4cδ-4b3-8b2-10b+

根据Hopf分岔理论，a0是Hopf分岔临值，若满足a>1且δ>1，当参数a穿过它的临界值a0时，系统在其平衡点O(0,0,0,0,0,0)发生Hopf分岔.

3.2稳定性

在本节中，通过掌握Lyapunov系数对Hopf分岔进行进一步的调查和研究.

x,y

x,x=0.

考虑非线性动力系统

x=f(x,v)(x∈Rn),

v∈Rn为分岔参数，当v=vc时，等式有平衡点x=x0，则等式的右边可表示为:

F(x)=Jx+N(x)

令Cn为在复数域C上定义的一个线性空间，令q∈Cn为一个复合特征向量，满足λ1和p∈Cn为一个伴随特征向量满足以下内容：

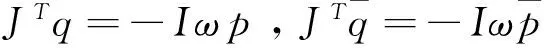
p,q.

当x=(x0,y0,x1,y1,x2,y2)时，B(x,y)和C(x,y，z)分别是双线和三线函数，可以表示为：

i=1,2,…,n

i=1,2,…,n

第一Lyapunov系数被定义为：

我们可以定义系数：

G20=p,B(q,q)，

G11=，

G02=，

G21=-2+

+

通过计算知第一Lyapunov系数为：

其中：A=-c+bc+cδ2-2cδ+b2cδ2+2bcδ2+b2c-4bcδ-

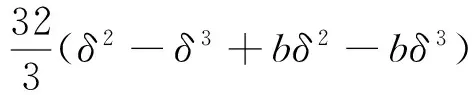
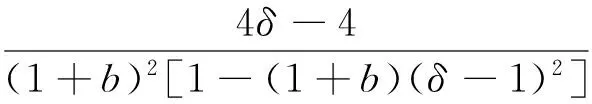
C=-4b+4δ2+8bδ2-16c-8bc-4b2+8cδ2+

8bcδ2+4b2δ2+4δ+16cδ+4bδ，

D=-8c+2δ2+2δ+16cδ+2bδ-2b

4　结论

本文运用Chebyshev正交多项式逼近法分析新的混沌系统的稳定性及Hopf分岔行为. 这个方法将随机系统转化为一个与之等价的确定性系统，然后对其确定性系统通过一个Lyapunov系数法进行分岔分析.结果表明，随机Hopf分岔在新的混沌系统中不仅和传统的Hopf分岔相似，而且还具有一些特性.例如，随机Hopf分岔行为是由于随机参数的强度导致的.本文提出的新的混沌系统的随机分岔的稳定性是不发生改变的.随机因素对系统及其稳定性和Hopf分岔的影响较为显著.随着随机参数强度不断减小，含有随机参数混沌系统的零解渐进稳定的区域逐渐增大.因此，在随机参数系统中我们应当更好地控制参数强度.

[1]FRANCOISM,DENISR,CATHERINEC.Time-varyingtorsionalstiffnessidentificationonaverticalbeamusingChebyshevpolynomials[J].MechanicalSystemsandSignalProcessing, 2015(54)：481-490.

[2]LILP,HUANGLH.ConcurrenthomoclinicbifurcationandHopfbifurcationforaclassofplanarFilippovsystems[J].Math.Anal.Appl, 2014, 411: 83-94.

[3]ISAACA.OntheperiodicorbitbifurcatingfromazeroHopfbifurcationinsystemswithtwoslowandonefastvariables[J].AppliedMathematicsandComputation, 2014, 232: 84-90.

[4]BALANOVZ,HUQW,KRAWCEWICZW.GlobalHopfbifurcationofdifferentialequationswiththresholdtypestate-dependentdelay[J].DifferentialEquations, 2014, 257: 2622-2670.

[5]WANGXD,DENGLW,ZHANGWL.HopfbifurcationanalysisandamplitudecontrolofthemodifiedLorenzsystem[J].AppliedMathematicsandComputation, 2013, 225: 333-344.

[6]DENGLW,WANGXD,PENGM.Hopfbifurcationanalysisforaratio-dependentpredator-preysystemwithtwodelaysandstagestructureforthepredator[J].AppliedMathematicsandComputation,2014,231:214-230.

[7]SHINOZUKAM.Probabilitymodelingofconcretestructures[J].EngMechDivASCE,1972,98:1433-1451.

[8]KLEIBERANDM,HIENTD.TheStochasticFiniteElementMethod:BasicPerturbationTechniqueandComputerImplementation[M].NewYork:WileyPress,1992.

[9]PETTITCL,BERANPS.SpectralandmultiresolutionWienerexpansionsofoscillatorystochasticprocesses[J].SoundVib, 2006, 294: 752-779.

[10]GHAMEMR,SPANSP.Stochasticfiniteelement:Aspectralapproach[M].Berlin:Springer, 1991.

[11]WANXL,KARNIADAKISGE.Anadaptivemulti-elementgeneralizedpolynomialchaosmethodforstochasticdifferentialequations[J].ComputPhys, 2005, 209: 617-642.

[12]FANGT,LENGXL,SONGCQ.Chebyshevpolynomialapproximationfordynamicalresponseproblemofrandomsystem[J].SoundVib,2003,226:198-206.

[13]LENGXL,WUCL,MAXP,etal.BifurcationandchaosanalysisofstochasticDuffingsystemunderharmonicexcitations[J].NonlinearDyn, 2005,42:185-198.

[14]MASJ,XUW,LIW,etal.AnalysisofstochasticbifurcationandchaosinstochasticDuffing-vanderPolsystemviaChebyshevpolynomialapproximation[J].ChinPhys, 2006,15:1231-1238.

[15]WUCL,LEIYM,FANGT.StochasticchaosinaDuffingoscillatoranditscontrol[J].ChaosSolitonsFractals,2006,27:459-469.

[16]MASJ.ThestochasticHopfbifurcationinBrusselatorsystemwithrandomparameter[J]. 2012,219(1):306-319.

[17]MASJ,XUW,FANGT.Analysisofperiod-doublingbifurcationindouble-wellstochasticDuffingsystemviaLaguerrepolynomialapproximation[J].NonlinearDyn, 2008,42:185-196.

[18]蔡国梁，谭振梅，周维怀，等.一个新的混沌系统的动力学分析及混沌控制[J].物理学报，2007，56(11)：6230-6237.

[19]张莹. 非线性随机参数系统的动力学与控制研究[D]. 西安：西北工业大学,2007.

[20]丁双安. 随机参数Duffing-VanDerPol系统在参数激励作用下的非线性动力学行为[D]. 上海：东华大学,2013.

(责任编辑穆刚)

Hopf bifurcation study of a class of chaotic systems containing random parameter

YIN Jun, ZHANG Jiangang, NAN Juan,LU Jiarong，PANG Qin

(Department of Mathematics, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China)

In the paper the random parameter was used to study the Hopf bifurcation of chaotic system containing random parameter, and the Chebyshev polynomial approximation theory was used to change the system containing random parameter into the deterministic equivalent system. Through the Hopf bifurcation theory and Lyapunov coefficient to discuss the Hopf bifurcation and stability of random stochastic parameter system, it shows that the critical value of stochastic Hopf bifurcation is determined not only by deterministic parameters in stochastic system, but also by the intensity of random parameter.

random Hopf bifurcation; Chebyshev polynomial approximation; stability

2016-03-02

殷俊(1991—)，女，甘肃酒泉人，硕士，主要从事概率论与数理统计方面的研究.

O21

A

1673-8004(2016)05-0029-05