一个新混沌纠缠系统的Hopf分岔分析
2016-10-10KutorziEdwinYao张建刚
Kutorzi Edwin Yao, 张建刚, 秦 爽
(兰州交通大学数理学院, 甘肃 兰州 730070)
一个新混沌纠缠系统的Hopf分岔分析
Kutorzi Edwin Yao, 张建刚, 秦爽
(兰州交通大学数理学院, 甘肃兰州730070)
文章基于混沌纠缠方法构造了一个新的混沌系统,通过理论和数值分析验证了该系统存在混沌吸引子.此外,利用非线性动力学理论分析了该系统平衡点的稳定性以及Hopf分岔的存在性和稳定性.经过计算系统在平衡点的第一Lyapunov系数判断Hopf分岔的方向及其稳定性,最后进行数值仿真验证理论分析的正确性.
混沌纠缠;稳定性;Lyapunov系数;Hopf分岔
近年来,人为构造混沌系统已经成为研究热点.混沌的研究开始于1963年,当时洛伦兹对一个天气预报数学模型进行研究[1].该模型表示即便是详细的大气模型也不能做相对长期的天气预测,而当时人们只能预测一个星期的天气[2].混沌通常被定义为一个相对来说比较庞大的非线性现象,它与缺席微观量子领域以及经典物理学的关系非常密切.最近几年,许多学者热衷于对人工混沌系统的设计和构造,并且已经成为一个重要的研究领域[3-7].文献[8]给出了一种被称为混沌纠缠的新的构造混沌的研究方法.这个方法的基本理论是运用纠缠函数的方式纠缠两个或多个稳定的线性子系统并且使其产生出一个人为构成的新混沌系统.混沌纠缠这种方法利用一种更为方便的手段构造并产生新的混沌吸引子.我们完全可以运用混沌纠缠的方法更加简单地构建出一类新的混沌系统. 学者们近几年在认识和研究混沌现象时,发现并构建了许多种混沌系统,许多人专注于这些混沌系统动力学特征的研究[9-10].本文运用混沌纠缠的方法重新构建一个新的超混沌系统,并运用理论推导和数值仿真的方式对该系统存在混沌吸引子的结论做了进一步验证,同时对此系统的动力学行为进行了分析.
1 新混沌系统的构造
考虑两个线性的子系统

(1)
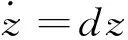
(2)
其中(x,y,z)为状态变量.当a<0,c<0并且d<0时,显然两个子系统是稳定的.经过正弦函数纠缠 (1) 与 (2) 两个线性子系统将会得出以下混沌系统
(3)
其中a<0,c<0,d<0,(b,b1,d1,e)∈R4,纠缠函数为(sinx,siny,sinz).当a=-2,b=6,c=3,d=-4,e=20,d1=40,b1=38时,系统(3)存在一个如图1所示的混沌吸引子.

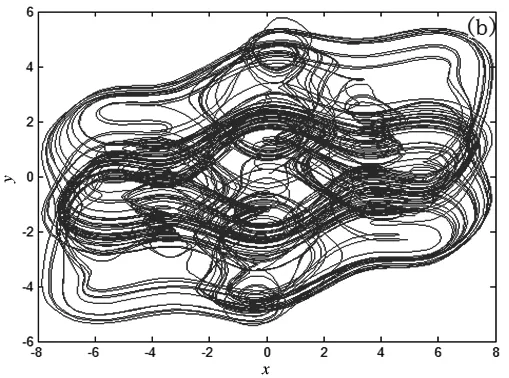
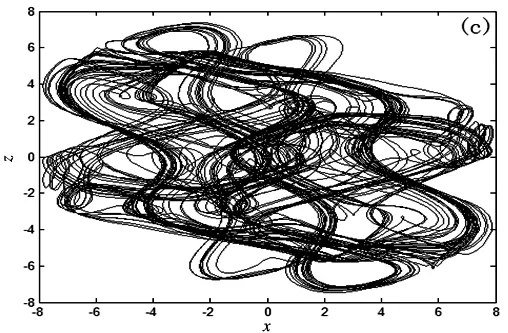

图1 当a=-2,b=6,c=3,d=-4,e=20,d1=40,b1=38时系统(3)的相图
2 新系统的混沌验证
2.1耗散性与吸引子的存在性
根据系统(3)的向量场散度
(4)
我们可以得到系统(3)是耗散的,也就是体积元v0在t时刻收缩到体积元V0e(2a+d)(t-t0),并且当t→∞时,系统(4)轨线的每个小体积元都以指数率2a+d收缩到0.系统(4)的轨线最终将被限制到体积为0的极限子集上,且被固定到1个吸引子上.
2.2对称性和不变性
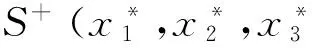
2.3有界性
若一个系统是有界的,并且它有一个正的Lyapunov指数,则我们称这个系统是混沌的.
定理1当a<0,c<0,d<0时,系统(3)有界.
证明把系统(3)写成下面的形式
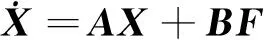
其中
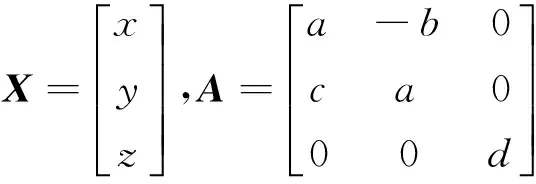
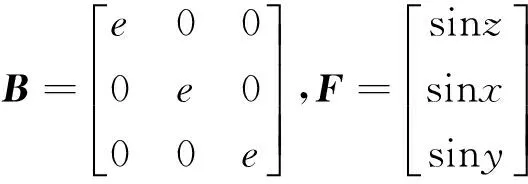
我们定义
V=XTX,
那么有

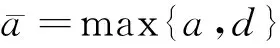

则


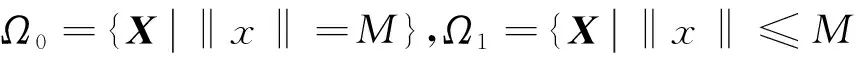
当‖x‖≥M时,我们得到
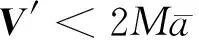
这说明系统(3)是有界的.
2.4平衡点的稳定性
平衡点是分析新系统的动力学特性的重要元素,首先我们要找到系统的平衡点. 因为系统(3)存在很多个平衡点,并且找到它的精确解非常困难.为便于研究,只考虑当平衡点为E0=(0,0,0)时的情况.
引理1多项式p(λ)=λ3+p1λ2+p2λ+p3的所有根都有负实部的充分且必要条件为p1,p2,p3都为正数,且满足不等式p1p2>p3.
定理2当满足条件
-(2a+d)>0,a2+2ad+bc+be>0,
a2d-bcd-bde-b1d1(c+e)>0,
-(2a+d)(a2+2ad+bc+be)
>a2d-bcd-bde-b1d1(c+e),
时,平衡点E0就是渐进稳定的.
证明因为系统 (3) 在E0=(0,0,0)处的Jacobian矩阵为
(5)
并且相应的特征多项式为
(6)
由引理1可以得到,平衡点E0是局部渐进稳定的充分必要条件是使公式(6)有负实部的特征根不等式,即a2+2ad+bc+be>0,2a+d>0,a2d-bcd-bde-b1d1(c+e)<0,且
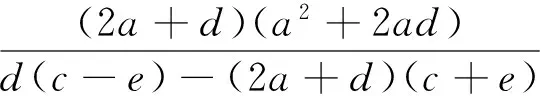
(7)
成立.因此当条件(7)满足时,我们可以得到E0=(0,0,0)是渐进稳定的.
3 系统(3)的Hopf分岔分析
系统(3)在平衡点E0处的Jacobian矩阵为

可以得到以下的线性函数:
B(x,y)=(0,0,0),C(x,y,z)=
(-d1x3y3z3,-ex1y1z1,-b1x2y2z2)
(8)
A0的特征值为
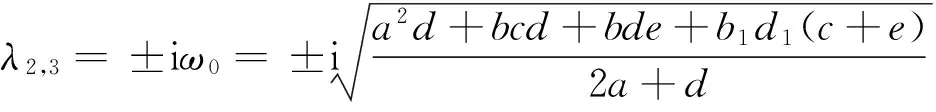
(9)
可得
(10)
P=(p1,p2,p3)T,
(11)
其中

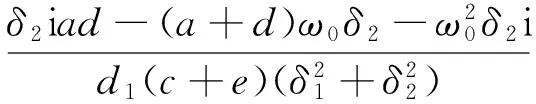

另外得
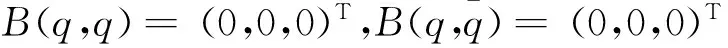
h11=(0,0,0)T,B(q,h11)=(0,0,0)T,
(12)
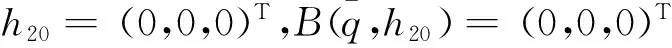

(13)
其中
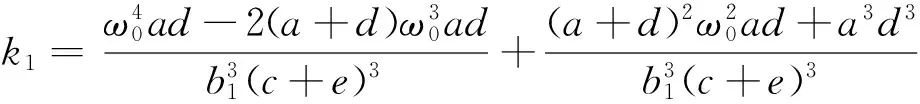
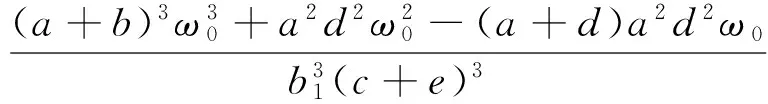


以及
=(-d1,-ek1-ek2i,-b1k3-b1k4i)
(14)

(15)
假设系统是随着参数b的变化而变化的,在临界值b=b0处我们有ξ′(b0)=Re
(16)
若ξ′(b0)≠0,那么Hopf分岔横截性条件成立.
定理3系统(3)在平衡点E0处的第一Lyapunov系数为
(17)
当l1≠0时,系统(3)在平衡点E0处发生Hopf分岔.特别地,若l1<0,系统发生超临界Hopf分岔;若l1>0,系统发生亚临界Hopf分岔.
4 数值仿真
为了更好地验证上面的分析结果,选a=-2,c=2,d=-2,e=1,b1=15,d1=-3,则Hopf分岔临界值b0=3.437 5. 当b=6.55>b0时,系统的平衡点是稳定的;当b=1.705>b0时,平衡点是不稳定的,分别如图2、4所示.通过计算得l1=128.311 62>0,ζ′(b0)=-0.224 6,也就是说横截条件成立.所以,系统(3)此时在平衡点E0处发生亚临界Hopf分岔,且产生一个不稳定的极限环,如图3所示.

图2 当a=-2,c=2,d=-2,e=1,b1=15,

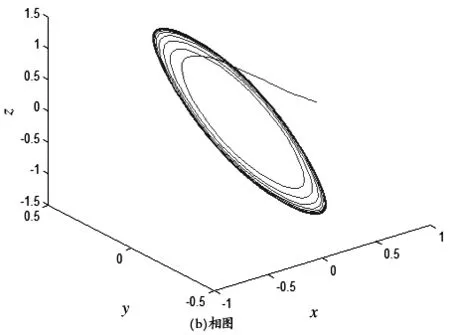
图3 当a=-2,c=2,d=-2,e=1,b1=15,
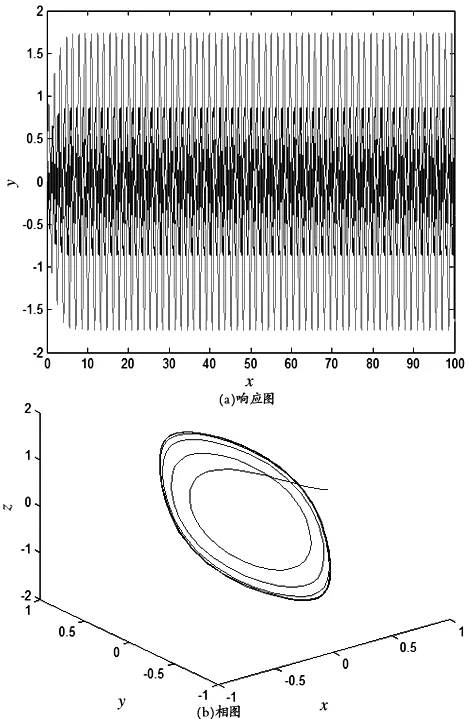
图4 当a=-2,c=2,d=-2,e=1,b1=15,
5 结语
本文通过混沌纠缠的方法人为构建了一个新的混沌系统,通过详细的理论推导和数值分析得出该系统存在混沌吸引子.此外,利用非线性动力学理论知识讨论了该系统平衡点的稳定性.通过Hopf分岔理论,对系统的Hopf分岔行为进行了详细分析,并且推导出系统产生Hopf分岔的参数条件.通过计算系统在平衡点的第一Lyapunov系数,判断了Hopf分岔的方向及其稳定性.
[1]LORENZEN.Deterministicnonperiodicflow[J].JournaloftheAtmosphericSciences, 1963(20):130-141.
[2]WATTSR.Globalwarmingandthefutureoftheearth[M].Morgan&Claypool, 2007.
[3]唐良瑞,李静,樊冰,等.新三维混沌系统及其电路仿真[J].物理学报, 2009, 58(2):785-793.
[4]李险峰,张建刚,褚衍东.一个新自治系统的动力学分析[J].复杂系统与复杂性科学, 2008,5(1):1672-3813.
[5]杜文举.VanderPol-Duffing系统的Hopf分岔分析及岔控制研究[D].兰州:兰州交通大学,2014.
[6]HUDP,CAOHJ.Bifurcationandchaosinadiscrete-timepredator-preysystemofhollingandleslietype[J].CommunNonlinearSciNumerSimulat, 2015,22:702-715.
[7]ZALMANB,HUQW.WieslawK.Globalhopfbifurcationofdifferentialequationswiththresholdtypestate-dependentdelay[J].JournalofDifferentialEquations, 2014,257:2622-2670.
[8]ZHANGHT,LIUXZ,SHENX,etal.Chaosentanglement:anewapproachtogeneratechaos[J].InternationalJournalofBifurcationandChaos, 2013, 23(5):1330014.
[9]HUZY,TENGZD,ZHANGL.StabilityandbifurcationanalysisinadiscreteSIRepidemicmodel[J].MathematicsandComputersinSimulation, 2014,97:80-93.
[10]WANGFX.Bifurcationsofnonlinearnormalmodesviatheconfigurationdomainandthetimedomainshootingmethods[J].CommunNonlinearSciNumerSimulat, 2015,20:614-628.
(责任编辑穆刚)
Hopf bifurcation investigation for a new chaos entanglement system
Kutorzi Edwin Yao, ZHANG Jiangang, QIN Shuang
(School of Mathematics and Physics, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China)
In this paper a new chaos entanglement system was proposed, and the theoretical analysis and numerical results show that chaos attractor exists in the system. In addition, the stability of equilibria and the existence and stability of the Hopf bifurcation were studied by using the theory of nonlinear dynamics. The direction and stability of the Hopf bifurcation were given by computing the first Lyapunov coefficient. Then, the numerical simulation is given to illustrate the theoretical analysis.
chaos entanglement; stability; Lyapunov coefficients; Hopf bifurcation
2016-04-12
国家自然科学基金项目(61364001).
Kutorzi Edwin Yao(1984—),男, 硕士研究生,主要从事非线性动力学方面的研究.
O415.5
A
1673-8004(2016)05-0024-05
[通讯简介]秦爽(1992—),黑龙江大庆人,硕士研究生,主要从事非线性动力学及其控制方面的研究.
