软硬岩互层边坡的破坏模式及稳定性研究

郑志勇，余海兵，徐海清,3

(1.中国地质大学(武汉) 工程学院，武汉　430074；2.中交第二公路勘察设计研究院有限公司 二分院　430050；3.武汉地铁集团有限公司 总工办，武汉　430030)



软硬岩互层边坡的破坏模式及稳定性研究

郑志勇1,2，余海兵1，徐海清1,3

(1.中国地质大学(武汉) 工程学院，武汉430074；2.中交第二公路勘察设计研究院有限公司 二分院430050；3.武汉地铁集团有限公司 总工办，武汉430030)

采用FLAC3D强度折减法研究软硬岩互层边坡在不同岩层厚度组合h、不同岩层倾角下边坡的破坏模式和稳定性系数k。结果表明h对边坡的破坏模式影响较小，θ对边坡的破坏模式影响明显:①水平层状边坡破坏模式为滑移—压致拉裂；随着θ的增大，顺倾向边坡破坏模式为滑移—拉裂、顺层滑移、滑移—溃曲、弯折—溃曲；直立边坡为弯折—崩塌破坏模式；反倾向边坡为滑移—溃曲和弯折—倾倒破坏模式。②缓倾向顺层边坡中，h的变化对边坡k影响很小，k由靠近坡脚处的软岩决定;其余层状边坡中，当软岩厚度不变时，k随着硬岩厚度的增大而增大，当硬岩厚度不变时，k随着软岩厚度的增大而减小。③随着θ的增大，顺倾向边坡中，k曲线呈现出先减后增的形状；反倾向边坡中，k曲线呈现出先增大后减小再增大的形状；软硬岩互层边坡总体稳定性趋势为，近直立层状边坡>陡倾向顺层边坡>反倾层状边坡>近水平层状边坡>缓倾向顺层边坡。

层状边坡；软硬岩互层边坡；破坏模式；稳定性；强度折减法

1　研究背景

在自然界中，层状沉积岩非常普遍，约占大陆陆地面积的70%，并且自然界中大多数层状边坡由软弱互层地层组成，其稳定性是制约工程建设的重要问题。如：三峡库区岸坡大量的顺层高边坡、锦屏一级水电站右岸肩槽的反倾层状高边坡、杭千高速公路建德段项目，在30km有余范围内共有39个顺层岩质滑坡；沪蓉高速公路存在着许多软硬岩互层路堑边坡。因此，研究软硬岩互层边坡的破坏模式和稳定性情况，对于边坡的稳定性评价和支护设计具有重要的现实意义。张倬元等[1]提出了6种斜坡变形破坏模式。程谦恭等[2]应用塑性极限分析方法，建立滑坡稳定性的判据。一些学者从模型试验的角度，根据相似理论建立出力学模式，对层状岩体的破坏特征进行了研究[3-5]。林杭等[6]基于FLAC3D数值模拟软件运用强度折减法研究层状边坡在不同岩层倾角对应下边坡的破坏模式和稳定性情况；蔡跃等[7]基于UDEC数值模拟软件，对反倾层状岩质边坡在各种因素的影响下的稳定性进行了分析。

本文尝试用FLAC3D强度折减法模拟分析软硬岩互层边坡(不同的岩层倾角、不同的软硬岩厚度组合)的破坏模式和稳定性情况。

2　强度折减法介绍

相比于极限平衡法，强度折减法具有不需事先假定滑动面，也能进行边坡应力—应变的分析等优点。该法始于20世纪70年代末，由英国科学家Zienkiewicz首先提出，国内学者中郑颖人等[8-10]、赵尚毅等[11-12]在强度折减法的判据和计算精度方面进行了大量研究，提高了该法的计算精度，并推广了该法的应用范围。其计算原理是将折减前的岩土体抗剪强度参数同时除以折减系数K，通过逐渐增大K，反复计算，直至边坡临界破坏，此时的折减系数即为稳定性系数。

强度折减法稳定性系数可表示为

式中：黏聚力c和内摩擦角φ为折减前的岩土体抗剪强度参数；c′，φ′为折减后的抗剪强度参数；k为折减后边坡处于临界状态的稳定性系数。

强度折减法的失稳判别标准目前主要有：数值计算的不收敛、塑性区的贯通、某特征部位位移的突变。裴利剑等[13]认为这3种判据具有内在统一性和一致性，其中以数值计算不收敛作为判别条件最为方便，也最为可靠；边坡的破坏模式通过临界状态下边坡的水平位移云图和速度矢量图2个指标进行综合判断。

3　FlAC3D数值模拟分析

3.1计算模型与参数

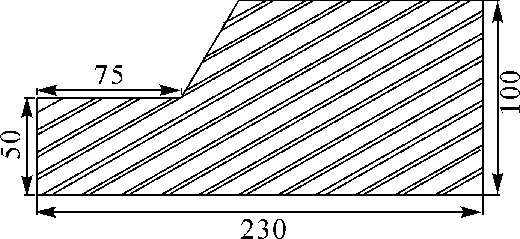
单位：m图1　计算模型Fig.1　Calculation model

数值模型中，硬岩和软岩均采用实体单元模拟，均按连续介质考虑，边坡角度为α=60°，岩层倾角θ为0°～90°，硬岩厚度h1范围为2～8m，软岩厚度h2为1～4m，计算模型的左边界到坡脚的距离为坡高的1.5倍，右边界至坡顶的距离为坡高的2.5倍，网格的尺寸满足计算精度要求；选用Mohr-Coulomb屈服准则；研究硬岩和软岩不同厚度组合、不同岩层倾角下边坡的破坏模式和稳定性情况。计算模型见图1，岩体力学参数见表1。

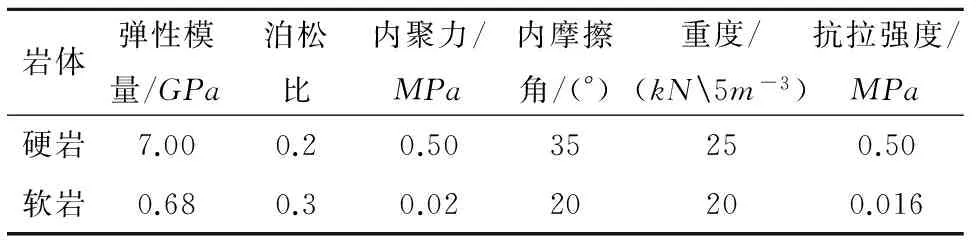
表1　物理力学参数Table 1　Physico-mechanical parameters of rock mass

3.2计算结果分析

3.2.1水平层状软硬岩互层边坡分析

3.2.1.1破坏模式分析

如图2所示(黑色箭头为速度矢量图)，上部岩体在重力作用下向下产生滑移。靠近坡脚部位岩体在重力分力的作用下沿坡脚剪出破坏，硬岩和软岩的厚度变化对边坡的破坏模式没有影响(本文以h=8∶2为例进行说明)，均属于滑移—压致拉裂破坏模式。

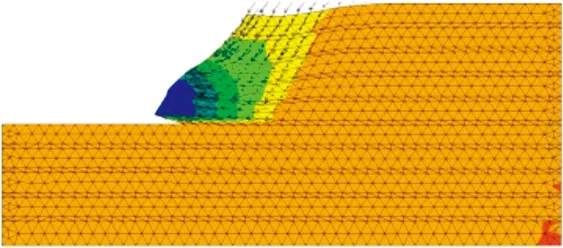
图2　水平层状软硬岩互层边坡破坏模式Fig.2　Failure mode of horizontally interbedded soft andhard rock slope

3.2.1.2稳定性分析

由表2可知，①由硬岩和软岩的组合：2∶2，4∶2，8∶2对应的稳定性系数可得，当软岩厚度h2=2m不变时，稳定性系数随着硬岩厚度h1的增大而增大；②由硬岩和软岩组合的厚度比：4∶1，4∶2，4∶4对应的稳定性系数可得，当硬岩厚度h1=4m不变时，稳定性系数随着软岩厚度h2的增大而减小；③由硬岩和软岩组合的厚度比：2∶2，4∶4，4∶1，8∶2对应的稳定性系数可知，当硬岩和软岩的比例相等时，稳定性系数的变化很小，因此对于硬岩和软岩互层的边坡可以在坡面附近按实际比例建模，其它部位可以通过适当的比例概化计算。

表2　水平层状不同岩层厚度边坡的稳定性系数Table 2　Relationship between thickness of rock layers andstability coefficient of horizontally interbedded slope

3.2.2顺倾向软硬岩互层边坡分析

3.2.2.1破坏模式分析

顺倾向软硬岩互层边坡破坏模式见图3。

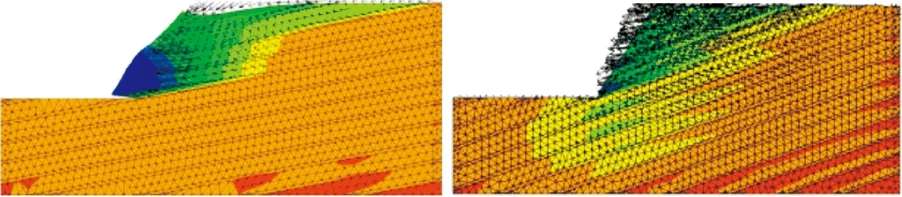
(a)θ=10°　　　　　　　　(b)θ=20°

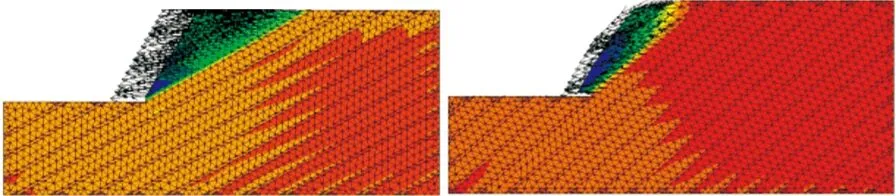
(c)θ=30°　　　　　　　　(d)θ=40°

(e)θ=50°　　　　　　　　(f)θ=60°

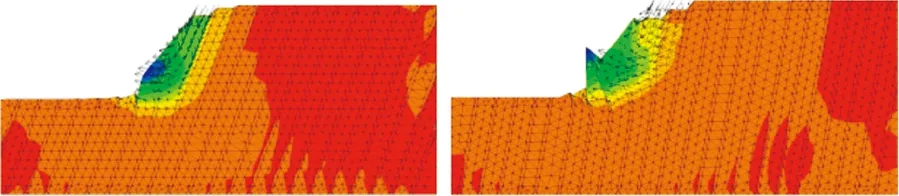
(g)θ=70°　　　　　　　　(h)θ=80°图3　顺倾向软硬岩互层边坡破坏模式Fig.3　Failure modes of consequent soft and hard rockslope of different dip angles

由图3可知，岩层倾角对边坡的破坏模式有很大影响：①当岩层倾角很小时，θ=10°(θ<φ<α)，由于边界条件的限制，边坡沿软岩层面向临空面方向蠕滑，并使滑移体拉裂解体，破坏模式为滑移—拉裂。②当岩层倾角缓倾时，θ∈[20°，50°](φ<θ<α)，靠近坡脚的软岩及上覆岩体发生整体滑移破坏，破坏模式为顺层滑移。③当岩层倾角等于或稍大于边坡角时，θ∈[60°，70°]，由于层面不具备临空条件，在重力作用下，岩层发生蠕变，上部岩体沿软岩向下滑移，下部岩体因此而产生向坡外的弯曲隆起变形，边坡的破坏从溃曲部位由外向内逐层推进，直至上部滑移岩体失去下部岩体的支撑而整体下滑，破坏模式为滑移—溃曲。④当岩层陡倾时，θ=80°(θ>α)，岩体和软弱层将会发生弯折变形，属于滑移—弯曲破坏模式。

3.2.2.2稳定性分析

(1)岩层倾角影响分析：硬岩和软岩不同组合下边坡的稳定性系数形状类似(见图4)，稳定性系数随着岩层倾角的增大，曲线呈现出先减后增的形状，即当坡角一定时，边坡存在一个最不利岩层倾角，θ=40°对应的稳定性系数最小。

(2)硬岩和软岩不同厚度组合影响分析：①当θ=10°时，硬岩和软岩的组合对边坡稳定性的影响规律和水平层状边坡相同；②当θ∈[20°，50°]时，硬岩和软岩的不同组合对边坡稳定性系数几乎无影响，稳定性系数曲线基本重合，其稳定性系数由靠近坡脚处的软弱结构面决定，因此对于此类边坡可以用概化模型计算；③当θ∈ [60°，80°]时，岩层厚度的变化对边坡的稳定性系数的影响比较敏感，对于这种软硬互层类型的边坡，可以在靠近边坡坡面附近的部位按实际比例进行建模计算。

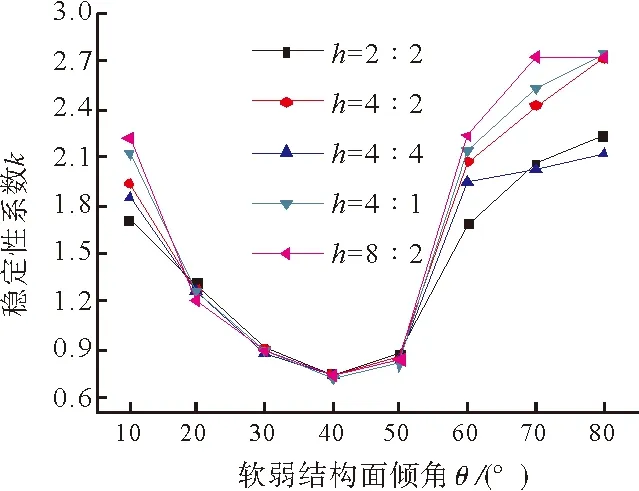
图4　顺倾向岩层倾角与边坡稳定性系数关系Fig.4　Relationship between dip angle and stabilitycoefficient of consequent slope

3.2.3直立层状软硬岩互层边坡分析

3.2.3.1破坏模式分析

见图5，上部岩层在重力分力作用下软岩向坡外弯曲变形，岩体在裂隙面上的剪应变累积起来从而导致板间拉裂，层间将有局部的陷落带出现，愈靠近坡顶位置，这种现象愈加明显，并逐渐塌落。硬岩和软硬的不同厚度组合对边坡的破坏模式影响较小，破坏模式为弯折—崩塌。

3.2.3.2稳定性分析

直立层状软硬岩互层边坡中硬岩和软岩不同组合对边坡稳定性系数的影响规律与水平层状软硬岩互层边坡大致相同。稳定性系数见表3。

图5　直立边坡软硬岩互层破坏模式Fig.5　Failure mode of vertically interbedded soft andhard rock slope表3　直立层状不同岩层厚度边坡的稳定性系数Table 3　Relationship between thickness of rock layers andstability coefficient of vertically interbedded slope

硬岩和软岩厚度比h1∶h2稳定性系数k2∶22.024∶22.384∶41.91硬岩和软岩厚度比h1∶h2稳定性系数k4∶12.838∶22.83

3.2.4反倾向软硬岩互层边坡分析

3.2.4.1破坏模式分析

反倾向软硬岩互层边坡破坏模式见图6。

(a)θ=10°　　　　　　　　　　(b)θ=20°

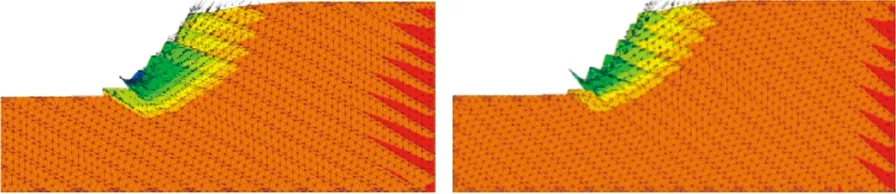
(c)θ=30°　　　　　　　　　　(d)θ=40°

(e)θ=50°　　　　　　　　　　　(f)θ=60°

(g)θ=70°　　　　　　　　　　　(h)θ=80°图6　反倾向软硬岩互层边坡破坏模式Fig.6　Failure modes of anti-dip rock slope of differentdip angles

由图6可知：当软岩倾角较小时，即θ∈[10°，30°]，岩体的弯折与溃曲变形程度均较弱，边坡沿坡脚底层台阶面滑出，θ越缓，位于坡脚地层坡面的剪出口位置相对越远。剪出口位置由靠近坡脚处的结构面所控制，并在该部位产生隆起，其破坏模式为滑移—溃曲。随着岩层倾角的增大，即θ∈[40°，80°]时，坡前缘沿软岩的剪切破坏趋势增强，板状岩体弯折变形程度逐渐增大，层状岩体产生向坡外的弯折变形，当剪应力大于岩体的抗拉和抗折强度时将发生折断，此类边坡属于弯折—溃曲破坏模式。

3.2.4.2稳定性分析

由图7可知:①对于反倾向层状边坡，硬岩和软岩不同组合下稳定性系数的形状类似，随着岩层倾角的增大，边坡的稳定性系数曲线呈现出先增后减再增的形状，即边坡存在一个最不利岩层倾角，根据软硬岩不同h对应下的稳定性系数，这个最不利θ∈[60°，70°]，对应的对边稳定性最差。②当硬岩和软岩比例为2∶2和4∶4时，对应的边坡的稳定性系数变化很小；当硬岩和软岩比例为4∶1和8∶2时，θ∈[10°，30°]时稳定性系数变化很小;θ∈[40°，80°]时稳定性系数变化较大，因此对于反倾边坡，坡面附近的软硬岩(特别是层面倾角较陡的)应按实际比例建模计算。

图7　反倾角岩层倾角与边坡稳定性系数关系Fig.7　Relationship between dip angle and stabilitycoefficient of anti-dip slope

综合图4和图7可得边坡稳定性总体趋势表现为：近直立层状边坡>陡倾向顺层边坡(θ>α)>反倾层状边坡>近水平层状边坡>缓倾向顺层边坡(φ<θ<α)。

4　结　论

(1)岩层倾角对软硬岩互层边坡的破坏模式影响较大，近水平层状边坡，其破坏模式为滑移—压致拉裂；顺倾向边坡，即θ∈[10°，80°]，随着θ的增大，破坏模式为：滑移—拉裂、顺层滑移、滑移—溃曲、弯折—溃曲；直立软硬岩互层边坡破坏模式为“弯折—崩塌”；反倾向边坡，当θ∈[10°，80°]时，其破坏模式为：滑移—溃曲和弯曲—倾倒。

(2)硬岩和软岩不同组合对边坡稳定性系数影响表现为：缓倾顺层坡，即θ∈[20°，50°]时，软岩或硬岩不同比例组合对边坡的稳定性影响很小，其稳定性系数由靠近坡脚处的软岩决定，对于此类边坡最危险滑面之上的坡体可以概化为一个整体计算。其余层状边坡，当软岩厚度不变时，边坡的稳定性系数随着硬岩厚度的增大而增大，当硬岩厚度不变时，边坡的稳定性系数随着软岩厚度的增大而减小；对于层状边坡为了得到相对准确的稳定性系数靠近边坡面附近的岩层厚度应按实际比例建模，其它部位可以根据合适的比例概化进行计算。

(3)岩层倾角对边坡的稳定性影响表现为：①顺层边坡，稳定性系数曲线呈现出先减后增的形状，即存在一个最不利岩层倾角，θ=40°时边坡安全系数最小；②对于反倾边坡，稳定性系数曲线呈现出先增大后减小再增大的形状，即存在一个最危险岩层倾角，根据软硬岩不同h对应下的稳定性系数，这个最不利θ∈[60°，70°]；③对于软硬岩互层边坡，其稳定性总体趋势表现为：近直立层状边坡>陡倾顺层边坡(θ>α)>反倾层状边坡>近水平层状边坡>缓倾顺层边坡(φ<θ<α)。

[1]张倬元,王士天,王兰生.工程地质分析原理[M].北京:地质出版社,1994.

[2]程谦恭,张倬元,黄润秋.侧翼与滑床复合锁固切向层状岩质滑坡动力学机理与稳定性判据[J]. 岩石力学与工程学报,2004,23(1):1874-1882.

[3]陈从新,黄平路,卢增木.岩层倾角影响顺层岩石边坡稳定性的模型试验研究[J].岩土力学，2007，28(3)：476-482.

[4]唐红梅,陈洪凯,曹卫文.顺层岩体边坡开挖过程模式实验[J].岩土力学,2011,32(2):435-440.

[5]卢增木,陈从新,左保成,等.对影响逆倾层状边坡稳定性因素的模式实验研究[J].岩土力学,2006，27(4)：629-632.

[6]林杭,曹平,李江腾,等.层状岩质边坡破坏模式及稳定性的数值分析[J].岩土力学,2010,31(10):3300-3304.

[7]蔡跃,三谷泰浩,江琦哲郎.反倾层状岩体边坡稳定性的数值分析[J].岩石力学与工程学报,2008,27(12):2517-2522.

[8]郑颖人,赵尚毅,宋雅坤.有限元强度折减法研究进展[J].后勤工程学院学报,2005,21(3):1-6.

[9]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用明[J].岩石力学与工程学报,2004,23(19):3351-3388.

[10]郑颖人,赵尚毅,邓卫东.岩质边坡破坏机制有限元数值模拟分析[J].岩石力学与工程学报,2003,22(12):1943-1952.

[11]赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

[12]赵尚毅,郑颖人,张玉芳.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.

[13]裴利剑,屈本宁,钱闪光.有限元强度折减法边坡失稳判据的统一性[J].岩土力学,2010,31(10):3337-3341.

(编辑：刘运飞)

Numerical Analysis of Failure Modes and Stability of Soft and Hard RockInterbedded Slope

ZHENG Zhi-yong1,2, YU Hai-bing1, XU Hai-qing1,3

(1.FacultyofEngineering，ChinaUniversityofGeosciences，Wuhan430074，China;2.TheSecondBranch,CCCCSecondHighwayConsultantCo.Ltd.,Wuhan430050，China;3.ChiefEngineerOffice,WuhanMetroGroupCo.Ltd.,Wuhan430030，China)

Thefailuremodesofsoftandhardrockinter-beddedslopeweresimulatedbyFLAC3D,andthestabilitycoefficientkinthepresenceofdifferentdipanglesθandrockthicknesseshwasanalyzedbyusingstrengthreductionmethod.Resultsshowthathhassmallinfluenceonslopefailuremode,whileθhasobviouseffectonthefailuremode.Forhorizontallylayeredslope,thefailuremodeisslipping-ripping;whereasforconsequentslope,withtheincreaseofθ,thefailuremodeexperiencesaprogressofsliding-ripping,sliding,sliding-buckling,andbending-buckling;whileforverticallylayeredslope,thefailuremodeisbending-slump;andforanti-diprockslope,thefailuremodesaresliding-bucklingandbending-toppling.Moreover,forgentlebeddingrockslope,thethicknessoftherockhaslittleimpactonthestabilitycoefficientk,whichisdeterminedbythesoftrockneartheslopetoe.Asfortheothertypesoflayeredslope,whenthethicknessofsoftrockisconstant,thestabilitycoefficientincreaseswiththeincreaseofhardrockthickness,whilewhenhardrockthicknessisconstant,thestabilitycoefficientdecreaseswiththeincreaseofsoftrockthickness.Withtheincreaseofθ,thekvalueofconsequentslopefirstdecreasesandthenincreases,whilethekvalueofanti-diprockslopeincreasesandthendecreasesandfinallyincreases.Theoverallstabilityofsoftandhardrockslopefollowstheorderofverticallayeredslope>steepbeddingrockslope>anti-dipslope>horizontallayeredslope>gentlebeddingrockslope.

layeredslope；inter-beddingsofsoftandhardrock；failuremode；stability；strengthreductionmethod

2015-08-10;

2015-09-03

郑志勇(1977-)，男，江西会昌人，高级工程师，硕士，主要从事公路边坡稳定性分析及岩土工程数值模拟等方面的研究工作，(电话)13971503087(电子信箱)624482980@qq.com。

余海兵(1987-)，男，湖北咸宁人，助理工程师，硕士，主要从事边坡稳定性分析及岩土工程数值模拟等方面的研究，(电话)18071715799(电子信箱)haibyu@163.com。

10.11988/ckyyb.20150661

2016,33(09):102-106

P642

A

1001-5485(2016)09-0102-05