基于数值流形法的重力坝抗滑稳定性分析

陈远强，郑　宏，陈　涛

(1.三峡大学 土木与建筑学院，湖北 宜昌　443002；2.北京工业大学 建筑工程学院，北京　100124)



基于数值流形法的重力坝抗滑稳定性分析

陈远强1，郑宏2，陈涛1

(1.三峡大学 土木与建筑学院，湖北 宜昌443002；2.北京工业大学 建筑工程学院，北京100124)

作为一种新的数值方法，数值流形法在重力坝抗滑稳定性方面的研究较少。首先给出了水压及扬压力的荷载矩阵、安全系数的求解方法，然后采用数值流形法分析了重力坝沿建基面及深层双斜面的抗滑稳定性，得出了安全系数，并与有限元接触分析的结果进行了对比。分析结果表明：采用数值流形法和有限元接触分析法得到的安全系数基本一致，从而验证了数值流形法在重力坝抗滑稳定分析中的可行性。

数值流形法；重力坝；抗滑稳定分析；安全系数

1　研究背景

混凝土重力坝是我国水利水电工程建设中广泛采用的重要坝型之一，而抗滑稳定分析又是重力坝设计中的一项重要内容，因此采用合适的方法评价重力坝的稳定性具有十分重要的意义。

对于重力坝抗滑稳定的分析方法，我国现行重力坝设计规范规定：以刚体极限平衡法计算为主，必要时可辅以有限元法等其它方法[1]。刚体极限平衡法操作简单，具有长期实践经验，计算得出的整体抗滑稳定安全系数相对是可靠的，但不能模拟复杂地基对坝体稳定性的影响，且无法得到坝体及地基内应力和位移情况[2]；有限元方法能够求得坝体及坝基内的应力分布、软弱结构面受力,以及破坏情况，但存在计算量大和计算难以收敛的问题，且有限元构造的位移函数是协调的，无法很好地模拟不连续变形[3]。

数值流形法(NumericalManifoldMethod,NMM)是石根华博士在块体理论和非连续变形分析的基础上创立的，该方法以拓扑流形和微分流形为基础，采用数学覆盖和物理覆盖，能够统一解决工程中的连续与非连续变形问题[4]。该方法在处理各种复杂边界和不连续界面等方面具有巨大优势，因此，在岩土工程中得到广泛应用[5-7]。

本文推导了水压及扬压力的荷载矩阵，并基于数值流形法，对重力坝沿建基面及深层双斜面的抗滑稳定性进行了分析和评价。

2　数值流形法的基本原理

2.1有限覆盖及覆盖函数

数值流形法的物理覆盖系统由数学覆盖和物理网格两者组成，数学覆盖由用户选择，只定义近似解的精度；物理网格是由材料体的边界、裂缝、块体和不同材料区域的交接面所构成。物理覆盖重叠的公共部分形成流形单元[8]。

数值流形法在各个物理片上独立定义局部位移函数，即

Ui=[ui(x,y)vi(x,y)]T=PiDi。

(1)

式中：Pi为控制局部位移函数的基函数矩阵；Di为广义自由度。这些局部位移函数可以是常量、线性的、高阶多项式或级数的有限项。

局部位移函数通过权函数联结在一起，构成总体位移函数，即

(2)

式中：we(i)(x,y)为权函数；Ti为位移矩阵；q为物理片的个数。

2.2平衡方程

由给定的位移公式(2)，可以求出系统的总势能∏(包括应变势能、初应力势能、点荷载势能、线荷载势能、体荷载势能、惯性力势能、接触弹簧的应变势能和摩擦力势能)，再根据最小势能原理可建立平衡方程[9]，即

KD=F。

(3)

其中:

(4)

B=[LT1,LT2，…,LTq]。

(5)

式中：K为刚度矩阵；F为荷载矩阵，文献[8]给出了常见荷载类型的计算方法；Ω为求解区域；E为弹性矩阵；L为应变微分算子。

3　水压力及扬压力作用时的荷载矩阵

图1　作用有水压力的单元Fig.1　Element with water pressure

原有的数值流形法中并没有考虑水压及扬压力荷载的作用，对大坝进行抗滑稳定分析需要考虑这些荷载的作用。在此，利用能量原理进行推导。

设某流形单元的一条边上作用有分布荷载，如图1。

对于分布荷载段上某点s(x,y)，其参数方程可表示为

(6)

式中：(xk,yk)，(xk+1,yk+1)分别为k,k+1点的坐标。

点s处的水压力为

(7)

式中：qx，qy为对应点处水压力作用分量；ls，k为点s到点k的距离；lk,k+1为点k到点k+1的距离。

水压力产生的分布势能可表示为

(8)

(9)

当单元上作用有扬压力时，式(9)可同样求出由扬压力引起的单元节点荷载，扬压力的分布如图2所示。图中H1，H2分别为上、下游水深；γ为水的重度；α为折减系数。

(a)建基面扬压力分布

(b)深层双斜面扬压力分布图2　扬压力分布Fig.2　Distribution of uplift pressure

4　安全系数的求解

重力坝的整体安全状况可通过抗滑稳定整体安全系数来评价。计算安全系数时，参照传统有限元方法，先运用数值流形法对重力坝进行应力分析，根据得出的应力计算出可能滑动面上的正应力和剪应力，从而可得出滑动面上的抗滑力和滑动力，各自进行叠加，再仿照传统的刚体极限平衡法，可计算得到安全系数[10]，即

(10)

式中：σi，τi为滑动面上第i个单元的正应力和剪应力；fi，ci为滑动面上第i个单元的抗剪断摩擦系数和黏聚力；li为滑动面上第i个单元的长度；n为滑动面上单元的个数。

5　工程算例

5.1算例1：重力坝沿建基面的抗滑稳定分析

某混凝土重力坝坝高103m，坝顶宽14.8m，坝底宽度为70.24m，坝体断面具体尺寸如图3(a)所示。上游水位100m，下游无水。模型计算范围为：坝基自坝踵向上游取1.5倍坝高，自坝址向下游取1.5倍坝高，坝基深度取1倍坝高，具体计算模型及数学覆盖如图3(b)所示。约束条件为：上下游基岩施加法向约束，底部施加全约束。计算荷载考虑大坝及坝基自重、水压力以及扬压力。重力坝坝体弹性模量30.0GPa，泊松比0.20，密度2 630kg/m3；坝基岩体弹性模量19.5GPa，泊松比0.25，密度2 720kg/m3；坝体与坝基接触面的抗剪断摩擦系数与黏聚力分别为0.9和1MPa。

(a)坝体尺寸

(b)计算模型及数学覆盖图3　算例1坝体尺寸与数学模型覆盖Fig.3　Size of the dam and mathematical cover forexample 1

数值流形法中采用加减弹簧来模拟不连续界面的接触状态，故而本文用有限元接触分析来与之进行结果比对，水平向与竖直向位移对比见图4和图5，具体结果对比见表1。由结果分析可知：2种算法得到的位移大小基本一致，最大位移出现的位置相同：最大水平位移均出现在坝顶处，最大竖向位移均出现在下游面处。同时，二者计算得出的安全系数差别很小，说明对重力坝采用数值流形法进行分析是可行的。

(a)数值流形法

(b)有限元接触分析法图4　不同算法水平位移对比Fig.4　Comparison of calculated horizontal displacementbetween NMM and FEM contact analysis

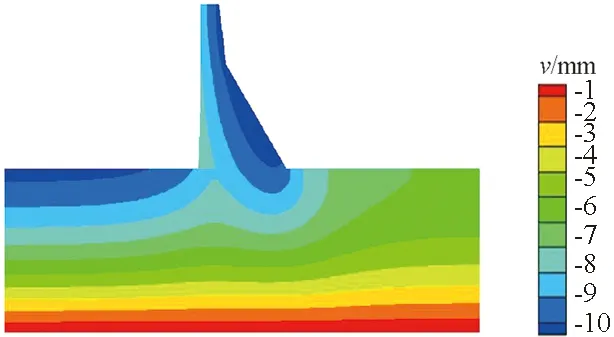
(a)数值流形法

(b)有限元接触分析法图5　不同算法竖直位移对比Fig.5　Comparison of calculated vertical displacementbetween NMM and FEM contact analysis表1　不同算法结果比较Table 1　Comparison of calculated results between NMMand FEM contact analysis

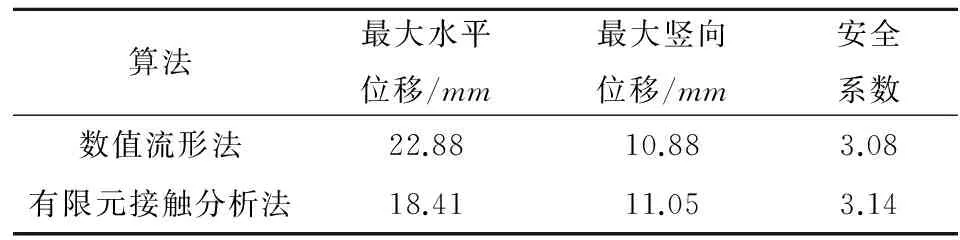
算法最大水平位移/mm最大竖向位移/mm安全系数数值流形法22.8810.883.08有限元接触分析法18.4111.053.14

5.2算例2：重力坝深层双斜面抗滑稳定分析

某重力坝非溢流坝段坝顶高程964.5m，坝高28m，坝顶宽8m，上游水位962.0m，下游水位941.0m。基岩内存在发育断层F5和小断层f3，形成坝基深层抗滑稳定的控制面，其中：断层F5与水平面夹角为22°，小断层f3与水平面夹角为28°，滑动示意图如图6(a)所示。

模型计算范围为：坝基长度自坝踵向上游取2倍坝底宽度，自坝址向下游取2倍坝底宽度，坝基深度取1倍坝高，具体计算模型及数学覆盖见图6(b)。约束条件为：上下游基岩施加法向约束，基岩底部施加全约束。计算荷载包括大坝及坝基自重、上下游水压力及扬压力，排水幕处的渗透压力折减系数为0.35。

坝体混凝土弹性模量为22GPa，泊松比为0.18，重度为24.0kN/m3；坝基岩体岩性单一，弹性模量为12.3GPa，泊松比为0.20，重度为25.4kN/m3；发育断层F5和小断层f3的抗剪断摩擦系数分别为0.25和0.70，黏聚力分别为0.05MPa和0.40MPa。

数值流形法得出的应力云图见图7，与有限元接触分析的具体结果对比见表2。经比较分析：两种算法的位移分布同样是一致的，最大水平位移出现在断层F5上部，最大竖向位移出现在坝顶处；安全系数相当接近，进一步验证了数值流形法对重力坝稳定分析的适用性。

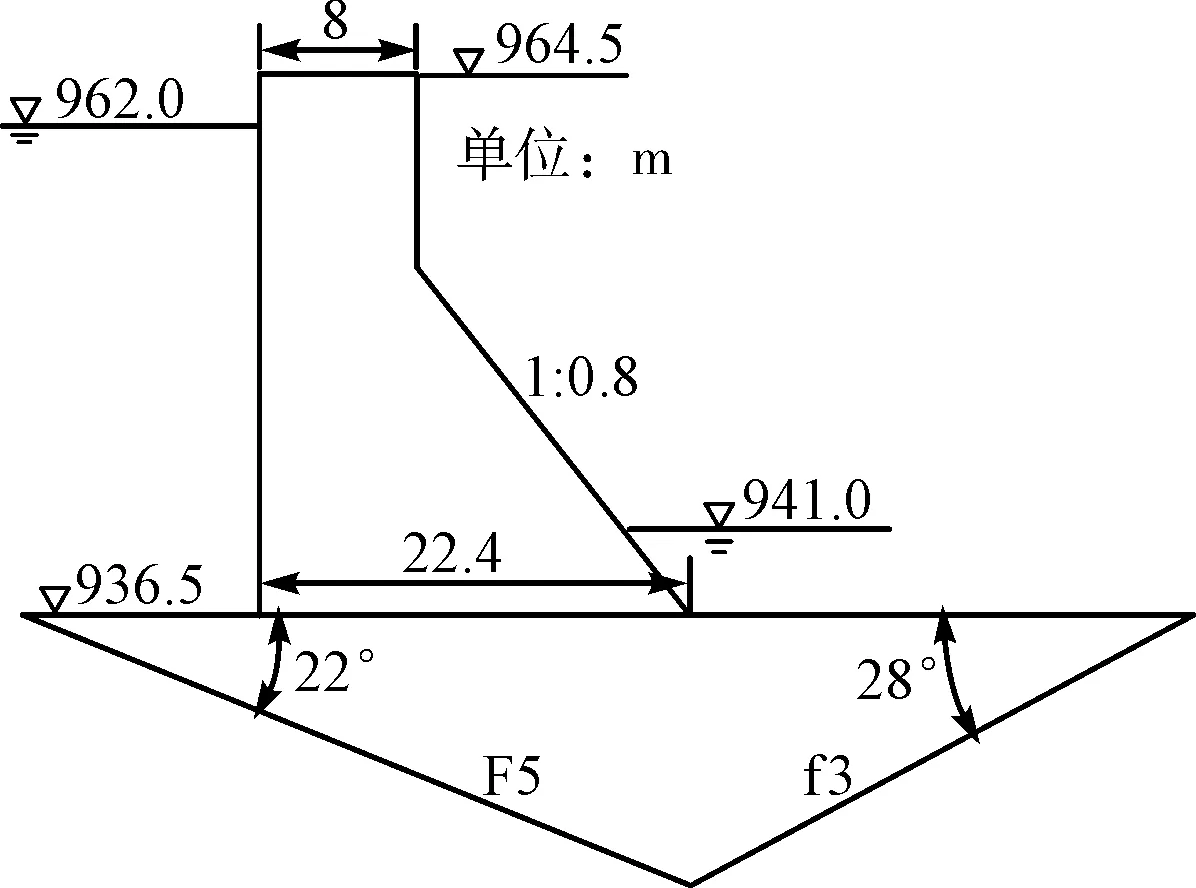
(a)双斜面滑动示意图

(b)计算模型及数学覆盖图6　算例2双斜面滑动与数学模型覆盖Fig.6　Sketch of double-inclined planes and mathematicalcover for example 2

(a)水平向应力

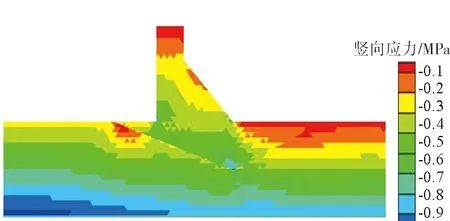
(b)竖向应力

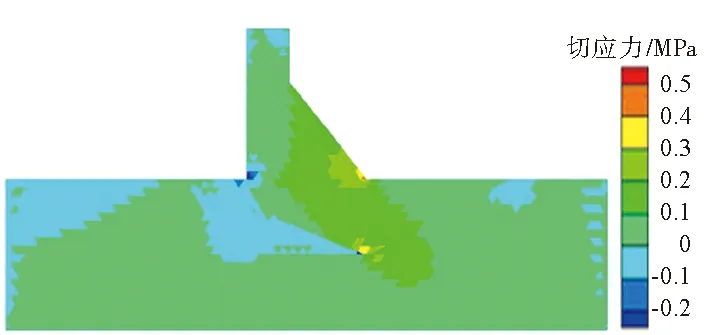
(c)切应力图7　数值流行法的应力云图Fig.7　Contours of stress calculated by NMM表2　不同算法结果比较Table 2　Comparison of calculated results between NMMand FEM contact analysis

算法最大水平位移数值/mm位置最大竖向位移数值/mm位置安全系数数值流形法0.94F5上端1.75坝顶5.73有限元接触分析法1.07F5上端1.84坝顶6.07

6　结　论

本文将数值流形法应用到重力坝沿建基面及深层双斜面抗滑稳定分析的工程算例中，通过与有限元接触分析的结果比较，得出以下结论：

(1)数值流形法计算得出的位移和应力分布与有限元接触分析结果基本一致，体现了数值流形法对工程中连续与非连续问题的可靠性。

(2)在数值流形法求解应力和引入刚体极限平衡法求安全系数的基础上，计算了重力坝的抗滑稳定安全系数，结果验证了数值流形法在重力坝抗滑稳定分析中的可行性。

[1]SL319—2005，混凝土重力坝设计规范[S].北京：中国水利水电出版社，2005.

[2]张国新,金峰.用DDA进行重力坝稳定安全分析[J].水力发电学报,2004，(1):10-14.

[3]王义锋，章青.基于界面元法的向家坝重力坝深层抗滑稳定分析[J].岩石力学，2009,30(9)：2691-2696.

[4]SHIGen-hua.ManifoldMethodofMaterialAnalysis[C]∥Transactionsofthe9thArmyConferenceonAppliedMathematicsandComputing.ArmyResearchOffice,Minnesota,June18-21,1991:57-76.

[5]王水林，葛修润.流形元方法在模拟裂纹扩展中的应用[J].岩石力学与工程学报，1997,16(5)：405-420.

[6]王书法，朱维申，李术才，等.加锚岩体变形分析的数值流形方法[J].岩石力学与工程学报，2002,21(8)：1120-1123.

[7]张国新，金峰，王光纶.用基于流形元的子域奇异边界元法模拟重力坝的地震破坏[J].工程力学，2001,18(4)：18-27.

[8]石根华.数值流形方法与非连续变形分析[M].裴觉民，译.北京：清华大学出版社，1997.

[9]王芝银，李云鹏.数值流形法中的几点改进[J].岩土工程学报，1998,20(6)：33-36.

[10]张国新，金峰.重力坝抗滑稳定分析中DDA与有限元方法的比较[J].水利发电学报，2004,23(1)：11-14.

(编辑：刘运飞)

Analysis of Anti-sliding Stability of Gravity Dam Using Numerical Manifold Method

CHEN Yuan-qiang1, ZHENG Hong2, CHEN Tao1

(1.CollegeofCivilEngineering&Architecture,ChinaThreeGorgesUniversity,Yichang443002,China;2.CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China)

TheNumericalManifoldMethod(NMM),asanewnumericalmethod,hasseldombeenutilizedintheanti-slidingstabilityanalysisofgravitydam.Inthisstudy,theloadmatrixofwaterpressureandupliftpressure,aswellasthesolutionofsafetyfactorweregiven.Furthermore,NMMwasadoptedtoanalyzetheanti-slidingstabilityofthefoundationplanesofgravitydamandthedeeply-laiddouble-inclinedplanes,thesafetyfactorwasthuscalculated,andwasfurthercomparedwiththecorrespondingresultsobtainedbythecontactanalysisinfiniteelementmethod(FEM).Theresultsdemonstratedthatthesafetyfactorscalculatedbytheabovetwomethods,namelytheNMMandFEM,werefundamentallyconsistent,whichverifiedthefeasibilityofapplyingNMMtotheanti-slidingstabilityanalysisofgravitydam.

numericalmanifoldmethod;gravitydam;stabilityanalysisagainstsliding;safetyfactor

2015-08-05;

2015-09-09

陈远强(1990-)，男，湖北随州人，硕士研究生，主要从事数值流行法方面的研究，(电话)18602707189(电子信箱)691205842@qq.com。

郑宏(1964-)，男，湖北南漳人，研究员，博士生导师，主要从事计算岩土力学研究，(电话)13986011345(电子信箱)hzheng@whrsm.ac.cn。

10.11988/ckyyb.20150655

2016,33(09):133-137

TV145

A

1001-5485(2016)09-0133-05