武汉地区厚互层土中基坑抗突涌破坏评价方法研究

熊宗海，冯晓腊，张红章，范卫琴，程华强

(1.武汉丰达地质工程有限公司，湖北 武汉 430074；2.中国地质大学(武汉)工程学院，湖北 武汉 430074；3.武汉市桥梁工程有限公司，湖北 武汉 430074)

基坑坑底以下有水头高于坑底的承压水含水层时，在承压水作用下坑底易发生突涌灾害或上浮失稳[1]，特别是在武汉、上海、杭州等城市[2]。由于存在相对隔水层，基坑坑底的突涌通常假定为整体顶升[3-6]，并且可用压力平衡法、均质连续梁板法和数值模拟[7]计算抗突涌安全系数；也有的试验认为是先出现裂隙，再产生渗透破坏[8]。在《建筑基坑支护技术规程》(JGJ120—2012)[9]中，规定突涌稳定性安全系数不应小于1.1。《岩土工程勘察规范》(GB 50021—2001)(2009年版)3.3.6条[10]规定，对同一土层中相间呈韵律沉积，当薄层与厚层的厚度比大于1/3时，宜定为“互层”。武汉的互层土由黏土、粉质黏土、粉土和粉细砂组成[11]，兼具隔水层与含水层的性质。出于工程安全考虑，在基坑抗突涌验算时常将互层土与下部砂土含水层看作整体的承压含水层。这种做法明显和实际不符，如武汉长江隧道江北明挖段在开挖基坑内厚互层土层时，突然停电，导致基坑内降水井的水位迅速攀升至坑底以上3 m位置，然而坑底厚互层土层并未出现开裂或涌水、涌砂现象。在恢复供电之前基坑一直处于稳定状态。由此可见，单纯将厚互层土作为承压含水层考虑十分保守，造成浪费。

丁春林等[12]分析了坑底弱透水层厚度、土黏聚力和内摩擦角等因素对基坑突涌塑性破坏的影响，得出坑底弱透水厚度和土黏聚力与坑底土突涌塑性破坏成非线性反比关系。李军等[13]通过简易的基坑突涌物理试验，张飞等[14]通过突涌离心模型试验，均验证了基坑基底中间部位最先发生破坏的现象。王军玺等[15]在Biot固结理论基础上，建立了基坑突涌分析水力劈裂耦合模型，得出突涌始于基底隔水层所发生的张拉破坏，初始张拉裂缝的水压楔劈效应所导致的水力劈裂为基坑突涌提供了通道。李瑛等[16]基于坑底土体沿铅垂面整体剪切破坏的假定，提出可考虑坑底土体抗剪强度、深坑几何尺寸和坑底加固的突涌稳定性计算公式，得出坑底隔水层的侧面积和顶面积的比值越大，突涌稳定性越好。

由此可见，将隔水层作为整体研究的较多，考虑厚互层土抗突涌的研究较少。本文从实际出发，考虑土体的重度、黏聚力、土体间的摩擦力并把厚互层土视为隔水层，建立了厚互层土基坑抗突涌稳定性分析模型，并提出相应的突涌稳定性安全系数计算公式，比目前规范规定的分析方法更接近实际，为重新定义互层土在基坑抗突涌稳定性中的作用进行了有益探索。

1 厚互层土突涌破坏判别方法

互层土主要由黏性土隔水层与砂性土含水层交互构成，可以视为多个薄层承压含水层组成的体系。因此抗突涌稳定性分析时，可以对厚互层土中每个薄层承压水含水层进行计算分析，根据突涌不稳定薄层承压含水层的受力情况，再进一步判断基坑是否存在整体突涌的风险，具体如下：

(1)当计算结果表明抗突涌不稳定仅局限于厚互层土小范围时，应当判定此时基坑不会发生突涌，即处于稳定状态。如果抗突涌不稳定区域只在厚互层土顶部，并未深入互层土含水层中，其少数几个薄层承压水含水层赋存水量十分有限，因此往表现为互层土顶部的少量释水而形成“流水”、“流砂”现象(图1)。此时突涌的水量会迅速衰减，由于无持续水源，表层突涌并不会影响工程的质量与安全。所以这种情况下，可以认定为基坑未发生坑底突涌灾害。

(2)当计算结果表明厚互层土含水层突涌不稳定区域贯通至下部砂层时，则应当判定为基坑发生突涌。此时发生突涌的范围将与下部高承压含水砂层贯通，基坑将出现持续不断的大量涌水涌砂，会严重影响工程的施工，甚至威胁基坑的安全，如武汉市江汉区常青路中石油大厦就是由于坑底长时间大量涌水冒砂导致基础难以施工。

2 关于将厚互层土层视为隔水层的证明

2.1 互层土基坑突涌发展模式

根据土层的沉积动力由强到弱，颗粒由粗到细，建立互层土层模型(图2)，底部为砂土层，属透水层；中间为砂土和黏土的厚互层土；上部为黏土层，属于隔水层。设厚互层土层上覆黏土厚度为b，互层土层中黏性土各层厚度由上至下的厚度依次为h1，h2，h3，…，hn-1，hn，互层土层中砂性土各层厚度依次为H1，H2，H3，…，Hn-1，Hn，且互层土中各砂层水头高度一致，高出互层土顶部的距离均为a。

对于互层土中第n-1层砂性土，其承压水对上部土层的水压力为：

(1)

式中：Pn-1——第n-1层砂性土对上部土层的水压力；

hi——第i层黏性土层厚；

Hi——第i层砂性土层厚；

γw——水的重度。

第n-1层砂性土上部土层因自重引起的抗力为：

(2)

式中：Rn-1——n-1层砂性土上部土层的自重应力；

γb——互层土上覆黏土重度；

γh——互层土中黏性土重度；

γH——互层土中砂性土重度。

根据压力平衡法[1]，第n-1层砂性土的抗突涌安全系数kn-1为：

(3)

若kn-1=1，即第n-1层砂性土上覆土层处于临界状态。那么对于第n层砂性土来说，其对上部土层的水压力：

Pn=Pn-1+(hn+Hn-1)·γw

(4)

第n层砂性土上部土层因自重引起的抗力为：

Rn=Rn-1+hn·γh+Hn-1·γH

(5)

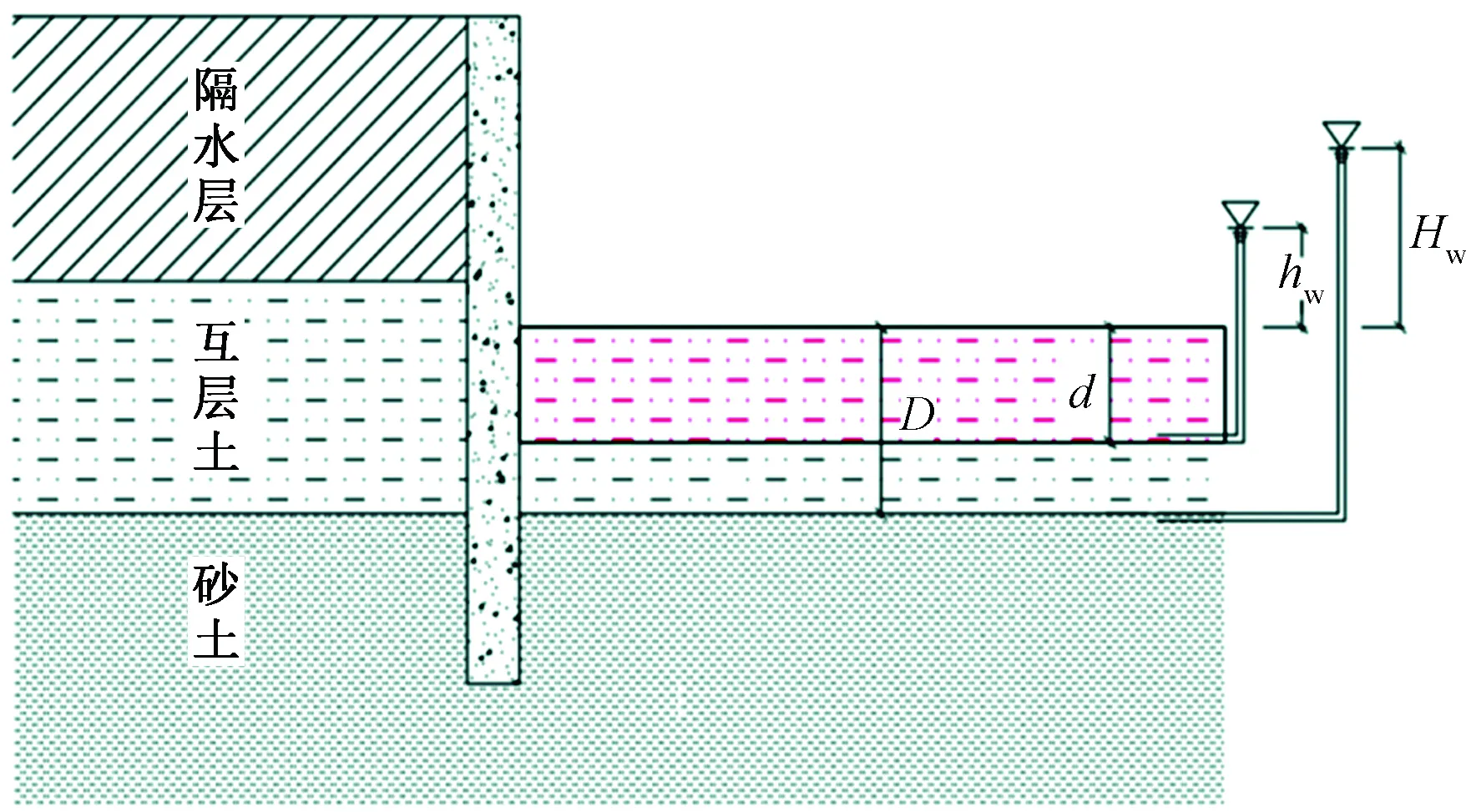
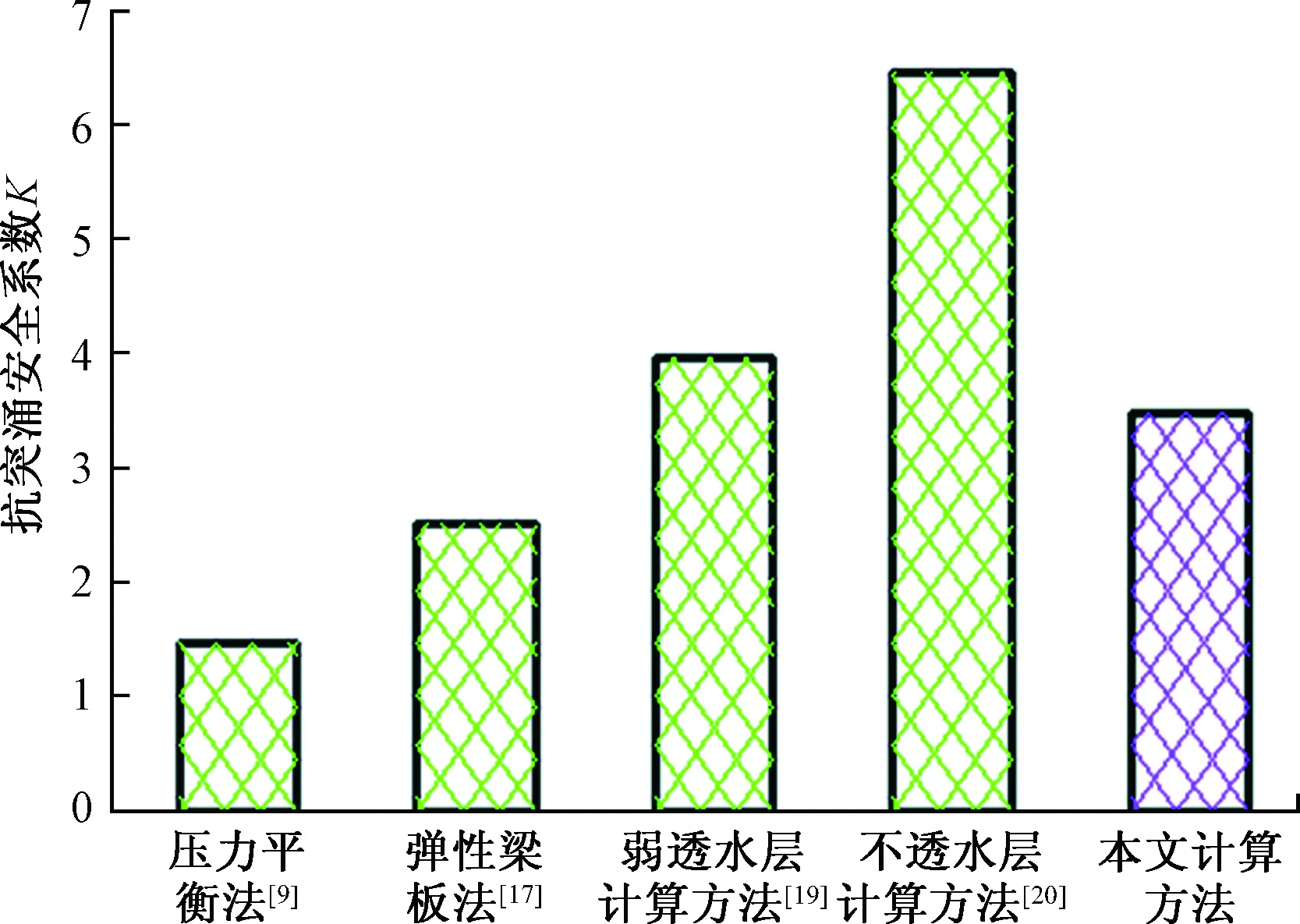
由于互层土中黏性土与砂性土的重度要大于水的重度，即γh>γw，γH>γw，显然有Pn

(6)

因此当第n-1层砂性土上覆土层处于抗突涌稳定的临界状态时，以第n层砂性土计算，土层应处于稳定状态，不会发生基坑突涌。同理可证明，互层土中第n层砂性土下方土层均为抗突涌稳定。抗突涌不稳定区域仅在第n-1层砂性土层及上覆土层，而其下方的互层土层处于稳定状态。

由此可见，互层土并非整体达到抗突涌不稳定，而是逐层发展。如果其抗突涌不稳定区域仅局限在互层土上层部分薄层中时，应当判定为基坑整体处于稳定状态。

2.2 武汉地区互层土基坑突涌不稳定范围

武汉地区互层土的平均天然重度为17～19 kN/m3，互层土中砂性土的承压水头高出互层土顶部1～2 m。水的重度取10 kN/m3，其典型断面土体参数如表1所示。

随着土体不断的开挖，互层土中抗突涌不稳定的区域逐渐向下部拓展，因此当上覆不透水黏土层被完全挖除后，其抗突涌临界状态范围达到最大，此时：

Rn=H·γH

(7)

Pn=(a+H)·γw

(8)

式中：H——第n层砂性土上部互层土的厚度；

γH——互层土的天然重度。

表1 武汉地区典型互层土分布情况Table 1 Typical Distribution of inter bedded soil engineering in Wuhan

当Rn=Pn时，求得极限厚度Hmax为2.0～3.0 m。即在开挖互层土上覆不透水黏土层整个过程中，互层土出现突涌不稳定的范围集中于顶部2.0 m厚度范围内，而武汉地区大部分深厚互层土的厚度在7～12 m间，局部甚至可达20 m。因此对于发育有深厚互层土的基坑，在开挖互层土上覆土层过程中，互层土突涌不稳定区域只在其顶部小部分范围内，而其下部大部分仍然处于稳定状态，表现出隔水层的性质。在此种情况下，如将互层土作为承压含水层进行抗突涌验算显然是不合理的，应当将其作为隔水层处理。

3 互层土基坑突涌计算模型及公式

根据土体渗透破坏类型，坑底突涌可分为面积力失稳破坏和体积力失稳破坏，如图3所示，图中F为承压含水层水压力，J为渗透力。

图3 基坑渗透破坏受力验算示意图Fig.3 Schematic diagram of foundation pit seepage failure calculation

针对某一种上覆土层只能采用其中一种计算分析方法，这是由于渗透体积力是孔隙水压力梯度的体现，反映了孔隙水压力的变化规律。而此时，上覆土底部水压力与土体内部孔隙水压力自平衡，因此不能再计入接触面的面积力[4]。实际工程中，面积力失稳表现为坑底土表面出现网状裂缝；体积力失稳则表现为坑底涌水、涌砂。对于坑底为弱透水互层土的基坑，基坑突涌形式常常为后者[7,17]。所以下面按体积力失稳建立相关计算模型。

由于互层土中各交互单元层较薄，在武汉地区勘察时并未对其精细分层，往往依据现场及室内试验对其物理力学性质及水文特征采取综合取值。基于此，针对互层土地区基坑突涌分析模型提出以下假设：①互层土层中各分层水头一致；②将互层土层看作均一土层，物理力学指标与勘察报告中综合取值一致。

图4为考虑土体强度时的基坑坑底单元体受力分析图。单位土体的稳定条件如下[18]：

图4 出渗面单位土体受力分析Fig.4 Stress analysis diagram of the unit of the seepage surface

(1)渗透力J=γwi；

(2)土体自重与浮力的合力γ′；

(4)单位土体所受的黏聚力c。

因此坑底互层土层土产生突涌的条件为[18]：

(9)

(10)

(11)

则坑底土体产生突涌渗透破坏的条件为：

i≥ic

(12)

式中：i——坑底互层土层中水力坡降；

ic——土体突涌破坏临界水力坡降；

ξ——坑底互层土侧压力系数。

图5 互层土坑底突涌计算示意图Fig.5 Schematic diagram of calculation at the bottom of foundation pit in interbedded soil

图5为互层土坑底突涌计算简图。由于厚互层土层中赋存有弱承压水，因此在坑底突涌验算中应当考虑其中地下水的影响。在厚互层土内部地下水作用下达到渗透破坏状态的土体中，会形成一定的“流水”和“流砂”通道。同时由于土颗粒受到渗透力的顶托松动，其间的摩擦力及黏聚力将会大大减弱，故在后续的坑底突涌验算中不考虑这部分土体的摩擦阻力及黏聚力的影响，可以增加安全储备。基于此，首先计算由厚互层土内部的地下水作用而达到渗透破坏状态的土体深度，仅考虑上部土体浮重引起的突涌抗力：

(13)

式中：d——互层土中地下水作用下达临界水力梯度土层深度/m；

γ′——坑底互层土平均浮重度/(kN/m3)；

hw——互层土含水层的承压水头/m；

γw——水的重度，取10 kN/m3；

因此在下部砂层高水头渗透力作用下，厚互层土层提供的抗力可看作两部分：①基坑底互层土层总厚度D土体的浮重；②(D-d)厚度互层土层土体间的摩擦阻力及黏聚力。坑底厚互层土层产生突涌渗透破坏的临界条件为：

(14)

式中：D——基坑底互层土的厚度/m；

φ——坑底互层土平均内摩擦角/(°)；

c——坑底互层土平均黏聚力/kPa。

可进一步得到互层土地区基坑突涌计算公式：

(15)

式中：k——坑底抗突涌安全系数。

4 工程案例分析

以武汉华润万象城基坑工程为例，钻孔揭露土层自上而下分布依次为黏土、厚互层土、粉细砂，其中厚互层土物理力学指标如表2所示，厚互层土中承压水头高度在互层土顶部1.0 m处，下部砂层承压水头高度位于厚互层土顶部3.0 m。

将公式(15)与规范[9]及其他文献[17，19～20]所用方法进行比较，计算结果如图6所示。

表2 武汉万象城基坑工程中厚互层土物理力学指标Table 2 Physical and mechanical indexes of interbedded soil in Wuhan Wanxiang Foundation Pit

图6 各种方法计算所得抗突涌安全系数对比图Fig.6 Comparison of anti-surge safety factors calculated by various methods

(1)在考虑厚互层土的土体强度后，坑底抗突涌安全系数为3.5，规范采用的压力平衡法计算安全系数为1.5，本方法约为规范方法的2.2倍。因此按照本方法计算坑底突涌稳定性将比只考虑土体自重更接近工程实际、更经济。

(2)本文计算方法得到的结果与文献[19]及[20]存在较大偏差，主要是计算原理不同。文献[19]针对的是不透水的黏土层，从面积力失稳的角度进行分析，以黏土层部分顶升作为坑底突涌破坏形式，从而推导出考虑黏土强度的突涌计算方法。互层土层垂向上具备弱透水性，在突涌中往往表现为流土、流砂形式的渗透破坏，与黏土层在水压力作用下的发生的顶裂、顶升突涌破坏形式存在明显不同。因此基于不透水层的计算方法不适合于厚互层土。

(3)文献[17]中弱透水层的计算方法与本节提出的方法结果相近。原理上两者相似，均从坑底土突涌渗透破坏的力学机理出发，充分考虑动水压力，即渗透力的影响，建立了基坑抗突涌稳定分析模型。虽然厚互层土层在垂向上呈弱透水性，但是还需考虑到互层土层中赋存的弱承压水对土体突涌稳定的影响，因此本节提出方法的计算结果稍小于文献[17]中计算结果。

5 结论

(1)在合理的简化与假设情况下，将厚互层土含水层看作多个薄层承压含水层，采用压力平衡方法判定突涌不稳定区域。得出在开挖厚互层土上覆黏土层时，突涌不稳定区域仅局限于顶部的1～2 m小范围内，基坑整体处于稳定状态，说明此时可以将厚互层土层看作隔水层。

(2)建立了厚互层土基坑抗突涌稳定分析模型，并提出相应的突涌稳定性安全系数计算公式。结合武汉某深基坑工程，计算出厚互层土突涌稳定性安全系数，与《建筑基坑支护技术规程》和现有文献计算结果进行了对比，得出本方法计算结果是规范法的2.2倍，与现有文献计算结果相近，更符合工程实际，但仍需大量工程实践的检验。