Q-代数上的余核映射

李　瑞

(陕西师范大学 数学与信息科学学院， 陕西 西安　710062)



·数理科学·

Q-代数上的余核映射

李瑞

(陕西师范大学 数学与信息科学学院， 陕西 西安710062)

利用Quantale中余核映射的思想和方法,在Q-代数中引入了Q-代数余核映射的概念,得到了Q-代数余核映射的若干性质,讨论了Q-代数余核映射到单位Q-代数与GirardQ-代数的扩张问题。

Quantale;Q-代数;Q-代数余核映射;GirardQ-代数

Quantale是由Mulvey[1]于1986年在研究非交换C*-代数的谱时首先提出的,其背景是给量子力学提供新的数学模型。由于Quantale自身具有丰富的序结构和代数结构,使得Quantale理论已经应用到C*-代数、线性逻辑、环的理想理论等诸多领域中。

受环上代数结构和结论的启发,文献[2-3]在Quantale和Quantale模的基础上引入了Quantale代数(简称Q-代数)的概念,已成功应用到多值拓扑的研究中[4]。需要指出的是,文献[5]证明了Q-代数范畴同构于模糊Quantale范畴,所以Q-代数可以看成是Quantale模糊化的结构。另外,受Girard quantale和Girard 双模的启发,文献[6]给出了GirardQ-代数的概念,并证明了每个Q-代数都可以嵌入到一个GirardQ-代数中。在Quantale理论中,由于余核映射完全刻画了子Quantale,所以研究余核映射是十分必要的。文献[7]分别研究了余核映射到单位QuantaleQ[e]与Girard quantaleQ×Qop的扩张问题。受此启发,本文在Q-代数中引入了余核映射的概念,考虑了Q-代数余核映射到单位Q-代数与GirardQ-代数的扩张问题。

1　预备知识

在本文中,用0表示完备格中的最小元,1表示完备格中的最大元。

定义1[1]设Q是完备格,&是Q上的二元运算且满足

1) ∀a,b,c∈Q,(a&b)&c=a&(b&c);

2) ∀a∈Q,{bi}i∈I⊆Q,a&(∨i∈Ibi)=∨i∈I(a&bi)且(∨i∈Ibi)&a=∨i∈I(bi&a),则称(Q,&)是Quantale,简称Q是Quantale。

由Quantale的定义知a&-和-&a是Q上的保并映射,所以它们都有右伴随,分别用a→r-和a→l-表示,即∀a,b,c∈Q,a&b≤c⟺a≤b→lc⟺b≤a→rc。

设Q是Quantale。若存在e∈Q使得∀a∈Q,e&a=a&e=a,则称e是Q的单位元,且Q是单位Quantale。若∀a,b∈Q,a&b=b&a,则称Q是交换Quantale。

定义2[1]设Q是Quantale,c,d∈Q。

1) 若∀a∈Q,有a→rc=a→lc,则称c是Q上的循环元。

2) 若∀a∈Q,有(a→rd)→ld=a=(a→ld)→rd,则称d是Q上的对偶元。

3) 若Q中有一个循环对偶元,则称Q是Girardquantale。

定义3[1]设Q1,Q2是Quantale。如果映射f:Q1→Q2满足

1) ∀{ai}i∈I⊆Q1,f(∨i∈Iai)=∨i∈If(ai);

2) ∀a,b∈Q1,f(a&b)=f(a)&f(b),

则称映射f为Quantale同态。

定义4[1]设Q是Quantale。若映射g是Q上的余闭包算子且∀a,b∈Q,g(a)&g(b)≤g(a&b),则称g是Q上的余核映射。

定义5[8]设Q是Quantale,M为完备格。如果映射·:Q×M→M满足

1) ∀{ai}i∈I⊆Q,∀m∈M,(∨i∈Iai)·m=∨i∈I(ai·m);

2) ∀a∈Q,∀{mj}j∈J⊆M,a·(∨j∈Jmj)=∨j∈J(a·mj);

3) ∀a,b∈Q,∀m∈M,(a&b)·m=a·

(b·m),

则称(M,·)是左Q-模。

由左Q-模的定义知a·-和-·m保任意并,所以它们都有右伴随,分别用a|→r-和m|→l-表示,即∀a∈Q,∀m,n∈M,a·m≤n⟺m≤a|→rn⟺a≤m|→ln。若Q是单位Quantale,左Q-模(M,·)满足∀m∈M,eQ·m=m,则称(M,·)是单位左Q-模。对偶地,可定义(单位)右Q-模。我们约定本文中的Q模均为左Q-模。

定义6[8]设(M,·),(N,·)为Q-模。如果映射f:M→N满足

1) ∀{mi}i∈I⊆M,f(∨i∈Imi)=∨i∈If(mi);

2) ∀a∈Q,∀m∈M,f(a·m)=a·f(m),

则称映射f为Q-模同态。

定义7[2]设Q是Quantale。如果三元组(A,·,⊗)满足:

1) (A,·)是Q-模;

2) (A,⊗)是Quantale;

3) ∀q∈Q,a,b∈A,q·(a⊗b)=(q·a)⊗b=a⊗(q·b),

则称(A,·,⊗)为Q-代数。

定义8[6]设(A,·,⊗)为Q-代数。若(A,⊗)是单位Quantale,则称(A,·,⊗)为单位Q-代数。

定义9[9]设(A,·,⊗),(B,·,⊗)是Q-代数。若映射f:A→B既是Quantale同态又是Q-模同态,则称f是Q-代数同态。若f是单射,则称f是Q-代数嵌入。若f还是双射,则称f是Q-代数同构。

定义10[6]设(A,·,⊗)是Q-代数,S⊆A。若S关于任意并,·,⊗运算封闭,则称S是A的子Q-代数。

2　Q-代数余核映射

定义11设(A,·,⊗)是Q-代数。若g是A上的余闭包算子且∀q∈Q,a,b∈A,有g(a)⊗g(b)≤g(a⊗b),q·g(a)≤g(q·a),则称g是Q-代数余核映射。

注1 1) 当Q=2时,Q-代数余核映射恰为Quantale余核映射。

2)用CN(A)表示Q-代数(A,·,⊗)上所有余核映射的全体,则CN(A)关于逐点序是完备格。

命题1设(A,·,⊗)是Q-代数。若g是A上的Q-代数余核映射,则Ag={a∈A|g(a)=a}是A的子Q-代数。反之,若S是A的任意子Q-代数,则存在Q-代数余核映射g,使得S=Ag。

证 明与Quantale情形的证明类似[1]。

命题2设(A,·,⊗)是Q-代数,则∀a∈A,g=a⊗(a→r-):A→A是Q-代数余核映射。

证 明1) g(x)=a⊗(a→rx)≤x。

2)若x≤y,则g(x)=a⊗(a→rx)≤a⊗(a→ry)=g(y)。

3) g(g(x))=g(a⊗(a→rx))=a⊗(a→r(a⊗(a→rx)))=a⊗(a→rx)=g(x)。

4) g(x)⊗g(y)=(a⊗(a→rx))⊗(a⊗(a→ry))≤a⊗((a→rx)⊗y)≤a⊗(a→r(x⊗y))=g(x⊗y)。

5) ∀q∈Q,x∈A,q·g(x)=q·(a⊗(a→rx))=(q·a)⊗(a→rx)=a⊗(q·(a→rx))≤a⊗(a→r(q·x))=g(q·x)。所以g=a⊗(a→r-):A→A是Q-代数余核映射。

命题3设(A,·,⊗)是单位Q-代数,eA是单位元。E(A)={a∈A|a⊗a=a,a≤eA,∀b∈A,a⊗b=b⊗a},则∀a∈E(A),g=-⊗a:A→A是Q-代数余核映射。

证 明1) g(x)=x⊗a≤x⊗eA=x。

2)若x≤y,则g(x)=x⊗a≤y⊗a=g(y)。

3) g(g(x))=g(x⊗a)=(x⊗a)⊗a=x⊗(a⊗a)=x⊗a=g(x)。

4) g(x)⊗g(y)=(x⊗a)⊗(y⊗a)=x⊗(a⊗y)⊗a=x⊗(y⊗a)⊗a=x⊗y⊗(a⊗a)=x⊗y⊗a=g(x⊗y)。

5) ∀q∈Q,x∈A,q·g(x)=q·(x⊗a)=(q·x)⊗a=g(q·x)。

所以g=-⊗a:A→A是Q-代数余核映射。

命题4[10]设Q是Quantale。Q[e]={a∨k:a∈Q,k∈{0,e}},其中e∉Q。Q[e]上的任意并如下定义:0∨e=e

∨i∈I(ai∨ki)=

Q[e]上的&′运算如下定义:

(a∨k′)&′(b∨k″)=

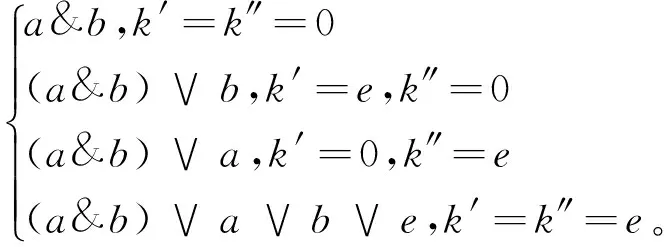
则Q[e]是单位Quantale,其中e是单位元。

定理1[2]1)若(A,·,⊗)是Q-代数,则(A,∘,⊗)是Q[e]-代数且(A,∘)是单位Q[e]-模,其中定义∘:Q[e]×A→A为∀a∨k∈Q[e],m∈A,

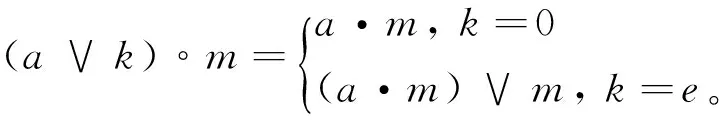
2)若(A,∘,⊗)是Q[e]-代数,则(A,·,⊗)是Q-代数,其中定义·:Q×A→A为∀q∈Q,a∈A,q·a=q∘a。

定理2设A是Q-代数,g是A上的映射,则g是(A,·,⊗)上的Q-代数余核映射当且仅当g是(A,∘,⊗)上的Q[e]-代数余核映射。

证 明充分性:若g是Q[e]代数余核映射,则由定理1显然有g是Q-代数余核映射。

必要性:显然g是QuantaleA上的余核映射且∀q∈Q,x∈A,q·g(x)≤g(q·x)。∀a∨k∈Q[e],x∈A,则

(a∨k)∘g(x)=

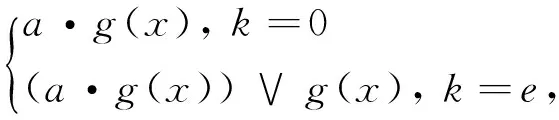
显然,当k=0时,a·g(x)≤g(a·x);当k=e时,a·g(x)≤g(a·x)≤g((a·x)∨x),g(x)≤g((a·x)∨x)。即(a∨k)∘g(x)≤g((a∨k)∘x)。故g是Q[e]-代数余核映射。

设Q是Quantale(A,·,⊗),(B,·,⊗)是Q-代数。定义⊗:(A×B)×(A×B)→A×B为∀(a,b),(c,d)∈A×B,(a,b)⊗(c,d)=(a⊗c,b⊗d);*:Q×(A×B)→A×B为∀q∈Q,(a,b)∈A×B,q*(a,b)=(q·a,q·b)。容易验证(A×B,*,⊗)是Q-代数。

定理3 设Q是Quantale。(A,·,⊗),(B,·,⊗)是Q-代数,gA是A上的Q-代数余核映射,gB是B上的Q-代数余核映射,定义映射gA×B:A×B→A×B为∀(a,b)∈A×B,gA×B(a,b)=(gA(a),gB(b)),则gA×B是A×B上的Q-代数余核映射。

证 明1) ∀(a,b)∈A×B,gA×B(a,b)=(gA(a),gB(b))≤(a,b)。

2) ∀(a,b)≤(c,d),gA×B(a,b)=(gA(a),gB(b))≤(gA(c),gB(d))=gA×B(c,d)。

3) ∀(a,b)∈A×B,gA×B(gA×B(a,b))=

gA×B(gA(a),gB(b))=

(gA(gA(a)),gB(gB(b)))=

(gA(a),gB(b))=gA×B(a,b)。

4) ∀(a,b),(c,d)∈A×B,gA×B(a,b)⊗gA×B(c,d)=(gA(a),gB(b))⊗(gA(c),gB(d))=(gA(a)⊗gA(c),gB(b)⊗gB(d))≤(gA(a⊗c),gB(b⊗d))=gA×B((a,b)⊗(c,d))。

5) ∀q∈Q,(a,b)∈A×B,q*gA×B(a,b)=q*(gA(a),gB(b))=(q·gA(a),q·gB(b))≤(gA(q·a),gB(q·b))=gA×B(q·a,q·b)=gA×B(q*(a,b))。所以gA×B是A×B上的Q-代数余核映射。

3　Q-代数余核映射的扩张

本节主要讨论了Q-代数余核映射到单位Q-代数与GirardQ-代数的扩张问题。我们约定本节中的Q均表示单位交换Quantale。

命题5[6]设(A,·,⊗)是Q-代数。定义⊗:(Q×A)×(Q×A)→Q×A为∀(a,x),(b,y)∈Q×A,(a,x)⊗(b,y)=(a&b,(x⊗y)∨(a·y)∨(b·x));·:Q×(Q×A)→Q×A为∀q∈Q,(a,x)∈Q×A,q·(a,x)=(q&a,q·x),则(Q×A,·,⊗)是单位Q-代数,且有Q-代数嵌入i:A→Q×A为∀a∈A,i(a)=(0,a)。

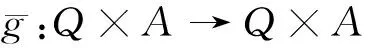
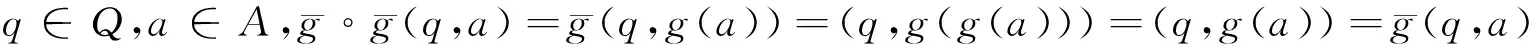
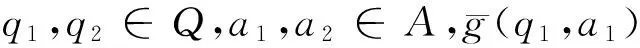
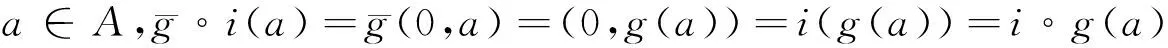
命题6 设(A,·,⊗)是Q-代数,g是Q×A上的Q-代数余核映射,则g|{0}×A是{0}×A上的Q-代数余核映射。

证 明要证g|{0}×A:{0}×A→{0}×A是Q-代数余核映射,∀(0,a)∈{0}×A,由g是Q×A上的Q-代数余核映射知g(0,a)≤(0,a),则g(0,a)∈{0}×A,从而g|{0}×A是{0}×A上的映射。易证g|{0}×A是{0}×A上的Q-代数余核映射。

定义12[6]设(A,·,⊗)是Q-代数,若(A,⊗)是Girardquantale,则(A,·,⊗)是GirardQ-代数。

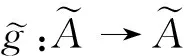
证 明1) ∀a∈A,gp(a)=π1∘g∘ε(a)=π1∘g(a,1)≤π1(a,1)=a。

2)若a≤b,则gp(a)=π1∘g∘ε(a)=π1∘g(a,1)≤π1∘g(b,1)=π1∘g∘ε(b)=gp(b)。

3)设g(a,1)=(c,d),由于g(a,1)≤(a,1),则(c,d)≤(a,1),从而d≥1,即d=1,于是g(a,1)=(c,1)。由g是余核映射知g∘g(a,1)=g(a,1),即g(c,1)=g(a,1)。因此gp(a)=π1∘g∘ε(a)=π1∘g(a,1)=π1∘g(c,1)=gp(c)=gp∘gp(a)。

4) ∀a,b∈A,gp(a)⊗gp(b)=(π1∘g∘ε(a))⊗(π1∘g∘ε(b))=(π1∘g(a,1))⊗(π1∘∘g(b,1))=π1(g(a,1)⊗g(b,1))≤π1(g((a,1)⊗(b,1)))=π1(g(a⊗b,1))=π1∘g∘ε(a⊗b)=gp(a⊗b)。

5) ∀q∈Q,a∈A,由(3)可令g(a,1)=(c,1),则q·g(a,1)=q·(c,1)=(q·c,q|→r1)=(q·c,1)且g(q·(a,1))=g(q·a,q|→r1)=g(q·a,1)。由于q·g(a,1)≤g(q·(a,1)),则q·c≤π1∘g(q·a,1)。因此q·gp(a)=q·π1(g(a,1))=q·π1(c,1)=q·c≤π1∘g(q·a,1)=gp(q·a)。故gp是A上的Q-代数余核映射。

[1]ROSENTHAL K I. Quantales and their Applications[M]. New York: Longman Scientific and Tecnical, 1990.

[2]PAN Fang-fang, HAN Sheng-wei. Free Q-algebras[J]. Fuzzy Sets and Systems, 2014, 247: 138-150.

[3]SOLOVYOV. S A. A representation theorem for quantale algebras[J]. Contributions to General Algebra, 2008, 18: 189-198.

[4]SOLOVYOV. S A. From quantale algebroids to topological spaces: Fixed-and variable-basis approaches[J]. Fuzzy Sets and Systems, 2010, 161: 1270-1287.

[5]汪开云, 赵彬. 模糊Quantale范畴的性质[J]. 陕西师范大学学报: 自然科学版, 2013, 41(3): 1-6.

[6]WANG Kai-yun, ZHAO Bin. On embeddings ofQ-algebras[J]. Houston Journal of Mathematics, 2016, 42(1): 73-90.

[7]HAN Sheng-wei, ZHAO Bin. The quantic conuclei on quantales[J]. Algebra Universalis, 2009, 61: 97-114.

[8]PASEKA J. Quantale Modules[D]. Habilitation thesis, Department of Mathematics, Faculty of Science,Masaryk University,Brno,June 1999.

[9]王蕊, 赵彬. Quantale代数及其代数理想[J]. 模糊系统与数学, 2010, 24(2): 44-49.

[10] HAN Sheng-wei, ZHAO Bin. Remark on the unital quantaleQ[e][J]. Applied Categorical Structures, 2012, 20: 239-250.

(编辑亢小玉)

The conuclei onQ-algebras

LI Rui

(College of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710062， China)

By using the methods and thoughts of conuclei on Quantales, the notion ofQ-algebra conuclei is introduced.Some properties ofQ-algebra conuclei are obtained.The extensions ofQ-algebra conuclei to unitalQ-algebra and GirardQ-algebra are discussed.

Quantale;Q-algebra;Q-algebra conuclei; GirardQ-algebra

2015-04-11

国家自然科学基金资助项目(11171196,11301316);中央高校基本科研业务费专项基金资助项目(GK201501001)

李瑞，女，山西运城人，从事格上拓扑与非经典数理逻辑研究。

O153.1

A

10.16152/j.cnki.xdxbzr.2016-02-003