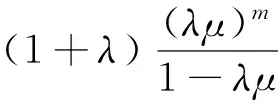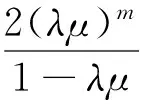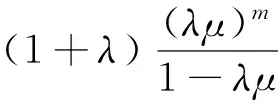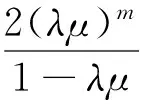锥Banach空间中多个自映射的公共不动点定理

张　弘，薛西锋

(西北大学 数学系, 陕西 西安　710127)



·数理科学·

锥Banach空间中多个自映射的公共不动点定理

张弘，薛西锋

(西北大学 数学系, 陕西 西安710127)

研究在锥Banach空间中，多个弱相容的自映射在满足特定压缩条件下，通过构造迭代序列，并证明序列收敛性，得到此类算子具有唯一的公共不动点，丰富了压缩映像的不动点理论。

锥Banach空间； 锥赋范空间； 弱相容； 公共不动点； 叠合点

1922年,Banach提出著名的压缩映像原理[1],后来很多学者给出多种压缩映像,并证明了压缩映像不动点理论。1996年,Junck定义了两个自映射弱相容的概念[2],2006年,Junck和Rhoades证明了在度量空间中,两个弱相容的自映射存在公共不动点[3]。2007年黄龙光和张宪在文献[4]中用序Banach空间取代实数,引入锥度量空间,讨论了序列的收敛性,并证明在完备的锥度量空间中算子T:X→X在满足某些特定压缩条件下,存在唯一的不动点。后来,一些学者通过省略正规锥的条件[5]或去掉映射连续性的条件[6],证明锥度量空间中的不动点存在性理论。文献[7-14]都证明了锥度量空间中多个弱相容的自映射存在公共不动点的理论。这些成果都更加丰富了锥度量空间中的不动点理论。近些年,许多学者将锥度量空间中的不动点理论推广到锥Banach空间[15-17]。如E.karaplnar证明了锥Banach空间中,设d:X×X→E,令d(x,y)=‖x-y‖p,若T:C→C(C⊂E)满足ad(Tx,Ty)+b(d(x,Ty)+d(y,Ty))≤sd(x,y), x, y∈C,则T至少存在一个不动点。本文研究了在锥Banach空间中两个和三个自映射满足给定的压缩条件下, 存在唯一的公共不动点,其结果发展和推广了前人的成果。

1　预备知识

定义1[4]设E是实的Banach空间,P1是E的子集, 当P1满足下列条件,称P1为锥

(i)P1是非空闭集, 且P1≠{0};

(ii)a,b∈R,a,b≥0,x,y∈P1⟹ax+by∈P1;

(iii)P1∩(-P1)={0}。

给定锥P1⊂E,由锥P1可导出E中的偏序关系“≤”,“<”,“≪”。x,y∈E, x≤ y表示y-x∈P1;x

如果存在常数N>0,对任意的x, y∈E,使得θ ≤ x ≤ y⟹‖x‖≤N‖y‖则称P1为正规锥,称满足该不等式的最小常数N为P1的正规常数。

定义2[4]设X为非空集合, d:X×X→E, 满足下列条件:

(i)∀x, y∈X, d (x, y) ≥0, d(x, y)=0⟺x=y;

(ii)∀x, y∈X, d (x,y)=d (y, x);

(iii)∀x, y, z∈X,d(x,y)≤d(x,z)+d(y,z)，

则称d为X上的一个锥度量或者锥距离,(X, d)为锥度量空间或者锥距离空间。

定理1[4]设(X,d)是锥度量空间,且{xn}是X中的序列,P是具有正规常数K的正规锥,{xn}是Cauchy列当且仅当d(xn,xm)→0(m,n→∞)。

定义3[18]设X是R上的向量空间,设映射‖·‖p:X→E满足:

(a)∀x∈X,‖x‖P> 0;

(b)‖x‖P=0⟺x=0;

(c)∀x, y∈X,‖x+y‖P≤‖x‖P+‖y‖P;

(d)∀k∈R,‖kx‖P=|k|‖x‖P，

则称‖·‖P是X的锥范数,(X,‖·‖P)称作锥赋范空间。

每个锥赋范空间都是锥度量空间,d(x,y)=‖x-y‖p。

定义4[19]设(X,‖·‖P)是锥赋范空间, x∈X且{xn}n ≥1⊆X,

(ii)若对任意的c∈E且c≫0,存在N,使得对任意m,n≥N,都有‖xm-xn‖P≤c,则{xn}n ≥1称为X中的Cauchy列;

(iii)若每一个Cauchy列都是收敛的,则(X,‖·‖P)称作完备的锥赋范空间。

完备的锥赋范空间称作锥Banach空间。

引理1[18]设(X,‖·‖P)是锥赋范空间,P是具有正规常数K的正规锥,{xn}⊂X,则

(i){xn}→x当且仅当‖xn-x‖P→0(n→∞);

(ii){xn}是Cauchy列当且仅当‖xn-xm‖P→0(m, n→∞);

(iii){xn}→x,{yn}→y,则‖xn-yn‖P→‖x-y‖P。

定义5[19]设X是非空集合,映射f,g:X→X,若存在x∈X使得w=fx=gx,则称w∈X是f和g的叠合点。

定理2[20]设X是非空集合, 映射f, g:X→X称为弱相容的,对任意u∈X,如果fu=gu,都有fgu=gfu成立。

定理3[21]设X是非空集合, 映射f, g:X→X弱相容,若f和g有唯一的叠合点, 即w=fx=gx,则w是f和g的唯一公共不动点。

2　主要结果

定理4设C是锥Banach空间X的凸闭集, P是具有正规常数K的正规锥,‖x‖P是C在X上的锥范数, d:X×X→E,d(x,y)=‖x-y‖p,映射f, g:C→C满足对任意的x, y∈C有‖fx-fy‖≤α(‖gx-fy‖+‖gy-fx‖)+γ‖gx-gy‖成立。其中α,γ∈[0,1)且2α+γ<1,假设f(X)⊆g(X),g(X)是X的完备子空间, f, g连续且弱相容,则它们有唯一的公共不动点。

证 明设x0为X中任意一点,因为f(x0)∈f(X)⊆g(X),所以存在x1∈X满足f(x0)=g(x1),令y1=f (x0)=g(x1),又f(x1)∈f(X)⊆g(X),所以存在x2∈X满足f(x1)=g(x2),令y2=f(x1)=g(x2),依此类推,得到{yn}⊂X,有yn=f (xn-1)=g(xn)(n=0,1,2,…)。

‖yn-yn-1‖=‖fxn-1-fxn-2‖≤

α(‖gxn-1-fxn-2‖+‖gxn-2-fxn-1‖)+

γ‖gxn-1-gxn-2‖=

α (‖yn-1-yn-1‖+‖yn-2-yn‖)+

γ‖yn-1-yn-2‖≤

α‖yn-yn-1‖+α‖yn-1-yn-2‖+

γ‖yn-1-yn-2‖，

‖yn-yn-1‖≤λ‖yn-1-yn-2‖≤

λ2‖yn-2-yn-3‖≤…≤λn-1‖y1-y0‖，

对任意的m,n且m

‖yn-ym‖≤‖yn-yn-1‖+

‖yn-1-yn-2‖+…+

‖ym+1-ym‖≤

(λn-1+λn-2+…+λm)‖y1-y0‖≤

因为f, g是连续的, 所以f2(xn)→f (z), g2(xn)→g (z), gf (xn)→g (z), fg (xn)→

f(z)

下面证f (z)=g(z)

‖f2(xn)-gf (xn)‖=

‖f2(xn)-fg (xn)‖≤

α(‖gf (xn)-fg (xn)‖+

‖g2(xn)-f2(xn)‖)+

γ‖gf (xn)-g2(xn)‖=

α‖g2(xn)-f2(xn)‖+

γ‖gf (xn)-g2(xn)‖。

令n→∞,得到‖f (z)-g(z)‖≤α‖g (z)-f (z)‖+γ‖g(z)-g (z)‖，所以(1-α)‖f (z)-g(z)‖≤0,因为1-α>0, 所以‖f (z)-g(z)‖=0, 所以f (z)=g(z),所以z是f和g的叠合点。

下面证明唯一性。

假设z1是f, g的另一个叠合点, f (z1)=g(z1)。

‖f (z)-f (z1)‖≤

α(‖g (z)-f (z1)‖+‖g(z1)-f (z)‖)+

γ‖g(z)-g(z1)‖=α(‖f (z)-f (z1)‖+

‖f (z1)-f (z)‖)+γ‖f (z)-f(z1)‖。

因为1-2α-γ>, 所以‖f (z)-f (z1)‖=0, 所以f (z1)=g(z1), 所以f (z)=g(z)=

f (z1)=g(z1)，所以z是f, g的唯一叠合点。

又因为f, g是弱相容的,由定理3知, z是f, g的唯一公共不动点。

推论1设C是锥Banach空间的凸闭集,P是具有正规常数M的正规锥,‖·‖P是C在X上的锥范数d:X×X→E, d(x,y)=‖x-y‖p, 映射f, g:C→C满足对任意x, y∈C，‖fx-fy‖≤α‖gx-fy‖+β‖gy-fx‖+γ‖gx-gy‖成立。其中α, β,γ∈[0,1)且α+β+γ<1,假设f(X)⊆g(X), g(X)是X的完备子空间, f, g连续且弱相容,则f, g具有唯一的公共不动点。

引理2设X是非空集合, f, g, T是X中的自映射,v是它们的叠合点, 若(f, T)弱相容,(g,T)弱相容,则f, g,T具有唯一的公共不动点。

证 明因为v是f,g,T的叠合点,所以fu=gu=Tu,u∈X,因为(f,T)是弱相容的,则fv=fTu=Tfu=Tv,(g,T)是弱相容的, gv=gTu=Tgu=Tv,所以fv=gv=Tv=w,所以w是f, g,T的叠合点,v=w,因为叠合点唯一, 所以v是f,g,T的的唯一公共不动点。

定理5设C是锥Banach空间的凸闭集,P是具有正规常数M的正规锥,‖·‖P是C的锥范数, d:X×X→E, d(x,y)=‖x-y‖p, 映射f, g,T:C→C满足对任意x,y∈C都有‖fx-gy‖≤α‖Tx-fx‖+β‖Ty-gy‖+γ‖Tx-Ty‖。其中α+β+γ<1, 假设f (X)∪g(X)⊆T(X), T(X)是X的完备子空间, 且(f,T)弱相容,(g, T)弱相容,则f, g, T具有唯一公共不动点。

证 明对∀x0∈X, 因为 f (x0)∈f(X)⊆T(X), 所以存在x1∈X, 使得Tx1=fx0, 对∀x1∈X, 因为g(x1)∈g(X)⊆T(X), 所以存在x2∈X, 使得Tx2=gx1, 依此类推, 得到Tx2k+1=fx2k, Tx2k+2=gx2k+1, {Txn}是以x0为初始点的序列。

‖Tx2k+1-Tx2k+2‖=‖fx2k-gx2k+1‖≤

α‖Tx2k-fx2k‖+β‖Tx2k+1-

gx2k+1‖+γ‖Tx2k-Tx2k+1‖≤

(α+γ)‖Tx2k-Tx2k+1‖+

β‖Tx2k+1-Tx2k+2‖，

所以

(1-β)‖Tx2k+1-Tx2k+2‖≤

(α+γ)‖Tx2k-Tx2k+1‖，

所以

‖Tx2k+1-Tx2k+2‖≤

‖Tx2k+2-Tx2k+3‖=

‖gx2k+1-fx2k+2‖=

‖fx2k+2-gx2k+1‖≤

α‖Tx2k+2-fx2k+2‖+

β‖Tx2k+1-gx2k+1‖+

γ‖ Tx2k+2-Tx2k+1‖=

α‖Tx2k+2-Tx2k+3‖+

β‖Tx2k+1-Tx2k+2‖+

γ‖Tx2k+1-Tx2k+2‖，

所以‖Tx2k+2-Tx2k+3‖≤

所以对每一个k=0,1,2,…，有

‖Tx2k+1-Tx2k+2‖≤

而

‖Tx2k+2-Tx2k+3‖≤

‖Tx2m+1-Tx2n+1‖≤

‖Tx2m+1-Tx2m+2‖+

‖Tx2m+2-Tx2m+3‖+…+

‖Tx2n-1-Tx2n‖+‖Tx2n-Tx2n+1‖≤

同理

‖Tx2m-Tx2n+1‖≤

‖Tx2m-Tx2n‖≤

‖Tx2m+1-Tx2n‖≤

所以对所有的0< m< n，

因为P是正规锥,所以

‖Txn-Txm‖≤

所以{Txn}是Cauchy列。

因为T(X)是完备的子空间, 则存在u,v∈X, 使得Txn→v=Tu,

‖Tu-fu‖≤

‖Tu-Tx2n‖+‖Tx2n-fu‖≤

‖v-Tx2n‖+‖fu-gx2n-1‖≤

‖v-Tx2n‖+α‖Tu-fu‖+

β‖Tx2n-1-gx2n-1‖+γ‖Tu-Tx2n-1‖，

所以

‖Tu-fu‖≤

γ‖Tu-Tx2n-1‖)=

γ‖v-Tx2n-1‖)。

同理可证Tu=gu。

下证唯一性。

假设v*是f,g,T的另一个叠合点v*=fu*=gu*=Tu*, u*∈X,‖v-v*‖=‖fu-gu*‖≤α‖Tu-fu‖+β‖Tu*-gu*‖+γ‖Tu-Tu*‖≤γ‖Tu-Tu*‖, 所以v=v*因为(f, T)弱相容, (g, T)弱相容, 由引理2知v是f, g, T的唯一公共不动点。

[1]BANACH S. Sur les opération dans les ensembles abstraits etleur application auxéquations intégrales[J].Fundamenta Math,1922,13:133-181.

[2]JUNGCK G.Common fixed points for noncontinuous nonself maps on nonmetric spaces[J].Far East J Math Sci,1996,4(2):199-215.

[9]UNGCK G, RHOADES B E.Fixed point theorems for occasionally weakly compatible mappings[J].Fixed Point Theory,2006,7(2):287-296.

[4]HUANG L G, ZHANG X. Cone metric spaces and fixed point theorems of contractive mapping[J].J Math Anal Appl,2007,332(2):1468-1476.

[5]REZAPOUR S H, HAMLBARANI R. Some notes on the paper "Cone metric space and fixed point theorems of contravtive mapping" mapping[J]. J Math Anal Appl,2008,345:719-724.

[6]ABBS M, JUNGCK G.Common fixed point results for noncommuting mappings without continuity in cone metric space[J].J Math Anal Appl,2008,341:416-420.

[7]CHOUDHURY B S, METIYA N. The point of coincidence and common fixed point for a pair of mappings in Cone me-tric spaces[J].Comput Math Appl,2010,60(6):1686-1695.

[8]BARI C D, VETRO P.Common fixed points in cone metr-ic space for MK-pairs and L-pairs[J].Ars Comb,2011,99:429-437.

[9]BARI C D, SAADATI R, VETRO P. Common fixed points in cone metric spaces for CJM-pair[J].Math Comput Modelling,2011,54(9-10):2348-2354.

[10] VETRO P. Common fixed points in cone metric spaces[J].Rend Circ Mat Palermo, 2007,56(3):464-468.

[11] KARAPINAR E. Couple fixed point on cone metric spaces[J].Gazi University Journal of Science,2011,24(1):51-58.

[12] PRUDHVI K. Common fixed points in cone metric spaces[J].American Journal of Mathematical Analysis,2013,1(2):25-27.

[13] RADENOVIC S. Common fixed points under contractive conditions in cone metric spaces[J].Computers and Mathematics with Applications,2009,58:1273-1278.

[14] ALTUN I,DURMAZ G. Some fixed point theorems on ordered cone metric spaces[J].Rend Circ Mat Palermo,2009,58:511-515.

[15] KARAPINAR E. Some fixed point theorems on the cone Banach space,Proc[C]∥7 ISAAC Congress,World Scientific,2011:606-612.

[16] TURKOGLU D, ABULOHA M, ABDELJAWAD T.Some theorems and examples of cone Banach spaces[J].J Comput Anal Appl,2010,12(4):739-753.

[17] VARGHESE P G, DERSANAMBIKA K S. Common fixed point theorem on cone Banach space[J].Kathmandu University Journal of Science Engineering and Technology,2013,9(1):127-133.

[18] KARAPINAR E. Fixed point theorems in cone Banach space[J].Fixed Point Theory and Application,2009，609281：1-9.

[19] MALVIYA N. Proving Fixed Point Theorems Using General Principles in cone Banach spaces[J].International Mathematical Forum,2011,6(3):115-123.

[20] JHA K. A common fixed theorem in a cone metric space.Kathmandu University Journal of Science[J].Engineering and Technology,2009,5(1):1-5.

[21] JUNGCK G, RHOADES B E. Fixed point for set valued functions without continuity[J].Indian J Pure Appl Math,1998,29(3):227-238.

(编辑亢小玉)

Common fixed point of several self-mappings in cone Banach space

ZHANG Hong， XUE Xi-feng

(Department of Mathematics, Northwest University, Xi′an 710127， China)

The aim of this paper is to study several weakly compatible mappings in cone Banach space, satisfying some certain contractive conditions,with establishing iterative sequence and proving the sequence to converge. Several weakly compatible self-mappings have the unique common fixed point. The results extend the known achievements and make them have a rich application.

cone Banach space; cone normed space; weakly compatible mappings; common fixed point; coincidence point

2015-10-10

陕西省自然科学基金资助项目(2012JM1017)

张弘，女，陕西渭南人，从事非线性泛函分析研究。

薛西锋，男，陕西渭南人，西北大学教授，从事非线性泛函分析研究。

O177.91

A

10.16152/j.cnki.xdxbzr.2016-02-001