基于残余应力分析的加工中心定位精度保持性研究

马文硕　米　洁　杨庆东

北京信息科技大学，北京，100192



基于残余应力分析的加工中心定位精度保持性研究

马文硕米洁杨庆东

北京信息科技大学，北京，100192

基于残余应力分析对加工中心的定位精度保持性进行了研究，提出一种考虑残余应力影响的定位误差分析方法。首先分析了产生残余应力的主要制造工艺环节，采用有限元法对国内某机匣加工中心床身进行了残余应力分析，得出了该床身在铸造与机械加工环节后的残余应力大小及分布情况。在此基础上对残余应力释放后床身-导轨安装基面的变形进行了预测。通过与试验数据的对比，验证了有限元建模的可信性。最后对残余应力释放引起的导轨定位误差进行了计算。

导轨定位精度；残余应力；精度保持性；有限元

0　引言

机床的基础件随时间缓慢变形是影响国产数控机床精度保持性的重要因素，而导致基础件变形的主要因素是残余内应力的释放。国外机床厂家在20世纪80年代生产的高端机床可以在10年内保持其定位精度[1]，而当前国内精密机床的精度保持时间仍远低于国外上世纪80年代水平[2]。

国内外学者已经对残余应力的理论预测与测试方法进行了较多的研究[3-5]。在机床领域，Palumbo等[6]建立了能够准确模拟铸造过程并预测铸造残余应力的有限元模型；胡敏等[7]对某卧式加工中心床身的精度保持性进行了研究，认为铸造残余应力及其不充分消除是导致床身精度保持性差的主要因素；黄微等[8]对机械加工后的导轨变形状况进行了监测，获得了导轨随残余应力释放的精度衰退总体情况。但目前鲜有学者对机床因残余应力释放而导致的定位精度下降进行定量研究。

为从根本上提高机床精度保持性并探究残余应力对定位精度的影响，必须对残余应力释放后基础件的变形进行定量计算。本文提出一种基于残余应力分析的定位误差分析方法，通过有限元法定量分析了残余应力对定位精度的影响，并通过实验验证了该有限元模型的可信性。

1　残余应力的产生及其对定位精度的影响

残余应力引起的导轨直线度误差是使数控机床精度变差的主要原因之一。机床基础件经铸造、机械加工等工序后，其存有的残余内应力会在未经完全消除的情况下随着时间的延长而不断释放，使导轨安装基面发生弧面弯曲，继而使导轨与床身的结合部发生变形，产生直线度误差。

如图1所示，基础件在铸造、机械加工、焊接等环节均会产生残余应力，且大部分残余应力产生自铸造与机械加工环节。其中在机械加工环节，随着被切削材料的去除，一方面由于原残余应力场的重新分布使加工面产生变形，另一方面因刀具挤压及摩擦，在已加工表面引入了新的切削残余应力。但由于后者只分布于工件表层[9]，故其对机床精度的影响可忽略不计。

图1　残余应力产生环节

据此，本文以国内某机匣加工中心床身为分析对象，提出依据残余应力分析结果预测机床定位误差的方法，具体如下：首先针对铸造、机械加工两个对残余应力的产生起主导作用的工艺环节，对床身进行铸造残余应力仿真分析；然后基于该分析，对应力释放后的床身变形进行预测；最后计算出在螺栓预紧力下导轨的定位误差。

2　导轨安装基面残余应力分布及释放分析

床身结构如图2所示，因工作台位于其x轴之上，故只考虑在残余应力释放后x方向床身-导轨安装基面沿其长度方向的直线度误差，利用ABAQUS6.13有限元分析软件，分别对床身进行铸造残余应力与残余应力释放分析。

图2　机匣加工中心床身

2.1铸造残余应力分析

为尽可能减小计算量并突出问题实质，对铸造过程按下述假设进行简化处理：①采用接触单元法对铸件砂型边界进行简化处理；②铸件无初始内应力；③不考虑铸件的浇注过程。

床身铸造的工艺条件为：砂型铸造，浇铸温度为1400 ℃，72h后落砂，自然冷却。

采用顺序热耦合的方法进行传热和应力场分析，主要分析过程如图3所示，在进行传热分析后，再将该分析结果作为热载荷进行铸造残余应力分析。

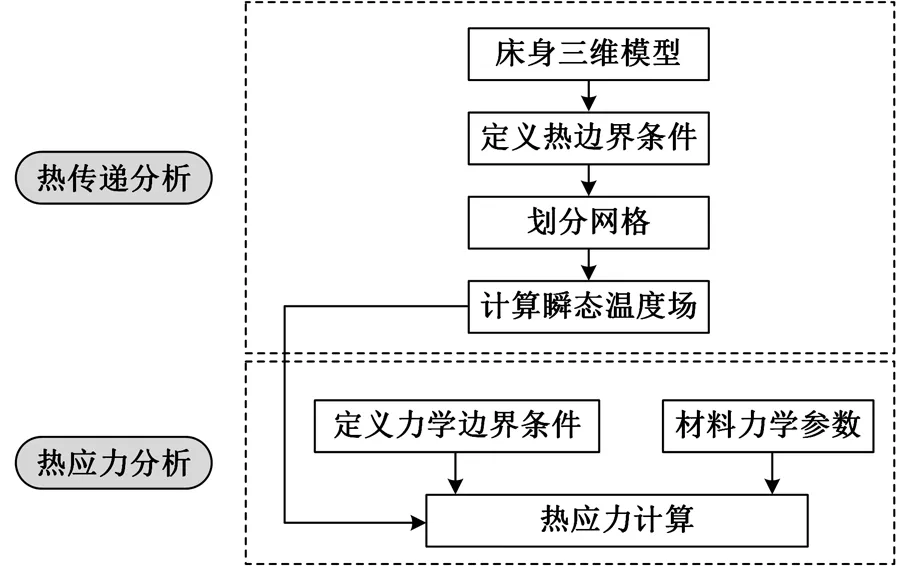
图3　有限元分析流程图

2.1.1建立材料本构模型

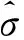
式中，I1为应力第一不变量；J2为偏应力第二不变量；θ为Lode角。

用主应力表示为

S1=cosθS2=cos(θ-2π/3)

S3=cos(θ+2π/3)

式中，σ1、σ2、σ3分别为第一、第二、第三主应力。

2.1.2仿真结果分析

因灰铸铁的弹塑性转变温度范围为350～450 ℃，认为温度在该区间内时的残余应力即为铸造残余应力，故截取导轨安装基面温度在该区间内时床身温度的分布情况。由图4a可知，在29h的冷却过程中，床身T字形中部冷却最慢，与边缘形成较大温度差。图4b所示为床身铸造应力分布情况，壁厚差较大处与筋板尖角处均存在应力集中，表层或薄壁处呈残余压应力，内层与厚壁处呈残余拉应力，在实际生产中铸造残余拉应力易造成裂纹现象。

图5为床身中部筋板的实物图，由于受到残余拉应力影响，筋板呈颈缩状，易产生裂纹，这与分析结果相符。

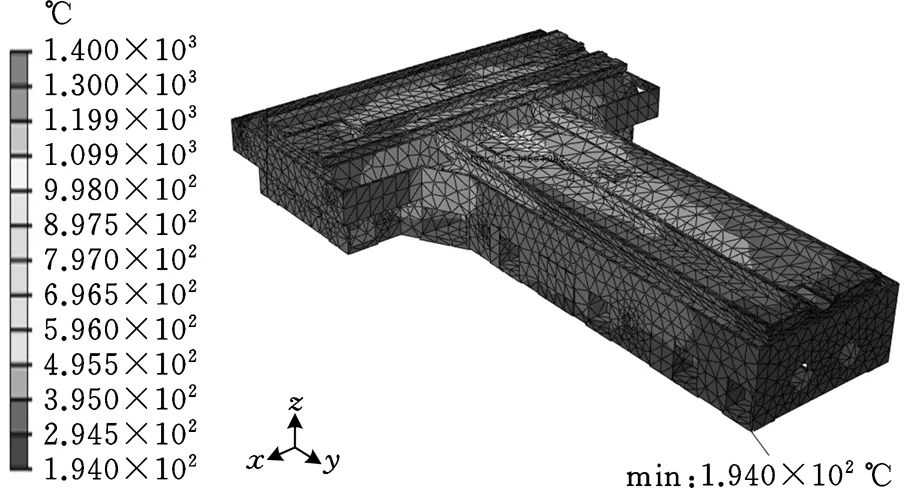
(a)床身温度场

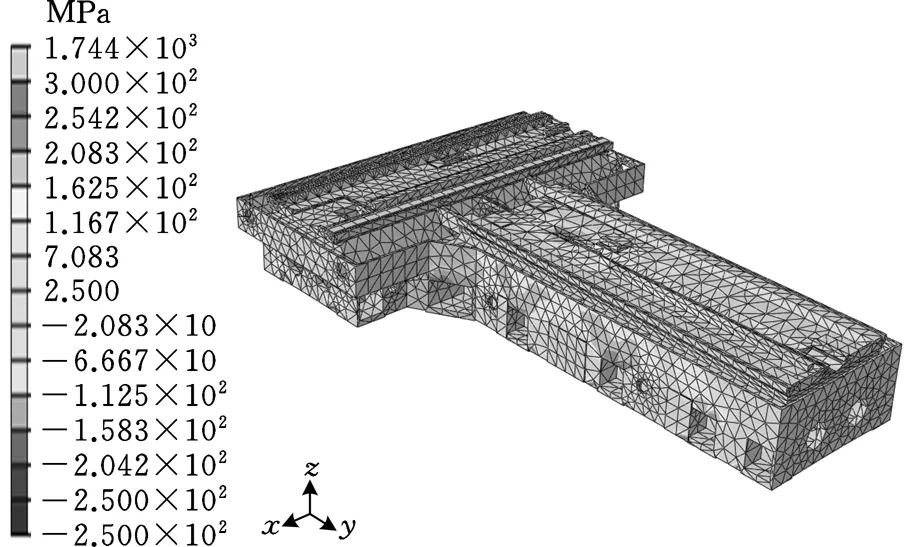
(b)床身铸造应力云图图4　铸造残余应力分析结果

图5　床身中部筋板实物图

因x轴导轨安装基面的长度远大于其宽度与高度，冷却时其收缩方向与残余应力均以x方向为主，此时可以近似认为该处的应力分布为平面应力状态。图6所示为x轴导轨的安装基面沿长度方向的最大主应力曲线，其中部呈残余压应力，最大主应力绝对值在80MPa左右波动，且呈现出中间高两边低的分布态势。其原因为：床身在冷却过程中，其中部收缩速度明显大于两端，受到两端的牵制，从而使中部受压应力。随着中部与两端降温梯度的增大，二者应力的绝对值差也相应增大。

2.2剥层引起的残余应力释放分析

床身经机械加工后，残余应力的重新分布与释放，使x轴导轨安装基面沿其长度方向产生变形。分析以较为精准地获取该变形为目的，将铸造残余应力场作为初始载荷施加于床身上，采用剥层法模拟去除材料过程。随着每层材料的去除，床身初始残余应力场的平衡状态被破坏，不断发生重分布，使导轨安装面变形，最终导致紧固其上的导轨下沉。根据实际机械加工工艺参数及加工余量，将床身毛坯的导轨安装基面沿厚度方向分割为10层，每层厚1mm，每个分析步去除1层，以模拟实际走刀过程。

图7所示为每层材料剥除并使残余应力达到新平衡后x轴导轨安装基面的挠曲线。变形呈下凹状(最凹处曲线由上至下依次为第1～10层材料去除后导轨安装基面的变形)，且随着剥层深度的增加而增加，从第1层材料剥除后的9μm左右增加至第10层材料剥除后的16μm左右。

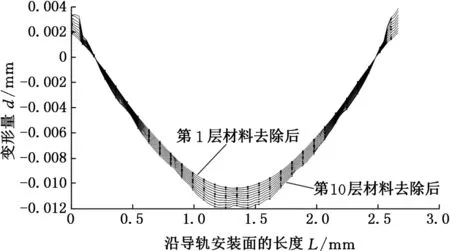
图7　不同剥层深度下导轨安装基面的变形

材料去除后残余应力与曲率变化的理论关系式为

(1)

式中，Ri+1、Ri+2分别为第i+1层材料去除前后工件中性面的曲率半径；hi+1、hi+2分别为第i+1层材料去除前后工件高度；σi+1为构件初始状态时第i+1层的残余应力值；t为剥除材料厚度；E为弹性模量；Ski为原始构件去除了k层材料后第i+1层的残余应力校正项。

对式(1)等号两边进行积分可得挠度变化关系式：

wi+1(x)-wi+2(x)=

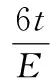
(2)

i≥1

式(2)表明，有限元分析结果与理论公式所预测趋势一致，并可得出结论：床身毛坯的铸造残余应力分布规律对床身导轨安装基面的变形具有重要影响。导轨安装基面的厚度与其挠度的绝对值呈正比，且材料去除率越大，变形挠度越大。

3　导轨安装基面变形的试验验证

采用TaylorHobsonUltra高精度自准直仪，对床身x轴导轨安装基面沿长度方向的直线度进行测量。考虑实际现场测试条件限制，为使仿真条件与实际情况一致，将测试时间安排为：床身精加工后半个月进行第一次测量，然后将床身置于恒温车间7个月，待残余应力基本释放完毕后进行第二次测量。测量结果见图8。

图8　直线度误差测量结果

由图8可见，床身在精加工后的半个月时间里，在x轴理论行程内的导轨安装基面直线度误差约为5μm。再经7个月的放置后，床身残余应力已基本释放完毕，导轨安装基面呈下凹状，此时直线度误差约为16.67μm。对比仿真结果与试验结果，可以认为二者基本吻合，说明采用上述建模方法所得结果是可信的。

4　导轨定位误差计算

根据国际ISO230标准，定位误差包括：系统定位误差、重复定位误差及反向间隙。其中，系统误差约占定位误差的一半。本文对导轨安装基面残余应力释放引起的系统定位误差进行计算。

采用M12螺钉对变形的导轨安装基面与导轨进行装配。定义二者与螺钉的接触后对螺钉施加大小为38.4kN的标准预紧力。根据x轴导轨的理论行程，截取导轨中段长为1400mm的部分进行定位误差分析。根据图9所示数据，导轨在理论行程内的直线度误差h=8.423μm。

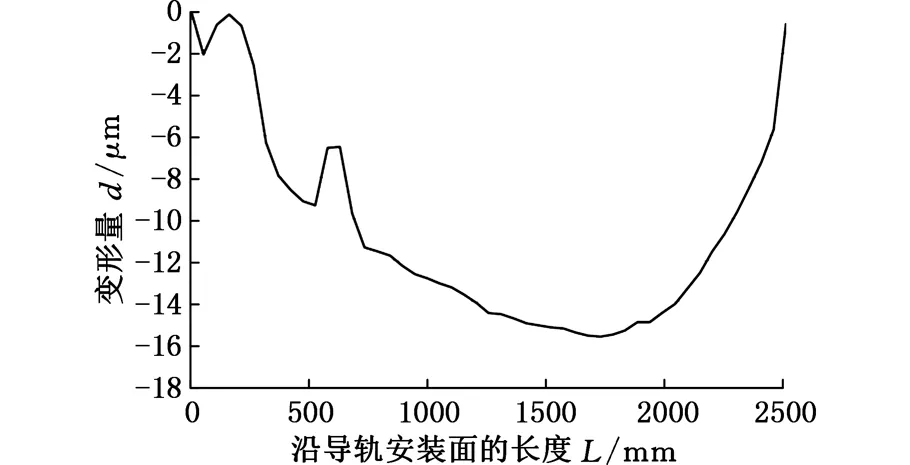
图9　导轨变形曲线

导轨直线度误差的几何模型如图10所示，当导轨处于理想情况下，即不存在直线度误差时，滑块的实际行程s′和预先设定的行程s相等，此时有s=s′；导轨存在直线度误差时，滑块的移动轨迹出现了偏角α，这时s≠s′。

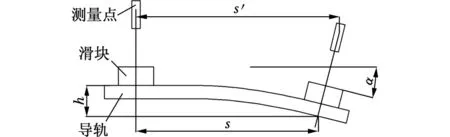
图10　导轨直线度误差几何模型

已知测量点至导轨面的距离H=405mm，x轴导轨的理论行程s=1400mm，此时可得定位误差[12]

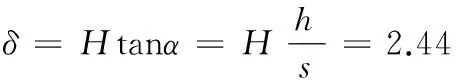
结果表明，基础件的残余应力分布主要取决于铸造残余应力；床身与导轨结合部的变形取决于导轨安装面的材料去除率。对于该加工中心，其设计定位精度要求为6μm。在前述制造加工工艺条件下，由残余应力引起的导轨直线度误差为2.44μm，约占其系统定位误差的80%。该结果对于同类机床精度保持性的研究，具有一定参考价值。

5　结论

(1)采用有限元分析法模拟了国内某加工中心床身在铸造及机械加工环节产生的残余应力分布情况，认为床身的残余应力主要由铸造环节产生，并在机械加工环节随着应力的释放而发生变形，且变形挠度随着材料去除率的增大而增大。仿真结果与实测数据基本吻合，验证了有限元模型的可信性。

(2)x轴导轨由内应力释放所引起的定位误差为2.44μm，虽尚处于误差范围要求的6μm之内，但考虑到仍存在重复定位误差与反向间隙以及机床运行后精度退化等因素，宜进一步研究时效规范和导轨加工工艺以提高机床的精度保持性。

(3)对于小型机床或精度要求较低的机床，残余应力对加工精度产生的影响较小；对于大型机床与高精度的加工中心，若要进一步提高加工精度及其精度保持性，则必须考虑基础件残余应力释放对定位误差产生的影响。

[1]刘称意. 考虑导轨结合面影响的数控机床动态特性分析及结构优化[D].沈阳: 东北大学, 2010.

[2]马军旭, 赵万华, 张根保. 国产数控机床精度保持性分析及研究现状[J].中国机械工程,2015, 26(22)：3108-3115.

Ma Junxu, Zhao Wanhua, Zhang Genbao. Research Status and Analyses on Accuracy Retentivity of Domestic CNC Machine Tools[J]. China Mechanical Engineering, 2015, 26(22)：3108-3115.

[3]Shin S H. Prediction of the Dimensional Instability Resulting from Machining of Residually Stressed Components[D]. Lubbok: Taxas Tech Universi-ty, 1995.

[4]Li J L, Jing L L, Chen M. An FEM Study on Residual Stresses Induced by High-speed End-milling of Hardened Steel SKD11[J]. Journal of Materials Processing Technology, 2009, 209(9): 4515-4520.

[5]王秋成. 航空铝合金残余应力消除及评估技术研究 [D]. 杭州: 浙江大学, 2003.

[6]Palumbo G, Piccininni A, Piglionico V, et al. Modelling Residual Stresses in Sand-cast Superduplex Stainless Steel[J]. Journal of Materials Processing Technology, 2015, 217: 253-261.

[7]胡敏, 余常武, 赵万华, 等. 机床基础大件振动时效工艺参数优化方法[J]. 中国机械工程, 2014,25(23): 3137-3142.

Hu Min, Yu Changwu, Zhao Wanhua. Optimiza-tion Method of VSR Process Parameters for Large Machine Tool Body[J]. China Mechanical Engineering, 2014, 25(23): 3137-3142.

[8]黄微, 陈艳丽. 机械加工后铸件应力与变形的试验研究[J]. 铸造技术, 2002, 23(2): 89-91.

Huang Wei, ChenYanli. Experimental Investigation of Stress and Deformation of Casting after Machining[J]. Foundry Technology, 2002, 23(2): 89-91.

[9]苗勇. 残余应力对整体结构件加工变形的影响[J]. 组合机床与自动化加工技术, 2011(9): 81-83.

Miao Yong.The Influence of Residual Stress on the Machining Distortion of Monolithic Component[J]. Modular Machine Tool and Automatic Manu-facturing Technique, 2011(9): 81-83.

[10]程永周. CK61125 车床床身振动时效机理及工艺研究 [D]. 洛阳：河南科技大学, 2011.

[11]赵明. 大型铣床床身铸造过程模拟仿真及工艺优化[D].淄博：山东理工大学, 2014.

[12]王林艳, 杨永智. 机床导轨直线度误差对定位精度的影响分析[J]. 金属加工: 冷加工, 2014(2): 68-69.

Wang Linyan, Yang Yongzhi. Analysis of Inf-luence of Machine Tool Guide Rail’s Straightness Error on Positioning Precision[J]. Machinist Metal Cutting, 2014(2): 68-69.

(编辑卢湘帆)

Research on Positioning Accuracy Retentivity of Machining Center Based on Residual Stress

Ma WenshuoMi JieYang Qingdong

Beijing Information Science & Technology University,Beijing,100192

The relationship between residual stress and the positioning accuracy retentivity of machining center was conducted. Then a new method for quantitative analysis of positioning errors caused by residual stress was proposed. Following the analyses of the processes which produced residual stress, residual stress analyses were carried out on a domestic cartridge receiver machining center bed by using finite element method. Thus the distribution of the residual stress of the bed after casting process and machining process was obtained. Then the deformation of the joint surface between the bed and guide was predicted, which was verified by being compared with the actual measurement. Finally, positioning errors caused by residual stress were calculated.

guide positioning accuracy; residual stress; accuracy retentivity; finite element

2015-10-26

国家科技重大专项(2013ZX0400-1061)

TH16；TG251

10.3969/j.issn.1004-132X.2016.17.004

马文硕，男，1991年生。北京信息科技大学机电工程学院硕士研究生。主要研究方向为数字化集成设计。发表论文3篇。米洁，女，1971年生。北京信息科技大学机电工程学院教授、硕士研究生导师。杨庆东，男，1956年生。北京信息科技大学机电工程学院教授、硕士研究生导师。