深海重力活塞取样器取样系统波动力学建模与分析

文泽军　刘　湛,　金永平　田续玲　黄良沛

1.湖南科技大学机械设备健康维护湖南省重点实验室，湘潭,411201 2.湖南科技大学海洋矿产资源探采装备技术湖南省工程实验室，湘潭,411201 3.中南大学，长沙，410083



深海重力活塞取样器取样系统波动力学建模与分析

文泽军1刘湛1,2金永平3田续玲2黄良沛1

1.湖南科技大学机械设备健康维护湖南省重点实验室，湘潭,411201 2.湖南科技大学海洋矿产资源探采装备技术湖南省工程实验室，湘潭,411201 3.中南大学，长沙，410083

首先以深海重力活塞取样器为研究对象，深入分析重力活塞取样器的结构特点与冲击取样工作原理；同时考虑海底特殊的取样环境与底质特性，应用波动力学理论，构建重力活塞取样器取样系统波动力学模型。随后对取样系统进行离散化处理，依据该模型研究重力活塞取样器取样系统冲击取样过程的数值计算方法。最后以冲击取样效率与贯入深度为性能指标，分析取样器配重、冲击高度及取样管直径对重力活塞取样器冲击取样性能的影响，同时对冲击部件内部应力进行分析，研究结论对重力活塞取样器的设计与优化具有一定指导意义。

重力活塞取样器；海底底质；波动力学；数值模拟

0　引言

深海重力活塞取样器是在自重作用下冲击海底淤泥质与软土质底质进行取样的一种常用设备。其工作原理是利用重锤触发平衡杆，使夹缆释放装置在距海底表层一定高度时释放取样器，在重力作用下冲击并贯入海底底质中。在贯入过程中，取样管中活塞隔开静水压力形成负压抽吸底质，并减少样品扰动。取样结束，利用钢缆提拉活塞将整个重力活塞取样器提起，完成取样过程。

Skinner等[1]基于土力学对重力活塞取样器的贯入取样进行了分析与建模，并对管土相互作用、岩芯扰动等进行了详细研究。Xu等[2]从能量的角度对重力活塞取样器的贯入过程及贯入深度的影响因素进行了分析，并假设贯入阻力主要为管壁与底质间的摩擦力，建立了取样器贯入深度理论模型。Lunne等[3]对重力活塞取样器在取样时造成样品扰动的原因进行了分析，给出了相应设计准则以提高岩芯质量。在结构设计上，Renberg等[4]研制了一种带三脚架的活塞取样器，这种取样器可获取长达1 m且无扰动的底质。根据重力活塞取样器冲击取样的工作原理，对其冲击系统进行动力学分析尤为重要。文献[5-6]结合冲击机械系统工作原理，提出了撞击凿入系统的数值计算方法，并分析了冲击凿入效率的波动理论和凿入时应力波的能量。刘德顺等[7-8]提出了一种构造冲击机械系统波动力学模型的方法，并根据冲击机械系统力学模型中所包含的独立弹性杆的件数将冲击机械系统分为一元、二元和三元冲击系统。Lundberg等[9]给出了入射应力波通过接头后的透射波，分析了具有接头的冲击系统的能量传递效率。当前围绕重力活塞取样器进行的研究主要集中在应用静力学、运动学和刚体动力学去阐述其工作原理，或是集中分析岩芯应力变化及岩芯变形，而应用冲击系统动力学方法来分析重力活塞取样器冲击取样的研究未见报道。事实上，重力活塞取样器通过冲击海底底质进行取样，宜用冲击动力学方法将其作为冲击机械用冲击动力学方法进行研究。

本文应用波动力学理论，深入分析重力活塞取样器冲击取样系统动力学特性以及冲击参数对取样性能的影响规律，为重力活塞取样器的结构与冲击参数设计提供指导，从而实现冲击取样作业中对长岩芯、深层海底底质的获取，提高重力活塞取样器冲击取样性能。

1　取样器冲击系统波动力学建模

1.1冲击系统建模

分析重力活塞取样器结构特点及取样工作原理，将取样管、管接头、刀头抽象为既具有弹性又具有质量的弹性杆，如图1所示。基于波动力学理论，建立重力活塞取样器冲击取样为以弹性杆为基本元件的一元冲击系统波动力学模型。

图1　弹性杆单元

重力活塞取样器中，取样管轴向尺寸远大于横向尺寸，因此，在冲击取样时，忽略其横向运动，假定当应力波通过取样管时，取样管横截面仍保持为平面，截面上的应力分布是均匀的。即弹性杆中任一点的位移均满足一维波动方程：

(1)

式中，u为弹性杆中截面的位移；c为弹性杆材料的纵波波速，钢的纵波波速为5130m/s。

基于波动力学理论构建冲击取样系统波动力学模型时，将取样管抽象为弹性杆，整个冲击系统即为以弹性杆为基本元件的一元冲击系统，冲击工作介质海底底质，进行取样工作。

1.2工作介质建模

重力活塞取样器一般用于采取海底软泥，其工作介质(软泥黏土、砂质软泥黏土等)的动力学特性对整个冲击取样系统有着重要影响。主要表现如下：一方面因为冲击机械的作用是使工作介质变形与破坏，在工作端的位移以及对工作介质所做的功表征了冲击机械系统的性能与效率；另一方面，作为波动方程的边界条件，必须用它来求解冲击系统工作端位移以及冲击部件中的应力波。实际上，对于海底软泥黏土等弱弹性物质，可忽略其弹性影响，将工作介质简化为塑性模型。由于取样器不断贯入取样，底质将对取样器产生摩阻力，且在贯入过程中，取样器所受阻力主要为底质与取样管外壁间摩阻力。工作介质的贯入力与贯入深度关系曲线如图2所示。

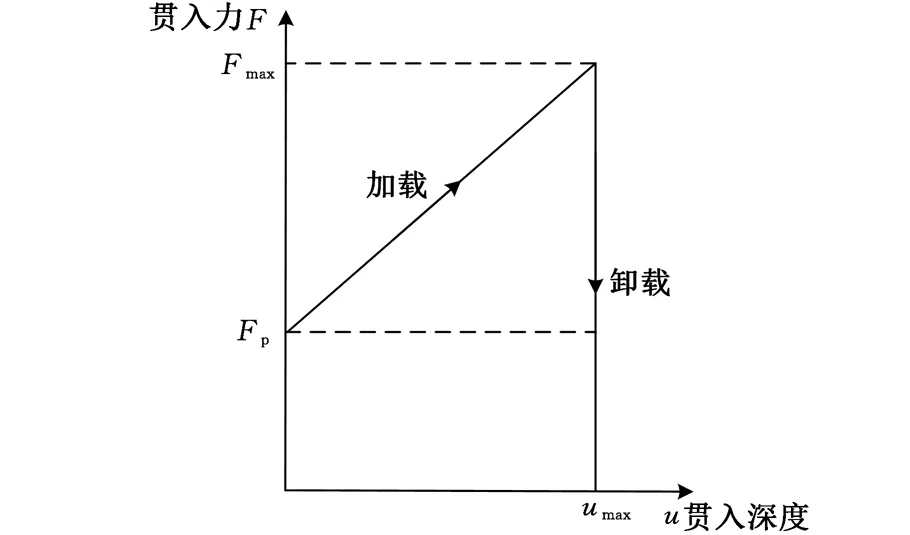
图2　工作介质贯入力与贯入深度关系曲线

考虑底质与取样管外壁间摩阻力，并假设其集中作用在取样管底端，海底底质力学模型可表示为

F=τglu+Fp

(2)

式中，F为贯入力；τ为海底底质极限应力摩擦系数(对于软泥黏土，τ取0.05～0.15kg/cm2)；l为取样管圆周长；Fp为海底底质的塑性极限阻力。

1.3取样器冲击取样性能

为了评估重力活塞取样器冲击取样系统的性能，定义冲击取样贯入深度为冲击系统工作端最大位移量umax；定义冲击取样效率η为冲击取样系统对工作介质所做的功和取样器初始动能与势能之和的比值，其标志着能量从冲击机械系统传递到工作介质中的效率，即

(3)

式中，mh为取样器质量；v0为取样器初始速度。

2　取样器冲击系统数值计算方法

2.1离散化

弹性杆中纵波波速为c，设时间步长为Δt，空间步长则为Δx=cΔt。将重力活塞取样器冲击系统中弹性杆沿轴向离散成若干等长度单元，使离散单元各界面与分段线相重合，并分别按顺序给分段线、界面编号，界面所在单元亦相应进行编号。图3为取样器冲击系统离散示意图。

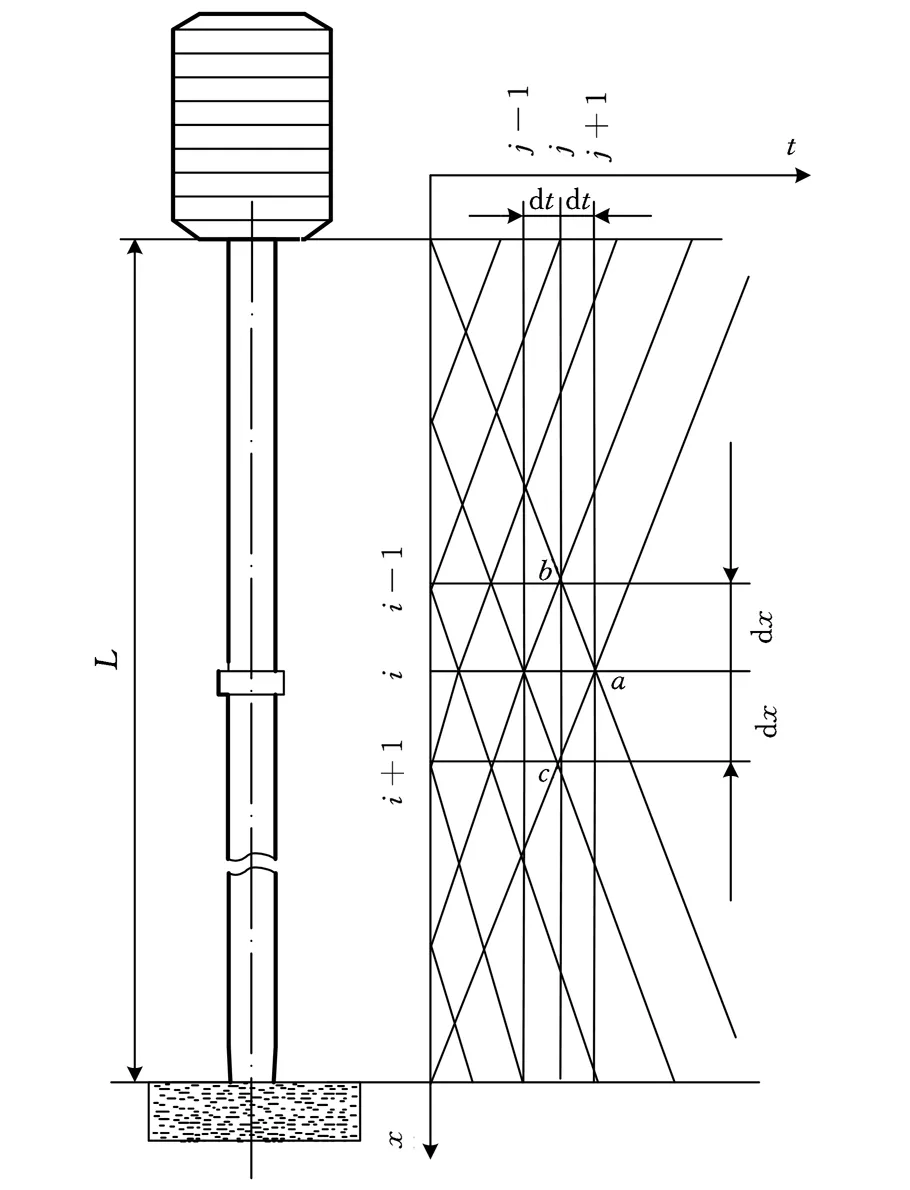
图3　冲击系统离散化

应用行波法求解波动方程时，假设在取样管各离散单元中同时存在相向而行的顺波与逆波，且单元界面上的合力及合速度与该界面上的顺波和逆波受力的关系为

(4)

其中，Pi,j、Qi,j、Fi,j、vi,j分别表示单元位置为i、计算步数为j时单元界面上的顺波受力、逆波受力、合力及合速度；Zi为取样管各离散单元的波阻。

2.2初始状态

重力活塞取样器在贯入取样前通过自由下落获得冲击初速度v0，考虑下落过程中海水浮力的影响，由能量定理得

(5)

式中，h为冲击高度；ρ为海水密度；u∞为势流速度；A为取样器最大截面积；CD为取样器阻力系数；f为取样器所受浮力。

根据等效撞击原理，取样管各离散单元中存在着初值分别为Pi,1、Qi,1的顺波与逆波：

(6)

2.3应力波传播

应力波在弹性杆中的传播包括两个方面：在弹性杆中匀截面部分的传播与变截面的传播，如图4所示。

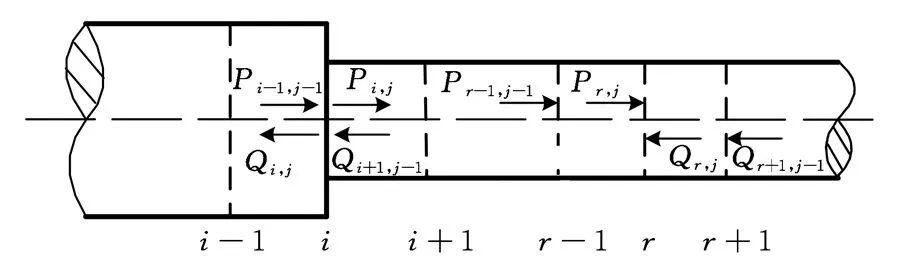
图4　应力波的传播

当应力波在匀截面部分中传播时，弹性杆中顺波、逆波有如下关系：

(7)

当应力波在变截面传播时，应力波将发生透射与反射。当应力波在弹性杆中从波阻为Zk的杆单元传播至波阻为Zk+1的杆单元时，其透射、反射系数分别为

(8)

式中，μ、λ 分别为透射系数与反射系数；Ak、Ak+1分别为截面位置为k和k+1处界面的截面积。

由透射和反射关系可得

(9)

因此，当应力波通过变截面时，变截面上所受的作用力与速度分别为

(10)

时，Pi,j、Qi,j表示通过变截面后形成的顺波与逆波受力；Pi-1,j-1、Qi+1,j-1分别表示到达变截面的顺波及逆波受力。

2.4取样管顶端

取样管在贯入取样过程中，顶部主要承受配重铅块等施加在取样管上的压力(重力)。因此，在冲击系统中，取样管的顶部端面始终受有一个压力的作用，假设配重质量为m，于是有

F1,j=G=mg

(11)

在样管顶部界面在F1,j的作用下，由应力波的传播关系得到离开样管顶部界面向取样管下端传播的顺波受力：

P1,j=F1,j-Q1,j

(12)

式中，Q1,j为到达样管端部界面的逆波受力。

2.5工作端

工作端即冲击取样系统冲击海底底质的界面，对其编号为N。在取样管冲击海底底质时，将会在取样管中产生沿轴线从工作界面向上传播的逆波，逆波在取样管顶端界面反射回来成为入射波传播至工作界面，时间为2L/c。到达工作界面的入射波在界面发生透反射，一部分入射波透射进入海底底质使其破坏，另一部分入射波在界面反射，继续在取样管中传播。在工作时，由撞击引起的应力波以及入射波在工作界面形成的反射波的形状与幅值取决于工作介质的性质。

根据工作介质的性质，贯入力FN,j与贯入深度uN,j的关系为

FN,j=τgluN,j+Fp

(13)

(14)

工作端界面的速度VN,j可通过下式求得：

(15)

(16)

因此

(17)

根据上一时刻的贯入力FN,j-1以及本时刻到达工作界面的入射波PN,j，可求得本时刻的反射波QN,j：

(18)

根据应力波叠加关系，利用工作界面的入射波PN,j以及求得的反射波QN,j，即可得到本时刻工作端的贯入力FN,j：

FN,j=PN,j+QN,j

(19)

在取样器冲击海底底质时，取样管中产生应力波，应力波在取样管中的传播使得取样管贯入海底底质进行取样。

3　取样器冲击系统主要技术参数的波动力学分析

重力活塞取样器在工作中，配套的取样管、管接头及刀头紧密连接，且均为钢制材料，在模型中将其视为整体。本文研究的重力活塞取样器取样管长度L为30 m，内径di为100 mm，外径d0为127 mm。在模拟重力活塞取样器冲击取样时，选取时间步长为20 μs，将冲击系统离散成N=300个单元。弹性杆材料纵波波速c=5130 m/s，密度ρ=7830 kg/m3；工作介质为淤泥质软黏土，将其作为塑性模型处理，考虑到贯入时底质与取样管间的摩擦力(取τ=0.08 kg/cm2)，为简便计，令X=EA/(3200Cd)，X为贯入时的无因次量。冲击速度v0=3.3 m/s，初始间隙设定为0。

3.1取样器配重的影响分析

重力活塞取样器的取样深度在一定程度上依靠于配重的设置。为了研究重力活塞取样器在不同配重下冲击取样时的动力学特性，当冲击高度h=1 m时，设置配重m为1400～2000 kg，得出取样器配重对于冲击取样性能的影响规律。

重力活塞取样器在不同配重m下的贯入深度如图5所示。由图5可知，随配重的增大，贯入深度增加6.25 m，配重为2000 kg时，贯入深度达到29.69 m，在此条件下，配重不需继续增加。这表明随着配重的增大，取样管顶部所受压力增大，提供的能量相应增加，因此，贯入深度随配重的增大而呈现显著增大的趋势。

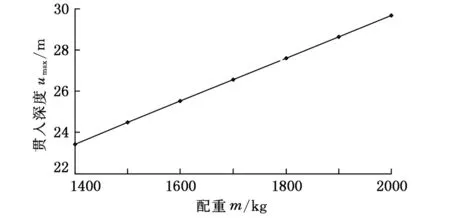
图5　配重对贯入深度的影响

分析不同配重m下的冲击取样效率可知，取样器冲击取样效率随配重的增大呈现缓慢上升的趋势。这是因为配重增大，取样器对海底底质做的功相应增大，冲击取样效率上升。不同配重m下的冲击取样效率如图6所示。

图6　配重对冲击取样效率的影响

3组不同配重下的最大应力分布见图7。图7a、图7b所示分别为各截面最大压、拉应力，其中横坐标0～300 mm为冲击系统离散截面位置，图中压应力符号为正，拉应力符号为负。模拟结果表明，随着配重的增加，取样管内部各个截面处最大压、拉应力均有所增大。由图7可看出，配重对取样管内部最大压应力的影响较之最大拉应力要大。分析可知，贯入力随配重的增加而增大，迫使取样管贯入底质中，因此，取样管内的入射应力波必然增大。同时，图7中出现4个应力突变处是因为在该位置存在管接头。

(a)最大压应力

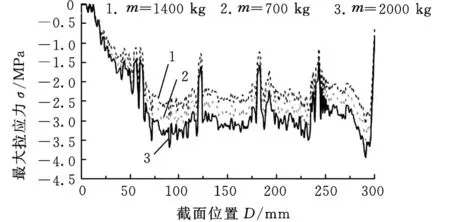
(b)最大拉应力图7　配重对取样管应力的影响

根据取样器配重变化对取样性能及取样管内部应力的影响分析，配重变化对取样管内应力的影响并不显著，而对贯入深度的影响较大，配重增大时，贯入深度及取样效率均增大，因此，可选取稍大配重。考虑到30 m重力活塞取样器最大贯入深度为30 m，因此，在此条件下配重选择2000 kg即可满足取样要求。

3.2冲击高度的影响分析

冲击高度影响取样器冲击海底底质的初始速度，当配重m为1800 kg时，设置6组冲击高度h，得出冲击高度对于冲击取样的影响。进行数值模拟时，刀头与沉积物做零间隙处理，根据式(5)将6组不同冲击高度换算为冲击初速度进行计算，见表1。

表1　不同冲击高度参数

冲击高度h为0.5～3.0 m时冲击取样的贯入深度如图8所示。从图8可知，冲击高度增大，贯入深度随之依次增大，这是由于取样器的能量来源于取样器自身重力做功，取样器的动能相对于重力势能较小，故通过增大冲击高度获得更大动能对贯入深度的影响也会相对较小。但在实际应用中，增大冲击高度对于增大贯入深度是有利的。

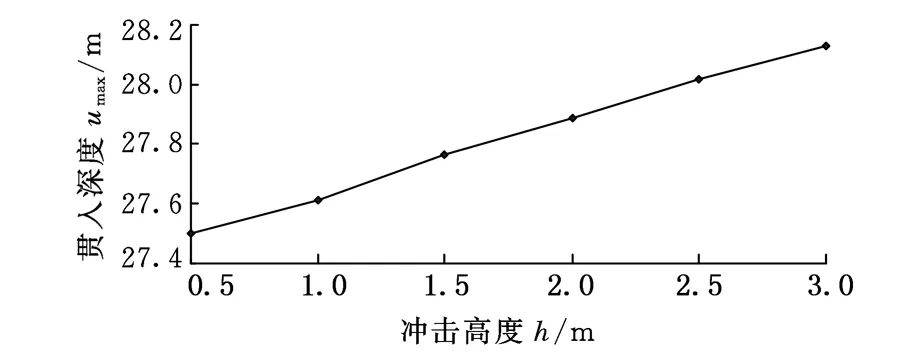
图8　冲击高度对贯入深度的影响

根据图9分析不同冲击高度h下的冲击取样效率可知，冲击取样效率随冲击高度的增大呈现下降趋势。出现这种现象是由于冲击高度增大时，海水阻力对取样器所做负功同样增大，加大了取样器能量的消耗，故出现取样效率下降的趋势。

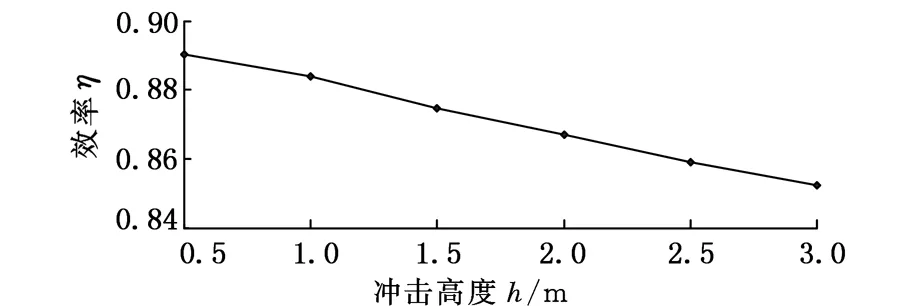
图9　冲击高度对冲击取样效率的影响

根据模拟结果可知，随着冲击高度增加，取样管内部各截面处最大压应力随之增大，而最大拉应力却随之减小，但影响均不明显。分析可知，冲击高度增大时，取样器重力势能增大，提供冲击取样能量相应增大。冲击高度增大对于取样管内应力影响较小，因此，从应力角度考虑，可增大冲击高度进行冲击取样工作。由于冲击高度的变化对取样管内应力几乎无影响，且冲击高度对冲击取样效率影响较小，而贯入深度随着冲击高度的增大而增加，故可通过增大冲击高度来提高重力活塞取样器的取样性能，满足取样要求。

3.3取样管直径的影响分析

在冲击取样系统波动力学模型中，设置配重m为1800 kg，冲击高度h为1 m，改变取样管外径d0，分析取样管直径对取样器性能的影响。

取样器在不同取样管直径下冲击取样的贯入深度如图10所示。由图10可知，随着取样管直径的增大，贯入深度下降5.33 m。这表明随着取样管直径增大，取样管所受摩阻力也增大，因此，贯入深度随着取样管直径增大而呈现显著下降趋势。

图10　取样管直径对贯入深度的影响

由图11分析不同取样管直径下的冲击取样效率可知，取样管直径的增大对取样效率的影响较小。取样效率随取样管直径的增大呈先增后减的趋势，取样管直径为131 mm时取样效率最大。这是因为当取样管直径较小时，贯入深度较大，因此刀头内壁与底质之间的摩擦阻力消耗的能量比贯入深度较小时多，而取样管直径较大时，由于端阻力的增大，也将产生额外的能量消耗。

图11　取样管直径对冲击取样效率的影响

模拟结果表明，随着取样管直径的增大，取样管内各截面处最大应力随之减小。其中3组不同取样管直径下的最大应力分布见图12。由图12可知，最大压应力出现于前端第一段取样管靠近管接头处，最大拉应力出现于取样管前端接近刀头部位。取样管前后端处出现应力集中现象，在管接头处，最大应力明显减小。分析可知，在截面积突变处最大压、拉应力都出现较大波动。由于前段两节取样管最大应力较高于其他部位，在实际工作中，重力活塞取样器冲击取样时取样管受到附加集中弯曲应力的作用，故可能引起取样管的弯曲失效。

(a)最大压应力

(b)最大拉应力图12　取样管直径对取样管应力的影响

根据对取样性能及取样管内部应力的影响分析，当取样管直径为125～140 mm时，钢制取样管满足冲击取样强度要求，冲击取样效率变化趋势不明显，而取样管直径越小，贯入深度越大。在此条件下，取样管直径不宜过大，可通过适当减小取样管直径来提高取样性能。

4　结语

(1)本文建立了以弹性杆为基本元件的重力活塞取样器冲击取样系统波动力学模型。基于透反射关系法，提出了重力活塞取样器冲击系统冲击取样的波动力学数值分析方法。

(2)应用重力活塞取样器冲击系统数值模拟程序，分析取样器结构参数与冲击参数对冲击取样性能的影响以及冲击系统中取样管内部应力的变化情况，为重力活塞取样器在结构参数与冲击参数的选择与设计提供指导。

(3)在取样器配重、冲击高度及取样管直径中，取样器配重与取样管直径对贯入深度及冲击部件内部应力影响较大，三者对冲击取样效率均影响较小。为提高重力活塞取样器取样性能，在实际设计应用中，应优先考虑取样器配重，其次考虑取样管直径，最后考虑冲击高度。

[1]Skinner L C, Mccave I N. Analysis and Modelling of Gravity-and Piston Coring Based on Soil Mechanics[J]. Marine Geology,2003,199(1/2):181-204.

[2]Xu Jian, Meng Guangyao. Analysis and Research on the Gravity Piston Corer Theory Based on ABAQUS[J]. Hydromechatronics Engineering,2013,41(24):87-92.

[3]Lunne T, Long M. Review of Long Seabed Samp-lers and Criteria for New Sampler Design[J].Marine Geology,2006,226(1/2):145-165.

[4]Renberg I, Hansson H. A Tripod Piston Corer for Taking a Meter-long Sediment Core with an Undisturbed Sediment-water Interface[J].Journal of Paleolimnology, 2011,46(2): 313-317.

[5]徐小荷. 撞击凿入系统的数值计算方法[J]. 岩石力学与工程学报,1983,3(1):75-83.

Xu Xiaohe. The Digital Calculation Method of Striking Penetration System[J]. Chinese Journal of Rock Mechanics and Engineering,1983,3(1):75-83.

[6]赵统武. 冲击凿入效率的波动理论研究[J]. 金属学报,1980,16(3):263-275.

Zhao Tongwu.A Study of the Efficiency of Percussive Penetration by Wave Theory[J]. Acta Metallurgica Sinica, 1980,16(3):263-275.

[7]刘德顺,李夕兵,朱萍玉，等. 冲击机械动力学与反演设计[M]. 北京:科学出版社,2007.

[8]刘德顺,李夕兵,杨襄壁. 冲击机械系统的波动力学研究[J]. 机械工程学报,1997,33(4):104-110.

Liu Deshun,Li Xibing,Yang Xiangbi.Wave Mechanics of Mechanical Impact System[J]. Chinese Journal of Mechanical Engineering,1997,33(4):104-110.

[9]Lundberg B, Okrouhlik M. Efficiency of a Percus-sive Rock Drilling Process with Consideration of Wave Energy Radiation into the Rock[J]. International Journal of Impact Engineering 2006,32(10):1573-1583.

(编辑陈勇)

Modeling and Analysis for Sampling System of Deep-sea Gravity Piston Sampler Based on Wave Mechanics

Wen Zejun1Liu Zhan1,2Jin Yongping3Tian Xuling2Huang Liangpei1

1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment,Hunan University of Science and Technology,Xiangtan，Hunan，411201 2.Hunan Provincial Engineering Laboratory of Equipment and Technology for Marine Mineral Resources Exploration,Hunan University of Science and Technology,Xiangtan, Hunan， 411201 3.Central South University, Changsha, 410083

The working principles and structure characteristics of gravity piston sampler were deeply analyzed herein, the mechanics characteristics of seabed sediments was considered, based on the theory of wave mechanics, the sampling system involving a single rod wave mechanics model was established. Then, the sampling system was carried out the discrete treatments, and the numerical calculation method of the impact sampling process of impact sampling system was researched. Finally, based on the numerical simulation program, the influences of sampler weight stand, impact height, and sampler pipe diameter on the impact sampling performance for gravity piston sampler were analysed, and the impact parts internal stress was also analyzed. The conclusions has important guiding significance to the design and optimization of gravity piston samplers.

gravity piston sampler; seabed sediment; wave mechanics; numerical simulation

2015-10-12

国家自然科学基金资助项目(51075141)

P756.5

10.3969/j.issn.1004-132X.2016.17.002