一种基于FPGA的RS编译码器设计与实现
2016-10-09张鹏泉曹晓冬范玉进褚孝鹏
张鹏泉,曹晓冬,范玉进,褚孝鹏,刘 博
(天津光电集团公司,300211)
一种基于FPGA的RS编译码器设计与实现
张鹏泉,曹晓冬,范玉进,褚孝鹏,刘博
(天津光电集团公司,300211)
RS码是线性分组码中具有很强纠错能力的多进制BCH码,其在纠正随机错误和突发错误方面非常有效,因此被广泛应用于通信和数据存储系统。本文提出了一种实现复杂度低、高效率的RS编译码器实现电路,包含RS编码器、Horner准则的伴随式计算、BM算法、Chien搜索等模块,以RS(15,9)为例运用VHDL在ISE14.6软件环境下进行了功能仿真,结果与Matlab得到的理论结果一致。该方法适用于任意长度的RS编码,有着重要的应用价值。
Reed-Solomon码;伽罗华域;BM算法;Chien搜索
0 引言
信号在传输过程中,可能会由于受到干扰或信道传输特性不理想等方面的原因导致信号发生错误,从而收到错误的信息,所以为了保障数字信号在传输过程中的可靠性,我们需要对原始信息进行信道编码。RS码由里得(Reed)和所罗门(Solomon)应用MS多项式于1960年构造出来,是一类具有很强纠错能力的编码,是二进制BCH码的多进制推广,建立在GF(q)(q>2,q属于正整数)有限域上,且RS码是MDS码,具有极大最小距离特性,它不仅可以纠正突发错误,还可以纠正随机错误,其卓越的纠错能力使得它在工程应用中引人注目,已被多个国际、国内标准采用。RS码主要应用于实时性较高的移动通信系统、深空通信、数字卫星电视、磁记录系统等方面。RS码已成为美国航天局(NASA)和欧洲空间局(ESA)在深空通信级联系统中采用的标准码。
1 RS编码原理及实现
在GF(qm)域中,m=1的q进制BCH码称为RS码,RS编码的表示形式为RS(n,k)。令α为GF(q)中的本原元,纠正t个错误的RS码的生成多项式g(X)以为其全部的根。由于是GF(q)中的元素,因此其最小多项式φi(X)即为X-。纠正t个错误的q进制RS码的生成多项式为:g( X)=LCM{φ1(X),φ2(X),…,φ2t(X )}将X-带入φi(X)得到:
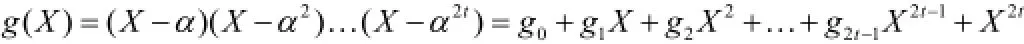
其中gi∈GF(q) 0≤i<2t 。由于是Xq-1-1的根,因此Xq-1-1能够被g(X)整除。所以g(X)将生成恰好具有2t个奇偶校验符号、长度为n=q-1的q进制循环码,且由BCH界可知,该码的最小距离至少为2t+1。以RS(15,9)为例,其编码参数如下:
码长n=15;信息位个数k=9;校验位:n-k =2t=6;纠错能力t=3;最小码距δ=2t +1=7;
本原多项式:p( X)=X4+X+1;

图 1 RS编码电路
码生成多项式:g( X)=X6+7X5+9X4+3X3+12X2+10X +12 RS编码的方法是令编码信息为:a( X)=a+a X+a X2+…+aXk-1其中k=n-2t,在系统码形式下,2t个奇偶校验符号恰是信息多项式X2ta( X )除以生成多项式得到的余式:b( X)=b+b X+b X2+…+bX2t-1的系数。在硬件实现中,这可以通过图1所示的除法电路来完成。
编码时,信息位分为两路送电路中,一路直接送入编码结果,一路送入除法电路并进行移位,k个时钟结束后,信息位全部输入,完成除法功能,此时移位寄存器中保留了余式b(x)的系数,即为校验位。再经过2t个时钟后数据全部移出,得到2t个校验位,接在k个信息位后,得到RS编码。
2 RS译码原理及实现
RS的时域译码可分为4步:1) 根据接收码多项式R(x)计算伴随式S(x);2) 用BM算法求解错误位置多项式σ(x)的系数;3) 用Chien搜索算法求错误位置多项式σ(x)的根;4) 计算错误值与错误位置并进行纠错。迭代译码的关键在于运用BM算法和Chien搜索电路加快求解σ(x),下面将详细介绍。
2.1伴随式计算模块
式中b0=0表示初始化时所有寄存器置0。图2位计算伴随式系数的实现电路,15个时钟周期后可接收完所有15个符号,同时得到全部6个伴随式系数。
2.2BM迭代算法
2.3Chien搜索算法
在RS码的译码过程中,求σ(X)的根的目的是判断码元出错的位置,Chien搜索实际上是一种试探性穷举的计算方法,逐个试探各个码元位置是否有错。对于(n,k)RS码,要判断第i位是否出错,相当于要确定是否是错误未知数,即检验α-i是不是错误位置多项式σ(X)的根。若σ( α-i)=0或,则第i位为错误位置,在译码过程中,依次检查α-i是否是错误位置多项式σ(X )的根就是Chien搜索过程。Chien搜索可以用图3所示电路结构实现。
从缓存中读取第一个码元Rn-1前,t个乘法器执行乘法运算后移位,且保存σiαi,并送入求和判断模块,若和为-1,则判断模块输出,从接受码元中减去相应的错误值yn-1,实现对该码元的纠错译码。在译完第一个码元Rn-1后,再进行乘法运算,存储σiαi,然后由求和判断模块决定输出。依此类推,直到最后一个码元R0的译码。
综上所述,RS码的BM-Chien译码器的结构设计如图4所示。
3 仿真结果
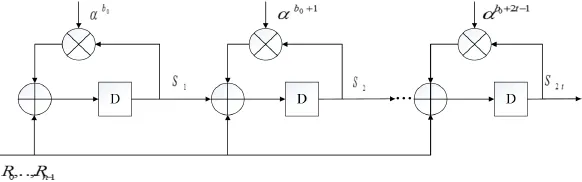
图 2 RS伴随式计算电路

图 3 Chien搜索电路
RS(15,9)编解码器及所有模块均在Xilinx公司的ISE14.6开发环境中成功调试和综合下载,器件选用Xilinx公司Spartan6系列中的XC6SLX9,仿真工具采用ISIM。编解码系统仿真中的输入输出均为流水线工作模式,在译码仿真中已加入误码测试纠错能力,仿真结果如图5图6所示。
编码前的数据由高位到地位送入din端口,im是输入有效信号,oe是输出有效信号,从im置1的第n个时钟后编码完成,得到结果与Matlab仿真结果对比,完全一致,证明编码正确。
在输入有效后的第n+4t+7个时钟后开始输出译码结果,en为输出有效信号,译码之后的输出数据dout与din相同,且能够纠正之前加入的误码。
4 总结
RS编码的所有运算都是建立在有限域v的基础上的,其中除法电路的设计、BM迭代算法和Chien搜索是核心模块。本文实现了以(15,9)为例的RS编解码设计与仿真,仿真的输出结果与理论分析一致,且基于相同原理,本方法可实现任意长度的RS编解码设计。
[1] 曹雪虹,张宗橙. 信息论与编码[M]. 清华大学出版社,2005.
[2] ShuLin Jr,何元智. 差错控制编码[M]. 机械工业出版社,2007.
[3] 张宗橙. 纠错编码原理和应用[M]. 电子工业出版社,2005.
[4] 刘东华,向良军. 信道编码与Matlab仿真[M]. 电子工业出版社,2014.
Design and implementation of a RS encoder and decoder based on FPGA
Zhang Pengquan,Cao Xiaodong,Fan Yujin,Zhu Xiaopeng,Liu Bo
(Tianjin photoelectric group company 300211)
RS code is a linear block code with a strong error correction ability of the multi band BCH code,which is very effective in correcting random errors and burst errors,so it is widely used in communication and data storage systems. In this paper, the results are consistent with a theory to achieve low complexity and high efficiency of the RS compiled code realization circuit,with computing,BM algorithm,Chien search module that contains a RS encoder, Horner criteria,to RS (15,9) as an example using VHDL in ISE14.6 software under the environment of the function simulation,the results with MATLAB software.This method can be applied to any length RS code, and it has important application value.
Reed-Solomon code; Galois field; BM algorithm;Chien search

图 4 RS码译码器硬件结构图

图5 RS编码仿真结果

图 6 RS译码仿真结果
